基于群签名的电子投票方案
乔汇东,胡 瑛
(湖南工程学院 计算机与通信学院,湘潭411104)
1 电子投票基本要求
通常认为,一个安全的电子选举方案应该满足如下七个方面的安全性.①完整性,即所有有效的选票都应当被正确统计;②坚固性,即无人能破坏选举,合法选民可以退出投票而不会影响到投票的正常进行;③匿名性,即任何人都不能将选票与该选票的投票者对应起来;④唯一性 只有合法的投票者可以投一次票;⑤合法性,即有选举权的投票人才能参加选举的;⑥公正性,即无人能知道选举的中间结果;⑦可验证性,即投票人可以验证自己的选票被统计到最后结果中.
电子投票发展至今,一些新的要求也出现在电子投票方案中,主要包括:①稳固性,投票系统可以对一些局部错误进行容错;②广泛的可验证性,所有人都可自行验证投票是否公平进行;③无收据性,投票人不能向其他人证明自己投票的内容.其中,无收据性的概念主要用于防范“选票收买”和“强迫投票”的违规行为,而这两者是选举舞弊的常见手段,因而,无收据性方面的研究得到了重视.
2 电子投票方案研究现状
目前,主要电子投票系统有:基于同态加密的投票系统、基于匿名信道和盲签名的投票系统、基于Mix-net的投票系统或者是基于秘密分享和安全多方计算的投票系统.众多电子投票方案中,Fujioka[1]等人提出的,基于盲签名的投票系统被普遍认为是一个高效实用,最有代表性,且适合大群体选举的电子投票方案,后续很多方案都借鉴了其中的一些方法,虽然这种投票机制一直被视为最具实用价值的,然而,后来的研究显示它仍存在一些突出的缺点:验证机构权力过大;投票者在验证机构注册之后如果放弃投票将会造成混乱;合法的选票之间可能会有重复;没有投票人的协助无法打开选票.为了解决这些问题,赖瑾[2]等提出:设置发放唯一选票序列号的发放中心,以保证选票不发生碰撞;在验证机构设置多个验证者,以门限多重签名的方式受理投票者的注册请求来防范验证机构可能存在的舞弊行为;设置监票人监督计票工作;允许最终投票的人数少于前去注册登记的人数,权利机关此时有权补上这个差异以此解决中途弃权的问题.冯泽涛[3]的方案则以多重验证、可验证的投票编号等技术来解决签证人欺诈和选票碰撞问题.而陈晓峰[4]等则在他们的方案里采用时限比特承诺解决了没有投票人的协助无法打开选票的问题.总的来说,对于管理者的信任仍是这些投票方案的安全基础,而这一点对于很多选举来说显然并不合适,另外,大部分此类方案中无收据性也没有得到实现.无收据性的概念由Benaloh[5]提出,利用高度剩余加密技术,他在其论文中首次给出了基于特定物理假设voting booth的无收据投票方案,但Martin[6]随后证明了在多个计票机构情况下,其方案不满足无收据性.Lee[7]则提出了用“可信赖第三方”来实现无收据,其投票方案基于同态加密实现,但这种完全的信任被陈晓峰[8]等认为是不合适的,后者同样使用同态加密提出了一个较为完备的基于半信任模型的无收据投票系统,然而,其方案中管理机构和投票者之间的交互比较频繁,方案步骤一定程度上取决于候选人的数量,如果候选人较多,则每个投票者都需要和管理机构进行多次交互才能完成选票的产生,这些情况使得该方案在大群体选举中并不合适.无收据性从逻辑上来说也常常和可验证性等问题的解决有一定的冲突,无收据要求不能证明选票内容,而可验证要求能验证投票结果,这使得两者常不可兼得,比如在一些基于同态和门限签名的方案中,实现了无收据,然而却无法防止计票机构的舞弊行为,因为投票者无法监督具体到自己的每一票的开票结果,而无收据性问题的要求非常高,目前大部分方案实现仍然是困难的.
随着研究的发展,一些新的方案中,也开始以群签名和环签名来构造投票系统,如陈晓峰[4]等提出的方案使用了群签名和知识签名,崔国华[9]等则利用了群签名的推广列表签名,而宋春来[10]提出的方案使用了环签名.群签名和环签名由于其本身的匿名性为电子投票带来了主要便利,而链式环签名同时还解决了唯一性问题,保证了投票者无法多投选票.但环签名方案效率偏低,每次签名产生与签名验证过程需要使用该环中所有成员的公钥逐一进行运算,如果成员较多,其运算量很大,若成员太少又有可能容易暴露投票者的信息,通常要以之实现大群体的投票是困难的.由于一个完备的群签名通常具备匿名、不可伪造、不可关联、抗联合攻击、可跟踪等特性,使得群签名方案比较适合用来作为构造电子投票系统的基础.以知识签名构造的群签名方案通常在实现群签名的各项性能上表现良好,其研究也十分活跃,在这些方案中选择的合适方案做为构造电子投票系统的基础更为可行.
3 准备工作
3.1 知识签名
知识签名由Camenisch[11]提出,并在后续的研究中逐步完善,主要知识签名形式有:
定义:满足等式c=H(m‖y‖g‖gsyc)的数组(c,s),即为关于消息m的y以g为底的离散对数的知识签名,表示为:SPK{α:y=gα}(m),其中希腊字母α表示签名者持有的秘密,符号||表示二进制串连接符,H 表示安全Hash函数H:{0,1}*→{0,1}k.
这样一个知识签名(c,s)只有在知道秘密x=loggy的情况下才能生成,当知道x的值时,签名者随机选取r∈Z*n,然后进行计算:c=H(m)‖y‖g‖gr),s=r-cx mod n ,就可以得到签名(c,s),能生成这样一个签名说明了签名者知道y以g为底的离散对数x,不知道x的情况下任何人想伪造一个签名都必须能够解决离散对数问题,所以这样一个知识签名可以证明y是由某个以g为底的离散对数x生成的gx,并且签名者知道关于y=gx的秘密值x.在文献[11]中Camenisch还给出了其他知识签名,包括:
关于消息m的y以g,h为底的离散对数的知识签名:
SPK{(α,β):y=gahβ}(m),(α,β)表示签名发出者所持有的秘密;
关于消息m的y以g为底和z以h为底的离散对数的知识签名:
SKREP[α:y=gg∧z=hα](m);
关于消息m的y以g为底的离散对数的e次方根的知识签名:
SKROOTLOG[α:y=gαe](m);
关于消息m的且v有着形式v=hαgβe的知识签名:
E-SKROOTREP[(α,β):v=hαgβe](m).
3.2 基于知识签名的群签名方案
基于知识签名方案中,比较著名的有CS97和ACJT[12]等经典方案,很多其方案也是以它们为基础进行改进得到的,CS97群签名方案由Camenisch在文献[11]中提出,其基本步骤如下:
(1)系统建立
群管理员计算下列值:
①一个RSA模n及两个公开的指数e1,e2>1,其中e2与φ(n)互素,e1,e2应较小.
②两个整数f1,f2>1,并且在不知n的因子分解时计算其e1次根及e2次根是困难的.
③阶为n的循环群G=〈g〉,使得在G中计算离散对数是困难的.
④一个参数h∈G,使得计算h关于g的离散对数是困难的.
⑤选取一个随机数ρ∈Z*n,计算yR=hρ作为群管理员的公开密钥.群组的公开密钥Y=(n,e1,e2,f1,f2,G,g,h,yR),保留ρ和n 的素因子作为群管理员的秘密私钥.
(2)成员加入
要注册成为一个成员,Alice首先计算她的成员密钥:
y=xe1mod n其中x随机选取自,z=gy公开z作为Alice的公钥
为了防止群管理者知道秘密y,Alice需要采用盲签名的方法来发送她的加入请求,Alice计算:
U = E-SKROOTLOG[α:z=gαe1](‘’)
V=E-SKROOTLOG[β:g~y=(zf1gf2)βe2](‘’),‘’表示空字符
(3)签名
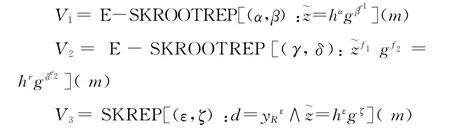
(4)验证
验证者只要验证3个知识签名V1,V2,V3通过就可以认为签名,d,V1,V2,V3)是一个合法的群签名.签名V1,V2说明了签名者有能力给出等式mod n=(f1βe1+f2)mod n,从而验证了签名者的身份,签名V3保证了这个签名是可以被群管理者打开的,所以当3个知识签名都验证通过,这个群签名为有效.
(5)打开签名
因为签名V3证明了d=yRε和=hεgζ,所以群管理者可以计算:z=/d1/ρ恢复出签名者使用的公钥z,找到签名者,并且用知识签名SKREP[α:h=yRα∧=zdα](‘’)在不泄露ρ的情况下向他人证明.
4 新的电子投票方案
4.1 系统参与者说明
(1)投票群G,一个由有权参加投票的人构成的群;
(2)群中成员Vi,i=1,2,…;
(3)群管理机构GM,负责建立群,接收合法成员的加入请求,并给合法的选票予以注册;
(4)计票机构C,负责解开选票、统计选举结果.
4.2 系统准备
(1)系统初始化阶段
系统初始化阶段由GM以群管理者的角色完成群的建立和成员加入步骤,基本步骤按照CS97群签名方案完成.只是在成员加入时,需要GM进行身份的审核,确保拥有投票资格的合法成员才能加入群内.成员加入完成后,GM将加入成员名单发布到电子公告牌,如无异议则进入下一阶段.
(2)注册阶段
此阶段各成员将构造自己的选票,并向GM和计票中心C注册选票.在此次投票的注册开始时,GM将首先产生选取自的随机数rGM,并秘密保存.
投票者Vi构造选票,Vi首先确定其选择的结果resulti,这应是一个说明Vi最终投票结果的信息,接着Vi应对resulti添加不定数量的冗余信息,如时间,地址,或其他任何随机添加的各种冗余信息,形成vi,但要保证resulti仍能从vi中被正确的识别出来.这个过程我们这里描述为算法diverse(result,r1,r2,r3,…,rn),其特点是无论参数result或ri,i=1,2,…,n,n,哪个发生变化,都将使d=diverse(result,r1,r2,r3,…,rn)计算得到的d 不同,然而,如果使用算法result=conclude(d)进行逆向处理,总是能够得到原参数中的第一个参数result,即:

此时,Vi利 用 算 法diverse(resulti,r1,r2,r3,…,rn)得到vi,并秘密保存.这里的ri,i=1,2,…,n指代各种冗余信息的加入,这一构造选票的过程是为了确保这样一个事实:即使Vi投票的结果resulti已知,其他人仍无法推断出Vi所使用的选票vi,因为其他人无法知道vi形成过程中使用了哪些ri参数,而算法conclude又保证任何人在需要的时候可以检验选票vi中包含的投票结果是否为resulti.另外,Vi需要对自己的选票vi负责,如果形成无法conclude或错误conclude的结果,他的选票将作废或被错记.然后Vi计算得到待注册的选票信息mi=H(vi)Rie1mod n,其中Ri为取自Z*n的随机数.接着,Vi对mi进行群签名,得到Sig(mi)后发送分组(mi,Sig(mi)Vi)给 GM.
GM验证签名,验证失败则拒绝此分组,应用签名打开步骤计算此成员的公钥,以判断此成员之前有无发出过注册选票,如没有则补充证据si,即产生知识签名si=SKREP[α:h=yRα∧~z=zdα](mi),接收注册选票并保存分组(mi,Sig(mi)vi,si),并将此签名的公钥zi发往电子公告牌.
GM对mi进行下面的计算:wi=mod n,ti=gwi,ci=wirGMmod n,并产生知识签名:sli=ESKROOTREP[α:gmi =gαe1∧ti=gα](‘’),s2i=SPK{β:gci=tiβ}(‘’)和s3i=SPK{β:gci-1=ti-1β∧gci=tiβ}(‘’),ci-1,ti-1指的是 GM 计算给上一位投票者的同类参数,可以在电子公告牌上查询.然后将(ci,ti)发送给电子公告牌并入对应的签名一栏.接着 GM 发送分组(ci,ti,s1i,s2i,s3i)给Vi.
Vi收到分组(ci,ti,s1i,s2i,s3i)后,验证知识签名s1i,s2i,s3i确 认ci是否为:ci=md1irGMmod n的形式,以及参数rGM是否和上一位投票者相同,验证失败Vi将公布(ci,ti,s1i,s2i,s3i)进行抗议,并要求重新注册.若验证通过,则计算:votei=ciR-1i,秘密保存注册选票votei.
(3)投票阶段
计票中心C宣布投票开始后,GM把rGM秘密发送给C,投票者Vi将自己的选票(vi,votei)通过匿名信道秘密提交给C,C执行验证:svotei=voteir-1GMmod n,(svotei)e1如果和 H(vi)相等,则通过验证,否则拒绝选票.对于通过验证的选票vi,C计算resulti=conclude(vi),把resulti结果统计到选票当中,并把(svotei,vi,resulti),同时发送到电子公告牌,如投票者Vi发现自己的选票vi没有出现在电子公告牌上,将提出抗议.当投票时间截止后,计票中心C宣布最后的统计结果.
5 安全性分析
合法性:群成员都是经过身份核实而加入群中的,群外的非法攻击者无法产生有效的群签名,从而杜绝了外部攻击,而群内部,即使是群管理者GM也无法模仿某个群成员发出签名.
完整性:每一张合法的选票都会被群中心C计入.由于使用了diverse算法,即使投票者们选择的结果resulti相同,但他们的选票vi也不会相同,所以vi的差别性保证了任何人都可以通过查看电子公告牌上的选票记录确定自己的票是否被统计,从而使得C无法隐匿选票.
可验证性:一方面投票者能通过电子公告牌查看自己的选票,另一方面其他任何人也可以通过(svotei,vi,resulti)校验选票的最终合法性,公告的最终统计结果能接受所有人的检验.
公平性:在选举过程中,由于选票始终处于盲化因子Ri和rGM的保护下,使得选票情况无法解读,即使GM也无法获知选举情况.
坚固性:使用电子公告牌公示群成员后,GM在投票开始前无法虚构成员加入群,注册阶段,由于签名打开部分的验证功能,所以不知道其他成员的密钥情况下,任何人包括GM也无法冒充其他人签名.注册过程中GM向投票者发放的知识签名证明了GM注册选票行为的规范,避免了GM故意破坏选举的可能,同时由于每张注册选票的rGM都相同,也避免了在开票阶段,GM利用特殊盲化因子影响选举的可能.
匿名性:由于使用了盲化因子和匿名信道,在最后解开选票后,即使是计票中心和群管理者联合起来,也无法从选票本身联系到投票者的身份.GM虽然可以在注册阶段跟踪投票者,却无法将最终选票和注册选票联系到一起,从而实现了投票者的匿名性.
唯一性:利用群方案中打开签名的操作,GM可以识别成员有否反复投票,重复或多投的票都将被拒绝.
无收据性:投票者无法向别人证实电子公告牌上最终选票中哪张是自己的,同时,在注册阶段后他所持有的待提交的选票votei,其内容也包含盲化因子rGM,因此他也无法向其他人证明votei中的内容.但此方案无法避免强迫投票,并且如果候选人和GM勾结,那候选人也可以令投票者证实其votei中的投票内容从而达成选票的买卖.
6 结 论
本文在群签名的基础上提出了一个利用知识签名、盲签名和匿名信道构造的一个较为安全的投票系统,系统具备大部分传统方案的优势,也考虑了无收据性等较强的要求,实现了一个较为可靠的电子投票方案.
[1] Fujioka A ,Okamoto T,Ohta K.A Practical Secret Voting Scheme for Lage Scale Elections[C].AUSCRYPT'92.LNCS 718,Berlin,Springer-verlag,1993:244-251.
[2] 赖 瑾,范玉顺.一种新的安全、实用的电子投票方案[J].计算机科学,2003,30(1):142-144.
[3] 冯泽涛.一个改进的匿名电子投票方案[J].计算机安全,2007,(4):38-41.
[4] 陈晓峰,王育民.基于匿名通讯信道的安全电子投票方案[J].电子学报,2003,31(3):390-393.
[5] Benaloh J,Tuinstra D.Receipt-free Secret-ballot Ellections[C].In Proceeding of the 26th Symposium on The Theory of Computing(STOC'94),Montreal,1994:544-553.
[6] Martin H,Sako K.Efficient Receipt-free Voting Based on Homomorphic Encryption[C].EURO-CRYPT'00.LNCS 921,Berlin,Springer-verlag,2000:393-403.
[7] Lee B,Kim K.Receipt-free Electronic Voting through Collaboration of Voter and Honest Verifier[C].In:Proceeding of JWISC2000,Okinawa,Japan,2000:101-108.
[8] 陈晓峰,王继林,王育民.基于半信任模型的无收据的电子投票[J].计算机学报,2003,26(5):557-562.
[9] 崔国华,汪 洋,粟 栗.基于列表签名的安全电子投票方案[J].计算机工程与科学,2008,30(1):4-7.
[10]宋春来,殷新春,孟纯煜.基于环签名的安全电子投票方案[J].计算机应用与软件,2008,25(5):29-30.
[11] J.Camenisch.Efficient and Generalized Group Signatures[C].In:W.Fumy,eds.Advances in Cryptology-EUROCRYPT'97,LNCS 1233,Springer-Verlag,1997:465-479.
[12] G.Ateniese,J.Camenisch,M.Joye,G.Tsudik.A Practical and Provably Secure Coalition-resistant Group Signature Scheme[C].In:Advances in Cryptology-CRYPTO'00,LNCS 1880,Springer-verlag,2000:255-270.

