基于灰色理论的市政排水工程造价估算方法

刘翠翠 段晓辉

(1.西安市政设计研究院有限公司，陕西西安 710068; 2.西安中铁一局电务处，陕西西安 710054)

0 引言

目前对于排水工程，一般是以相似已建工程的造价资料为基础，采用类比、回归分析等近似估计的方法，估算拟建工程的造价。然而，由于市政排水工程存在着干扰因素多、设计周期短、任务重、建设工期短等特点，所以本文在分析市政排水工程特征的基础上，用灰色理论估算模型对排水工程进行造价估算分析。

1 灰色理论和步骤

1.1 灰色理论原理

由于市政排水工程本身具有单一性、复杂多样等特点，因此不存在两个完全一样的工程。但存在着差异较小、较相似的一些工程，这种相似性构成了灰色理论估价的基础。将需要估价的市政工程称为拟估工程，已知造价的已建工程称为已估工程。利用与拟估工程最相似的几个已估工程的造价作为原始资料，采用指数平滑法，对拟估工程的造价进行预测[2]。

1.2 灰色理论估算计算步骤

1.2.1 工程特征参数及其影响权重的确定

将影响工程造价的主要因素集中起来，组成一个工程特征参数序列，代表该工程。在工程特征参数中选取复杂的、费用较大的因素为基准因素，其工程特征参数系数为1，其他各因素分别与该因素相比较，在闭区间[0，1]上结合具体情况赋予工程特征参数系数。由于各工程特征参数对工程造价的影响程度不同，因此在估测时赋予不同权重，以提高估算的精度;原则是越费时、费钱的，其权重越大，反之，则越小。

1.2.2 关联度的计算

1)设有m个已估工程A1，A2，Λ，Am，每个已估工程有n个工程特征参数:

T={t1，t2，Λ，tn}。

令第i个已估工程的工程特征参数为子序列，记为:

Xi={Xi(t1)，Xi(t2)，Λ，Xi(tn)}，i=1，2，Λ，m。

拟估工程为A0，X0，拟估工程的工程特征参数为母序列:

X0={X0(t1)，X0(t2)，Λ，X0(tn)}。

2)原始数据变换。

原始序列不具有可比性，必须要消除量纲，转换为可比较的序列。因此，必须对数列进行规范化处理。在本文中采用的是初值化，初值化是指所有数据均用第一个数据去除，然后得到一个新的数列，这个新的数列即是各个不同时刻的值相对于第一个时刻的值的百分比。

3)求绝对差序列。

绝对差值是指参考序列与比较序列的绝对差值:

根据式(1)可得出Δmin和Δmax分别为绝对差值的最小值和最大值。其中:

4)计算关联系数。

经数据变换后，参考序列变为{x0(k)}，比较序列变为{xi(k)}。灰关联系数表示各时刻数据间的灰关联程度，在k时刻序列{y0(k)}与序列{yi(k)}的灰关联系数为L0i(k)。

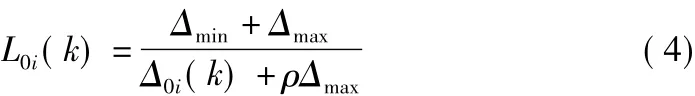
Δmax和Δmin由式(2)和式(3)得出，分别为所有比较序列各个时刻绝对差中的最大值与最小值。因为比较序列相交，所以一般取Δmin=0;ρ为分辨系数[3]，通常设定为0.5。关联系数的范围为0≤L≤1。

5)计算关联度。

令工程特征参数{t1，t2，Λ，tn}的影响权重为 {w1，w2，Λ，wn}，，权重指的是工程的各个特征参数对造价的影响程度，主要是根据专家咨询或经验来确定，设关联度为γ0i。

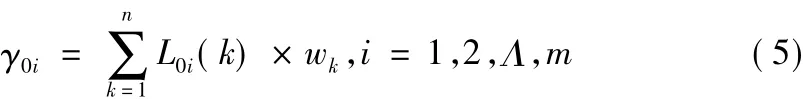
其中，γ0i为比较序列yi(k)与参考序列y0(k)的关联度;n为数据个数。关联度越大，说明已估工程与拟估工程的相似程度越大。最终按具体情况选取几个关联度大的已估工程。

6)把关联度 γ0i按从大到小排序，记为 γ01，γ02，Λ，γ0m，对应的单位造价为c1，c2，Λ，cm。选取关联度最大的3个已估工程，关联度为 γ01，γ02，γ03，对应的单位造价为 c1，c2，c3。待估工程 A0的单位工程造价C0的估测模型为:

1.2.3 拟估工程计算结果可靠性检验

将拟估工程作为已估工程，重复上述步骤对各已估工程进行估价，若计算结果与已知造价误差小于10%，则满足精度要求，说明关联系数取值合理，估测结果可靠;相反则另选已估工程。

2 排水工程特征分析及估算

市政排水工程中，影响工程造价的主要特征因素包括雨污水管道平均管径、雨污水管道长度、雨污水管道埋深及开挖坡度、雨污水管道基础类型、雨污水检查井平均井径及平均井深、雨水口类型等。这些特征因素有些具有相对独立性，有些是相互关联的，比如管道埋深与检查井的井深有很大的相关性，只需要选择其中一个。因此，最后确定下来的工程特征因素都是相互独立的。

从定量的角度分析确定的因素主要有:相应道路的长度(S1)，雨污水管道长度(S2，S3)，雨污水管道平均管径(S4，S5)，雨污水管道平均埋深(S6，S7)，雨污水检查井平均井径(S8，S9)。其中长度、埋深的单位为m，管径、井径的单位为mm，造价C的单位为万元/延米。

现列举9个实例样本，前面8个样本是已估工程，第9个样本是待估工程。这些样本的工程特征及造价见表1，根据样本工程赋予的工程特征参数系数及权重见表2，表3。

表1 工程特征及造价样本数据库

表2 排水工程参数系数

表3 每个影响因素对应的权重 %

在这9个样本工程中，选取5个样本工程作为已估工程来估算拟估工程。根据灰色理论原理，利用计算机程序筛选的5个已估工程中，将任意一个已估工程当作预估工程，轮流计算各已估工程自身的单位估价，看是否满足精度要求。在本例中，最终选取误差较小的第2个、第3个、第5个、第7个、第8个共5个样本工程作为已估工程。

其计算步骤如下:

1)为方便起见，先对这5个已估工程进行排序，重新编为子序列 X1，X2，X3，X4，X5，第 9 个作为拟估工程(母序列 X0)。然后对这些序列的参数系数进行初值化。

2)利用式(1)，计算各子序列Xi与母序列X0在第k点的序列差为Δ0i(k)。

Δ01=(0，0.167，0.125，0.08，0.125，0.06，0.158，0，0)。

Δ02=(0.091，0.333，0.625，0.083，0.063，0.118，0，0.059，0.056)。

Δ03=(0.182，0，0.125，0，0.125，0.059，0.053，0.176，0)。

Δ04=(0.091，0.167，0.625，0.083，0.06，0.059，0.105，0.059，0.06)。

Δ05=(0.545，0.333，0.375，0.25，0.063，0.235，0.211，0，0)。

3)利用式(2)及式(3)，计算两级最小差和两级最大差。

4)利用式(4)，计算关联系数L0i(k)。

L01=(1，1，0.652，0.538，1.00，0.714，0.839，0.664，1，1);

L02=(1，0.484，0.333，0.789，0.833，0.726，1，0.842，0.849);

L03=(0.632，1，0.714，1，0.714，0.842，0.856，0.639，1);

L04=(0.775，0.652，0.333，1，1，0.842，0.748，0.842，1)。

L05=(0.364，0.484，0.368，0.538，0.7，0.57，0.597，1，1)。

5)利用式(5)，计算关联度γ0i。

γ01=0.839，γ02=0.764，γ03=0.827，γ04=0.826，γ05=0.661。

6)利用式(6)，计算拟估工程的造价。

在计算出来的关联度中选取最大的三个关联度，按从大到小的顺序排列为γ01，γ03，γ04，对应的3个已估工程分别为第2个、第5个、第7个，则:

C0=(0.839 ×0.066 6+0.827 ×0.086 1+0.826 ×0.084 7)/(0.839+0.827+0.826)=0.079 1。

利用灰色理论模型估算出的第9个拟估工程的造价为0.079 1万元，其实际造价为0.075 8万元，相对误差为(0.079 1－0.075 8)/0.075 8=4.29%，在允许误差范围 ±10%以内，符合精度要求。

3 结语

在分析市政工程中的排水工程特征的基础上构建灰色理论模型，从定量和定性角度对排水管道工程的造价进行了估算，克服了传统的估算方法的缺陷，为市政工程造价估算提供了简捷而有效的方法。

[1] 邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社，1990.

[2] 郭 琦.工程造价管理理论与方法[M].北京:中国电力出版社，2004.

[3] 刘思峰，郭天榜.灰色系统理论及其应用[M].开封:河南大学出版社，1991.