一种基于形状矩阵的傅里叶描述子

张瑜慧

(宿迁学院三系，江苏 宿迁 223800)

责任编辑:魏雨博

图像检索是多媒体技术与数字图像处理领域的一个研究热点。描述图像内容的视觉特征一般有颜色、纹理、形状和空间关系等。形状是人们对图像理解的重要内容之一，现有的形状描述算法一般分为基于目标轮廓的形状描述子和基于区域的形状描述子两大类［1－2］。

一个好的形状描述子应具备对平移、缩放和旋转的不变性，同时应具有紧致性和计算的简单性，当然还应具有较强的形状区分能力［3］。利用傅里叶变换将图像从空间域转换到频域，提取图像形状在频域中的表示是一种有效的方法。但这类方法的检索性能紧密依赖于目标边界的提取结果，如果边界提取不准确，将会导致最终的检索准确率低，而且这种方法易受噪声等外部干扰的影响。

一般数字图像是通过正方形网格采样得到的，图像的坐标默认是笛卡尔直角坐标，且坐标原点在图像的左上角。直接对其进行傅里叶变换，虽然也能得到频谱描述，但是无法得到不变的形状描述子，即若对图像进行平移、缩放和旋转变换，将会得到不同的特征描述。

1 坐标系转换

给定一个二值图像I={f(x，y);0≤x＜M，0≤y＜N}，I的质心坐标(xc，yc)定义为

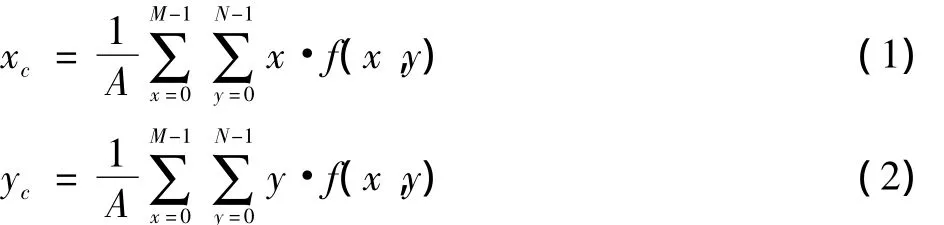
式中:A是图像面积，定义为

极坐标表示法以质心(xc，yc)为中心，由像素离质心的距离r和θ=0°所夹角度来表示像素的坐标(r，θ)。由笛卡尔直角坐标系转换为极坐标系的公式为

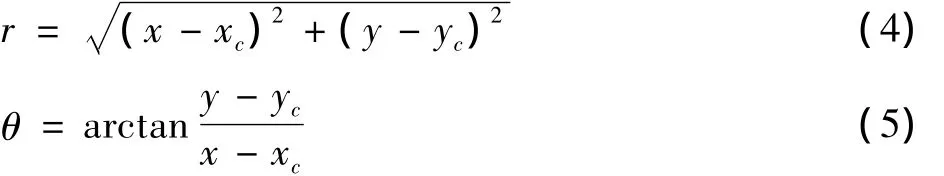
相比于直角坐标，极坐标表示图像的优点是不受图形平移和缩放的影响。

2 形状矩阵

形状矩阵是表示区域形状信息的一个有效工具。具体操作为:以质心为圆心，以最大质心距离为半径形成目标区域的最小外接圆。将圆半径等距离划分成M份，形成M个同心圆。之后将极轴从0°～360°逆时针旋转，记录极角为(K×360/N)°(K为0～N－1之间的整数)时极轴与同心圆交点处的像素信息。即使用极坐标光栅系统对图像进行重新采样，形成一个记录图像形状信息的、大小为M×N的形状矩阵。矩阵的行对应同心圆，列对应半径［4］。利用形状矩阵表示图像，大大减少了参与后续计算的数据量。由于极坐标的极点位于区域质心，且是对最大质心距离进行等距离划分，所以形状矩阵满足对图像的平移和缩放不变性［5］。

文献［5］提到，当图像发生旋转时，其对应形状矩阵的行向量将发生相应的循环移位。但分析形状矩阵的具体产生过程可以发现，若图像旋转某个角度，对其进行极坐标光栅系统采样后得到的形状矩阵也会发生变化，且这种变化并不是循环移位。图1通过仿真验证了本文的分析，其中图1c是对图1a顺时针旋转90°后得到的图形，图1b、图1d分别是图1a和图1c的形状矩阵。由图1可以清楚地看到，这两个矩阵的行向量之间并不存在循环移位关系。因此，文献［5］对形状矩阵进行相位修正，并不能保证描述子的旋转不变性，同时在进行相位修正后还会引入误差，这将直接导致检索的准确率降低。

图1 图形及旋转后图形的形状矩阵

3 二维离散傅里叶变换

图像I={f(x，y);0≤x＜M，0≤y＜N}的二维DFT定义为

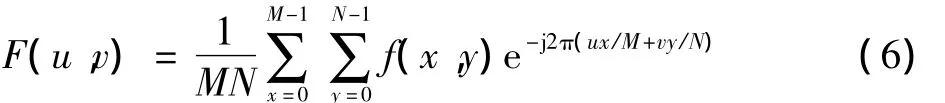
其幅度和相位分别为

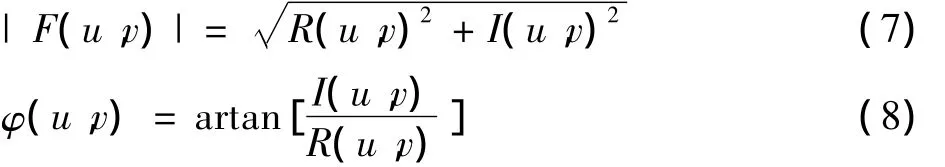
式中:R(u，v)是复数F(u，v)的实部;I(u，v)是虚部。

由DFT变换的性质可知，图像I平移后，幅度不发生变化，仅相位发生变化。因此一般情况下，可直接使用幅度信息描述形状。

4 实验结果和讨论

用于评估形状描述子性能的植物叶片图像主要从野外采集而来。典型的叶片形状如图2所示，其中包括三叶草、牵牛花、枫叶等8种植物叶子。每类图像采集30幅图片，其中20幅是同类不同个体的图像，另外10幅由从20幅图像中随机挑选的某几幅进行旋转、缩放、平移等几何变换得到。再加上一些不同形状的干扰叶片图像(如图2第2行所示)，组成一个300幅图像的小型形状数据库。其中，有些形状类似，如图1中第1行的形状5与第2行形状7相似，第1行形状3与第2行形状4相似，第1行形状6与第2行形状3相似，等等。

图2 典型的植物叶片形状

提取傅里叶描述子的具体步骤如下:

1)对彩色图像进行二值化。首先将图像库中的彩色图像转换为灰度图像，动态设定阈值，再将像素的取值二值化，获取二值图像f(x，y)。

2)求取图像的质心(xc，yc)。

3)坐标系转换。以质心为极坐标的极点，将图像的坐标系由直角坐标转变为极坐标系。

4)提取图像的形状矩阵。以质心为圆心，以最大极径为半径形成一个最小外接圆。将圆半径等距离划分成M份，极角分成N等分，形成大小为M×N的形状矩阵。

5)二维离散傅里叶变换。对形状矩阵进行二维离散傅里叶变换，得到形状矩阵在频域中的表示F(u，v)。

6)获取傅里叶描述子。获得幅度谱|F(u，v)|，将低频系数作为形状描述子。

在具体操作时，形状矩阵的大小M×N，以及低频系数的个数是根据检索性能进行确定的。实验取M=N=30，即形状矩阵的行数和列数都是30。由于图像的高频反映图像的细节内容，而低频部分反映图像的概貌，因此可以用傅里叶变换的低频系数作为表示图像形状的描述子。由于系数个数的多少也会对检索性能产生影响，因此实验分别取4，9，16，25，36，49 和64 个系数作为形状特征，并分别在测试集上进行检索。对6种不同形状各随机抽取4幅图像作为查询图像，分别在测试集上检索相似图像计算其查准率，求取平均值，得出每种形状的平均查准率，最后求取6种形状检索准确率的平均值。结果如图3所示，当特征数从4上升到16时，查准率上升了16个百分点，效果明显。而当特征数从16增加到64，准确率只上升了6个百分点，检索准确率增长缓慢。在对检索准确率和特征维数进行权衡后，本文将特征维数即系数个数确定为49。

图3 不同特征数下的平均查准率

为了测试本文算法的性能，实验将几种不同算法与之进行比较，包括Hu不变矩［6］、最小外接矩形(目标与最小外接矩形的面积比作为形状特征)［7］、最小外接圆(同心圆等面积划分N等份，再对每一区域求取信息熵作为形状特征)［8］、对图像边界的极坐标信息进行傅里叶变换得到的傅里叶描述子，以及PFD［5］这5种算法。

利用上述6种形状特征，分别对图2中的前6种形状进行检索，每类随机选取4幅图像作为查询图像，在剩余的图像中检索相似图像，计算平均查准率，绘制不同形状特征对不同叶子形状的平均检索查准率图(如图4所示)。图中行标识1～6分别代表6种不同形状，列代表查询准确率。从图4可以看出，除了形状5之外，本文算法对其余形状的检索准确率相较其他算法更加优越，尤其是形状1，3和4，但第6种形状的优势不明显。实验表明算法对于复杂形状的检索具有明显优势，原因在于形状矩阵中包含了图像形状较多的细节信息。6种形状特征的平均检索准确率分别为:71.25%，48.33%，55.00%，64.38%，77.5%，91.04%。由结果可以看出本文算法比查准率次高算法PFD的平均准确率高出13%以上。

最后为了测试噪声对算法性能的影响程度，实验分别对测试集中的图像添加高斯噪声和椒盐噪声，再统计6种叶片形状的平均检索准确率。具体数据如图5所示。从图中可以看出，具有噪声的图像的检索准确度大约下降10个百分点。分析原因在于噪声导致图像质心，尤其是最大极径发生改变，从而导致对应的形状矩阵发生改变，最终傅里叶描述子也发生相应变化。但是检索结果还是比较令人满意，原因在于算法利用傅里叶变换的低频系数作为描述子，而噪声对低频系数影响较小，因此，本文的算法对噪声具有一定的稳健性。

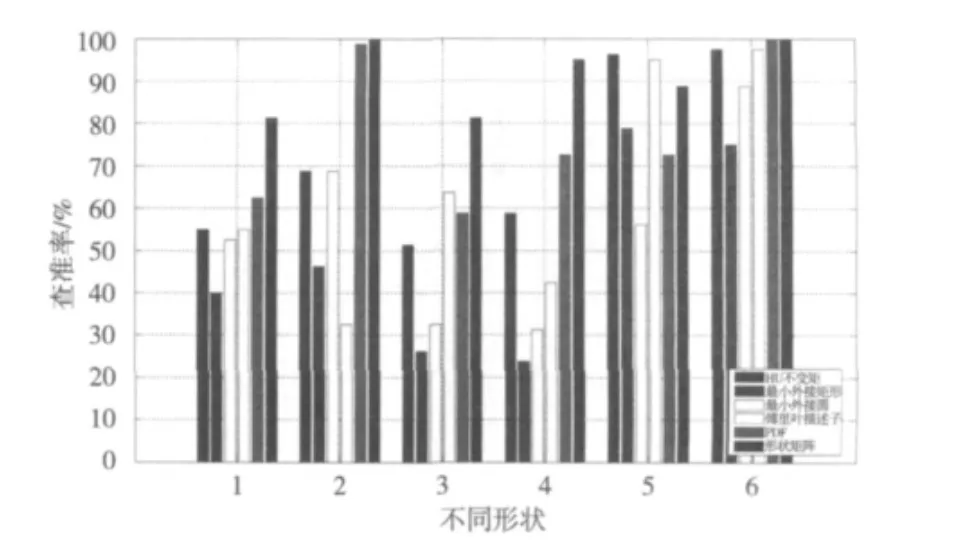
图4 不同形状特征对不同形状的平均检索查准率(%)

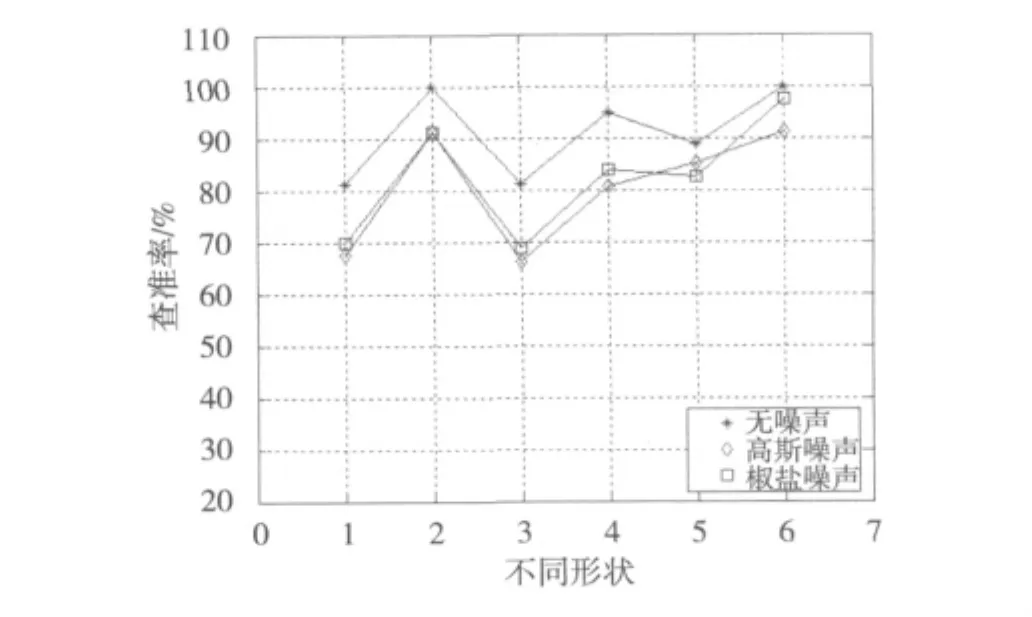
图5 噪声对检索性能的影响

5 结论

本文提出一种利用形状矩阵表示图像的空间域信息，之后进行二维离散傅里叶变换将形状信息从空域变换到频域，最后提取低频系数作为形状描述子的方法。用野外采集的植物叶子图像库进行测试实验结果显示，该算法要明显优于Hu不变矩等其他5种算法。但是如何增强本文算法对噪声的稳健性，以及使其对图像旋转具有不变性还有待进一步研究。

［1］闫雅楠，夏定元.结合边缘检测和区域分割的形状特征提取［J］.电视技术，2007，31(3):12－15.

［2］魏怡，何一伟，倪海峰，等.形状描述法在图像检索中的应用综述［J］.系统工程与电子技术，2009，31(7):1755－1761.

［3］ LU G J，SAJJANHAR A.Region－based shape representation and simlilarity measure suitable for content－based image retrieval［J］.Multimedia Systems，1999，7(2):165－174.

［4］GOSHTASB A.Description and discrimination of planar shape using shape matrices［J］.IEEE Trans.Pattern Anal.Mach.Intell.，1985，7(6):738－743.

［5］王斌.一种不变的基于傅立叶变换的区域形状描述子［J］.电子学报，2012，40(1):84－88.

［6］ HU M K.Visual pattern recognition by moment invariants［J］.IRE Trans.Information Theory，1962，11(2):179－187.

［7］卢蓉，范勇，陈念年.一种提取目标图像最小外接矩形的快速算法［J］.计算机工程，2010，36(23):178－180.

［8］孙强强.基于内容的二值商标图像检索研究［D］.扬州:扬州大学，2008.