车辆间通信信道的仿真模型分析

李世成，雷维嘉，陈 佳

(重庆邮电大学个人通信研究所，重庆 400065)

责任编辑:薛 京

随着无线通信技术的发展，人们对无线通信应用的范围和需求也随之扩展。作为智能交通系统研究中关键性的热点，车辆间通信越来越受到关注。车终端之间的通信带来了许多新的应用，如在加强道路交通安全上和减少交通对环境影响的应用［1］和商业服务以及车载娱乐中的应用［2－4］等。传统的车辆间通信系统需要架设交通信息中心来实现用户的接入，这不仅需要较大的基站辐射功率，而且网络中可能会存在传输的盲点，组网不够灵活。近年来人们试图将协作中继技术用于车辆间通信系统，以期望实现车辆间通信在没有交通信息中心的情况下灵活可靠地运作［5］。要研究快速变化信道中的车辆间通信，需要一个良好的在真实环境里测试过的物理层信道模型。

车辆间通信系统中的车终端与路边设施之间的信道属于平坦衰落信道，信道模型可采用传统平坦衰落信道模型，如瑞利信道、Nakagami信道、莱斯信道等。而由于车终端间环境和通信方式的特殊性，如信道的快速时变性、收发终端同时移动性和车终端天线较低等，车辆间的信道统计特性与传统的蜂窝无线网络有非常大的区别［6－8］。因此，找到合适的车辆间自组织网络信道模型仍然是一个研究的热点。文献［1］致力于网络层仿真与物理层仿真的结合研究，介绍了3种车辆间通信信道。文献［6］基于测试结果，提出了对5 GHz带宽的车辆间信道的技术规范。文献［7］描述了比较常用的信道模型方法，并侧重描述了统计性模型和基于地理信息的信道模型。

本文对在仿真中常用的3种车辆间信道的模型进行介绍，对其统计模型、适用场景等进行分析，并给出误码率的性能仿真结果。

1 无线信道的特征

在无线通信系统中，信源发射的电磁波经过不同的路径到达目的接收端，会产生“多径效应”。多径效应是发送电磁波与环境中的物体相互影响所造成的结果。在多径传播的条件下，由于不同路径的信号到达接收天线的时间不一样，因此接收的信号是由多个时延信号构成，会产生时延扩展。时延扩展是衡量多径传播信道质量的一个重要指标，具体定义为最大传输时延与最小传输时延的差值。在多径信道中，均方根(RMS)时延扩展τRMS是量化时延扩展最常用的参数，其定义为

时延扩展是由多径传播引起的现象，而相干带宽Bc是由均方根时延扩展得出的一个确定关系值。相干带宽是在一定范围内的频率的统计测量值，该频率范围内的任意两个频率分量受到的信道影响具有很强的相关性。若相干带宽内的各频率分量的相关函数值大于0.5，则相干带宽Bc与RMS时延扩展τRMS有如下关系［9］

如果发送信号带宽小于无线信道的相干带宽，那么接收信号经历的衰落过程就属于平坦衰落过程。在平坦衰落下，信道的多径特性会使发送信号的频谱结构在接收端保持不变，而多径信道增益的起伏，会使接收信号的强度随着时间变化。如果发送信号带宽大于信道的相干带宽，那么该信道特性会使得接收信号产生频率选择性衰落，并带来符号间干扰。

以上考虑的都是没有移动性的无线信道特性。当移动台与基站之间存在相对运动或信道路径中的物体处于运动中时，多径信道就会表现出时变特性。这种时变特性由多普勒扩展［10］和相干时间进行描述。

多普勒扩展BD是由移动通信信道的时变速率引起的频谱展宽程度的度量值［11－13］。如当发送信号频率为fc时，若收发端间存在相对运动，则接收信号频率会发生偏移，即多普勒频移。多普勒频移是移动台的相对速度v、移动台运动方向与散射波到达方向之间夹角θ的函数，即fd=vcosθ/λ，其中λ为载波波长。接收信号频谱展宽的大小依赖于多普勒频移fd。

相干时间Tc是在时域对多普勒扩展的表示，其与最大多普勒频移成反比，即

式中，fDmax是最大多普勒频移。相干时间是信道脉冲响应维持不变的时间间隔的统计平均值。在此时间间隔内，两个到达信号所受到的信道的影响具有很强的相关性。如果信号符号周期大于信道相干时间，那么在信号的传输中，信道特性会发生改变，产生时间选择性衰落。

2 车辆间信道分析

车辆间通信主要有两种方式:一种是车终端与路边设施的通信;另一种是车终端之间的通信。如图1所示，其中S为路边设施，M1，M2为两个不同的车终端。车终端与路边设施的通信信道可采用传统的衰落信道模型，如Nakagami信道、瑞利信道或莱斯信道模型来描述，本文不再进行介绍。本文主要对车终端之间通信的信道模型进行介绍。

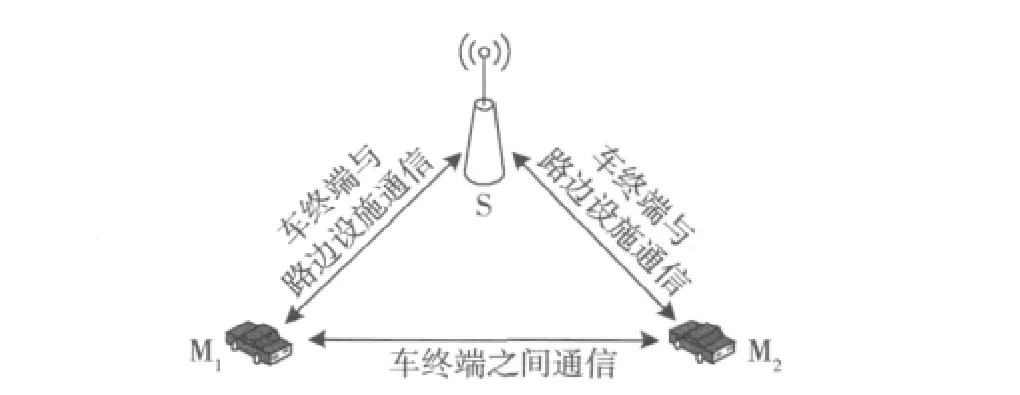
图1 车辆间通信的两种方式

车辆间通信的环境主要有城市环境和郊区高速环境两种，车辆间通信系统可分为窄带通信系统和宽带通信系统。在城市环境中的交通拥挤路段，由于车辆行驶速度较慢，可假设车终端间通信系统为准静态的窄带系统;而在城市环境交通非拥挤路段或在郊区高速环境中，车辆以较高速度行驶，车辆间信道时变较快，多普勒频移现象较明显，车终端间通信系统为宽带系统，车辆间信道可看成是双选择(即同时具有时间选择性和频率选择性)衰落信道。

2.1 车辆间通信的窄带系统

在城市环境中的交通拥挤路段，车辆行驶较为缓慢，而又比传统的移动终端快，当移动终端的覆盖范围在几十个载波波长之内时，信道状态可认为是准静态的［14］。一般性的车辆间通信散射模型［15］如图2所示。源终端S和目的终端D都处于移动状态，并且装配的天线高度水平位置较低。周围环境中不同物体会使源终端发送的信号发生散射，目的端接收到不同时延和衰落的信号。图2中，相互通信的两个车终端的周围各有一组各向同性分布的散射体，ss1，ss2，…，ssN表示源终端周围的散射体集，ds1，ds2，…，dsM表示目的终端周围的散射体集，dsd为源终端S和目的终端D之间的距离，Rs和Rd分别为源终端和目的终端的平均散射半径。假设Rs和Rd相对于dsd都很小，当两车终端之间的距离足够大，即Rs+Rd≪dsd时，可认为两组散射体之间相互独立。这样就在发送端和接收端分别产生N个和M个衰落过程，即发送终端到其周围散射体ss1，ss2，…，ssN的衰落过程和接收终端周围的散射体ds1，ds2，…，dsM到接收终端的衰落过程，当这两组衰落过程都分别合成为Nakagami衰落过程，那么发送端和接收端之间的信道为级联Nakagami信道［16－17］;当发送端和接收端的衰落过程分别合成为瑞利衰落过程，那么它们之间的信道为级联瑞利衰落信道［18］。

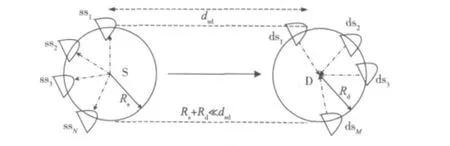
图2 各向同性的二维双环模型

2.1.1 级联Nakagami衰落信道

在城市环境中的交通拥挤路段，车终端周围均匀分布着散射体，若在源车终端周围和目的车终端周围分别产生两组Nakagami衰落过程，那么发送端和接收端之间的信道为级联Nakagami信道。

如图3所示，级联Nakagami信道衰落因子hSD服从级联Nakagami分布。该衰落因子为两个统计独立服从Nakagami分布的随机变量的乘积，即对于源端S到目的端D链路有hSD=hSD1hSD2，其中hSD1和hSD2服从参数不同的Nakagami分布。

图3 车辆间通信

hSD的概率密度函数为

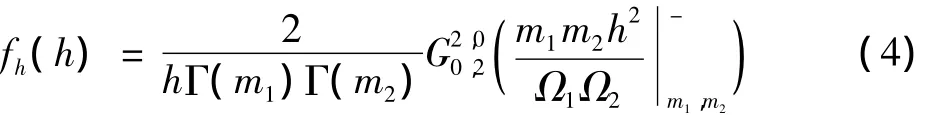
式中:ml是与信道衰落程度有关的参数，且l=1，2，当ml=1时，式(4)就简化为级联瑞利分布，方便起见省略了下脚标 SD;Γ(·)是伽马函数;G2，00，2是 Meijer G 函数，Meijer G函数是一种特殊函数，其一般性定义为

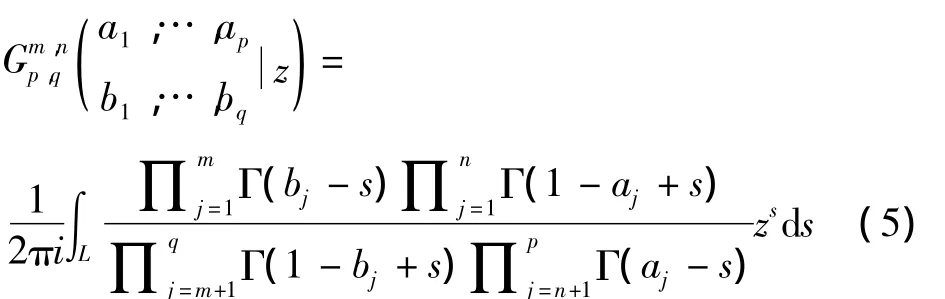
式中:0≤m≤q，0≤n≤p且m，n，p和q都是整数;对于k=1，2，…，n 和 j=1，2，…，m，有 ak－ bj≠1，2，3，…，n;z≠ 0［19］。

2.1.2 级联瑞利衰落信道

在城市环境中的交通拥挤路段，车终端周围均匀分布着散射体，若在源车终端和目的车终端分别形成两组瑞利衰落过程，那么发送端和接收端之间的信道为级联瑞利信道［17－22］。

在非视距通信的前提下，假设发送端和接收端周围的散射体数目足够大，即N和M的值都远大于1，级联瑞利信道的转移函数可表达为两个复高斯独立随机过程的乘积［23－24］，即

式中:α和γ是均值为0的复高斯随机变量。该转移函数的模值的概率密度函数为

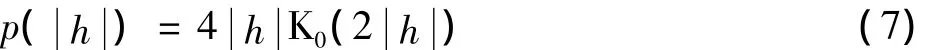
式中:K0()是修正后的第二类零阶贝塞尔函数［25］。修正后的第二类零阶贝塞尔函数积分表达式为

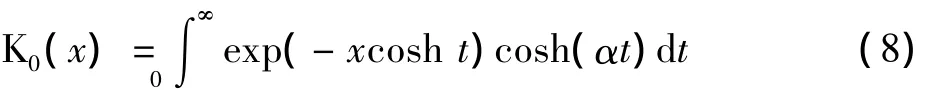
式中:cosh为双曲余弦函数。

2.2 车辆间通信的宽带系统

在城市环境中的非拥挤路段或在郊区高速环境中，两车终端周围各向同性地均匀分布着散射体，车上的天线高度是处于较低水平位置的。一方面，在该环境下车终端的高速移动性，使得传输信道特性快速变化，在一个符号周期内信道的快速变化，会产生信道的时间选择性衰落。发射机和接收机之间的相对运动会导致信道快速时变，且移动速度越快，信道的时变特性越显著。另一方面，由于数据率越高，符号周期越短，信号带宽越宽，当信号带宽大于信道的相干带宽时，将产生频率选择性衰落。当车辆高速移动时，目前的通信系统往往只能提供低速率传输服务，难以实现高速率的数据传输［26］。如果此时信道满足2fdτd＜1，那么该信道可被认定为双选择衰落，其中fd为多普勒扩展，τd为时延扩展［27－30］。在此情况下，时频双选择性衰落对车辆间通信的影响较大。

文献［26－27，31］提出基扩展模型(BEM)适合作为双选择衰落信道的仿真模型，该模型由式(9)给出。对于接收到的信息序列，将其以Ts为采样周期进行采样，PTs为数据块间隔，即每个数据块包括P个采样符号。利用实际信道的多普勒频率扩展的有限带宽性质，把一个数据块内的时变多径信道变化，用数量很少的块内时不变的参数来描述。基扩展模型表达式为

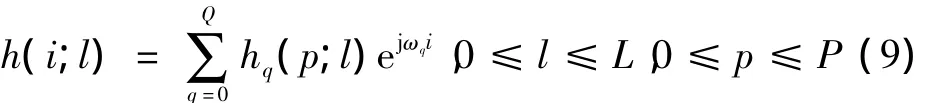
式中:h(i;l)表示第i个符号每一径上的信道增益;ωq=2π(q － Q/2)/P;L=，τmax是最大时延扩展;Q=，fmax为最大多普勒频移。式(9)用Q+1个Fourier基来捕获每一径上的时变特性，也就是说每一径的时变信道，用Q+1个基的系数表示，通常Q的取值很小(2或4)，那么用较少数量的(Q+1)(L+1)个系数hq，l就可以描述整个块内时变多径信道。

3 各信道性能的仿真

3.1 Nakagami信道、瑞利信道与级联Nakagami信道、级联瑞利信道性能

仿真时，发送信号均采用BPSK调制，假设接收端已知信道状态信息，信道噪声为高斯白噪声。Nakagami信道仿真时，参数m分别取值0.5和2，方差为1［32］;级联Nakagami信道衰落因子由两个服从Nakagami分布的变量相乘得来，这两个变量的均值m同取0.5和2。瑞利信道即m=1时的Nakagami信道，级联瑞利信道即两个m值同时取1时的级联Nakagami信道。仿真结果如图4所示。

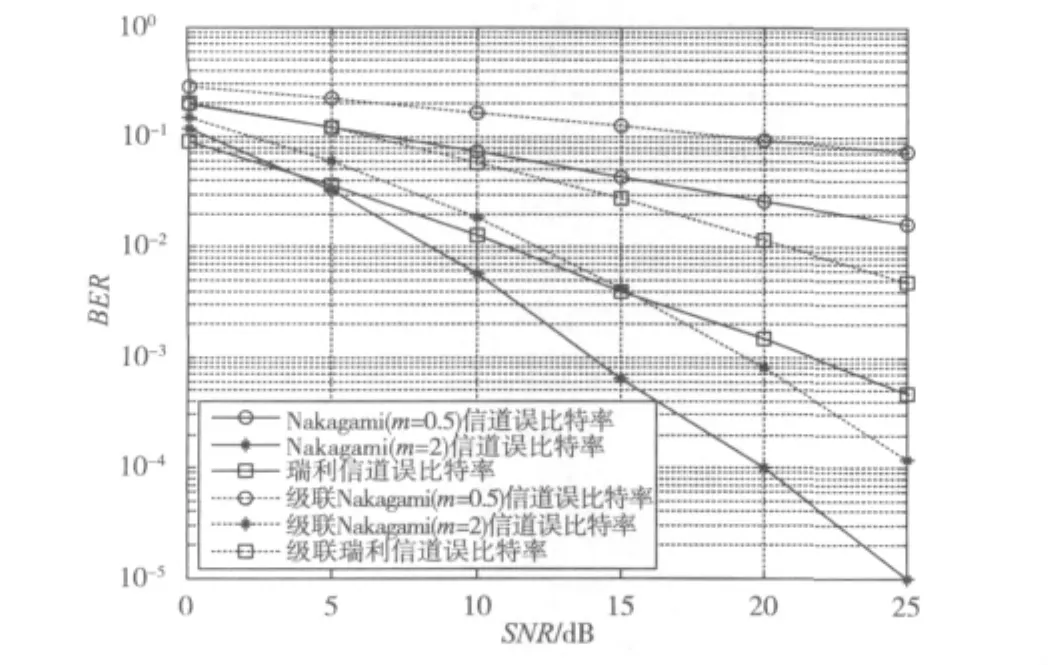
图4 Nakagami信道、瑞利信道与级联Nakagami信道、级联瑞利信道误码率性能的比较

由图4中曲线对比可知，随着参数m的增大，级联Nakagami信道误码率逐渐降低。级联Nakagami(m=2)信道的误码率比级联瑞利信道低，而级联Nakagami(m=0.5)信道误码率比级联瑞利信道的高，并且随着m值和信噪比值的增加，误码率之间的差别都在逐渐增大。由此说明，随着参数m值的增加，级联Nakagami信道的衰落程度在减小。在m值取相同值时，级联Nakagami信道的误码率性能比Nakagami信道的要差，说明此时级联Nakagami信道比Nakagami信道的衰落程度更深，车辆间通信信道比传统的移动通信信道有更严重的衰落。

3.2 双选择信道性能分析

针对双选择信道的情况，文献［26］提出了一种用于信道估计的优化训练序列的设计方案，随后仿真了该信道的误码率性能，并与理想信道特性估计时的误码率进行了比较，如图5所示。仿真中采用的系统:信道估计的数据块长度为300个符号，每个传输数据块进行1次信道估计，载波频率fc=2 GHz，符号采样周期为10 μs，最大移动速率为160 km/h，根据Q=2，计算得到Q=2。假设信道经过7条径(L=6)的瑞利衰落信道，信道各径延迟功率相同，信道总能量归一化，系统采用QPSK调制，采用MMSE均衡算法进行均衡。

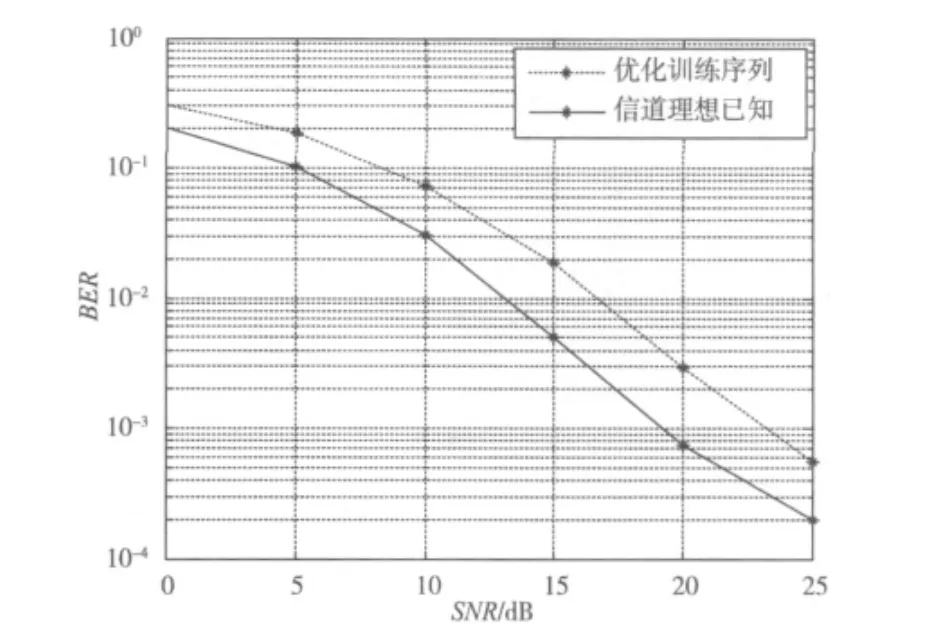
图5 双选择信道误码率

由图4和图5对比可知，信道理想且已知时的双选择信道的误码率性能优于级联瑞利信道。这是由于对于双选择衰落信道模型，在信道信息为理想已知的前提下，发送的信号经过7条瑞利信道到达接收端，在接收端进行均衡出来后，可形成分集效果，使得接收到的信号得到加强，因此信道理想且已知时的双选择信道性能要优于级联瑞利信道。另外，从图5可知，利用优化训练序列估计得出的信道信息进行均衡，与利用理想信道信息进行均衡的系统间在误码性能上有3 dB以上的差距，表明信道估计的性能对双选择信道系统性能有较大的影响。而在实际应用中，由于信道衰落的快速变化，信道估计困难，会存在较大的估计误差，因而双选择信道环境下的车辆间通信系统的误码性能实际上要远比图5中理想已知信道信息时的性能差。

4 小结

本文介绍了无线信道的特征和移动无线信道的特点以及它们主要的物理层影响，重点描述了3种常用的车辆间通信信道的特征，并对其进行了误码率的性能仿真。仿真结果表明，相比较一般的无线信道，车辆间通信信道的衰落更为严重。另一方面，车辆间通信环境不同时，信道的性能也存在很大的差别。因此，对于车辆间通信进行研究时，应根据不同的环境选用适合的信道模型。

［1］ BOEGLEN H，HILT B，LORENZ P.A survey of V2V channel modeling for VANET simulations［C］//Proc.8th International Conference on Wireless On－Demand Network Systems and Services，2011. ［S.l.］:IEEE Press，2011:117－123.

［2］ YOUSEFI S，CHAHED T，LANGARI S M M，et al.Comfort applications in vehicular Ad Hoc networks based on fountain coding［C］//Proc.IEEE 71st Vehicular Technology Conference，2010.［S.l.］:IEEE Press，2010:1－5.

［3］ CATALDI P，TOMATIS A，GRILLI G，et al.A novel data dissemination method for vehicular networks with rateless codes［C］//Proc.IEEE Wireless Communications and Networking Conference，2009. ［S.l.］:IEEE Press，2009:1－6.

［4］ SARDARI M，HENDESSI F，FEKRI F.DMRC:dissemination of multimedia in vehicular networks using rateless codes［C］//Proc.IEEE INFOCOM Workshops 2009.［S.l.］:IEEE Press，2009:1－6.

［5］李兆训.频率选择性衰落信道下基于协作分集的车际通信［J］.信息工程大学学报，2007，8(4):439－442.

［6］ MATOLAK D W.Channel modeling for vehicle－to－vehicle communications［J］.IEEE Communications Magazine，2008，8(5):76－83.

［7］ MOLISCH A，TUFVESSON F，KAREDAL J，et al.A survey on vehicleto－vehicle propagation channels［J］.IEEE Wireless Communications，2009，16(6):12－22.

［8］ PATEL C S，STUBER G L，PRATT T G.Simulation of rayleigh－faded mobile－to－mobile communication channels［J］.IEEE Trans.Communicaitons，2005，53(10):1876－1884.

［9］RAPPAPORT T S.无线通信原理与应用［M］.周文安，付秀花，王志辉，等，译.北京:电子工业出版社，2006.

［10］ ACOSTA G，INGRAM M A，TOKUDA K.Measured joint Doppler－delay power profiles for vehicle－to－vehicle communications at 2.4 GHz［C］//Proc.IEEE Global Telecommunications Conference，2004. ［S.l.］:IEEE Press，2004:3813－3817.

［11］ PROAKIS J G，SALEHI M.Digital communications［M］.4th ed.［S.l.］:McGraw－Hill，2001.

［12］ JAKES W C.Microwave mobile communications［M］.［S.l.］:Wiley－IEEE Press，1994.

［13］ STUBER G L.Principles of mobile communication［M］.New York:Springer Science/Business Media，2001.

［14］ PATZOLD M.Mobile fading channels［M］.Umich:J.Wiley，2002.

［15］ AKKI A，HABER F.A statistical model of mobile－to－mobile land communication channel［J］.IEEE Trans.Vehicular Technology，1986，35(1):2－7.

［16］ ILHAN H，UYSAL M，ALTUNBAS I.Cooperative diversity for inter vehicular communication:performance analysis and optimization［J］.IEEE Trans.Vehicular Technology，2009，58(7):3301－3310.

［17］ KARAGIANNIDIS G K，SAGIAS N C，MATHIOPOULOS P T.N*Nakagami:A novel stochastic model for cascaded fading channels［J］.IEEE Trans.Communications，2007，55(8):1453－1458.

［18］ DEY I，NAGRAJ R，MESSIER G G，et al.Performance analysis of relayassisted mobile－to－mobile communication in double or cascaded Rayleigh fading［C］//Proc.IEEE Pacific Rim Conference on Communications，Computers and Signal Processing，2011. ［S.l.］:IEEE Press，2011:631－636.

［19］ Meijer G－function［EB/OL］.［2012－04－10］.http://en.wikipedia.org/wiki/Meijer_G－function.

［20］ LI Zhaoxun，JIA Longzhen，LI Feng，et al.Outage performance analysis in relay－assisted inter－vehicular communications over double－Rayleigh fading channels［C］//Proc.International Conference on Communications and Mobile Computing，2010.［S.l.］:IEEE Press，2010:266－270.

［21］ KOVACS I Z.Radio channel characterisation for private mobile radio systems:mobile－to－mobile radio link investigations［D］.Aalborg，Denmark:Aalborg University，2002.

［22］ KARAGIANNIDIS G K，TSIFTSIS T A，SAGIAS N C.A closed form upper－bound for the distribution of the weighted sum of Rayleigh variates［J］.IEEE Communications Letters，2005，9(7):589－591.

［23］ UYSAL M.Maximum achievable diversity order for cascaded Rayleigh fading channels［J］.IEEE Electronics Letters，2005，41(23):1289－1290.

［24］ SEYFI M，MUHAIDAT S，LIANG J.Relay selection in dual－hop vehicular networks［J］.IEEE Signal Processing Letters，2011，18(2):134－137.

［25］ GRADSHTEYN I S，RYZHIK I M.Table of integrals，series and products［M］.San Diego:Academic Press，2007.

［26］刘英男，蒋伟，姚春光，等.基于理想自相关训练序列的双选择信道估计［J］. 电子与信息学报，2008，30(10):2423－2426.

［27］ MA X L，GIANNAKIS G.Maximum－diversity transmissions over doubly selective wireless channels［J］.IEEE Trans.Information Theory，2003，49(7):1832－1840.

［28］KOZEK W.On the transfer function calculus for underspread LTV channels［J］.IEEE Trans.Signal Process，1997，45(1):219－223.

［29］ FETEIHA M F，UYSAL M.Multipath－Doppler diversity for broadband cooperative vehicular communications［C］//Proc.IEEE International Conference on Communicaitons，2011.［S.l.］:IEEE Press，2011:1－6.

［30］ FETEIHA M F，UYSAL M，AHMAD A R.Cooperative inter－vehicular communications in highway traffic［C］//Proc.24th Canadian Conference on Electrical and Computer Engineering，2011. ［S.l.］:IEEE Press，2011:460－465.

［31］ BARHUMI I，LEUS G，MOONE M.Time－varying FIR equalization of doubly selective channels［C］//Proc.IEEE International Conference on Communications，2003.［S.l.］:IEEE Press，2003:3246－3250.

［32］ Nakagami distribution［EB/OL］. ［2012－04－10］.http://en.wikipedia.org/wiki/Nakagami_distribution.