两类最优跳频序列集的线性复杂度

高军涛，胡予濮，李雪莲，向上荣

(1. 西安电子科技大学 计算机网络与信息安全教育部重点实验室，陕西 西安 710071；2. 中国科学院 软件研究所 信息安全国家重点实验室，北京 100190；3. 西安电子科技大学 应用数学系，陕西 西安 710071；4. 西安电子科技大学 计算机学院，陕西 西安 710071)

1 引言

跳频(FH)序列在扩频通信和码分多址(CDMA)通信系统中都有广泛的应用。跳频码分多址系统(FH-CDMA)被广泛地应用于蓝牙、雷达系统等方面。在这些系统中，信号接收者面临的主要问题就是信号之间的相互干扰。针对这种情况，人们一般采用具有低Hamming相关的跳频序列集来降低干扰，提高系统的性能。除此之外，在实际应用中，特别是在军用系统中，人们不希望自己传送的信息被怀有敌意的人获得或者蓄意干扰。为了抵抗干扰和增加保密性，跳频序列除了应该具有低的Hamming相关以外，还应该具有较大的线性复杂度[1]。线性复杂度是衡量序列安全性的一个重要指标。如果一个序列的线性复杂度很低，即使它有大的周期，也很容易受到Berlekamp-Massey算法的攻击，因而序列的使用者就没有秘密可言。另一方面，为了降低通信收发双方的实现复杂度，跳频序列的实现应该尽量简单。因此设计实现简单，低Hamming相关且高线性复杂度的跳频序列集就具有重要的意义。

当前有许多种类的最优跳频序列集[2～11]，这些跳频序列集有的是用代数方法设计的[2～6]，有的则是用组合数学方法设计的[7～11]。所有这些集合中序列间的Hamming相关满足Lempel-Greenberger界[12]或 Peng-Fan界[13]。在这些序列集中有些序列的线性复杂度很小[2～4]，有些序列的线性复杂度仍然没有结论[7～11]，使得这些跳频序列不能应用于保密通信中[14]。虽然当前存在具有高线性复杂度的最优跳频序列集[5,6]，但这些序列集是通过广义 Bent函数或者多项式环构造的，实现相对比较困难。因此如何将低线性复杂度的最优跳频序列集变换为具有高线性复杂度的最优序列集，同时保证序列实现简单，就成为一个亟待解决的问题。

为了提高跳频序列的线性复杂度，Ding和Yin[2]指出人们可以使用有限域中的幂置换[15]将一个具有低线性复杂度的跳频序列集变换为一个具有较高线性复杂度的跳频序列集。在文献[16]中，Wang研究了三类最优跳频序列集在幂置换下的线性复杂度，指出这三类序列集中序列的线性复杂度在幂置换下可以大幅增加。Wang同时指出：“除了幂置换以外，其他类型的置换多项式也有可能增加序列的线性复杂度，但计算这些序列线性复杂度的精确值并不容易”。

本文利用有限域中另一类置换多项式δ(x)来提高序列的线性复杂度，通过理论证明给出了置换以后得到的序列线性复杂度的精确值。结果表明，这类置换多项式可以使变换后序列的 Hamming相关保持最优，而且还大幅度地增加了序列的线性复杂度。因此证明了Wang提出的命题，即其他类型的置换多项式也可以提高序列的线性复杂度，得到序列线性复杂度的精确值。本文得到的新型跳频序列集的工程实现是比较简单的，同时具有高的线性复杂度。与现有的具有大线性复杂度的跳频序列集[5,6,16]相比，本文的序列具有如下的优点：①相比于文献[5,6]中最优跳频序列集，我们这类序列集的实现更为简单。②与文献[16]中幂置换后的最优跳频序列集相比，本文给出的新型最优跳频序列集的实现复杂度与幂置换后序列的实现复杂度相当，而线性复杂度比大部分幂置换给出的序列的线性复杂度要更高，比少数幂置换给出的序列线性复杂度低。详细的对比情况参见本文第4节。

2 基础知识

2.1 最优跳频序列

设 l是一个正整数，一个有限集合 F定义为F={f0, f1,…, fl-1}。令长度为 n 的序列 X=x0x1… xn-1，其中xi∈F。长度为n的所有跳频序列组成的集合记为 S={X| X=x0x1…xn-1，其中 xi∈F}。∀X, Y∈S，它们之间的Hamming相关定义如下：

其中，如果xi=yi+t，则h[xi, yi+t]=1；否则h[xi, yi+t]=0。由式(1)集合S中的Hamming相关可以定义如下[1]：

一个跳频序列的Hamming相关如果满足式(5)，称其满足Lempel-Greenberger界。

引理1[12]对于F上的每一个长度为n的跳频序列X，其Hamming相关满足

其中，ε是n模l的最小非负剩余，即ε≡n mod l。

满足Lempel-Greenberger界的单个序列称为最优跳频序列。

为了判断一个跳频序列集是否达到最优，还需要用到引理2。

引理2[13]设S是包含N个长度为n的跳频序列组成的集合，跳频序列中分量取自集合F。定义，则

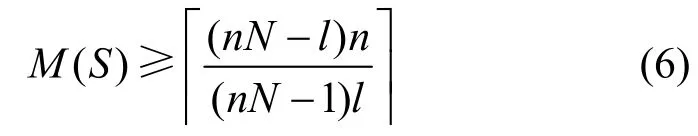
并且

一个跳频序列集的Hamming相关值如果满足式(6)或者式(7)，则称这类序列集满足Peng-Fan界。满足Peng-Fan界的跳频序列集称为最优跳频序列集。

2.2 序列的线性复杂度

设GF(q)表示含有元素个数为q的有限域，GF(q)*表示GF(q)中所有的非零元，这里q=pr，p是一个素数，r≥1是一个正整数。对于一个元素取自GF(q)上的序列s=s0s1…，其线性复杂度可以定义为产生该序列最短的线性反馈移位寄存器(LFSR)的长度。设序列s由一个LFSR生成，并满足递归关系式：sn+l=cl-1sn+l-1+cl-2sn+l-2+…+ c0sn，n≥0。多项式c(x)=clxl+ cl-1xl-1+…+ c1x+c0称为序列s的特征多项式。显然满足上述递归关系的特征多项式有很多，其中具有最低次数L的特征多项式称为序列s的最小多项式。序列s的线性复杂度还可以定义为其最小多项式的次数，记为LS(s)=L。

线性复杂度是衡量序列安全性的一个重要指标。如果一个序列具有较低的线性复杂度，那么序列可以由较短的LFSR来生成，攻击者利用Berlekamp-Massey算法可以很容易得到生成该序列最短的LFSR长度和它的反馈逻辑，因此，高线性复杂度是序列安全的一个必要条件。从工程角度来说，线性复杂度可以认为是利用LFSR生成序列的困难程度。

3 主要结果

对于一个最优跳频序列或者最优跳频序列集来说，线性复杂度是一个重要的指标。当前存在具有较高线性复杂度的跳频序列集[5,6]，但这些跳频序列是通过广义bent函数或者多项式环设计的，在实际应用中实现并不简单。在文献[16]中，Wang利用有限域GF(q)上的幂置换：x→xσ，这里x∈GF(q)，gcd(σ, q-1)=1，提高几类序列的线性复杂度。Wang同时指出“或许”可以利用其他类型的置换多项式来提高序列的线性复杂度，但计算线性复杂度并不像幂置换那么容易。本文利用下面的置换研究两类最优跳频序列的线性复杂度。

引理3[15]当q为奇数时，多项式x(q+1)/2+bx∈GF(q)[x]是GF(q)上的一个置换多项式当且仅当b=(c2+1)(c2-1)-1，这里c∈GF(q)，c≠0，c2≠1。

上述引理中的置换多项式和幂置换显然是不同的。因此给出的具有高线性复杂度的最优跳频序列集是一类新的跳频序列集。

3.1 第一类跳频序列集

设p是个奇素数，q=pr，r是一个正整数，m≥3是一个奇数。假设α是GF(qm)*的生成元，n= (qm-1)/2，d是一个整数满足gcd(d, qm-1)=1。令β=α2d，∀a∈GF(qm)，定义一个序列sa如下：

其中，Tr(x)=x+xq+…+xqm-1是GF(qm)→GF(q)上的迹函数。文献[3]已经证明：sa是一个((qm-1)/2,(qm-1-1)/2; q)最优跳频序列。{sa, sa’}是一个(( qm-1)/2,2, (qm-1-1)/2; q) 最优跳频序列集，这里a是GF(qm)*中某个元素的平方，而a’不能表示为GF(qm)*中某个元素的平方。文献[16]证明了这些序列的线性复杂度等于m。相比于序列的周期( qm-1)/2来说，该序列的线性复杂度非常低，下面证明可以利用置换多项式来得到具有大线性复杂度的跳频序列集。

引理4[17]

引理5[18]设f(x) ∈GF(q)[x]，f(x)在其分裂域上的全部根记为α1，α2，…，αn。序列a=a0a1…以f(x)为特征多项式当且仅当存在一组元素λ1，λ2，…，λn，使得

序列a的线性复杂度等于上式中不等于0的那些λi的个数。

该引理表明一个序列中的元素可以由序列特征多项式的根来表示，并且序列的线性复杂度也可以由序列根表示的数目确定。

引理6[19]设f(x) ∈GF(q)[x]，f(x)在其分裂域上无重根。则f(x)可以表示为f(x)= f1(x) f2(x)…fk(x)，k＞0，fi(x)，i=1,2,…k，是GF(q)上不同的不可约多项式。设序列s是以f(x)为极小多项式生成的序列，则序列s可以表示为s=s(1)+s(2)+…+s(k)，其中s(i)是以fi(x)为极小多项式生成的序列。

定理1 设序列sa由式(8)给出，b=(c2+1)(c2-1)-1，这里c∈GF(q)，c≠0，c2≠1。设δ(x)= x(q+1)/2+bx，定义

0≤t≤(qm-1)/2-1则

1) (δ(sa), δ(sa’))组成一个((qm-1)/2, 2, (qm-1-1)/2;q) 最优跳频序列集。

2) δ(sa)的线性复杂度为

证明

定理1中的1)是显然成立的。因为δ(x)：GF(q)→GF(q)是GF(q)上的置换多项式，所以序列δ(sa)是序列sa的置换序列。根据式(1)中Hamming相关的定义，δ(sa)满足引理1中的最优界。下面证明定理1中的2)部分。

因为q=pr，(q+1)/2可以表示为

所以

根据引理4，

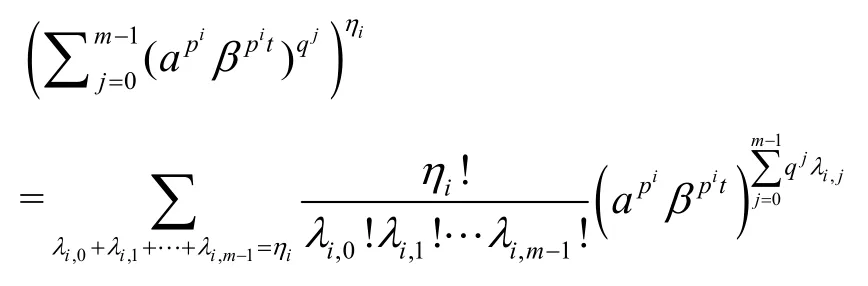
所以

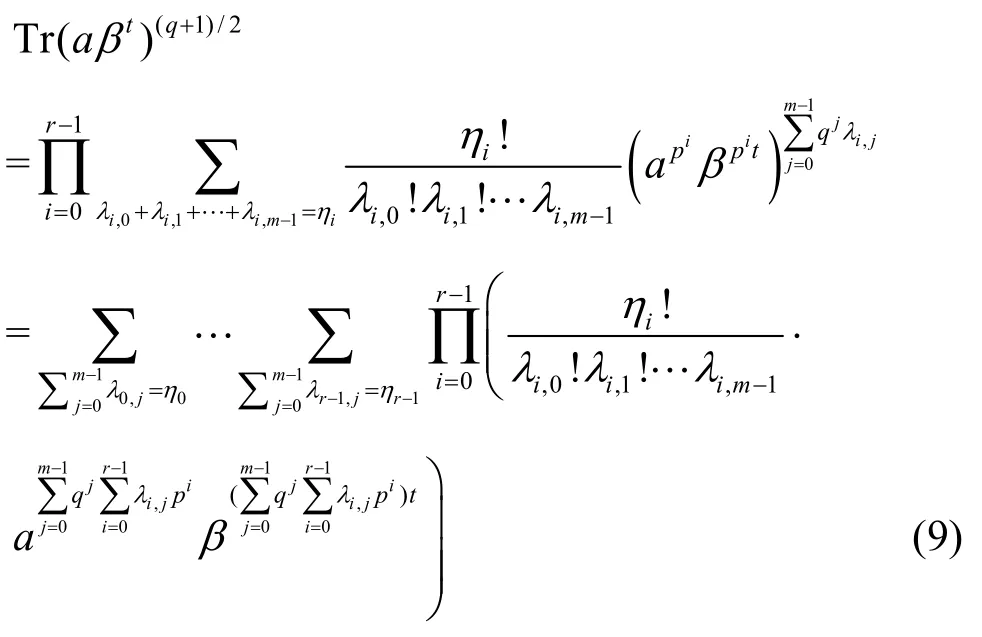
根据引理5，需要给出式(9)中β的系数模qm-1有多少是互不相同的。对于不同的λi,j，λ′i,j考虑式(10)：

因为λi,j≤ηi，λ'i,j≤ηi并且当q＞3时有：

由式(10)可知，

对于上式把等号两边模q得到：

显然，式(12)等号两边的值都是小于q的，所以mod q可以省去。得到λ0,0=λ′0,0, λ1,0=λ′1,0, …,λr-1,0=λ′r-1,0。同理，对式(11)两端同时模qk, k=2,3, …, m-1, 可以得到 ∀i, j, λi,j=λ′i,j，这与λi,j≠λ′i,j矛盾。因此证明了式(9)中β的次数是互不相同的。

下面证明序列bTr(aβt)中的β的次数与式(9)中β的次数是互不相同的。因为

所以，Tr(aβt)中β的次数形式为qkt。假设存在λi,j使下式成立：

显然上式左边和qk都是小于qm-1的，所以mod(qm-1)可以省略。因为所有的0≤λi,j≤ηi，要使得上式成立，必须有λ0k=1且其余的λi,j=0，这就意味着 η0=1，ηi=0， i=1, 2,…, r-1，即(q+1)/2=1。这与p是奇素数，q是p的幂次矛盾。因此Tr(aβt)(q+1)/2与bTr(aβt)中β的次数都互不相同。

为了计算δ(sa)的线性复杂度，根据引理5必须给出δ(sa)的表示中系数不为0的β的个数。因为

根据组合数公式[17]，共有：

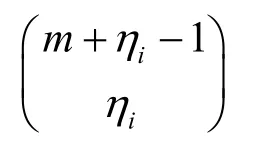
个方式将ηi表示为满足条件的λi,j的和。

因此，Tr(aβt)(q+1)/2中共含有以下数目的项：

又因为bTr(aβt)中β的幂次与Tr(aβt)(q+1)/2中的完全不同，由引理6序列δ(sa)的线性复杂度为

从式(13)可以看出，线性复杂度的提高依赖于(q+1)/2的分解。因为q=pr，所以

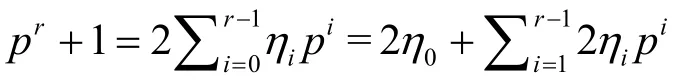
因此可以确定

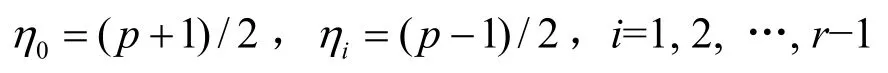
当p、r、m 3个参数固定时，δ(sa)的线性复杂度是固定的，即

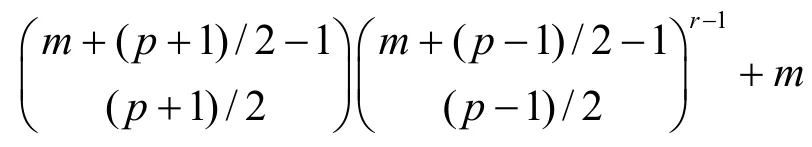
显然，相比于原来的线性复杂度，置换以后的序列线性复杂度有明显的提高。证毕。

3.2 第二类跳频序列集

设p是一个素数，q=pr，r是一个正整数。设m和d是2个正整数，满足d | qm-1，并且gcd((qm-1)/(q-1), d)=1。假设α是GF(qm)*的生成元，β=αμd，μ是一个正整数满足gcd(qm-1, μ)=1，设n= (qm-1)/d，对于每一个0≤i≤d-1，可以定义下面的序列：

文献[2]已经证明了由序列

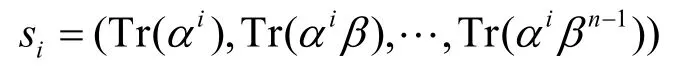
组成的序列族S={si|0≤i≤d-1}是一个((qm-1)/d, d,( qm-1-1)/d; q)最优跳频序列集。

由参数β，α，d，μ的定义可以看出，式(14)中的序列是式(8)中序列的一种广义描述。第二类跳频序列集中要求gcd(qm-1, μ)=1，d | qm-1；而第一类跳频序列集中gcd(qm-1, d)=1，2 | qm-1；第一类序列可以看作是第二类序列中d=2时的一个特例，因此第二类跳频序列集可以看作是第一类跳频序列集的推广。文献[16]证明这些序列的线性复杂度等于m。相比于序列的周期来说，该线性复杂度显然是非常低的。利用的置换多项式δ(x)和第一类序列集同样的方法，可以改进第二类序列集的线性复杂度，所以有定理2。

定理2 设序列si由式(14)给出，b=(c2+1)(c2-1)-1，这里c∈GF(q)，c≠0，c2≠1。设δ(x)=x(q+1)/2+bx，定义

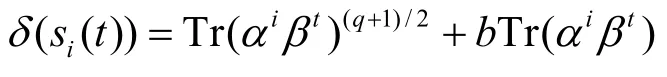
则

2) δ(sa)的线性复杂度为

定理2的证明与定理1类似，略去。

可以看出，利用置换多项式δ(x)可以将低线性复杂度的最优跳频序列集转化为高线性复杂度的最优跳频序列集。例如：当p=7，q=73，m=5，在原序列集中线性复杂度仅为5，而经过δ(x)=x(q+1)/2+bx置换以后得到的新跳频序列集的线性复杂度等于85 755，显然大幅度增加了序列的线性复杂度。

4 比较和实现

本节主要将本文给出的最优跳频序列集与现有的具有高线性复杂度的最优跳频序列集[5,6,16]从线性复杂度和工程实现2个角度进行对比，说明本文给出的跳频序列集具有的优势。

由式(8)和式(14)可以看出，置换前的两类跳频序列集都可以通过迹函数来实现。众所周知，当迹函数中只包含一个元素的幂次时，其工程实现是非常简单的。但由于这两类跳频序列集的线性复杂度太低，因此只能限制在保密要求很低的环境中使用。本文置换以后的跳频序列集，是在原序列集上增加了一个(q+1)/2乘幂次运算(即增加的乘法次数约为log ((q+1)/2)次)，而后与原序列输出相加。这种改变仅仅增加了一个简单的乘法电路和一次加法运算，其中加法运算由于运算量非常小是可以忽略不计的，可见置换以后跳频序列的工程实现仍然是非常简单的，以增加非常少量的实现复杂度来获得较高的线性复杂度是非常值得的。

文献[5]利用广义bent序列和广义bent函数构造了两类具有高线性复杂度的最优跳频序列集。其中第一类最优跳频序列集的线性复杂度并不是太高(当周期为p的幂次时，线性复杂度仅为p)，第二类最优跳频序列集的线性复杂度相比于第一类较高。然而因为这两类序列集都是基于广义 bent函数或者广义bent序列构造的，所以实现是比较复杂的[20]。

文献[6]的目的也是构造具有高线性复杂度的最优跳频序列集，这种构造主要是基于代数中的多项式环理论，相比于文献[2,3]中利用有限域构造的最优跳频序列集来说，这种基于环构造的最优跳频序列本身更加的复杂，并且实现也不简单，但这种构造可以获得较高的线性复杂度，在保密性要求较高的环境中可以使用该类跳频序列集。

文献[16]是利用幂置换将具有低线性复杂度的最优跳频序列集置换为具有高线性复杂度的最优跳频序列集，其工程实现也相对简单，仅仅是在原序列上增加一个σ (满足 gcd(σ, q-1)=1) 的幂次运算，增加的乘法次数约为log σ次。而本文给出的新型最优跳频序列的实现大约需要增加 log ((q+1)/2)次乘法和一次加法运算。因此本文序列的实现复杂度与文献[16]中序列的实现复杂度大致相当。在线性复杂度方面，由文献[16]中的结论，置换后序列线性复杂度的值取决于σ 的 p元表示，而且当σ=pr-pj-1时，序列的线性复杂度取到最大。本文利用置换多项式δ(x)得到置换后跳频序列线性复杂度的值依赖于(q+1)/2的p元表示，因此有限域给定时，置换后序列的线性复杂度就是给定的。由本文定理1、定理2和文献[16]中定理5、推论6、定理9、推论 10中的结论可以看出：本文给出的新型最优跳频序列的线性复杂度要小于幂置换σ =pr-pj-1时序列的线性复杂度，但要大于大多数使用其他幂置换得到的最优跳频序列的线性复杂度。

综上所述，利用δ(x)可以将两类低线性复杂度的最优跳频序列集变换为具有高线性复杂度的最优跳频序列集，与现有的具有高线性复杂度的最优跳频序列集相比，增加了非常少的实现复杂度，获得了较高的线性复杂度。

5 结束语

本文主要证明了Wang给出的命题[16]，即除幂置换以外，其他类型的置换多项式也可以给出具有大线性复杂度，实现相对简单的最优跳频序列集，并且可以给出置换后序列线性复杂度的精确值。由定理1和定理2的结论可以看出，利用置换多项式δ(x)= x(q+1)/2+bx可以将低线性复杂度的最优跳频序列集转化为具有高线性复杂度，实现简单的最优跳频序列集。通过计算序列表示中α不同幂次的数目，给出了这些序列线性复杂度的精确值。本文利用的置换δ(x)与文献[16]中使用的幂置换显然是不同的，因此得到的是新型的最优跳频序列集。

[1] SIMON M K, OMURA J K, SCHOLZ R A, et al. Spread Spectrum Communications Handbook[M]. New York: McGraw-Hill, 2002.

[2] DING C, YIN J. Sets of optimal frequency-hopping sequences[J].IEEE Transactions on Information Theory, 2008, 54(8): 3741-3745.

[3] DING C, MOISIO M J, YUAN J. Algebraic constructions of optimal frequency-hopping sequences[J]. IEEE Transactions on Information Theory, 2007, 53(7): 2606-2610.

[4] DING C, FUJI-HARA R, FUJIWARAY et al. Sets of frequency hopping sequences: bounds and optimal constructions[J]. IEEE Transactions on Information Theory,2009, 55(7):3297-3304.

[5] KUMAR P V. Frequency-hopping code sequence designs having large linear span[J]. IEEE Transactions on Information Theory, 1988, 34(1):146-151.

[6] UDAYA P, SIDDIQI M U. Optimal large linear complexity frequency hopping patterns derived from polynomial residue class rings[J]. IEEE Transactions on Information Theory, 1998, 44(4): 1492-1503.

[7] CAO Z, GE G, MIAO Y. Combinatorial characterizations of one-coincidence frequency- hopping sequences[J]. Design Codes and Cryptography, 2006, 41(2): 177-184.

[8] CHU W, COLBOURN C J. Optimal frequency-hopping sequences via cyclotomy[J]. IEEE Transactions on Information Theory, 2005, 51(3):1139-1141.

[9] GE G, FUJI-HARA R, MIAO Y. Further combinatorial constructions for optimal frequency hopping sequences[J]. Journal of Combinatorial Theory Ser A, 2006, 113: 1699-1718.

[10] GE G, MIAO Y, YAO Z. Optimal frequency hopping sequences: autoand cross-correlation properties[J]. IEEE Transactions on Information Theory, 2009, 55(2): 867- 879.

[11] FUJI-HARA R, MIAO Y, MISHMA M. Optimal frequency hopping sequences: a combinatorial approach[J]. IEEE Transactions on Information Theory, 2004, 50(10): 2408- 2420.

[12] LEMPEL A, GREENBERGER H. Families of sequences with optimal Hamming correlation properties[J]. IEEE Transactions on Information Theory, 1974, 20(1): 90-94.

[13] PENG D, FAN P. Lower bounds on the Hamming auto- and crosscorrelations of frequency-hopping sequences[J]. IEEE Transactions on Information Theory, 2004, 50(9): 2149-2154.

[14] BERLEKAMP E. Algebraic Coding Theory[M]. New York: McGraw-Hill, 1968.

[15] LIDL R, NIEDERRERTER H. Finite Fields[M]. London: Addison-Wesley, 1983.

[16] WANG Q. Optimal sets of frequency hopping sequences with large linear spans[J]. IEEE Transactions on Information Theory, 2010, 56(4):1729-1736.

[17] BOGRART K, STEIN C, DRYSDALE R L. Discrete Mathematics for Computer Science[M]. College Publishing, 2005.

[18] 李超, 屈龙江. 密码学讲义[M]. 科学出版社, 2010.CHAO L, QU L J. Lectures on Cryptology[M]. Science Press, 2010.

[19] GOLOMB S W, GUANG G. Signal design for Good Correlation, for Wireless Communication, Cryptography, and Radar[M]. Cambridge Univ Press, 2005.

[20] 胡予濮, 张玉清, 肖国镇. 对称密码学[M]. 北京：机械工业出版社,2002.HU Y P, ZHANG Y Q, XIAO G Z. Symmetric Key Cryptography[M].Beijing: China Machine Press, 2002.