基于改进粒子群算法的二维相位解缠方法

张 妍 冯大政 曲小宁

（西安电子科技大学雷达信号处理国家重点实验室，陕西 西安710071）

引 言

干涉合成孔径雷达（InSAR）信号处理主要是通过两幅相干复图像所对应的像素点之间的绝对相位差来获取目标高度。但在实际中由于干涉相位图的相位差被限制在［－π，π］之间，丢失了2nπ的相位信息，所以如何从缠绕的相位中恢复目标的绝对相位是干涉合成孔径雷达信号处理的关键步骤。

干涉合成孔径雷达相位解缠的方法主要可以分为整体法和局部法。其中整体法是将相位解缠问题转化为求解数学最小范数极值问题，目前较多使用的方法是以最小二乘法为代表［1－2］的相位展开方法，该方法以展开相位梯度与缠绕相位梯度偏差最小为标准建立相应的数学模型，求解最接近于真实值的解缠相位。但由于此类方法每个像素点的解缠结果都为近似值，所以残差点引起的误差会扩散至整个图像中去，从而影响整体解缠精度。局部法是基于路径跟踪的相位解缠法，如Goldstein等人提出的"枝切法"［3］为代表的路径跟踪法就是局部法的一种。它通过识别干涉图中的正负残差点并在它们之间建立路径枝切线，积分时避开这些枝切线来实现相位解缠。该方法最大的优点是消除了因积分路径不同而出现的相位展开结果不一致的现象，避免了误差扩散到整个图像中去。但在残差点较多的区域，枝切线容易形成环路，从而导致部分区域无法解缠而形成"孤岛"。此外，网络流法［4］、利用干涉图像边缘检测的方法［5］、基于局部频率估计法［6］、多基线法［7－8］都被用于求解相位缠绕问题。

在枝切法中，枝切线的建立非常重要，枝切线的长度越短越有利于相位的展开，近年来在这方面提出了多种建立枝切线的优化方法［9－12］，而粒子群算法（PSO）［13］作为一种性能优良的优化算法同样也可以被用于求解最短枝切线问题。文章提出了一种基于粒子群算法的干涉合成孔径雷达相位解缠法，该方法利用粒子群算法求解连接干涉图中所有正负残差点的最短路径，以这条最短路径为枝切线进行相位解缠，同时在求解最短枝切线的过程中引入了类似遗传算法的"变异"算子，改进了粒子群算法在处理离散大规模问题上容易陷入局部收敛的缺陷。

1 改进粒子群理论的相位解缠

在采用枝切法进行相位展开的过程中，枝切线如何进行建立是非常关键的一步。而枝切线的设置原则为尽量选择距离较近的残差点进行连接，枝切线的长度越短，相位解缠的效果就越好。这是因为较短的枝切线在积分的过程中不但更容易被避开，还可以避免由于被长枝切线所包围形成无法解缠的闭合区域。由于这种求解路径最短的概念与图论中的旅行商问题（TSP）［14］非常相似，可以将残差点视为旅行商问题中的城市，而建立的枝切线则视为城市之间的连接线，它们之间的唯一不同之处在于旅行商问题需要计算从某一城市出发按照最优化原则逐一连接所有的城市的最短连路径，而枝切法需要匹配正负残差点然后进行连接，最后求出连接残差点的枝切线总体最短距离。

由于需要成对的连接正负残差点，所以正负残差点之间的距离之和可以表示为公式（1）的适应度为

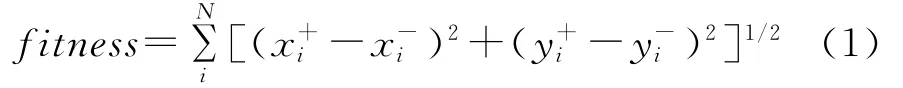
针对求解枝切线最短问题进行了类似旅行商问题的建模，分别用 “1”和“－1”两种极性标记干涉图中的正负残差点（在通常情况下干涉图中的正负残差点个数并不相等，也就是整体极性并不平衡，这就需要通过增加最靠近残差点的边界点作为极性相反的残差点进行极性平衡，使得整体的极性为0，即正负残差点的个数相等），然后连接所有残差点并通过粒子群算法对枝切线进行优化最终找到一条最短路径。

基本的粒子群算法是通过个体之间进行协作并分享全局的社会知识来达到优化效果的，优化公式如（2），（3）所示为

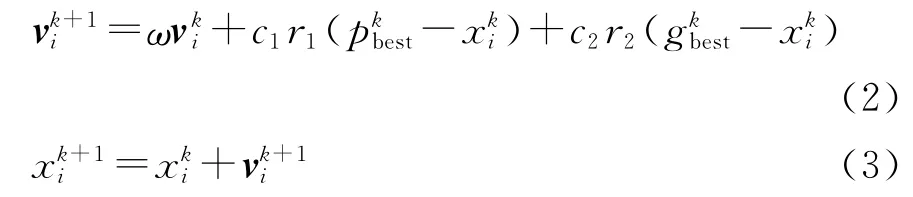
式中：pbest为粒子本身所能找到的最优解，称为个体极值；gbest为整个粒子种群目前找到的最优解，称为全局极值；是第i个粒子在第k次迭代中的速度向量；是第i个粒子在第k次迭代中粒子的位置；ω表示惯性权重，用来控制粒子原来的速度对当前速度的影响，一般取值为1；c1和c2为加速常数，用于调节全局最好粒子方向和个体最好粒子方向飞行的最大步长，其值的选取范围通常为（0，2）；r1和r2是［0，1］范围内的均匀随机数；k表示粒子更新的次数。

根据对英语词汇学习研究的内容进行分类，将所得文献分为了四类：学习方式研究、教学研究、综述研究和变量关系研究，四类研究的具体情况如表2。

虽然基本的粒子群算法具有建模简单、易操作、效率高等优点，但由于在很多实际问题的处理上都需要在离散空间进行建模，而Clerc在文献［15］中重新定义了粒子群算法中的加减法操作，同时引入了交换子和交换序的概念，并定义速度与随机数的数乘为随机数对应概率值保留速度中的所有交换子，实现了基本粒子群算法向离散空间的映射。重新定义后的粒子群状态更新公式如（4），（5）所示为

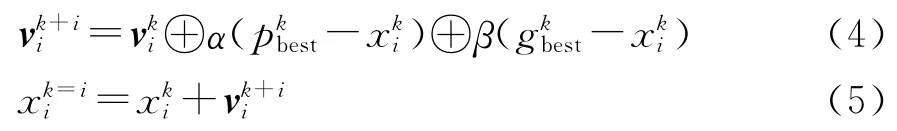
式中：α和β为学习系数，其值为［0，1］范围内的均匀随机数；α（－表示基本交换序 （－）中的所有交换子以α概率保留；β－）表示基本交换序－）中的所有交换子以概率β保留；⊕为两个交换序的合并算子。

在利用粒子群算法求解连接正负残差点的最短距离时，需要对正负残差点进行类似TSP问题的建模，可以假设一组残差点序列代表一种可能的解的话，就可以使用离散粒子群算法对其进行优化。在具体的建模过程中，首先，将所有的正负残差点进行编号，使正残差点的编号顺序固定不变，而负残差点则进行随机排序，编码如图1所示。

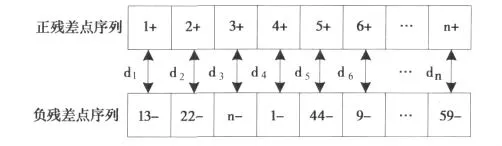
图1 正负残差点序列

图1中的d1、d2、……、dn为正负残差点之间的对应距离，这些距离之和就是需要优化的枝切线的总长度，也就是上文所提到的适应度。为了能够快速准确的得到连接正负残差点的枝切线的最短距离，将随机选取N个粒子代表不同顺序的负残差点序列。根据公式（4），在找到了个体极值和全局极值之后，比较当前位置与个体极值以及全局极值，并分别以α和β的概率进行保留，在计算出粒子的速度之后再根据公式（5）更新粒子的位置，也就是更新负残差点序列。在整个优化的过程中，始终以适应度持续变小为原则，通过一定次数的迭代计算（也就是初始种群根据基因算法不断的更新种群最后得到最优种群的计算过程）得到一个趋于收敛的全局极值gbest.

考虑到算法可能会陷于局部收敛，所以在整个算法优化的过程中引入遗传算法的变异算子（这里选用的是基本变异算子，以P＝0.9的概率进行变异）。在通过粒子群算法优化的过程中，可以对适应度较差的粒子进行变异，使粒子始终保持活性，防止算法陷入局部收敛。具体的算法流程如图2所示。

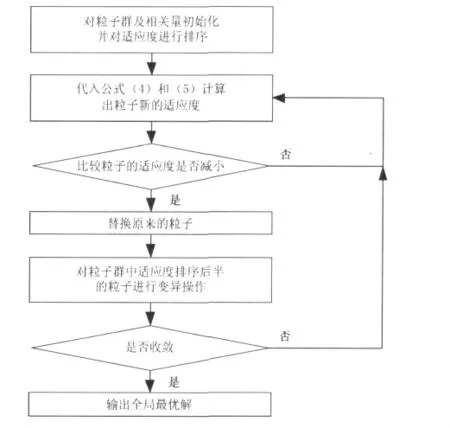
图2 算法流程图

步骤1：对粒子以及相关量进行初始化。根据公式（1）计算出粒子的初始适应度，再对所有粒子的适应度进行排序。

步骤3：对所有粒子的适应度进行排序。将适应度排序后半的粒子以概率P进行“变异”（通常选择0.9作为突变概率）。

步骤4：判断适应度是否收敛，如果均未收敛则进行新一轮的迭代。否则记录收敛后的适应度及对应的粒子。

通过一定次数的迭代，得到了全局最小适应度以及对应的粒子，其中全局最小适应度就是所需要求的最短枝切线之和，而对应的粒子即为负残差点序列，连接负残差点序列到正残差点序列就可以得到的枝切线，然后利用求得的枝切线进行相位展开。这种方法的策略是通过粒子群算法在整个相位图中建立最短长度枝切线，同时也考虑到了分割路径的极性平衡，因此由相位展开过程中的积分路径所引起的解缠误差会更小，同时也不会出现无法解缠的孤立区域，提高了相位展开精度。

2 实验结果及分析

2.1 仿真实验

模拟的相位由Matlab软件中peaks函数产生，未加噪声的原始相位如图3所示。

图3 原始相位曲面

模拟的过程中加入1视相干系数为0.9，分布在［－1.125 8，1.125 8］的均匀噪声。噪声标准差为0.5rad（方差为0.25rad2），图4（a）为缠绕相位曲面。图4（b）为残差点图，其中白点表示正残差点，黑点表示负残差点。图4（c）、（d）分别为采用Goldstein算法以及PSO算法设置的枝切线，图4（e）、（f）为不同枝切线下相位展开的结果。可以看出，在残差点密度较小的情况下两者都能很好的对缠绕相位进行展开，但由于Goldstein建立的枝切线存在环路，干涉图中有一小块区域相位未能展开。

加大噪声的强度，将噪声标准差增加为0.65rad（方差为0.422 5rad2），图5（a）、（b）分别为缠绕曲面和残差点分布图，可以看出，相对于图4，干涉图的条纹变得模糊，残差点的密度也大幅增加。图5（c）和（d）分别为采用Goldstein算法以及粒子群算法设置的枝切线。其中Goldstein算法建立的枝切线长度明显长于PSO方法，而图5（e）和（f）为两种方法的展开效果，分别显示了采用Goldstein算法和PSO方法进行相位展开后的结果，通过比较可以看出，由于残差点密集，Goldstein法建立的枝切线形成了大量的环路，造成相位解缠的效果非常差，而PSO方法解缠结果更接近于原始的相位图，明显好于Goldstein方法。表1为Goldstein方法和本文方法建立的枝切线与运算时间的比较结果，结果表明本文方法建立的枝切线长度更短，用时更省。

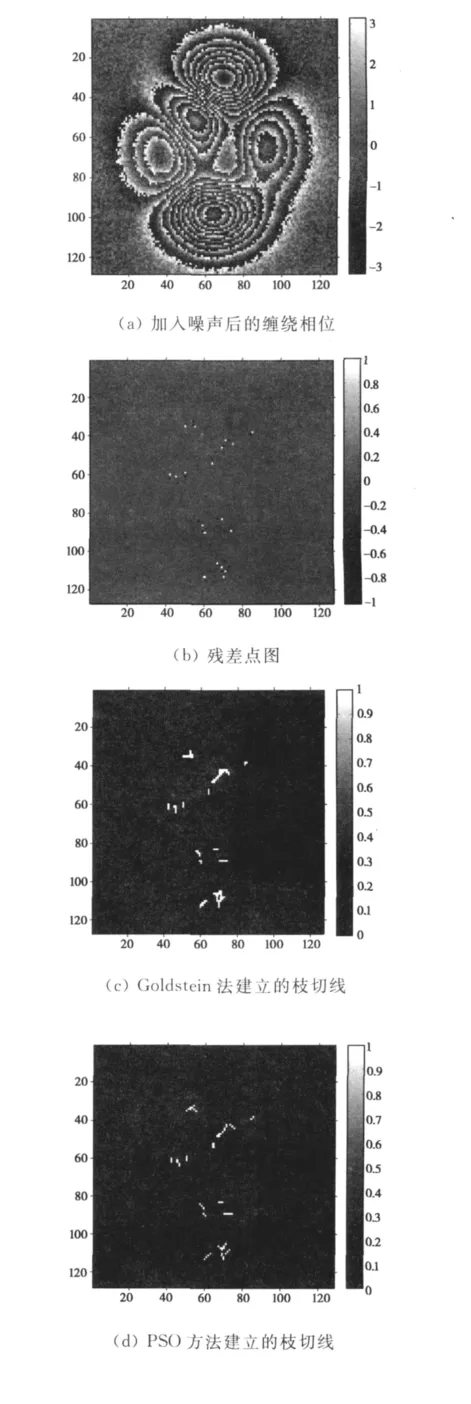
表1 不同方法建立枝切线长度和运算时间的比较（运算条件：Core2E4400 2.0G，2G内存）

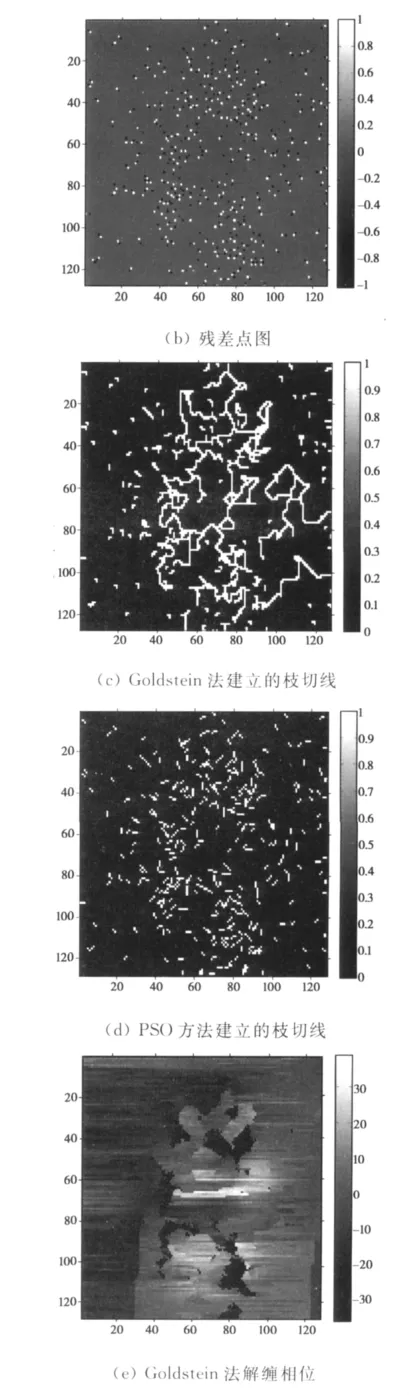
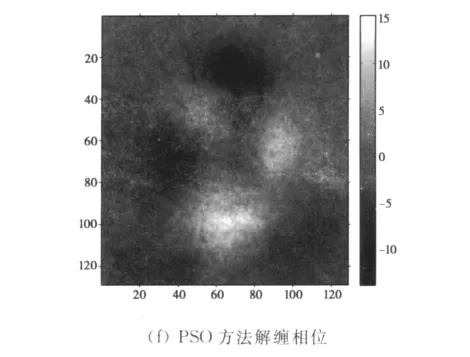
图5 噪声方差为0.422 5rad2下仿真实验结果

2.2 实测数据实验

实测数据为美国航天飞机SIR－C/X－SAR对意大利Etna火山观测录取的数据，干涉图大小为1 024×1 024，并经自适应方向窗滤波器［16－17］滤波。图6（a）为实测数据的干涉相位图，图6（b）为实测数据的残差点图，其中白点表示正残差点，黑点表示负残差点。通过比较图6（a）和（b）可知，干涉相位图中干涉条纹不清晰的区域表现在残差图上，即为残差点密集的区域。图6（c）和图6（d）分别为使用Goldstein方法和PSO方法建立的枝切线，可以看出使用Goldstein方法建立的枝切线不仅长度较长，且在残差点密集的地区形成了环路，而使用PSO方法所设置的枝切线比Goldstein算法设置的枝切线要短。

分别利用Goldstein枝切法、加权最小二乘法、质量图引导法和PSO法对实测数据缠绕相位图6（a）的缠绕相位进行相位展开，如图7所示。

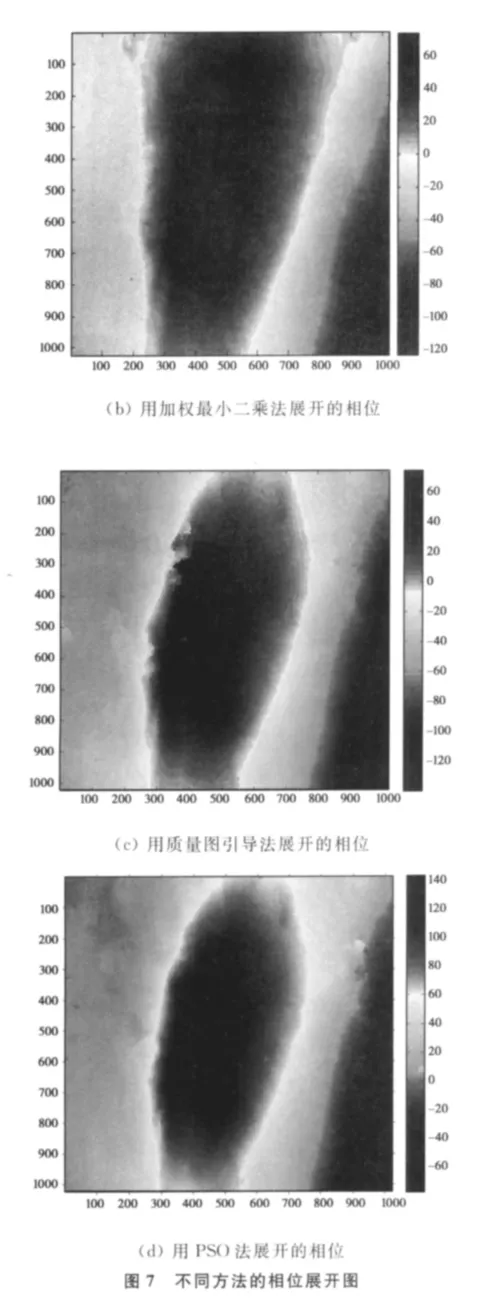
从图7可以看出，由于残差点密集区枝切线的连接形成了部分闭合区域，所以Goldstein法仅能获得局部解。但是在残差点稀疏的区域，展开的结果很好，同时抑制了误差在全局的传递。加权最小二乘法能够获取完整的解缠结果，即使在残差点密集的区域，也同样可以使用加权最小二乘法进行展开。但是从展开的图像中可以明显地看出，恢复出的绝对相位落差较小，所以利用加权最小二乘法进行展开时，误差在全局范围内传递，展开精度较低。质量图引导法整体展开效果较好，但在残差点密集的低质量区域展开的精度不够，相位出现跳变，而提出的方法展开效果要明显好于其他几种方法。

3 结 论

针对干涉合成孔径雷系统的二维相位展开问题进行了研究，提出了一种将粒子群算法应用到干涉合成孔径雷相位解缠中的方法，通过粒子群算法来求得最短的枝切线进行相位展开，同时针对粒子群算法容易陷入局部收敛的缺陷引入遗传算法的"变异"算子进行改进。仿真和实测数据解缠的结果证明了该算法相较于其他的相位展开方法具有更好的解缠精度，是一种有效的解缠算法。

［1］PRITT M D，SHIPMAN J S.Least－squares two－dimensional phase unwrapping using FFT′s［J］.IEEE Trans on Geoscience and Remote Sensing，1994，32（3）：706－708.

［2］FORNARO G，SANSOSTI E A.Two dimensional region growing least squares phase unwrapping algorithm for interferometric SAR［J］.processing.IEEE Trans on Geosci Remote Sensing，1999，37（5）：2215－2226.

［3］GOLDSTEIN R M，ZEBKER H A，WERNER C L.Satellite radar interferometry：two dimensional phase unwrapping［J］.Radio Science，1988，23（4）：713－720.

［4］COSTANTINI M.A novel phase unwrapping method based on network programming［J］.IEEE Trans on Geosci Remote Sensing，1998，36（3）：813－821

［5］付毓生，张晓玲，杨铁军，等.干涉合成孔径雷达边缘检测解相位模糊的方法［J］.电波科学学报，2003，18（1）：66－69.FU Yusheng ZHANG Xiaoling YANG Tiejun et al.Phase unwrapping with edge detection for interferometric SAR［J］.Chinese Journal of Radio Science，2003，18（1）：66－69.（in Chinese）

［6］SUO Zhiyong，LI Zhenfang，BAO Zheng.A new strategy to estimate local fringe frequencies for InSAR phase noise reduction［J］.IEEE Geoscience and Remote Sens－ing Letters，2010，7（4）：771－774.

［7］黄海风，王青松，张永胜.一种多基线相位解缠频域快速算法［J］.电波科学学报，2011，26（5）：831－836.HUANG Haifeng，WANG Qingsong，ZHANG Yongsheng.A fast phase unwrapping algorithm for Multibaseline interferometry in frequency domain［J］.Chinese Journal of Radio Science，2011，26（5）：831－836.（in Chinese）

［8］毛志杰，廖桂生，李 海.自适应图像配准多基线In－SAR干涉相位展开方法［J］.电波科学学报，2008，23（5）：877－882.MAO Zhijie，LIAO Guisheng，LI Hai.Multibaseline InSAR with image auto－coregistration for phase unwrapping［J］.Chinese Journal of Radio Science，2008，23（5）：877－882.（in Chinese）

［9］BIOUCAS－DIAS J M，VALADAO G.Phase unwrapping via graph cuts［J］.IEEE Trans on Image Processing，2007，16（3）：698－709.

［10］KAROUT S，GDEISAT M，BURTON D，et al.Two dimensional phase unwrapping using a hybrid genetic algorithm［J］.Applied Optics，2007，46（5）：730－743.

［11］魏志强，金亚秋.基于蚁群算法的InSAR相位解缠算法［J］.电子与信息学报，2008，30（3）：518－523.WEI Zhiqiang，JIN Yaqiu.InSAR phase unwrapping algorithm based on ant colony algorithm［J］.Journal of Electronics ＆Information Technology，2008，30（3）：518－523.（in Chinese）

［12］彭石宝，袁俊泉，向家彬.一种基于加权迭代贪婪算法的InSAR相位解缠的新方法［J］.电子与信息学报，2008，30（6）：1326－1330.PENG Shibao，YUAN Junquan，XIANG Jiabin.An improved InSAR phase unwrapping method based on iterative－weighted greedy algorithm［J］.Journal of E－lectronics ＆Information Technology，2008，30（6）：1326－1330.（in Chinese）

［13］CHEN Weineng，ZHANG Jun.A novel set－based particle swarm optimization method for discrete optimization problems［J］.IEEE Transactions on Evolutionary Computation，2010，14（2）：278－300.

［14］OBERLIN P，RATHINAM S，DARBHA S.Today＇s traveling salesman problem［J］.Robotics ＆ Automation Magazine，2010 17（4）：70－77.

［15］ZENG Hua，LIU Peng，SHEN Changpeng，et al.Discrete particle swarm optimization algorithm for weighted traveling salesman problem［C］//2010 8th World Congress on Intelligent Control and Automation（WCICA）.Jinan，July 7－9，2010：2008－2013.

［16］HUNTLEY J M.Noise－immune phase unwrapping algorithm［J］.Applied Optics，1989，28（15）：3268－3270.

［17］WU Nan，FENG Dazheng，LI Junxia.A locally adaptive filter of interferometric phase images［J］.IEEE Geoscience and Remote Sensing Letters，2006，3（1）：73－77.