重力坝稳定性尖点突变监控模型及软件模块研发

陈浙新，苏怀智，c，陈 兰

重力坝稳定性尖点突变监控模型及软件模块研发

陈浙新a，b，苏怀智a，b，c，陈 兰a，b

（河海大学a.水文水资源与水利工程科学国家重点实验室；b.水利水电学院；c.水资源高效利用与工程安全国家工程研究中心，南京 210098）

重力坝失稳宏观表现为从一种连续性状突然跳跃到不连续性状的突变现象。以突变理论作为研究突变现象的理论和方法，可以为重力坝稳定性分析和评价提供很好的手段和工具。借助坝工领域知识和突变理论，基于大坝安全变形监测资料，以大坝变形时效分量为大坝系统演化的状态变量，研究并构建了重力坝稳定性的尖点突变监控模型，并利用Delphi进行了软件模块的设计和研发，实现借助软件系统对重力坝稳定性的实时监控。

重力坝；稳定性监控；尖点突变模型；软件模块

1 研究背景

现代大坝安全管理的一项重要工作是借助大坝安全监控系统，对大坝施工和运行时的监测资料进行全面科学的管理，对大坝性态进行准确、高效的监控和评价，使大坝在安全运行的前提下，充分发挥工程效益［1－2］。重力坝在施工和运行过程中的稳定性是工程设计、建设、管理单位极其关注的工程问题，因而有必要研发一个监控重力坝稳定性的模块，使大坝安全监控系统能够对重力坝的稳定状况进行实时有效的监控。

传统的重力坝稳定性分析方法大致有以下几种：刚体极限平衡法、有限元等数值分析法、可靠度分析法、分项系数法和地质力学模型试验法等。大坝和坝基系统实际上是一个随着时间不断发展演化的动力系统，基于此，从动力系统的角度分析和评估工程稳定性成为近年来研究的一个热点领域。重力坝的失稳破坏，可能是产生滑动，也可能是发生倾倒滑移破坏，但不论是何种失稳方式，均是发生了明显的趋势性变形，而变形监测直观且真实地反映了大坝的运行状况，基于重力坝原型监测资料利用突变理论进行稳定分析已然是一种重要的手段［3－5］。

本文合理利用大坝原型监测资料，以重力坝测点顺河向水平位移的时效分量作为反映重力坝稳定状况的状态变量，建立了重力坝稳定性的尖点突变监控模型，并用Delphi进行了软件模块的研发，实现了借助软件系统对重力坝稳定的实时监控。

2 尖点突变模型

突变理论可用于研究和评估某系统从一种稳定状态到另一种稳定状态的跃进，其基本思想是利用势函数来研究系统的稳定状态，当系统处于稳定状态时，标志该系统状态的势函数取唯一的极小值，当系统处于不稳定状态时，势函数出现了多个极小值［6－7］。在初等突变类型中，尖点突变的几何直观性强，且临界曲面容易构造，应用最广，其平衡曲面和分叉集如图1所示。

图1 尖点突变的平衡曲面和分叉集Fig.1 Balance surface and bifurcation set of cusp catastrophe

若设想系统的状态是以x，u，v为坐标的三维空间的一个点来代表的，则该点必定总是位于平衡曲面上，其中，上叶和下叶对应于稳定平衡，而中叶对应于不稳定平衡。

尖点突变模型的势函数为

式中：x为状态变量；u和v为控制变量。

势函数的临界点是式（2）的解。

该方程给出了平衡曲面。实根的数目由判别式（3）决定，

Δ＝0构成分叉集。当Δ＞0或u＝v＝0时，方程只有1个三重实根，势函数只有1个临界点，系统状态是稳定的；当Δ＝0且u和v均非零时，方程有2个根，其中有1个是二重根，系统处于稳定状态与不稳定状态之间；当Δ＜0时，方程有3个不同的实根，势函数有2个极小值点，被一个极大值点隔开，系统处于不稳定状态。

3 重力坝稳定性尖点突变监控模型

重力坝测点顺河向位移的变化反映了重力坝的稳定状况。位移的3个组成部分中，水压分量（δH）和温度分量（δT）属弹性位移，而时效分量（δθ）作为包括坝体混凝土和基岩的徐变以及坝基的裂隙、节理和其它软弱构造等在荷载作用下发生的压缩和塑性变形的趋势性位移，其变化规律是反映大坝运行状态的重要表征，其突然增大或急剧变化是大坝或坝基病态工作的征兆。测点位移的时效分量是反映重力坝稳定状况的最为直观的效应量。本文以重力坝测点顺河向水平位移的时效分量作为反映重力坝稳定状况的状态变量，来建立重力坝稳定性的尖点突变监控模型。

由测点位移实测资料，根据其变化趋势，选择测点时效分量表示如下［4－5］：

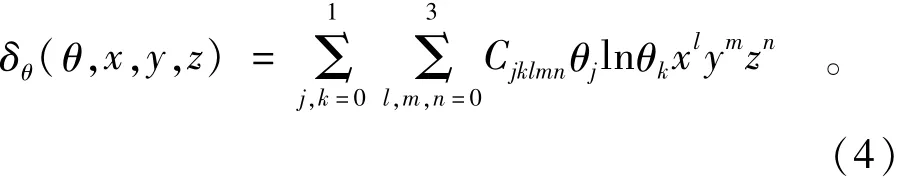
式中：θ为时效因子，取监测日至始测日的累计天数除以100所得的值；x，y，z为测点空间坐标。利用泰勒级数将式（4）按时效因子θ展开，则

式中ai（x，y，z）为展开系数，可由最小二乘法求出。

式中：

式（6）两边同除以b4（x，y，z），得到重力坝稳定性尖点突变监控模型的标准开折为

式（8）即为所建立的以测点时效位移为监测效应量的重力坝稳定性尖点突变监控模型。由突变理论，其稳定状态的判别式为

当Δ＞0或c2（x，y，z）＝c1（x，y，z）＝0时，重力坝处于稳定状态；当Δ＝0且c2（x，y，z），c1（x，y，z）均非零时，重力坝处于临界稳定状态；当Δ＜0时，重力坝处于不稳定状态。

4 软件模块设计与实现

为借助大坝安全监控系统实现对重力坝运行过程中稳定状况的实时监控，本文设计和研发了重力坝稳定性尖点突变监控模块，该模块主要实现以下功能：

（1）选择位移测点和导入监测数据，计算时效分量；

（2）显示测点的位移序列和过程线；

（3）实时判断稳定状况。

Delphi是一门面向对象的开发工具，可视化功能强，具有友好的图形界面，人机对话操作简单方便。采用Delphi作为开发工具，SQL Server作为后台数据库，根据上述功能需求，进行重力坝稳定性尖点突变监控模块设计。模块从大坝数据库中调用相关监测资料，进行稳定性分析判断。在数据库编程中，用到了连接组件TADOConnection、数据查询组件TADOQuery、数据源组件TDataSource和数据控制组件TDBComboBox，TDBGrid，TDBChat。稳定分析过程中的数据流程图如图2所示。

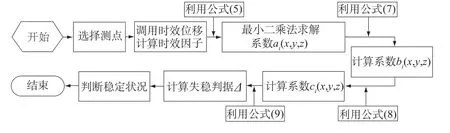
图2 数据流程图Fig.2 Data flow

本文设计的重力坝稳定性尖点突变监控模块操作简便、直观。模块界面如图3所示，包括“测点选择”、“位移序列表”、“位移过程线”和“分析结果”4个组成部分。软件模块连接某重力坝安全监测数据库，“测点选择”里的下拉式组合框中存储的项目是该重力坝所有的顺河向水平位移测点，具体应用时，首先根据大坝运行条件从中选择欲进行稳定分析的位移测点；则“位移序列表”中显示出所选位移测点的“监测时间”、“位移”和“时效分量”；“位移过程线”中显示出位移实测值和时效分量过程线图，以便查看。选择好位移测点后，点击按钮“稳定分析”，则开始如上节所述，对测点进行稳定分析和计算，求得失稳判据，判断重力坝的稳定状况。稳定分析结束后，“分析结果”中列出了“测点编号”、“测点名称”、“起始日期”、“结束日期”“判据”和“结果”。

图3 重力坝稳定性尖点突变监控模块界面Fig.3 Interface of the cusp catastrophemonitoring model of gravity dam stability

图3 中所选的PP12测点为一个以倒垂线法监测坝体水平位移的测点，测点所在高程为120 m，该测点所在坝段地质条件复杂，是整座大坝抗滑稳定的薄弱环节，故借助PP12测点的位移监测数据，对重力坝的抗滑稳定状态进行实时分析监控。以PP12测点从2002年11月27日到2008年12月31日的监测数据和由统计模型分离得到时效分量为基础，进行抗滑稳定分析。首先，根据最小二乘法，求出

代入公式（7）求得

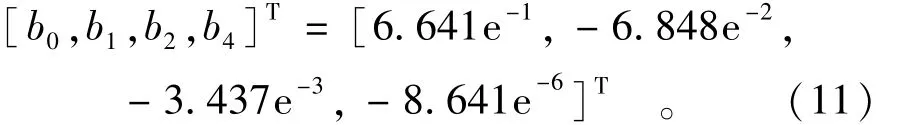
再求解c0，c1，c2得到该重力坝稳定性尖点突变监控模型的标准开折为

最后由公式（9）求得稳定性判据Δ＞0，表明重力坝处于稳定状态。

5 结 语

本文通过变形监测资料对重力坝稳定性作出分析和判断，认为大坝变形时效分量是反映重力坝稳定性的最为直观的监测效应量。依据坝工领域知识和突变理论，以大坝顺河向水平位移时效分量为大坝系统演化的状态变量，研究并构建了重力坝稳定性的尖点突变监控模型，并利用Delphi进行了软件模块的设计和研发。

借助文中介绍的重力坝稳定性尖点突变模型模块，随时间的推移，水平位移监测数据的更新，可实时快速地判别重力坝的抗滑稳定状态。

［1］ SU Huai-zhi，WEN Zhi-ping，WU Zhong-ru.Study on an Intelligent Inference Engine in Early-Warning System of Dam Health［J］.Water Resources Management，2011，25（6）：1545－1563.

［2］ 苏怀智，吴中如，戴会超.初探大坝安全智能融合监控体系［J］.水力发电学报，2005，24（1）：122－126.（SU Huai-zhi，WU Zhong-ru，DAIHui-chao.System of Theories and Methods Monitoring Intelligently Dam Safety［J］.Journal of Hydroelectric Engineering，2005，24（1）：122－126.（in Chinese））

［3］ 郭火元.突变理论及其在大坝稳定分析中的应用［J］.大坝观测与土工测试，1993，17（1）：10－13.（GUO Huo-yuan.Catastrophe Theory and the Application to Dam Stable Analysis［J］.Dam Observation and Geotechnical Tests，1993，17（1）：10－13.（in Chinese））

［4］ 汪亚超.混凝土重力坝抗滑稳定多维时空分析方法研

究［D］.南京：河海大学，2011.（WANG Ya-chao.Multi-dimensional Time-space Analysis Methods of Concrete Gravity Dam Anti-sliding Stability［D］.Nanjing：Hohai University，2011.（in Chinese））

［5］ 顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用［M］.南京：河海大学出版社，2006.（GU Chongshi，WU Zhong-ru.Safety Monitoring of Dams and Dam Foundations：Theories＆Methods and Their Application［M］.Nanjing：Hohai University Press，2006.（in Chinese））

［6］ 凌复华.突变理论及其应用［M］.上海：上海交通大学出版社，1987.（LING Fu-hua.Catastrophe Theory and the Application［M］.Shanghai：Shanghai Jiaotong University Press，1987.（in Chinese））

［7］ 何 平，赵子都.突变理论及其应用［M］.大连：大连理工大学出版社，1989.（HE Ping，ZHAO Zi-du.Catastrophe Theory and the Application［M］.Dalian：Dalian Jiaotong University Press，1989.（in Chinese） ）

（编辑：曾小汉）

A Cusp Catastrophe M onitoring M odel of Gravity Dam Stability and the Software M odule Development

CHEN Zhe-xin1，2，SU Huai-zhi1，2，3，CHEN Lan1，2
（1.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering，Hohai University，Nanjing，210098，China；2.College ofWater Conservancy and Hydropower Engineering，Hohai University，Nanjing，210098；3.National Engineering Research Center ofWater Resources Efficient Utilization and Engineering Safety，Hohai University，Nanjing 210098，China）

Macroscopic gravity dam instability ismanifested as a catastrophic phenomenon from a continuous to a discontinuous trait.As the theory and method to study the catastrophic phenomenon，catastrophe theory provided excellent approaches and tools for the stability analysis and evaluation of gravity dam.On the basis of dam safety deformation monitoring data，a cusp catastrophemonitoringmodel of gravity dam stability was established with the dam strain aging component as the state variable of dam system evolution.The softwaremodule was designed and developed with Delphi to achieve the real-timemonitoring of gravity dam stability.

gravity dam；stabilitymonitoring；cusp catastrophemodel；softwaremodule

TV698.1

A

1001－5485（2012）12－0058－04

10.3969／j.issn.1001－5485.2012.12.012 2012，29（12）：58－61

2011－10－20；

2011－11－28

国家自然科学基金（51179066，51139001）；新世纪优秀人才支持计划（NCET－10－0359）；国家重点实验室专项经费资助项目（2009586912，2009586012）；中央高校基本科研业务费专项资金资助（2010B01414）；江苏高校优势学科建设工程资助项目（水利工程）（YS11001）

陈浙新（1989－），女，浙江台州人，硕士研究生，研究方向为水工结构工程安全监控，（电话）025－83786128（电子信箱）chen＿zhexin＠126.com。

苏怀智（1973－），男，内蒙古鄂尔多斯人，教授，博士生导师，主要从事水工结构工程安全监控与服役寿命评估理论和方法的研究与教育工作，（电话）025－83786128（电子信箱）su＿huaizhi＠hhu.edu.cn。