倾斜岸坡角形域顶点排污浓度分布的实验研究

武周虎，吉爱国，胡德俊，时林艳，徐美娥

倾斜岸坡角形域顶点排污浓度分布的实验研究

武周虎a，吉爱国b，胡德俊a，时林艳b，徐美娥a

（青岛理工大学a.环境与市政工程学院；b.通信与电子工程学院，山东青岛 266033）

基于研制的倾斜岸坡角形域顶点排污立面二维扩散水槽实验装置及格栅振荡紊动系统，对8个倾角θ＝360°／β（角域映射系数β＝4，5，…，11）的角形域，按格栅振荡频率n＝20，40，60 r／min的3种情况进行了一系列瞬时线源排放的扩散实验，采用图像采集与数字图像处理技术测量二维浓度场分布。结果表明：各倾角的横向和垂向扩散系数均随格栅振荡频率的增大而增大，当格栅振荡频率n＝20，40，60 r／min时，各倾角横向扩散系数的平均值分别为18.38，30.88，43.94 cm2／s；垂向扩散系数的平均值分别为1.89，2.47，3.24 cm2／s；在格栅振荡条件下，垂向扩散系数平均占横向扩散系数的7.4%～10.3%，横向和垂向扩散系数随倾角的大小呈现波状变化特征。实验证明倾斜岸坡角形域顶点排污浓度分布呈现以角域映射系数β的奇偶不同和以β＝4的倍数的周期性变化规律。

环境水力学；倾斜岸坡；角形域；格栅振荡紊动；数字图像处理；浓度分布；实验研究

1 研究背景

江河水库岸坡通常是倾斜的，市政和工业排水多采用岸边侧向排放方式进入天然水体，并在岸边水域形成一定范围的超标水体，即污染混合区。针对不同水域排污浓度分布的研究是进行水环境功能区划分、优化削减负荷分配、制定水环境整治综合控制方案及设计污水排江排海工程的重要环节和关键技术［1－2］。河流水库横向（或侧向）与垂向扩散系数不相等是普遍存在的自然现象，在这种情况下倾斜岸坡角形域顶点排污在扇形空间的扩散和边界反射相当复杂［3－4］。开展角形域顶点排污浓度分布的实验研究，对于揭示横向与垂向扩散系数不相等条件下倾斜岸河库污染物浓度分布的变化规律及其应用，推动环境水力学的发展具有重要的理论价值和实际意义。

国内外以往的研究多集中在无限水域和矩形断面考虑边界反射情况下污染物浓度分布的解析解［5－6］、梯形渠道和倾斜岸地形各向同性扩散污染物浓度分布的理论解［7－8］，以及三峡库区岸边污染混合区的数值模拟［9－10］等方面。Holley等［11］研究了梯形渠道中的污染物岸边排放，给出横断面水深的变化对浓度分布的影响；李玲等［12］利用激光诱导技术（PLIF）量测了梯形明槽流动中的浓度分布，计算了污染物的横向扩散系数；武周虎等［3－4］采用镜像反射原理结合解析方法给出了倾斜岸河库横向与垂向扩散系数不相等情况下角形域顶点排污浓度分布的理论分析成果。笔者在横向与垂向扩散系数不相等的条件下，采用在矩形河渠验证过的地表水水质模型模拟了角形域中污染物的扩散过程，发现在倾斜边界上不能满足法向浓度梯度为零的物面条件，使本项实验研究显得更加重要。

本文基于研制的倾斜岸坡角形域顶点排污立面二维扩散水槽实验装置，在静止水体瞬时线源排放方式和格栅振荡紊动产生横向与垂向扩散系数不相等的水体环境条件下，对不同岸坡倾角开展角形域中污染物的扩散过程实验，采用图像采集与数字图像处理技术测量二维浓度场，进行实验结果与理论解的对比和扩散系数与振荡频率的关系分析。

2 实验装置与器材

立面二维扩散水槽实验装置主要包括：上部敞口的立面钢构架有机玻璃水槽（宽度y×高度z×厚度＝2 200 mm×2 100 mm×150 mm）、倾斜岸坡隔板、格栅振荡及变频调节系统、与水槽同厚度的坡底加药箱及控制插板、进水软管、底部放空管阀和背景灯箱等。该水槽为一套立面布置、格栅沿宽度y方向水平振荡（振幅110 mm）的yoz二维角形域水体紊动扩散系统，旨在模拟倾斜岸坡天然河库中某个截面上的污染物扩散过程，见图1。

图1 立面二维扩散水槽实验装置Fig.1 Experimental apparatus of vertical two-dimensional diffusion tank

振荡格栅采用直径2 mm钢丝编织成的14 mm正方形钢丝网，表面形成自然小波状编织面和焊接产生轻微变形扭曲（面），其外形厚度约为60～80 mm，利于带动水体横向紊动。格栅与滑轨驱动系统连接置于实验水槽内，伴随格栅的往复运动，在水槽中形成近似的横向与垂向异性紊动的扩散水体。控制插板将水槽左侧壁顶部加药箱与立面水槽分隔为暂时不连通的2个空间，当插板开启时药液迅速扩散进入立面水槽中，以便形成瞬时线源排放条件。为消除背景明暗不均现象对图像采集和处理造成影响，在水槽后面设置了背景灯箱均匀光源，尽量减少外界杂光的干扰。

实验器材主要有：电子天平、1 000 mL三角量杯、200 mL量筒、搅拌棒、钢卷尺、温度计、比色皿、秒表、照相机及三脚架等，采用罗丹名B示踪剂作为扩散物质。

3 实验方法与技术处理

3.1 实验方案与方法步骤

根据文献［4］给出的静止水体中倾斜岸坡角形域顶点排污浓度分布呈现出以角域映射系数β＝4的倍数的周期性变化规律，分别选择8个倾角θ＝ 360°／β（β＝4，5，…，11）的倾斜岸坡进行角形域水体紊动扩散过程实验，据此调整倾斜岸坡隔板倾角，加工安装不同规格的格栅，选择格栅振荡频率n＝20，40，60 r／min 3种情况。在相同条件下，扩散实验至少重复做1次，选取2次实验结果接近相同的进行分析。

3.1.1 实验方法步骤

（1）称取2.1 g罗丹名B放入三角量杯，加水至1 000 mL刻度线，搅拌，让其充分溶解1～2 h，使用时再搅拌均匀即可。

（2）实验水槽加水高出左侧壁倾斜岸坡角形域顶点加药箱前缘10～20 mm，关闭进、出水阀门，静置5～10 min。

（3）开启背景灯箱光源，调节格栅振荡频率至设定值，开启格栅振荡10～20 min，使水体达到均匀紊动。

（4）将1 000 mL初始浓度为2 100 mg／L的罗丹名B溶液倒入加药箱，开启控制插板按瞬时线源排放方式进行实验，计时秒表和浓度场测量图像采集同步开始。

（5）每隔15 s定时拍照一次，计时和浓度场测量图像采集到水槽右边界反射对浓度场产生明显影响为止，本次实验结束。

3.1.2 注意事项及说明

（1）开启插板要控制加药时间既不能太长，也不能给水槽内水体带来明显的初始动量，应通过前期试验掌握控制加药时间。

（2）实验前配制的罗丹名B溶液应与实验水槽中的水温接近，温差不要超过0.5℃。在实验中发现当罗丹名B溶液与实验水槽中的水温相差2℃时，就会产生明显的温差异重流，扩散云团就会因重力差作用沿倾斜岸坡潜入底部水体或因浮力作用沿表层水体扩散，这使得本来就复杂的倾斜岸坡角形域中的污染物扩散更具不确定性。这是天然河库岸边排污混合区范围，在水面上观察时漂浮不定的重要原因之一。

3.2 浓度场测量与标定

依据数字图像处理技术的工作原理，当罗丹名B浓度较大时颜色深，浓度较小时则颜色浅，这种浓度大小的变化就表现为颜色的深浅变化。在无探头接触影响的条件下，使用照相机采集扩散实验过程中的瞬时图像变化并记录，然后输入到计算机的数字图像处理系统中进行分析处理，再根据浓度－灰度的对应关系把灰度转化为浓度，最终污染物浓度扩散图像将以等浓度线图的形式显示。倾斜岸坡角形域顶点排污扩散水槽实验采用NikonD700照相机进行二维浓度场测量图像采集，立面水槽扩散实验与浓度场测量示意见图2。

图2 立面水槽扩散实验与浓度场测量示意Fig.2 Sketch of vertical diffusion tank experiment and concentration field measurement

在角形域水槽扩散实验开始前，在立面水槽正前方约4 m处架稳照相机，对准照相机镜头调好焦距。在开启加药箱控制插板排放扩散时开始计时，每隔15 s定时拍照一次至实验结束，然后将图片输入计算机，进行数字图像处理，最终获得二维浓度场等浓度线图。

为获取数字图像处理过程中的图片灰度与罗丹名B浓度之间的对应关系，进行如下标定实验。采用有机玻璃加工一个与立面水槽等厚度的比色皿（宽度×高度×厚度＝150 mm×225 mm×150 mm），分别配制8种不同浓度（0～280 mg／L）的罗丹名B标准溶液并在立面水槽格栅振荡和灯箱光源开启背景下，按浓度场测量图像采集方法拍照，之后将图片输入计算机，进行数字图像处理得到不同浓度相应的灰度值，据此得到浓度（C）－灰度（G）拟合曲线的标准方程为

C＝11 532／G－105.8 。（1）其中曲线拟合的相关系数达到R＝0.970。

3.3 数字图像处理技术

把数字图像处理技术应用于水中浓度场测量是环境水力学的一大进步，该技术经过有关学者的研究日渐成熟［13－14］。吉爱国等［15］在吸收已有成果的基础上，应用场论知识分析浓度场与灰度场的变化规律，借助于MATLAB平台对扩散实验过程中的瞬时图像进行处理，提出了本实验研究中的数字图像处理流程：首先对图像进行预处理，其次经滤波处理，再通过去除本底和二次滤波后，进而研究浓度场的特征，如图3所示。

图3 数字图像处理流程Fig.3 Procedure of digital image processing

对照相机在实验现场拍摄的图像进行预处理时，经实验比较分析选用Gamma矫正的效果很好；实验中使用非线性空间滤波器进行滤波是对其噪声干扰进行必要的处理；去除本底很大程度上解决了由于立面水槽扩散实验的特定条件，使图像采集过程中实验装置对研究对象产生的干扰。在颜色空间转换过程中，通过实验确定把RGB颜色空间转换成HSV颜色空间和HSI颜色空间，再对这2种方法进行比较，最终选择转换成HSV颜色空间模型描述红色水体污染物区域效果最好。因为HSV颜色空间比RGB颜色空间更接近于人们的经验和色彩的感知。由于浓度场是由水体的紊动产生，而紊动是由许多微小漩涡形成，所以水体扩散过程中存在类似于电磁场的矢量场。因此，将载有扩散时序信息的图像连续起来，就可以分析出灰度场的运动即浓度场的变化。据此研究实验图片中浓度场的特征，即对浓度场进行梯度、散度和旋度等分析讨论。结果表明：倾斜岸坡角形域顶点排污呈现浓度场梯度由源点沿径向下降的趋势，其梯度的下降快慢与极坐标数值有关；而浓度场散度大于零正好说明瞬时线源排放为正源散发通量；在角形域倾斜岸坡与振荡格栅斜边之间偶尔出现零星流体微团的浓度场旋度不为零，但角形域内水体总体处于无旋均匀紊动状态。因此本实验格栅振荡系统产生的扩散水体满足横向与垂向异性的均匀紊动条件。

4 结果与分析

4.1 扩散系数确定

在横向与垂向扩散系数不相等条件下，当角域映射系数β为偶数时，角形域顶点瞬时线源排污浓度分布的理论解为［3］

式中：M为线源排污强度；倾角θ＝360°／β，β为角域映射系数；n（n＝β／2）为自然数；Ey和Ez分别为横向和垂向扩散系数；C（y，z，t）为角形域内计算点（y，z）的扩散质浓度（定义域为：y≥0，y tanθ≥z≥0，下同）；t为时间。

当β为奇数时，角形域顶点瞬时线源排污浓度分布的理论解为［4］

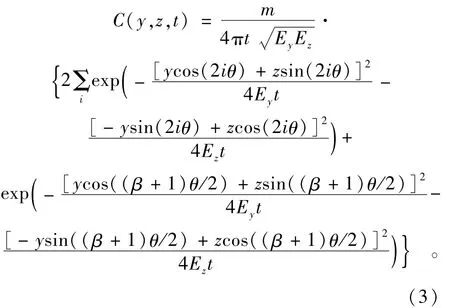
式中：当N＝INT（β／4）＝INT（β／4＋0.5）时（其中：INT（）函数为将数值向下取整为最接近的整数），i＝－N＋1，－N＋2，…，N；当N＝INT（β／4）≠INT（β／4＋0.5）时，i＝－N，－N＋1，…，N；其它符号同前。

在静止水体扩散实验水槽厚度为150 mm的倾斜岸坡角形域顶点中瞬时投放2.1 g罗丹名B，即相当于瞬时线源的排污强度M＝14 g／m，对8个倾角θ＝360°／β（β＝4，5，…，11）的角形域，按格栅振荡频率n＝20，40，60 r／min的3种情况和实验方法步骤进行一系列瞬时线源排放的扩散实验。

根据不同倾角和格栅振荡频率条件下实验过程中采集的图像资料，采用图像采集与数字图像处理技术依次获得相应条件下的实验等浓度线分布，导出实验过程中图像采集结束前一次的水面和某垂线上的浓度分布数据。假设一组横向和垂向扩散系数值，采用试算法，选择式（2）或式（3）计算水面和相应垂线上的试算（理论）浓度分布数据，分别绘制水面和垂线上浓度分布的实验曲线和试算曲线进行比对。当实验和试算曲线相差较大时进一步调整扩散系数，如此反复，直至水面和垂线上浓度分布的实验和试算曲线都能基本吻合时，相应的一组横向和垂向扩散系数值则为该组实验条件下的平均横向和垂向扩散系数，并采用相同实验条件下不同扩散时间的二维浓度场分布加以验证。图4给出了倾角θ＝60°，n＝60 r／min时横向和垂向扩散系数的其中3组试算比对曲线，图4中横向扩散系数的试算值分别为27，40，53 cm2／s；垂向扩散系数的试算值均为1.6 cm2／s。

图4 倾角θ＝60°，n＝60 r／m in时横向和垂向扩散系数的试算比对曲线Fig.4 Curves of transverse and vertical diffusion coefficients in the experiment and in three trial calculations（θ＝60°，n＝60 r／m in）

由图4可以看出，兼顾水面和垂线上浓度分布的实验和试算曲线都能基本吻合的条件，确定第二组试算结果，即实验倾角θ＝60°，n＝60 r／min时的平均横向扩散系数Ey＝40.0 cm2／s，平均垂向扩散系数Ez＝1.6 cm2／s。以此横向和垂向扩散系数计算倾角θ＝60°（β＝6），t＝60 s的理论等浓度线与实验等浓度线吻合良好，参见图6。

采用同样的方法可得到8个倾角、3种格栅振荡频率条件下，其它各组实验的横向和垂向扩散系数试算结果，并点绘于图5。

图5 不同振荡频率时扩散系数与倾角θ的关系曲线Fig.5 Diffusion coefficient vs.slopeθat different vibrating frequencies

由图5可以看出，各倾角的横向和垂向扩散系数均随格栅振荡频率的增大而增大，正好说明振荡频率越大，水体紊动强度越大从而引起扩散系数增大。当格栅振荡频率n＝20，40，60 r／min时，各倾角横向扩散系数的平均值分别为18.38，30.88，43.94 cm2／s，垂向扩散系数的平均值分别为1.89，2.47，3.24 cm2／s；垂向与横向扩散系数平均值的比值依次为0.103，0.080，0.074，即在格栅振荡条件下垂向扩散系数平均占横向扩散系数的7.4%～10.3%。

由图5还可以看出，横向和垂向扩散系数随倾角的大小呈现波状变化特征，在同一振荡频率下倾角θ＝90°和60°的横向和垂向扩散系数较小，而在倾角θ≤45°时横向和垂向扩散系数出现各异的波状变化特征。这一点可能受小倾角时水深变浅，格栅振荡紊动在倾斜岸坡底部产生的激波和不稳定漩涡引起垂向扩散系数增加所致。

4.2 实验结果与理论对比

根据倾斜岸坡角形域顶点排污立面二维扩散水槽实验过程中采集的图像资料，采用图像采集与数字图像处理技术获得相应条件下的实验等浓度线分布，即实验二维浓度场分布。图6（a）、图7（a）和图8（a）分别给出了倾角θ＝60°（β＝6），θ＝51.4°（β＝7）和θ＝45°（β＝8）、格栅振荡频率n＝60 r／min和扩散时间t＝60 s时的实验等浓度线分布，图6（b）、图7（b）和图8（b）分别为相应的理论等浓度线分布，其余略列。

图6 倾角θ＝60°（β＝6），t＝60 s的角形域等浓度线比较Fig.6 Comparison of concentration contours in angular field whenθ＝60°（β＝6），t＝60 s

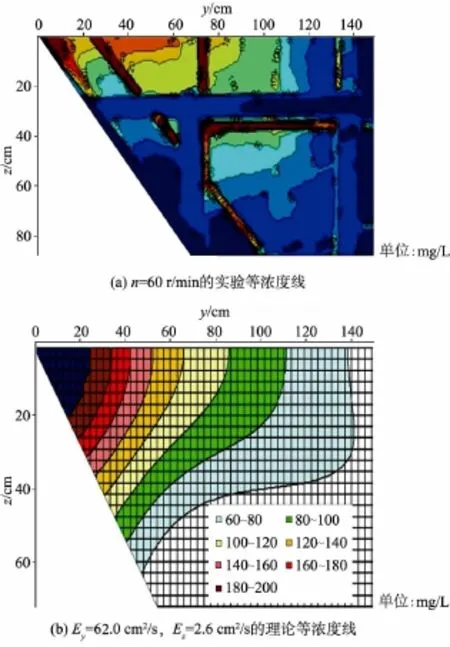
图7 倾角θ＝51.4°（β＝7），t＝60 s的角形域等浓度线比较Fig.7 Comparison of concentration contours in angular field whenθ＝51.4°（β＝7），t＝60 s

图8 倾角θ＝45°（β＝8），t＝60 s的角形域等浓度线比较Fig.8 Comparison of concentration contours in angular field whenθ＝45°（β＝8），t＝60 s

由文献［4］可知，在以角域映射系数β＝4的倍数的周期性变化规律中，β＝6，7和8分别为水面点污染物浓度的最小值、中间值和最大值点。由图6、图7和图8可以看出，根据β＝6，7和8时相应倾角θ＝60°，51.4°和45°边界反射的浓度叠加原理，当θ＝60°时污染物沿水面和倾斜岸坡上的扩散速度比角分线邻近区域上的要快，其浓度分布呈现以角分线为对称轴的分布特征；当θ＝51.4°和45°时污染物沿水面邻近区域上的扩散速度比倾斜岸坡邻近区域上的要快，其浓度分布呈现水面邻近区域上扩散较远的分布特征，倾角θ＝51.4°的等浓度线上最远与最近点的径向距离之差小于倾角θ＝45°的情形。虽然受实验装置框架遮挡图像干扰的影响，仍然可以看出其实验等浓度线与相应倾角理论解的浓度分布规律具有较好的一致性。

最后，对所有实验的等浓度线分布与相应条件下的理论等浓度线分布比较发现，倾斜岸坡角形域顶点排污浓度分布呈现以角域映射系数β的奇偶不同和以β＝4的倍数的周期性变化规律。再点绘所有实验的水面上y＝0.50 m处t＝120 s时浓度与倾角θ的关系曲线于图9。

图9 水面上y＝0.50 m处t＝120 s时浓度与倾角θ的关系曲线Fig.9 Concentration vs.slopeθat the location of y＝0.50 m above water when t＝120 s

由图9可以看出，在振荡频率和扩散时间都相同的条件下，倾斜岸坡角形域顶点排污水面上固定点的浓度呈现出以角域映射系数β＝4的倍数的周期性变化规律，上述结果与文献［4］的理论探讨结果完全一致。

5 结 论

（1）研制的倾斜岸坡角形域顶点排污立面二维扩散水槽实验装置及格栅振荡紊动系统，实现了在横向与垂向扩散系数不相等的水体环境条件下，较好地进行不同岸坡倾角的瞬时线源排放扩散实验。

（2）采用图像采集与数字图像处理技术，对立面二维扩散水槽实验中倾斜岸坡角形域顶点排污的二维浓度场分布进行测量，其结果可以较准确地反映真实情况。

（3）各倾角的横向和垂向扩散系数均随格栅振荡频率的增大而增大，横向和垂向扩散系数随倾角的大小呈现波状变化特征。在格栅振荡条件下，垂向扩散系数平均占横向扩散系数的7.4%～10.3%。

（4）实验证明倾斜岸坡角形域顶点排污浓度分布呈现以角域映射系数β的奇偶不同和以β＝4的倍数的周期性变化规律。

［1］ 周 丰，刘 永，黄 凯，等.流域水环境功能区划及其技术关键［J］.水科学进展，2007，18（2）：216－222.（ZHOU Feng，LIU Yong，HUANG Kai，et al.Water Environmental Function Zoning at Watershed Scale and Its Key Problems［J］.Advances inWater Science，2007，18（2）：216－222.（in Chinese））

［2］ 武周虎.倾斜岸水库污染混合区的理论分析及简化条件［J］.水动力学研究与进展（A辑），2009，24（3）：296－304.（WU Zhou-hu.Theoretical Analysis and Simplified Condition for PollutantMixing Zone in Reservoir of Gradient Bank［J］.Chinese Journal of Hydrodynamics，A，2009，24（3）：296－304.（in Chinese））

［3］ 武周虎.倾斜岸坡角形域顶点排污浓度分布的理论分析［J］.水利学报，2010，41（8）：997－1002，1008.（WU Zhou-hu.Analytical Solution to Concentration Distribution Discharged from the Intersection of Effluent into Corner Field of Inclined Banks［J］.Journal of Hydraulic Engineering，2010，41（8）：997－1002，1008.（in Chinese））

［4］ 武周虎，徐美娥，武桂芝.倾斜岸坡角形域顶点排污浓度分布规律探讨［J］.水力发电学报，2012，31（6）：166－172.（WU Zhou-hu，XUMei-e，WUGui-zhi.Regularity of Concentration Distribution Discharged from the Intersection of Effluent into Corner Field of Gradient Bank［J］.Journal of Hydroelectric Engineering，2012，31（6）：166－172.（in Chinese））

［5］ 武周虎，胡德俊，徐美娥.明渠混合污染物侧向和垂向扩散系数的计算方法及其应用［J］.长江科学院院报，2010，27（10）：23－29.（WU Zhou-hu，HU De-jun，XU Mei-e.Calculation Method of Lateral and Vertical Diffusion Coefficient for Mixed Pollutant in Open Channel Flow and Its Application［J］.Journal of Yangtze River Scientific Research Institute，2010，27（10）：23－29.（in Chinese））

［6］ FISCHER H B，IMBERGER J，LIST E J，et al.Mixing in Inland and CoastalWaters［M］.New York：Academic Press，1979，47－48.

［7］ 刘昭伟，陈永灿，王智勇，等.梯形渠道岸边排污浓度分布的理论分析［J］.环境科学学报，2007，27（2）：332－336.（LIU Zhao-wei，CHEN Yong-can，WANG Zhi-yong，et al.Analytical Solution to Concentration Distribution Discharged from a Stream of Effluent into Trapezoidal Channel Flow［J］.Acta Scientiae Circumstantiae，2007，27（2）：332－336.（in Chinese））

［8］ 武周虎.水库倾斜岸坡地形污染混合区的三维解析计算方法［J］.科技导报，2008，26（18）：30－34.（WU Zhou-hu.3-D Analytic ComputationalMethod of Pollutant Mixing Zone for Reservoir with Incline Bank［J］.Science＆Technology Review，2008，26（18）：30－34.（in Chinese））

［9］ 刘昭伟，陈永灿，付 健，等.三峡水库岸边排污的特性及数值模拟研究［J］.力学与实践，2006，29（1）：1－6.（LIU Zhao-wei，CHEN Yong-can，FU Jian，etal.Numerical Simulation of the Characteristics of Effluents in Three Gorges Reservoir［J］.Mechanics in Engineering，2006，29（1）：1－6.（in Chinese））

［10］HONG Yi-ping，ZHOU Xue-yi，CHEN Yong-can，et al.Computing Depth-Averaged Nonlinear k-εModel and Technique for Its Program Development［J］.Tsinghua Science and Technology，1999，4（1）：1371－1374.

［11］HOLLEY E R，SIEMOUS J，ABRAHAM G.Some Aspects of Analyzing Transverse Diffusion in Rivers［J］.Journal of Hydraulic Research，1972，10（1）：27－57.

［12］李 玲，李玉梁，陈嘉范.梯形断面水槽中横向扩散系数的实验［J］.清华大学学报：自然科学版，2003，43（8）：1124－1126，1152.（LI Ling，LIYu-liang，CHEN Jia-fan.Experimental Study on Transverse Diffusion Coefficients in an Open Trapezoidal Channel［J］.Journal of Tsinghua University（Science and Technology），2003，43（8）：1124－1126，1152.（in Chinese））

［13］晁兆波，赵文谦.数字图象处理技术在悬沙浓度测量中的应用［J］.四川联合大学学报（工程科学版），1997，1（1）：7－10.（CHAO Zhao-bo，ZHAOWen-qian.Application of the Digital Image Processing Technique to Measure the Concentration of Suspended Sediment［J］.Journal of Sichuan Union University（Engineering Science Edition），1997，1（1）：7－10.（in Chinese））

［14］黄文典，李 洪，李 嘉，等.数字图象处理技术测量浓度场的实验研究［J］.西南民族学院学报（自然科学版），2002，28（1）：97－101.（HUANGWen-dian，LI Hong，LIJia，et al.An Experimental Study of Application of Digital Image Processing Technique in Measurement of Concentration Field［J］.Journal of Southwest U-niversity for Nationalities（Natural Science Edition），2002，28（1）：97－101.（in Chinese））

［15］JIAi-guo，SHILin-yan，WU Zhou-hu.The Experimental Research of Pollutant Diffusion Based on Image Processing［J］.2011 2nd International Conference on Electronics and Information Engineering（ICEIE2011），Advanced Materials Research，2012，403－408：1993－1996.

（编辑：赵卫兵）

Experimental Research on Concentration Distribution of Pollutant Discharge into a Sloped-bank Angular Field from the Vertex

WU Zhou-hu1，JIAi-guo2，HU De-jun1，SHILin-yan2，XU Mei-e1
（1.School of Environmental and Municipal Engineering，Qingdao Technological University，Qingdao 266033，China；2.School of Communication and Electronic Engineering，Qingdao Technological University，Qingdao 266033，China）

Vertical two-dimensional sloped-bank diffusive tank and vibrating-grid turbulence generating system were set up for studies on the diffusion of instantaneous line-source discharging.The pollutant was discharged from the vertex of the domain with bank slope in eight cases ofθ＝360°／β（mapping coefficient of angular filed，β＝4，5，…，11）.The turbulence strength was controlled by three levels of grid vibration frequency n＝20，40，60 r／min.The two-dimensional concentration field distribution wasmeasured by image collection and digital image processing technology.The results showed that both the transverse and vertical diffusion coefficients were increasing with the growth of grid vibration frequency.The average transverse diffusion coefficientswere 18.38 cm2／s，30.88 cm2／s，

43.94 cm2／s，and the average vertical diffusion coefficients were 1.89 cm2／s，2.47 cm2／s，and 3.24 cm2／s respectively when the frequency was n＝20，40，60 r／min.The vertical diffusion coefficient was about 7.4%－10.3%of the transverse diffusion coefficient under grid vibration.Both the two coefficients showed undulating changeswith different slope angles.The experiment proves that the concentration of pollutant discharging from the vertex of angular field with sloped bank follows the pattern of periodic variation which depends on the odd／even parity ofβand themultiple ofβ＝4.

environmental hydraulics；sloped bank；angular field；vibrating-grid turbulence；digital image processing；distribution of concentration；experimental research

X143；X524

A

1001－5485（2012）12－0034－07

10.3969／j.issn.1001－5485.2012.12.008 2012，29（12）：34－40

2012－03－27；

2012－04－19

国家自然科学基金资助项目（50979036）

武周虎（1959－），男，陕西岐山人，教授，主要从事环境水力学与水污染评估研究，（电话）13061205508（电子信箱）wu＿zh2008＠yahoo.com.cn。