差分演化优化Ncut准则的彩色图像分割*

陈瑞南，刘秉瀚

（福州大学 数学与计算机科学学院，福建 福州350108）

基于图论的分割算法是近年来图像分割领域的研究热点[1-2]。基于图论的图像分割方法通过像素图像构造为带权无向图，通过将图像映射为加权的无向图，再把图像分割的问题转换成图的最优划分的问题。基于图论的分割准则[2]包括规范割Ncut(Normalize cut)准则和最小生成树MST(Minimum Spanning Tree)准则等，其中较为常用的是Ncut准则，其属于NP难问题。

使用Ncut准则存在两个难点：(1)当图像尺寸很大时,使用像素构造无向带权图将导致相似矩阵规模很大，内存消耗严重；(2)Ncut准则属于NP难问题，并没有精确求出Ncut最优解的算法。针对第一个问题出现了很多改进方法:有的方法先将图像划分为若干块区域，再使用Ncut方法进行分割，例如将分水岭算法与Ncut结合[3]；参考文献[4]将图像分为若干小块后每块使用Ncut方法进行分割之后对分割出的块再用Ncut方法进行分割。这些方法的目的都是通过减少图中的节点数从而缩减权值矩阵，以降低计算复杂度，提高算法效率。而对于第二个问题，在实际应用中常常采用近似的求解算法。Shi和Malik[1]提出的SM算法考虑了问题的连续放松形式，将原问题转换成求解相似矩阵或拉普拉斯矩阵的谱分解，通过求解广义特征方程,得到对图划分准则的逼近，但是SM算法求得的解也只是近似解。

针对使用Ncut准则图像分割的两个难点，参考文献[5]提出一种基于遗传算法优化Ncut准则的灰色图像分割算法。受此启发，本文提出一种基于Ncut方法的彩色图像分割算法：首先用爬山法对彩色图像进行初次分类，将像素聚类成c类，初次分类缩减了权值矩阵的规模；之后求出c类区域的相似矩阵，采用在求解NP-hard问题上具有更强寻优能力的二进制差分演化算法代替SM算法寻求最优Ncut值的图二分。实验结果表明，在同等预处理的条件下，本文的算法相比SM能够更精确地将目标分割出来。

1 背景知识

1.1 Ncut准则与SM算法[1]

一幅无向图G=(V;E)可以划分为两个不连接的顶点集C1和 C2。C1和 C2的不相似程度可以用如式(1)计算：

其中，权重w(u,v)表示节点u和v的相似性程度。图的最优二划分的目的是找到一个最小化cut(C1,C2)。然而,以式(1)为标准的分割方法存在偏向小区域的情形，如图1所示其容易划分出孤立点。

为了克服上述缺点，Shi和Malik提出了一种新的衡量相似性划分准则，即为正则化(Ncut)划分：

其中 assoc(C1,V)=Σu∈A,t∈Vw(u,v)表示顶点集 C1与 V 之间的连接边的权值总和。同理，assoc(C2,V)表示为顶点集C2与V之间连接边的权值总和。

求最优Ncut最优值是一个NP难问题,为此,Shi和Malik[1]将这一NP难问题转化为锐利问题（SM算法），从而求得有效的近似解。设N为顶点数总和，d(i)=Σjw(i,j)为节点i与其他顶点的连接权之和，D是d的对角矩阵；W为 N×N的对称矩阵且 W(i,j)=w(i,j)。则Ncut最小值的问题近似地转化为如下形式：

如果将y的取值放松至实数范围，式(3)的最优化问题相当于求解如下矩阵方程：

通过式(4)的第二小特征值对应的特征向量y=(y1,y2,…,yN)即为该问题的解。之后需要从y中取得一个分割值 yi将 顶 点 集 划 分 为 C1和 C2(C1={Vi｜yi＞0},C2={Vi｜yi≤0}))，通常取向量 yi=0或 y的中值。

1.2 二进制混合差分演化算法

差分演化算法(DE)是一种基于实数编码的具有保优思想的贪婪遗传算法。算法主要有变异、交叉和选择3个操作，由于这3个算子简单有效，使得DE比粒子群和遗传算法的收敛速度更快，全局收敛性能更优。贺毅朝等学者[6]通过引入了“辅助搜索空间”和“个体混合编码”等概念而提出了第一个二进制DE算法，并称之为二进制混合差分演化算法(HBDE)。HBDE已被证明完全收敛，具有DE所有的优点，非常适用于求解离散域上的最优化问题。

HBDE将个体混合编码为(X,B)，其中X是d维实数型搜索向量，B是d维二进制评价向量。设种群规模为NP，第t代中间种群中第i个中间个体的编码为(Xi(t),Bi(t)),其中:

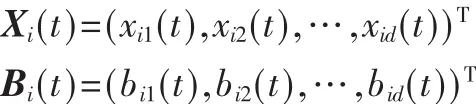
差异算子：

其中，p1≠p2≠p3≠i，1≤i≤NP,1≤j≤d,参数 F∈[0,2]为缩放因子，通常F=0.5是一个较好的初始值；r是[0,1]之间的随机数；CR∈[0,1]是交叉概率，大的 CR通常会加速收敛；R(i)是[1,n]上的一个随机整数用以保证至少有一个个体产生变异；Sig(x)=1/(1+e-x)。

选择算子：

其中 f(·)是个体评价函数。

2 优化Ncut准则的图像分割方法

以像素为单位构造权值矩阵再采用Ncut准则对图像进行分割，矩阵规模很大，耗时严重。为此本文提出一种解决策略，先用爬山法对彩色图像预先分成c类区域，之后采用彩色向量均值作为区域的描述向量。由于图像被压缩为c类，将c类一分为二的NP难最优化问题可采用二进制混合差分演化算法求得最优解。

2.1 基于爬山法的彩色图像初始化分割[7-8]

爬山法通过两个步骤在RGB色彩空间下将图像分割为具有较好一致性的数个图像区域。该方法首先求出整幅图像的三维RGB彩色直方图的局部极大值；然后将c个局部极大值作为聚类中心，通过k-means算法将图像聚类为c个一致性保持得较好区域。整个算法控制参数仅有每个通道的直方图柱数BinNum。

2.2 构造无向带权图

通过爬山法处理，图像I将划分为c类区域，即I=I1∪I2…∪Ic。将每一块的区域作为图G的节点。

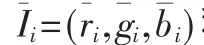
2.3 使用差分演化算法优化Ncut准则

以式(2)为评价函数，采用通过二进制差分演化算法将2.2节构造出的c类区域分为两类(C1和C2)的组合寻优算法，具体步骤如下：

(1)初始化种群。初始化HBDE的种群大小为NP，交叉概率为CR，缩放因子为F，辅助搜索空间为[-a,a]d。随机产生 NP个体，每个个体为(X,B)，其中 X=(x1,x2,…,xc)为实数编码对应于辅助空间，B=(b1,b2,…,bc)为对应的二进制编码。

(2)适应度函数的设计。采用式（2）的Ncut准则作为个体的适应值。

(3)评价个体。种群的单个个体对应的二进制编码B=(b1,b2,…,bc)的取为1和为0的基因分别代表图G的顶点属于C1和C2，查找权值矩阵 Wc求得个体对应的cut(C1,V)、和 cut(C1,C2)，之后通过式（2）求得个体的适应值。

(4)变异与选择。采用式(5)、(6)对种群的个体进行变异，采用式(7)进行选择操作。

(5)变异与选择是否达到指定的迭代次数tmax，若达到，则当前最优适应值个体对应的分类结果为最佳的分割效果，否则重复步骤(4)。

通过上述二进制差分演化算法迭代多次优化后得到的最优适应值个体所对应的个体Bbest即为使图最小化的分割。 将最优个体的二进制编码中为0和为1的区域分为两组C1和C2即可得到最终的图像二值化分割结果。

2.4 算法流程

综上所述，本文所提出基于HBDE优化的Ncut准则的图像分割算法整体流程为：

(1)采用爬山法将彩色图像聚为c类，从而使得图像I=I1∪I2…∪Ic。

(2)按照式(8)，用区域的彩色分量均值向量计算两两区域的相似性，从而构造出无向带权完全图Gc=(Vc,Wc)。

(3)使用二进制混合差分演化算法，迭代选择、变异操作多次到指定次数tmax，从而求得使Ncut准则最小化的图两类分割的最优个体。

(4)将最优个体对应的二进制编码的分类结果重新映射到原图像，使图像二值化。

3 实验结果及分析

本文的实验平台为Microsoft Windows XP professional、Matlab2010b，CPU 为 Intel Core 1.86 GHz,内存为2 GB，选取2幅来自公共数据集[9]的真彩色图像,分别采用本文算法和SM算法进行分割,效果如图2、图3所示。实验中的参数为：爬山法的参数BinNum=20；经过多次实验,相似性计算式(8)中的参数σ=5;差分演化算法种群大小 NP=10 c,采用 DE/r/1/bin模式,辅助空间向量 a=5，最大迭代次数tmax=200;SM算法的分割值取yi=0。

为了对比二进制差分演化优化最小化Ncut准则与SM算法的分割效果，现将实验结果分析如下：

(1)船。由于水波的色彩与船身相近，SM算法在水面波纹方面过分割，对比SM算法，本文算法能够更为清晰地的分割出船身。

(2)鹦鹉。背景的4个外角偏暗，使用SM算法受此干扰使得背景欠分割。采用本文的算法能够较为准确地分割出鹦鹉的整体，效果优于SM算法。

从表1的Ncut值可以看出，二进制差分演化算法比SM算法有更好的寻优能力。SM算法采用近似解法难免出现分割效果不佳的情况，二进制差分演化算法有较强的寻优能力因而能够找到更为理想的分割解。表1亦可使用差分演化算法寻优,运行时间略多于SM算法。

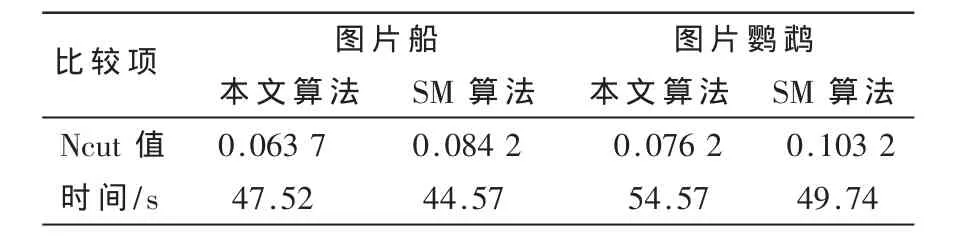
表1 两种分割算法的得到的时间对比

实验结果表明，采用本文的二进制差分演化优化Ncut准则的彩色图像分割算法相比SM算法在运行时间略高的情况下能够得到有更为精确的分割出目标。

[1]Shi Jiaobo， MALIK J.Normalized cuts and image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(8)：888-905.

[2]SOUNDARARAJAN P,SARKAR S.Analysis of mincut,average cut and normalized cut measures[C].Proceedings of the 3rd Workshop on Perceptual Organization in Computer Vision.Vancouver，Canada，2001：1-4.

[3]冯林,孙焘，吴振宇，等.基于分水岭变换和图论的图像分割方法[J].仪器仪表学报，2008，29(3):649-653.

[4]TUNG F,WONG A.Enabling scalable spectral clustering for image segmentation[J].Pattern Recognition，2010(43):4069-4076.

[5]翟艳鹏，郭敏,马苗，等.遗传算法优化归一化划分准则的图像分割[J].计算机工程与应用，2010,46(33):148-150，157.

[6]贺朝毅,王熙照，冠应展，等.一种具有混合编码的二进制差分演化算法[J].计算机研究与发展，2007，44(9):1476-1484.

[7]OHASHI T,AGHBARI Z,MAKINOUCHI A.Hill-climbing algorithm for efficient color-based image segmentation[C].IASTED International Conference on Signal Processing,Pattern Recognition,and Applications(SPPRA 2003),2003:17-22.

[8]ACHANTA R,ESTRADA F,WILS P,et al.Salient region detection and segmentation[C].International Conference on Computer Vision Systems(ICVS 2008),2008:66-75.

[9]MARTIN D,FOWLKES C,MALIK D T J.A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C].Proceedings of IEEE International Conference on Computer Vision,2001,1(2):416-423.