SVR在信号传递合约模型Ⅱ量化分析中的应用
张振锋
(盐城纺织职业技术学院,江苏 盐城224005)
激励合约优化模型的研究一般采用解析的、定性的方法进行分析[1]。但这种分析方法不仅导致激励合约优化模型在实际应用受到限制,也使得理论本身的发展受到限制。其原因主要有两方面,其一是模型所包含的效用函数难以用解析函数定量表达,造成整个模型难以作定量分析;其二是解析分析方法在对具有效用函数求导的梯度法的优化模型求解时难以施展。由于支持向量回归机在各领域得到成功的应用[2],所以用支持向量回归机对效用函数建模,解决信号传递优化模型的量化表达问题,进而对信号传递优化模型作量化分析。
本文研究用SVR解决信号传递优化模型Ⅱ的定量表达和分析问题,并与已有的解析分析方法相结合,利用SVR对效用函数进行建模,从而解决效用函数的表达问题。同时利用梯度法求解优化模型,从而解决传统解析方法无法解决的优化模型的量化分析问题。在用支持向量回归机对效用函数建模的基础上,本文推导出了提供生产率高、工作繁重的合约和提供生产率低、工作轻松的合约的委托人通过其设计的合约向代理人传递信息的信号传递模型的梯度表达式,并给出了相应的梯度法迭代算法。利用这一算法进行数值计算和量化分析,观察上述信号传递模型中参数变化对合约均衡点变化趋势的影响。
1 SVR与效用函数建模[3]
解决效用函数的定量描述问题是对激励合约优化模型定量计算的关键。而用SVR对效用函数建模又是解决效用函数的定量描述问题的关键。
1.1 支持向量回归机SVR
对小样本点集回归得到其隐含的函数关系的方法较多,目前比较成功的方法是利用支持向量回归机SVR。考虑用线性函数 f(x)=〈w,x〉+b逼近样本数据集 D={(x1,y1),…,(xl,yl)}(x∈Rn,y∈R)的问题。 从结构风险最小化思想出发,则其最优回归函数的优化模型为:
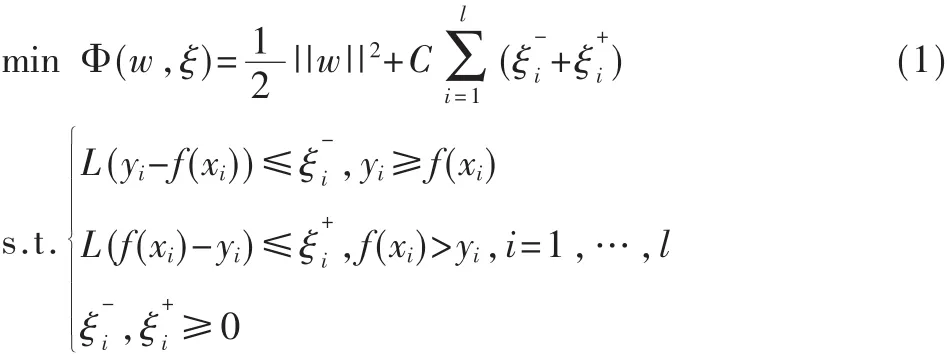
1.2 效用函数的SVR建模
效用函数在经济学中指消费者在消费某种商品过程中所得到的满足感。在激励合约中指对获取收益的满足感。效用函数带有很强的主观色彩,实际中由小样本点集隐含。本文利用SVR对效用函数建模作量化描述,即用SVR表达效用函数。首先利用所收集到的效用函数的样本集训练SVR,使其得到有关知识,这实际上是样本点隐含的函数关系在各个神经元上的权值。在SVR得到这组权值之后,就可以用来表达由样本点隐含的函数关系,即对于所给定的自变量,可以通过训练后的SVR定量确定效用函数的值。在用SVR表达效用函数的基础上,可以进一步定量计算相关的积分和导数。激励合约研究的是签约双方同为风险规避类型(至少是风险中性)的效用函数的情形。当效用函数是风险中性时,用一线性函数即可表达;而当取效用函数为风险规避类型时,可以用SVR来表达。用SVR表达的效用函数的基本表达式为:

其中svr(x)的曲线形状如图1所示(通过对实际样本点的训练回归而得)。仿真时,可以在效用函数的基本表达式中引入两个参数a和b,使效用函数具有如下形式:u(x)=af(bx),通过调节a和b即可对效用函数进行微调。
2 信号传递优化模型Ⅱ及其梯度法求解[5]
2.1 信号传递优化模型Ⅱ[1]
激励合约的信号传递优化模型Ⅱ可以形式化地表示为约束最值问题。典型的信号传递激励合约模型Ⅱ是:委托人达到效用最大化时,委托人通过激励合约向代理人传递其特征信号的优化模型。其求解的实际含义是指,提供生产率低、工作轻松的合约(wl,el)的 l型委托人和提供生产率高、工作繁重的合约(wk,ek)的 k型委托人分别设计合约,l型委托人通过合约向代理人传递特征信息以使代理人选择其设计的合约,k型委托人不需要向代理人传递信息便能使代理人选择其设计的合约。模型Ⅱ要解决的问题是,在代理人不知委托人是l型还是k型的情况下,l型委托人应该如何设计合约向代理人传递信息,以使得不情愿努力的代理人选择生产率低、工作轻松的合约(wl,el),同时使得委托人预期效用最大。

模型Ⅱ由式(3)~式(5)组成:k型委托人、l型委托人的合约模型:

调整后l型委托人的合约模型:

其中:k为生产效率,在模型中,k值相对小时,为 l型委托人模型,k值相对较大时,为k型委托人模型;wk、wl、ek、el分别为代理人选择合约(wk,ek)和(wl,el)所获得的工资和所付出的努力程度;∏(ek)、∏(el)分别为提供合约(wk,ek)的 k型委托人和提供合约(wl,el)的 l型委托人所获得的收益;ek*、wk*分别为k型委托人所求得的努力和所支付给代理人的工资;u(·)是代理人对于工资收入的效用函数;v(·)是代理人关于付出努力的效用函数,为线性函数;U是代理人的某个预定效用值。
2.2 信号传递优化模型Ⅱ的梯度法求解[5]
2.2.1 目标函数最值的梯度法求解
函数的梯度方向是函数值变化最快的方向,梯度法就是以函数的梯度方向作为极值点的搜索方向。当利用梯度法求函数的最小值时,要将函数的负梯度方向作为极值点的搜索方向。而当利用梯度法求函数的最大值时,则要以函数的正梯度方向作为极值点的搜索方向。算法如下:
输入:目标函数 f(X),其中 X=[wkek]T,[wlel]T,初始点 X1∈En(n 维欧式空间),步长 λ,允许误差 ε>0。
输出:使目标函数f(X)最大的解X*。
(2)若 |Δf(Xm)|>ε, 则 执 行 Xm+1←Xm+λ▽f(Xm),m←m+1,转步骤(1);
(3)此时 Xm就是所求的最优解 X*,f(Xm)就是目标函数的最大值,算法结束。
2.2.2 障碍函数的构造[5]
用梯度法求解信号传递优化模型Ⅱ,要将约束条件下的最值问题转化为非约束条件下的最值问题。一般做法是构造障碍函数,即用若干障碍项表示相应的约束条件,并将这些障碍项加到目标函数中。当可以保证障碍项函数的初始值大于0时,选用log函数为障碍项函数,否则选用式(6)为障碍项函数。

式(6)是本文设计的障碍项函数,式(7)是其导数。如此设计的优点是使障碍项函数在0点有连续的导数,以避免迭代过程在0点处出现振荡;缺点是约束条件可能得不到绝对满足。
2.2.3 概率函数q(t)的构造
[1]中q(t)是阶跃函数,其导数不存在。为了能使用梯度法,用式(6)替代阶跃函数,其导数存在。用式(9)中的函数可以代替参考文献[1]中的阶跃函数。
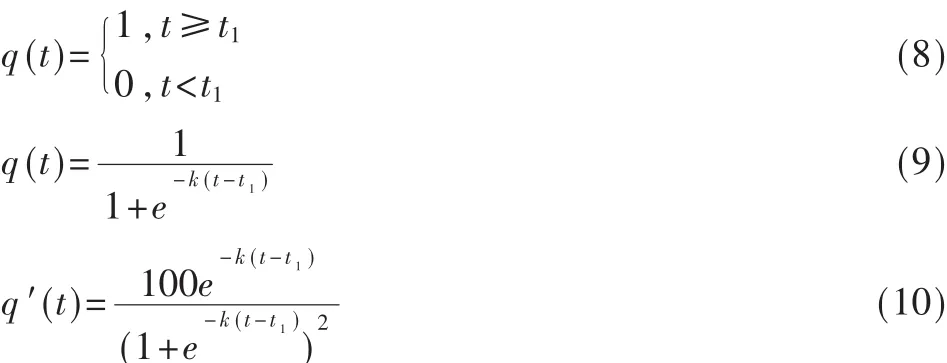
2.2.4 信号传递模型Ⅱ的梯度法求解的梯度公式
信号传递合约模型Ⅱ带有障碍项的目标函数为:
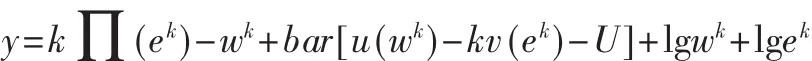
对于k型、l型委托人的模型:
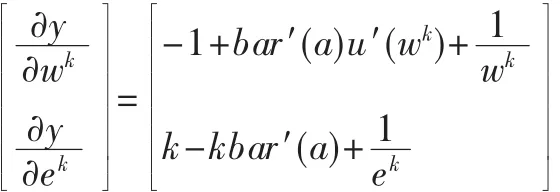
其中 a=u(wk)-kv(ek)-U,∏(ek)=ek,v(ek)=ek。
对于l型委托人向代理人发送信息的模型:

其中∏(ek*)=ek*,∏(el)=el。
由于在设计障碍函数时,保证了障碍项有连续一阶导数;通过选择合理的SVR参数,使得用SVR建模的效用函数也有一阶连续导数,从而使整个目标函数有一阶连续偏导数,满足梯度法的应用条件。通过实验选择合理的步长λ和精度ε,可以使算法收敛并有较快的收敛速度。另外所要求解的向量X维数为3或2,即问题的规模为3或2,则算法的时间和空间复杂度分析可以忽略。这些都保证了上述梯度法的有效性。
3 计算结果与分析
3.1 量化计算的目的与步骤
量化计算的目的,是观察模型参数变化对合约均衡点变化趋势的影响。对于该模型,主要观察:在其他参数不变的情况下,委托人的生产效率k值的变化在信息对称情况下对合约均衡点的影响,及l型委托人的合约均衡点的设置变化。
量化计算的步骤:
(1)量化计算的关键是对效用函数建模。所以第一步是用SVR对经过调查的效用函数样本点训练建模。量化计算中,效用函数u(·)取式(2)的定义,即为风险规避的,v(·)取线性函数,v′(·)=1,即为风险中性的。 样本点和建模的结果如图1所示。
(2)对于该模型,在梯度法算法中,输入初始值X=[wkek]=[wlel]=[1 1],迭代步长 λ=0.000 01,终止误差ε=0.1。
对式(3)和式(4)的委托人模型,令式(3)中的生产效率 k值从 0.1,0.2,…,0.6增大时,反复调用上述梯度法计算目标函数值,得到如图2星号线所示的委托人的生产效率k值的变化对合约均衡点的影响,其中均衡点对变化方向已在图2中标出;对式(5)的合约模型,令式(3)和式(4)中k值较小时的模型为l型委托人(提供生产率低、工作轻松的合约)模型,k值较大时的模型为k型委托人(提供生产率高、工作繁重的合约)模型,反复调用上述梯度法计算目标函数值,得到如图2加号线所示的委托人的生产效率k值较小的l型委托人的的合约均衡点的变化,其中均衡点对变化方向已在图2中标出。

3.2 结果及其分析
图2是本文中信号传递合约模型的量化计算结果。横轴表示代理人的工资水平,纵轴表示代理人努力程度,星号点是l型委托人和k型委托人合约均衡点,加号点是经调整后l型委托人设计的合约均衡点。
图2的结果表明,在其他参数不变的情况下,随着委托人的生产效率k值的增加,即由k值较小时的l型委托人到 k值较大时的 k型委托人,均衡点(w,e)向右下方向移动;这表明了l委托人所付给代理人的工资低于k型委托人所付给代理人的工资,而l型委托人所需要代理人的努力程度却高于k型委托人所需代理人的努力程度,这显然是不合理的,从而必须对l型委托人设计的合约进行调整,使l型委托人向代理人传递其特征信息,调整到图2的加号线所示,以便使代理人明白l型委托人设计的合约要求的努力程度低于k型委托人所需代理人的努力程度ek,而支付的工资也低于k型委托人支付给代理人的工资wk。这一结果提示委托人,当委托人提供生产率低、工作轻松的合约时,要向代理人传递其工作轻松、要求努力程度低的信号才能使不情愿努力的代理人接受l型委托人设计的合约。
本文在利用SVR对效用函数建模的基础上,用梯度法量化求解信号传递优化模型,对信号传递模型Ⅱ(委托人通过激励合约向代理人传递其能提供生产率低、工作轻松的合约(wl,el)特征信号的优化模型)进行了定量计算和分析。由于定量计算数值结果的直观和易于理解,容易发现解析分析难以得到的信息。经完善后也可以用于指导含有信号传递合约优化模型Ⅱ的实际委托-代理合约的设计。
参考文献
[1]因内思·马可—斯达德勒,J.大卫·佩雷斯—卡斯特里罗,著.信息经济学引论:激励与合约[M].管毅平,译.上海:上海财经大学出版社,2004.
[2]CHEKMAREV D,KHOLODOVYCH V,KORTAGERE S,et al.Predicting inhibitors of acetylcholinesterase by regression and classification machine learning approaches with combinations of molecular descriptors[J].Pharmaceutical Research,2009,26(9):2216-2224.
[3]Wang Shitong,Zhu Jiagang,CHUNG F L,et al.Theoretically optimal parameter choices for support vector regression machines Huber-SVR and Norm_r-SVR with noisy input[J].Soft Computing.2005,9(10):732-741.
[4]朱嘉钢,王士同,杨静宇.鲁棒的 r-支持向量回归机中参数 r的选择研究[J].控制与决策,2004,19(12):1383-1386.
[5]张振锋,朱嘉钢.支持向量回归机在逆向选择合约模型量化分析中的应用[J].计算机应用,2010,30(3):779-788.

