类电磁机制算法的应用研究
段熙鹏,蔡延光,汤雅连
(广东工业大学 自动化学院,广东 广州510006)
类电磁机制 EM(Electromagnetism-like Mechanism)算法是一种新型的基于种群的随机全局优化算法,在现实生活中具有很强的应用背景,可以应用到分子生物、调度安排、工程设计等领域。近几年来已有不少学者做了相关研究[1-4],并取得了很好的成果。但是对于关联运输调度问题 RVRP(Related Vehicle Routing Problem)的探讨在国内还不多见。但是前人研究的各种车辆路径问题VRP(Vehicle Routing Problem)对本文的研究有很重要的借鉴意义。本文主要研究在载重约束下,对各车场中的多种不同类型车辆及配送路线进行合理安排,在满足所有客户要求的前提下,使配送成本最低。
1 问题描述及数学模型的建立
1.1 问题描述
多车场多车型关联运输调度问题可以简单描述为:假设给定车场信息以及客户信息(位置和货物需求量等)、货物之间的关联系数、不同类型车辆信息(载重约束、里程约束和关联约束等),要求合理安排车辆和运输路线,在满足所有客户需求的前提下,使配送成本最低。
1.2 数学模型

假设客户编号为 1,2,…,l,车场编号为 l+1,l+2,…,l+N。定义变量如下:


2 改进的EMA
2.1 传统EMA基本原理
EMA是一种随机全局优化算法。它模拟电磁场中的吸引和排斥机制,将每个解比作一个带电粒子,然后按一定的准则使得搜索粒子朝最优解移动。由于此思想与电磁理论中吸引与排斥机制有相似性,但也存在差异性,所以称之为类电磁机制。该算法的收敛性已经得到证明,当迭代次数趋于极限时,种群中至少有一个粒子以概率1移动到全局最优附近。
根据电磁理论中的吸引——排斥机制,EMA把每个搜索粒子想象成空间中的一个带电粒子,每个粒子的电荷由待优化的目标函数的函数值决定。该电荷也决定了该粒子对其他粒子的吸引或排斥的强弱。目标函数值越优,寻优越强。通过计算其他粒子与当前粒子的合力来确定每个粒子下一步的走向。
2.2 算法流程
为不失一般性,考虑极小值的优化问题,如式(12)所示。f(x)为目标函数,x为决策向量。
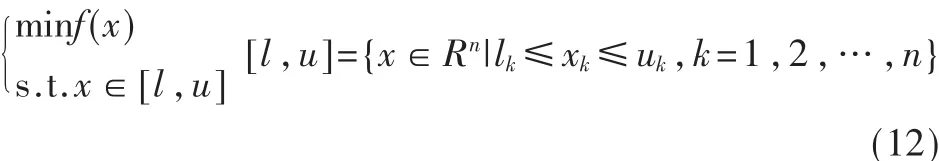
算法流程如下所述:
(1)初始化
初始化就是从已知可行域中随机取一定数量的点,然后对这些点进行进一步搜索,计算每个粒子的目标函数值,并将目标函数值最优的粒子记为xbest。
(2)局部搜索
局部搜索针对单个粒子,用来改进种群中已搜索到的解。它为种群的全局搜索提供了有效的局部信息,使得算法既有全局搜索能力,又有局部区域精细搜索能力。当只对当前最优粒子进行局部搜索时,能较好地维持速度和精度的平衡。
(3)计算合力
模拟电磁理论的叠加原理,EMA通过计算合力来决定粒子的下一步走向。粒子i的电荷量qi决定了此粒子所受吸引力或排斥力的大小,电荷量qi的计算如式(13)所示,由此可知,目标函数值较优的粒子拥有较大的电荷数,具有更强的吸引力。作用在粒子i上的合力Fi的计算如式(14)所示。每两个粒子之间,目标函数值较优的粒子将吸引另一个粒子,目标函数值较劣的粒子会排斥另外一个粒子。由于当前最优粒子xbest的目标函数值最优,所以它是绝对吸引子,吸引所有其他粒子。
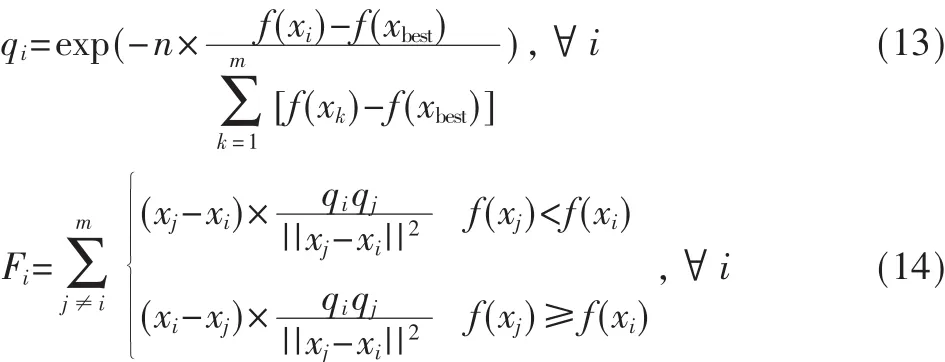
(4)移动系数[5]
计算移动步长是比较关键的一步,当步长较小时,对粒子的扰动较小,因而效果不明显。针对此情况,可以引入移动系数 k1和 k2,移动公式如式(15)所示,λ 在[0,1]上均匀分布,r表示第r维的分量,这样每个粒子都可以得到不同程度的更新,且扰动程度较大。k1和k2能明显地影响算法的收敛速度和解,根据经验,本文取k1=0.9,k2=1.0。

(5)终止准则
当达到最大迭代次数时,算法结束;否则,转到步骤(2)。
3 数值实验分析
某货物供应商有3个车场,且每个车场有不同类型的车辆,客户信息如表1所示,车场信息如表2所示。每辆车的最大配送里程为120 km。
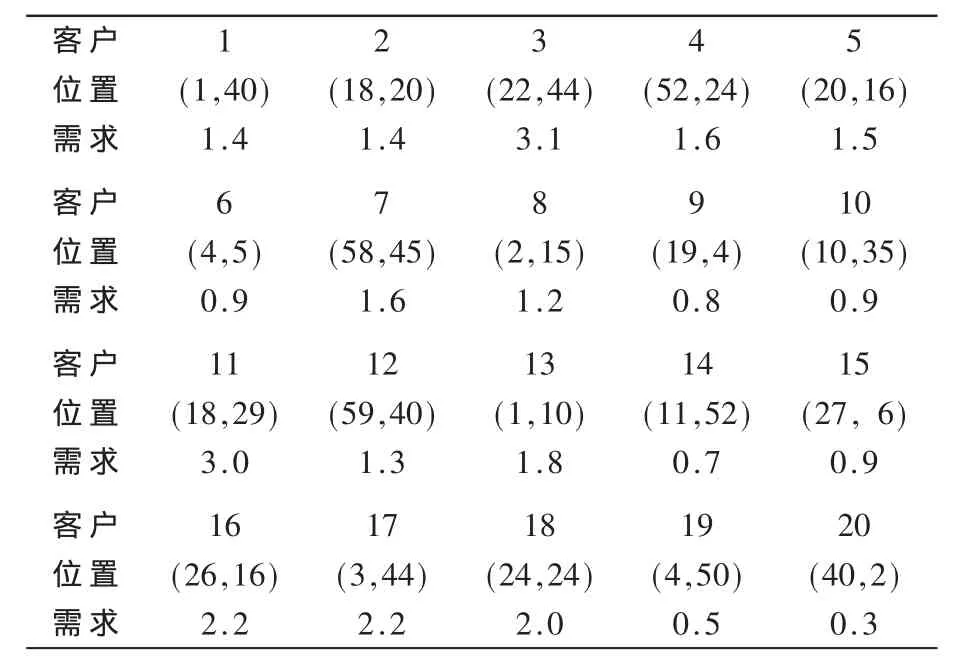
表1 客户信息表

表2 车场位置信息表
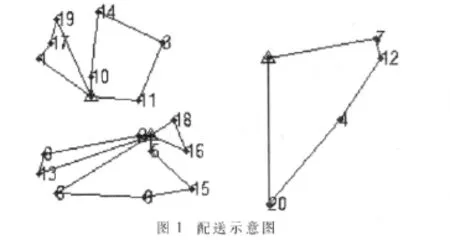
本文中的实验是在 Intel®CoreTMi3 CPU2.53 GHz、内存2.0 GB的PC机上采用Microsoft Visual C++6.0编程实现,关联系数由Microsoft Visual C++6.0随机产生。运行程序30次,某一代迭代例证如表3所示。得到该算法求解本算例的最优结果如表4所示,配送示意图如图1所示。
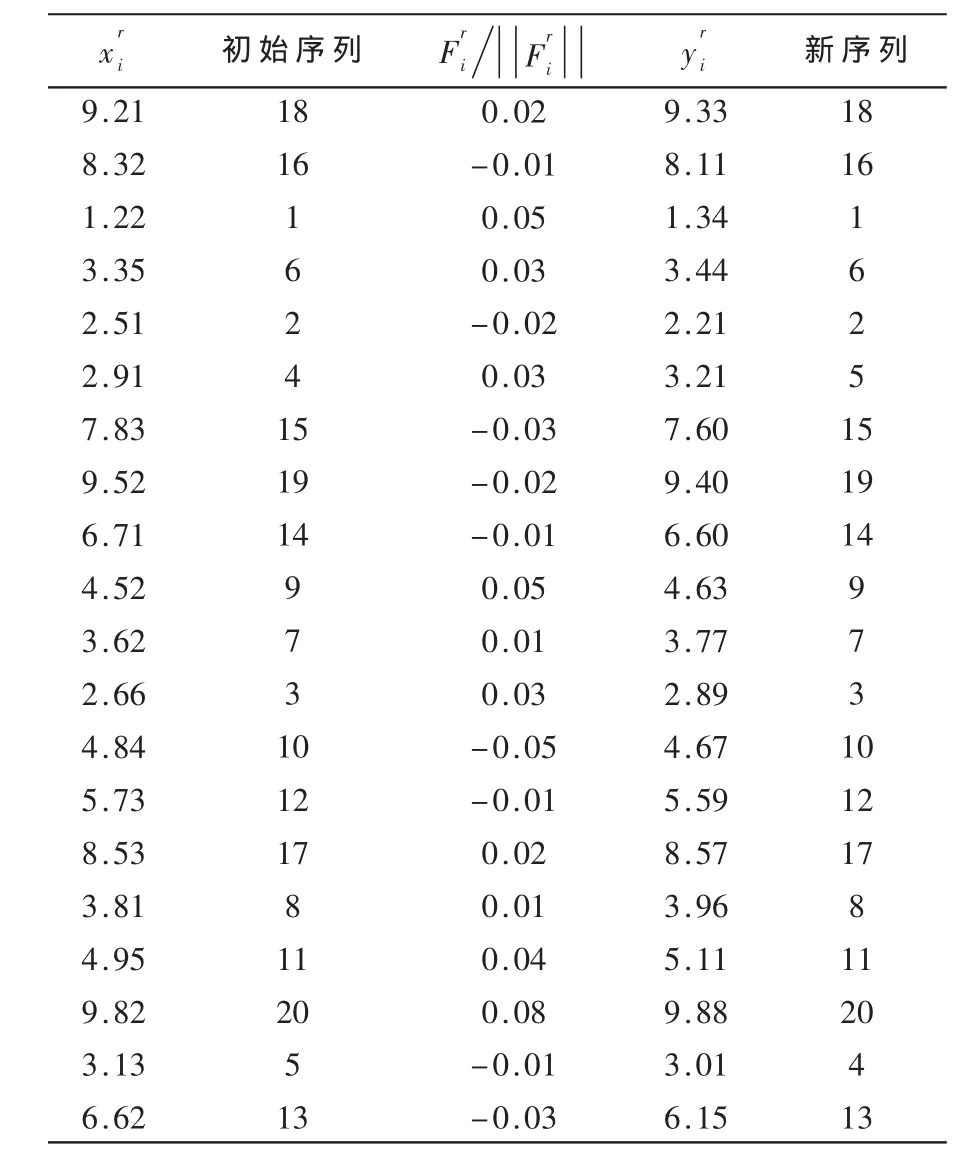
表3 迭代例证
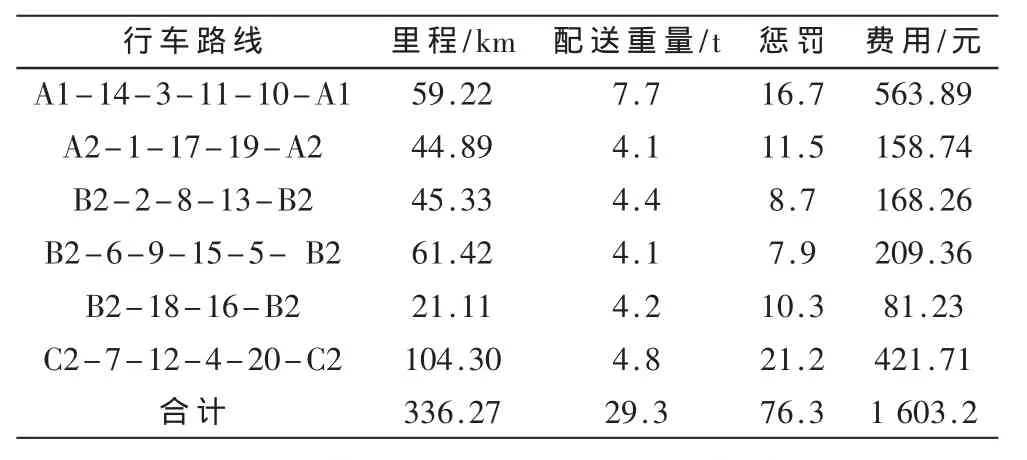
表4 最优配送方案
本文考虑关联运输调度问题的一种扩展特征——多车场多车型模型,并引入了移动系数,对传统的移动粒子步长进行改进,相当于对粒子添加扰动,使移动步长更为明显,从而增加了解空间的多样性。实验证明,改进的类电磁机制算法求解此类问题是有效可行的,而且具有更快的收敛速度,并得到了更优解。接下来可以将EMA运用到MDVRP、VRPTW、AVRP等模型中。
[1]韩丽霞,王宇平.求解无约束优化问题的类电磁机制算法[J].电子学报,2009,37(3):29-31.
[2]王晓娟,高亮,陈亚洲.类电磁机制算法及其应用[J].计算机应用研究,2006,23(6):67-70.
[3]韩丽霞,王宇平,兰绍江.基于模式搜索的类电磁算法求解约束优化问题[J].系统工程与电子技术,2009,31(9):2219-2222.
[4]尚云,何雪妮,雷虹.求全局最优的类电磁机制算法[J].计算机应用,2010,30(11):2914-2916.
[5]高亮,王晓娟,魏巍,等.一种改进的类电磁机制算法[J].华中科技大学学报(自然科学版),2006,34(11):4-6.

