饱和软黏土地基竖井施工扰动效应分析与评价*

黄雄立，韦 慧

(1.长沙理工大学交通运输工程学院，湖南 长沙 410004;2.湖南理大交通科技发展有限公司，湖南 长沙 410015)

针对软土地基上修建建筑物不能满足工程要求的稳定与变形问题，尽管目前有很多种地基处理方法，但排水固结法仍是实际工程中常用的有效方法。然而，在竖向排水体施工过程中，施工导管挤土作用会对地基土产生较大的扰动。砂井施工扰动很早就有学者认识到，并指出完全排土式砂井地基沉降稳定时间甚至要比不处理的地基要长［1］。工程实践结果同样表明:竖井打设使土体的结构发生扰动破坏，导致土体强度降低，地基承载力降低［2－4］;增加了建筑物的沉降［5－6］;影响竖井的排水效果。但上述更多的是集中在工程实录阶段，针对扰动机理的研究较少。因此，有必要对竖井施工扰动进行分析和评价。目前对竖井施工扰动效应的分析，广泛采用Vesic［7］圆柱形孔扩张弹塑性解理论，分析中大多将土体视为理想弹塑性材料，服从Tresca屈服准则或Mohr－Coulomb 屈服准则［8－10］。能够较好地反映软黏土应力应变关系的本构模型应为基于临界土力学概念的修正剑桥模型。Cao等在修正剑桥模型基础上给出了不排水扩张过程中土体应力的精确解析解，并分析了旁压试验、静力触探等土工原位测试问题［11－12］。但该精确解需要通过数值积分实现，实际应用不方便。本文根据文献［12］精确解的一种简化形式，对竖井施工过程中土体应力状态进行分析，并在此基础上评价了竖井施工扰动效应，建立了一个修正的扰动函数。

1 竖井周围土体应力变化

1.1 计算模型及基本方程

竖井的打设一般在短时间内就可完成，将此过程视为不排水条件下平面应变轴对称的圆柱形孔扩张问题，计算模型参见图1。假设饱和软黏土中圆孔的初始应力场、孔径为σ0和a0。当均匀分布的内压力从σ0增大到σa时，孔径从a0增大到a。随着内压力值的增加，围绕着圆孔的圆柱形区域将由弹性状态进入塑性状态，塑性区随σa的增加而不断扩大，rp为塑性区半径。分析井周应力状态时，弹性阶段本构方程为广义虎克定律;塑性区的屈服准则采用修正剑桥模型进行描述，表达式为:

图1 竖井的圆孔扩张分析模型Fig.1 Analytical model of cylindrical expansion for vertical drain

式中:q和p'分别为偏应力和有效平均应力;p'y为等向固结屈服应力;M为临界状态线的斜率。

由平面应变轴对称问题的平衡微分方程、几何方程和上述的屈服条件，圆柱形孔扩张问题塑性区的有关解答如下［12］。

有效应力q、p'与径向距离r的关系为:

偏应力比q与平均有效应力p'的关系:

式中:p'0为初始平均有效应力，p'0=σ0。

因此，联立式(2)和(3)，可得到q与r的之间关系，再根据应力平衡方程、边界条件和有效应力原理，可到孔压u与 r的关系［12］:

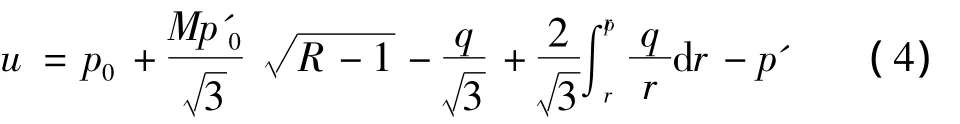
然而，式(4)的积分不能显式地表达，需通过数值积分计算，在实际应用不够方便。本文根据塑性区的偏应力与极限偏应力相差不大的事实［12］，假定塑性区的偏应力q等于极限偏应力qu，可得与上述相关的近似解答。

塑性区半径与孔径的关系为:

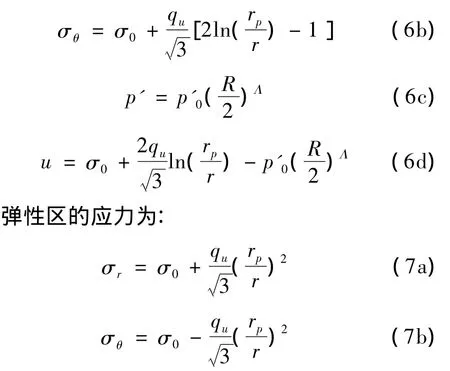
式中:σr和σθ分别为径向应力和环向应力。

1.2 孔周应力分布规律

修正剑桥模型相对于Tresca屈服准则和Mohr－Coulomb屈服准则可以考虑土体屈服应力(应力历史)的影响。根据等向平均有效应力p'和竖向有效应力σ'v的关系，可得到等向超固结比R与传统的竖向超固结比ROC的相互关系为［11］:

假设 G/p(0=30，M=1.2，Λ =0.75，取 ROC分别为1.0，1.5 和 3.0，根据公式(6)，(7)和(8)，分析了ROC对圆柱形孔周应力分布的影响。选取竖井施工对井周应力状态影响的特征量——超静孔压u和径向应力σr，其归一化的应力与径向距离的关系参见图2。由图可见:ROC越大，在孔周产生的u和σr越大，但衰减的速度越快，因此塑性区半径rp和影响范围越小;不同ROC的u和σr均随径向距离增加而呈对数衰减。

另外，对于天然沉积软黏土，ROC越大，表明屈服应力越大，土结构性越强，灵敏度就越大。因此，从另一方面表明灵敏度同样对孔周应力的分布有影响。关于灵敏度对挤土产生的超静孔压的影响，研究表明:沉桩过程中产生超静孔隙水压力与土的灵敏度有关，灵敏度越高的土中产生的孔压也越高［13］。

2 施工扰动效应评价

2.1 扰动评价及修正扰动函数的建立

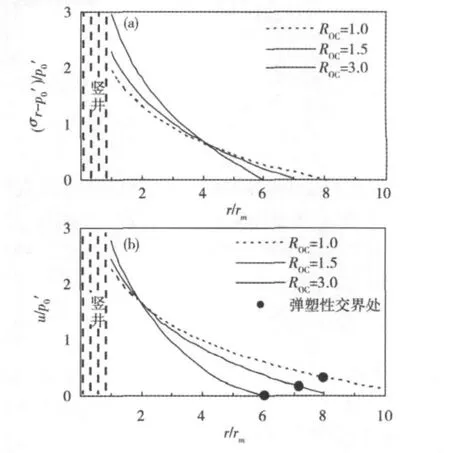
图2 超固结比(ROC)对圆柱形孔周应力分布的影响Fig.2 Effect of ROCon stress around the cylindrical cavity

竖井周围土体不排水强度因受到不同大小的施工扰动而不同程度的降低。文献［10］根据孔周应力在径向上呈对数衰减规律，假定扰动度在径向上亦为对数衰减。并认为在塑性区内，小孔壁即rm处扰动最大即完全扰动，此时饱和软黏土的不排水强度为重塑土的不排水强度;在弹塑性边界上，即rp处扰动度为0，不排水强度为原状土的强度Su;井周土体强度Sd与扰动度FD的关系为:

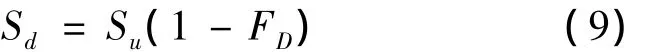
根据上式，结合灵敏度定义与上述假定，文献［10］提出一种基于饱和软黏土灵敏度St的扰动度函数，表达式为:

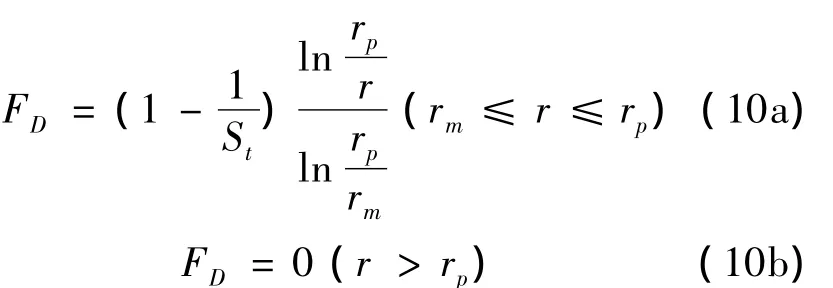
由前面的分析可知，扰动引起的超静孔压u在径向上为对数衰减，且受灵敏度的影响。因此，本文的扰动函数也采用基于灵敏度St的对数形式。但文献［10］定义的扰动函取值范围不是0～1，而是0～1－1/St，即在完全扰动的孔壁rm处扰动度不是其实际定义的100%，而是随灵敏度St变化而变化的，物理意义不够明确;另外，仅把塑性区当作竖井施工扰动区，只考虑塑性区的扰动，没有考虑弹性区的扰动，但实际中也有部分弹性区存在扰动［5，14，15］。鉴于此，对于灵敏性土，为了更加准确地描述竖井施工产生的附加扰动度，本文对文献［10］提出的扰动度函数进行修正，令其在扰动区的取值从1变化到0，表达式为:

式中:FD(Field disturbance)表示竖井施工造成的原位扰动;rp为塑性区半径，可由式(5)确定;rd为扰动区半径，根据此处扰动度FD=0的定义，得其表达式为:

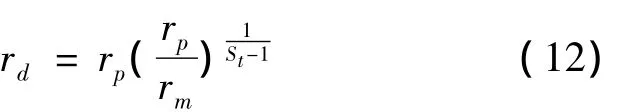
从式(12)可看出，扰动区半径rd随St的增大而减小:这与图2显示的规律是一致的。进而对扰动区的不排水强度重新定义:

根据扰动度FD是径向距离r对数函数的假定，修正的扰动函数进一步简化为:

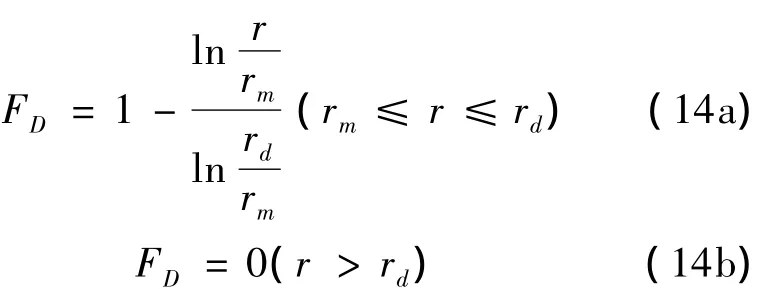
图3 施工扰动度FD随径向距离的变化Fig.3 Variation of FDwith radical distance

2.2 扰动函数的验证

竖井施工产生的附加扰动会降低井周土的水平向渗透系数。传统固结理论认为井周附近由于施工扰动存在一个涂抹区，并假定涂抹区内渗透系数是不变的，且涂抹区半径是2～4倍竖井等效半径。但最近有研究者根据室内试验和现场试验结果表明:施工扰动区不仅仅是涂抹区，且渗透系数在扰动区内不是不变的，而随扰动度的大小变化［16－18］。扰动区的渗透系数与扰动度FD的关系定义为:

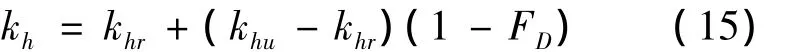
式中:kh为扰动区水平渗透系数;khr为完全重塑土水平渗透系数;khu为未扰动土水平渗透系数。

将式(14(a))代入式(15)，经化简后，得到归一化后的渗透系数与径向距离的关系为:

因此，根据式(16)计算的渗透系数结果，与本文收集到的一些文献中的试验结果进行比较，可以验证提出的扰动函数合理性。但相关文献中没有提供计算系数A和B所需的完整参数，本文只能对文献中的试验数据进行拟合，定性地检验扰动函数合理性。拟合结果见表1和图4。从表1和图4可以看出:不管是室内试验还是现场试验的结果，对数拟合系数均较高，与式 (16)所表示的趋势是一致的，表明本文所定义的扰动函数是合理、有效的。

图5所示为根据竖井(砂井和PVD)地基现场实测沉降反演得到的水平向固结系数Ch(e)经室内测得的原状样竖直向固结系数Cv归一化后，与井径比(dm为打设竖井套管按周长等效的直径)的关系。从图5可见:归一化的固结系数对数值与径向距离呈线性关系，即说明砂井地基固结系数随距井中心的径向距离增大而对数式增大。尽管图5所示为根据实测沉降反演的结果，分析的是竖井地基平均扰动度与径向距离的关系，但固结系数是随扰动度而变化的，且两者存在对数关系。因此，这也从另一方面说明了本文所给出的在径向上的对数扰动函数存在合理性。

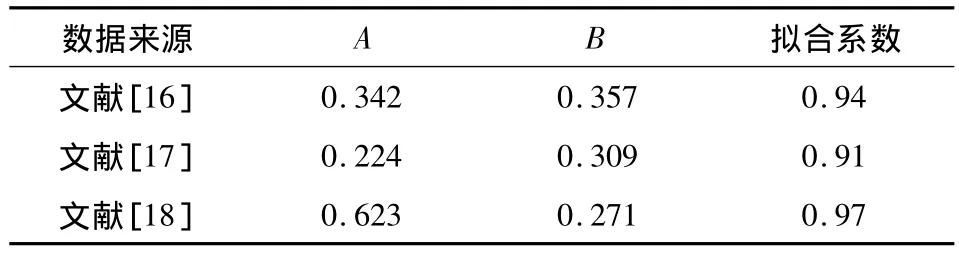
表1 试验数据拟合结果Table 1 Fitted results of test data

图4 归一化的渗透系数与径向距离的关系Fig.4 Relationship between normalized permeability coefficient and radical distance

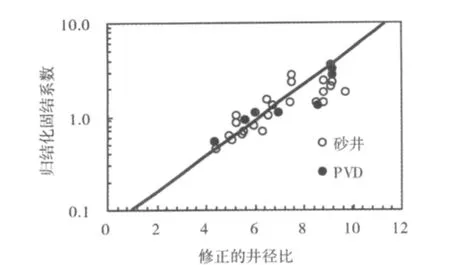
图5 归一化固结系数与修正的井径比关系［19］Fig.5 Relationship between Normalized consolidation coefficient and modified drain spacing ratio for vertical drains

3 结论

(1)采用修正剑桥模型作为屈服条件的圆柱孔扩张理论，得出竖井施工对井周应力状态影响的特征量即超静孔压u和径向应力σr在径向上呈对数衰减，且受地基土灵敏度的影响。

(2)在准确分析竖井地基扰动区范围和界定扰动函数取值范围的基础上，提出了修正的基于灵敏度考虑的对数扰动函数来评价竖井施工扰动影响。

(3)根据文献中竖井打设的室内模型试验与实际工程现场试验测得的固结指标随径向距离的变化结果，验证了所提出的扰动函数合理性，故式(16)为准确分析竖井地基的固结奠定了很好的基础。

［1］Casagrande L，Poulos S.On the effectiveness of sand drains［J］.Canadian Geotechnical Journal，1969，6(3):286－326.

［2］Akagi T.Effect of mandrel driven sand drains on strength［C］//Proceeding of the Tenth International Conference on Soil Mechanics and Foundation Engineering.1981.

［3］施建勇，赵维炳，艾英钵，等.砂井施工对软黏土扰动的研究［J］.河海大学学报，1997 ，25(2):30－33.SHI Jian-yong，ZHAO Wei-bing， AI Ying-bo，et al.Effect of sand drainage construction on soft clay disturbance［J］.Journal of Hohai University:Natural Sciences，1997，25(2):30 －33.

［4］邹新军，杨 眉，赵明华.基于室内模型试验的砂井复合地基作用机理［J］.铁道科学与工程学报，2009，6(3):61－64.ZOU Xin-jun，YANG Mei，ZHAO Ming-hua.Behavior of the sand well composite foundation by indoormodel test［J］.Journal of Railway Science and Engineering，2009，6(3):61－64.

［5］刘吉福，杨春林.珠江三角洲地区竖向排水体施工扰动初探［J］.岩石力学与工程学报，2003，22(1):142－147.LIU Ji-fu，YANG Chun-lin.Preliminary study onconstruction disturbance of vertical drainage bodies in the pearl river delta［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22(1):142 －147.

［6］王立忠，李玲玲.结构性土体的施工扰动及其对沉降的影响［J］.岩土工程学报，2007，29(5):697 －704.WANG Li-zhong，LI Ling-ling.Field disturbance of structured clay and its effect on settlements of soil foundation［J］.Chinese Journal of Geotechnical Engineering，2007，29(5):697 －704.

［7］Vesic A S.Expansion of cavities in an infinite soil mass［J］.Journal of Soil Mechanics and Foundation ，ASCE，1972 ，98(3):265－291.

［8］徐永福，傅德明.结构性软土中打桩引起的超孔隙水压力［J］.岩土力学，2000，21(1):53－55.XU Yong-fu，FU De-ming.Excess pore pressure induced in piling in saturated structural soft soils［J］.Rock and Soil Mechanics，2000，21(1):53 －55.

［9］张仪萍，王 伟.竖井施工对软土地基的扰动效应研究［J］.浙江大学学报:工学版，2006，40(7):1239－1243.ZHANG Yi-ping， WANG Wei. Study on disturbance effect on soft soil ground during vertical drain construction［J］.Journal of Zhejiang University:Engineering Science，2006，40(7):1239 －1243.

［10］徐书平，刘祖德，司马军.考虑扰动的饱和软黏土球形孔扩张弹塑性解［J］.岩石力学与工程学报，2006，25(1):3212－3217.XU Shu-ping，LIU Zu-de，SI Ma-jun.Elato－plastic solution of spherical cavity expansion considering disturbed saturated soft clay［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(1):3212 －3217.

［11］Cao L F，Chang M F，Teh C I.Cavity expansion in modified Cam Clay and its application to the interpretation of piezocone tests［R］.Singapore:Geotechnical Research ReportNTU/GT96－03，Nanyang Technological University，1996.

［12］Cao L F，Teh C I，Chang M F.Undrained cavity expan-sion in modified cam clay.I:Theoretical analysis［J］.Geotechnique，2001，51(4):323 －334.

［13］Poulos H G，Davis E H.Pile foundation analysis and design［M］.London:John Wiley and Sons，1980.

［14］王 军，高玉峰，高红珍.结构性软土地基施工扰动定量分析［J］.岩土力学，2005，26(5):789－794.WANG Jun，GAO Yu-feng，GAO Hong-zhen.Quantitative analysis of foundation treatment disturbance of structured soft clay ground［J］.Rock and Soil Mechanics，2005，26(5):789 －794.

［15］雷金山，杨秀竹，夏力农，等.软土地层花管压密注浆的有限元模拟［J］.铁道科学与工程学报，2009，6(3):28－30.LEI Jin-shan，YANG Xiu-zhu，XIA Li-nong，et al.Finite element smiulation on compaction grouting with bored pipe in soft soil［J］.Journal of Railway Science and Engineering，2009，6(3):28 －30.

［16］Onoue A，Ting N H，Germaine J T，et al.Permeability of disturbed zone around vertical drains［C］//Proceedings of the Congress of the Geotechnical Engineering Division，American Society of Civil Engineers.New York，1991:879－890.

［17］Madhav M R，Park Y M，Miura N.Modeling and study of smear zones around band shaped drains［J］.Soils and Foundations，1993，33(4):135 －147.

［18］Sathananthan I，Indraratna B.Laboratory evaluation of smear zone and correlation between permeability and moisture content［J］.Journal of Geotechnical and Geoenvironmental Engineering，2006，132(7):942 －945.

［19］Saye S R.Assessment of soil disturbance by the installation of displacement sand drains and prefabricated vertical drains［J］.Geotechnical Special Publication，2003:372－393.