横向地震激励下的悬索桥车－桥耦合动力响应分析*

彭荣华，王 柳，郭向荣

(中南大学土木工程学院，湖南 长沙 410075)

随着我国大跨径桥梁的大规模建设，桥梁的动力特性和车桥耦合动力响应问题往往是设计中的主要控制因素之一。悬索桥是特大跨度桥梁的主要桥式之一。悬索桥在公路桥梁中应用较多，但在铁路桥梁或公铁2种桥梁中应用相对较少。由于特大跨度悬索桥刚度较小，当列车活载通过时，悬索桥主缆几何形状会发生改变，从而引起桥跨结构产生较大的竖向挠曲变形;在列车动荷载作用下车桥耦合系统容易产生较大幅度的振动响应，影响桥梁和轨道结构的可靠性和列车的运行安全性及平稳性［1］。而主缆和吊索初始内力对悬索桥的整体刚度影响较大，因此，进行地震—车—桥耦合振动分析时，也应该考虑主缆初始内力对车桥耦合振动的影响［2］。地震是一种具有很大破坏力的自然现象。地震发生时，桥梁由于受到地震荷载的激扰而产生强烈的振动，影响桥梁结构以及桥上列车的运营安全。我国铁路设计标准的不断提高，为保证线路的平顺度和稳定性，桥梁在线路中所占的比例越来越大，这样地震发生时列车在桥上的概率就相应地变大［3］。本文根据弹性系统动力学总势能不变值原理［4］及形成矩阵的“对号入座”法则［5］，将轨道不平顺作为系统的自激激励源，地震作为外部激励［6］，建立考虑地震作用的车桥系统耦合振动方程及分析模型。以重庆市江津区几江悬索桥为例，采用计算机模拟的方法，建立悬索桥的车桥耦合动力分析的有限元分析模型，对横向地震激励下桥上列车的走行性进行研究，分析横向地震对车桥系统耦合动力响应的影响。

1 地震作用下车—桥系统力学分析模型

地震荷载作用下车一桥空间耦合振动分析模型是由车辆子系统、轨桥子系统按照一定的轮轨关系联系起来的空间耦合大系统，将地震荷载作为外部激励作用于该系统上［7－8］。

车辆子系统是由若干节车辆组合而成的列车，每节车辆又是由车体、转向架、轮对以及弹簧一阻尼悬挂装置组成的复杂的多自由度振动系统。车辆空间振动分析模型采用以下假定:(1)车体、转向架和轮对均假设为刚体;(2)不考虑机车、车辆纵向振动及其对桥梁振动与行车速度的影响;(3)轮对、转向架和车体均作微振动;(4)所有弹簧均为线性，所有阻尼按粘滞阻尼计算，蠕滑力按线性计算;(5)沿铅垂方向，轮对与钢轨密贴，即轮对与钢轨的竖向位移相同。基于上述假定，车体空间振动有:侧摆、侧滚、摇头、点头、浮沉等5个自由度;每个构架有侧摆、侧滚、摇头、点头、浮沉5个自由度;每个轮对有侧摆，摇头等2个自由度，故每辆四轴车辆共有23个自由度，每辆六轴机车共有27个自由度［4］。

根据弹性势能不变值原理及“对号入座”法则，可以得到任意时刻，车桥系统的空间振动方程。

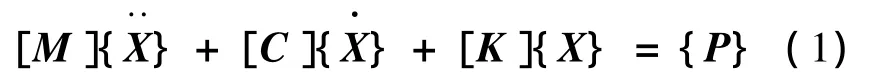
通过式(1)还不能求得车桥系统的振动响应，因为式(1)的荷载列阵仅含列车重力，直接求解方程得到的只是列车重力下的静力响应。因此，需要增加列车的蛇形波和轨道不平顺函数来替换式(1)中的振动参数。

在横向地震荷载作用下，桥梁将与地面一起运动，此时将桥梁结构的自由度分为有地震输入的支承点自由度和无地震输入的非支承点自由度。整个桥梁体系的运动方程按结构非支承点和地面支承点分块，则在各支承处受到不同的地震激励作用时，桥梁结构的运动方程可写为［3，9－10］:

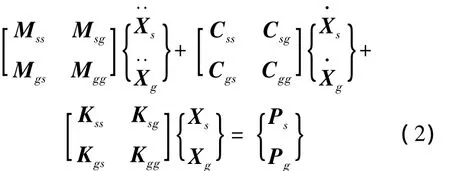
其中:Pg为基础作用于结构上的力;Ps为非支承处的外荷载向量和Xs分别为非支承处自由度的加速度、速度和位移向量;Mss，Css和Kss分别为非支承处自由度质量、阻尼和刚度矩阵;和Xg分别为支承处自由度的加速度、速度和位移向量;Mgg，Cgg和Kgg分别为支承处自由度质量、阻尼和刚度矩阵;Msg，Csg和Ksg分别为桥梁结构地面支承节点对非支承节点的质量、阻尼和刚度矩阵;Mgs，Cgs和Kgs分别为非支承节点对桥梁结构地面支承节点的质量、阻尼和刚度矩阵;这2组矩阵反映了结构非支承节点自由度与支承节点自由度间的相互影响。

地震发生时，结构支承点自由度满足的边界条件为:

在地震作用下结构分析中，地震波的输入方法主要有直接求解法、拟静力位移法和大质量法。本文采用的计算方法是直接求解法，将式(2)展开可得:

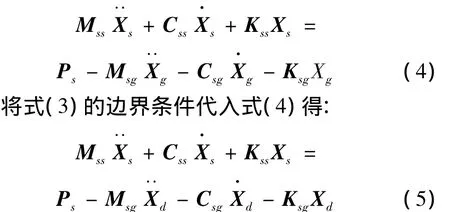
本文应用Wilson－θ逐步积分法直接求解地震荷载作用下车一桥耦合系统振动方程。

2 工程背景及计算模型

以重庆市江津区几江悬索桥为研究对象。几江大桥跨径布置为(50+600+65)m，为公铁两用悬索桥，其全桥示意图见图1。主梁为双幅单层桥面方案，两侧的钢箱梁通过中间的桁架连接。连接桁架段宽10 m，桁高4.2 m，两侧的钢箱梁宽为13.5 m。线路布置为双向六车道+双线轨道交通，轨道交通线布置在桁架段上，轨道线间距4.1 m，汽车车道布置在两侧的钢箱梁上，两侧人行道各宽2 m，整个桥面全宽41 m。其示意图见图2。主塔塔身采用钢筋混凝土门式框架，塔柱为梯形钢筋混凝土截面，上、下两道横梁为预应力空心箱型截面。主缆矢高为66 m，吊索间距为12 m。

由此可见，MRI检查的骨髓成像能力和软组织分辨率较强，相较于X线和CT影像学检查来说其有一定的优势性。MRI能够实现多方位成像[3]，将关节病变明显的显示出来，是当前用于PVNS诊断较为理想的方法，具有较高的应用价值。

图1 几江悬索桥示意图Fig.1 Configuration of the Jijiang suspension bridge

图2 主梁横断面图Fig.2 Cross section of the main beam

几江悬索桥采用有限元方法建立桥梁动力分析模型。以主跨跨中断面的桁架横梁中点作为几何模型的原点，以桥梁横向为坐标系X轴方向，桥梁竖向向下为Y轴方向，顺桥向为Z轴方向。本文对于该桥不同类型的结构部位，本文采用了相应的不同单元来模拟。主缆、吊索单元均采用空间杆单元，主缆考虑了恒载产生的初始索力对其结构初始刚度的影响;主梁的两幅钢箱梁采用板单元建模，两幅钢箱梁之间的横向联系梁采用空间梁单元建模;桥墩、桥塔以及桩基均采用空间梁单元来模拟;主缆和桥塔顶、墩粱和塔梁间采用主从约束处理;主缆两端固结于地面上，桩基结构采用m值法考虑桩土的共同作用;二期恒载按线荷载分别作用于2条行车线上。桥梁系统的阻尼按Rayleigh阻尼考虑，弹性模量E和泊松比μ按现行桥规取值。图3所示为其三维有限元分析模型。

图3 悬索桥有限元分析模型Fig.3 Finite element model of the suspension bridge

根据前述分析模型与计算原理，对几江大桥悬索桥进行地震作用下列车—桥梁耦合系统空间振动响应计算。本文的计算地震波采用50年超越概率为10%的人工地震波。修正后的地震加速度时程曲线如图4所示。其横向加速度峰值为63 Gal，本文计算中不考虑地震波的行波效应和多点激励的影响。

图4 横向地震波加速度时程曲线图Fig.4 Curve of lateral seismic acceleration

计算中列车采用B型车，其6辆列车编组为:1辆动车+1辆拖车+2辆动车+1辆拖车+1辆动车，列车运行速度分别取 80，90，100，110，120，130和140 km/h，轨道不平顺数值按照美国六级谱生成的轨道不平顺样本值取用。计算步长取0.005 s，共计算20000步，计算总时长为100 s。结构阻尼比为1%。为了对比分析，本文也计算了该桥无地震作用下的车桥动力响应。

3 地震荷载作用下车桥系统耦合振动的动力响应

图5～8所示分别为在横向地震和无地震荷载作用的情况下，列车以140 km/h的速度通过几江悬索桥时，主跨跨中的横竖向响应时程曲线的比较。在图5～8中，实线均表示无地震作用，虚线均表示横向地震作用。

从图5～8可以看出:有地震作用下悬索桥的横向动力响应时程完全不同于无地震作用;当没有地震荷载作用在车—桥耦合系统上时，桥梁跨中的横向位移响应很小，接近于0 cm;当有横向地震荷载激励时，桥梁跨中的横向位移和横向加速度的最大值均较无地震时有大幅度增加。这是因为无地震作用时桥梁结构在横向只受到轨道不平顺的影响，而在地震发生时却同时受到很强的横向地震波激扰。有震和无震情况桥梁下结构的竖向位移时程曲线完全重合，竖向加速度响应略有变化，这是因为本文在计算中未考虑竖向地震荷载作用。

图5 桥梁主跨跨中横向位移时程曲线Fig.5 Lateral displacement curve of bridge at middle main－span

图6 桥梁主跨跨中横向加速度时程曲线Fig.6 Lateral acceleration curve of bridge at middle main－span

图7 桥梁主跨跨中竖向位移时程曲线Fig.7 Vertical displacement curve of bridge at middle main－span

图8 桥梁主跨跨中竖向加速度时程曲线Fig.8 Vertical acceleration curve of bridge at middle main－span

图9所示为有、无地震荷载作用的情况下，列车的横竖向振动加速度和横竖向Sperling舒适性指标随着列车行车速度提高的变化趋势。

表1和表2所示分别列出了有、无地震荷载激励下，在单双线行车条件下，列车分别以80～140 km/h的速度通过桥梁时，桥梁主跨跨中最大动力响应值和桥上列车最大动力响应值。

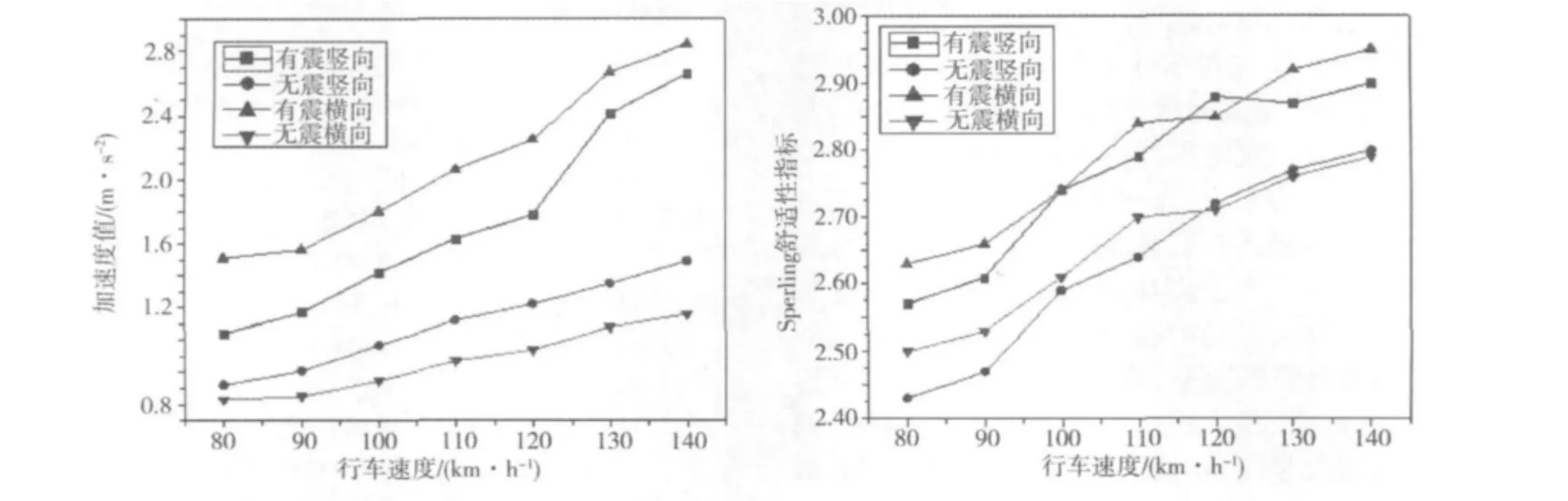
图9 不同行车速度下列车振动加速度(左)和Sperling舒适性指标(右)Fig.9 Vehicle vibration acceleration(left)and Sperling comfort index(right)under different vehicle speed

表1 桥梁主跨跨中最大动力响应值Table 1 Maximum dynamic response of bridge at middle main－span

表2 桥上列车最大动力响应值Table 2 Maximum dynamic response of vehicles

从表1可以看出:在横向地震荷载作用下，桥梁跨中的横向位移和横向加速度的最大值均比无震时大很多，而竖向位移和竖向加速度的最大值几乎没有变化，这表明了横向地震作用对桥梁的竖向动力响应影响很小。悬索桥主跨跨中最大竖向位移为47.6 cm，最大横向位移为17.84 cm，桥梁的动力响应位移最大值均在容许值以内。在不同的行车速度的双线与单线行车情况下，桥梁跨中的横向位移和加速度的最大值比较接近，这说明横向地震荷载对桥梁的横向动力响应起控制作用。

从表2和图9可以看出:横向地震荷载作用下列车的轮轨间的横向力、轮重减载率以及脱轨系数等的最大值都比没有地震荷载激励时的大，这表明横向地震荷载导致列车行车安全性下降。在所有的计算工况中，地震荷载作用下的各项列车响应指标均小于相应的规定限值。在有震和无震情况下，列车的振动加速度和Sperling舒适性指标都随列车运行速度的提高有明显的增大趋势，并且有地震作用时的增幅要大于对应的无震情况。横向地震激励对列车横向振动的影响大于其对竖向振动的影响。所有计算工况中，列车车体的最大竖向加速度为 2.66 m/s2，最大横向加速度为 2.84 m/s2;列车运行的最大竖向Sperling舒适性指标为2.90，最大横向Sperling舒适性指标为2.95;舒适度指标小于相应的规定限值。至于在强烈地震激励下的车—桥耦合系统的动力响应有待于进一步计算和分析。

4 结论

(1)在计算横向地震荷载作用下，当单线或双线B型车分别以80～140 km/h通过几江悬索桥时，列车行车安全性满足相关规范的要求。

(2)横向地震荷载对悬索桥的横向动力响应具有显著的影响，对悬索桥的竖向动力响应影响不大;因此在计算悬索桥的车—桥耦合系统动力分析时的桥梁横向动力位移，应考虑横向地震荷载的作用。

(3)横向地震激励下悬索桥上列车的脱轨系数、轮重减载率、轮轨间横向力、车体横竖向加速度以及Sperling舒适性指标有大幅度增加，因此，在评判悬索桥上的列车运行的安全性与舒适性须考虑横向地震荷载的影响。

(4)桥上列车运行速度对横向地震荷载作用下悬索桥的动力响应影响不大，但对于列车运行的安全性与舒适性有很大影响，因此，在仅需计算地震激励下悬索桥结构本身的动力响应时，可以不考虑行车速度变化对桥梁响应的影响。

［1］李小珍，刘德军，晋智斌.大跨度铁路悬索桥车线桥耦合振动分析［J］.钢结构，2010，12(25):6－12.LI Xiao-zhen，LIU De-jun，JIN Zhi-bin.Analysis of train －track－bridge coupled vibration of a railway long－span suspension bridge［J］.Steel Construction，2010，12(25):6－12.

［2］朱仲毅.独塔自锚式悬索桥恒载状态下结构线形及内力分析［J］.铁道科学与工程学报，2005，2(2):46－50.ZHU Zhong-yi.Analysis of the geometry and inner force for self－anchored suspension bridge with single－tower under dead load［J］.Journal of Railway Science and Engineering，2005，2(2):46 －50.

［3］翟婉明，夏 禾.列车—轨道—桥梁动力相互作用理论与工程应用［M］.北京:科学出版社，2011.ZHAI Wan-ming，XIA He.Train － track － bridge dynamic interaction:Theory and engineering application［M］.Beijing:Science Press，2011.

［4］曾庆元，郭向荣.列车桥梁时变系统振动分析理论与应用［M］.北京:中国铁道出版社，1999.ZENG Qing-yuan，GUO Xiang-rong.Theory and application of train－bridge tmie－variant system vibration analysis［M］.Beijing:China Railway Press，1999.

［5］曾庆元，杨 平.形成矩阵的“对号入座”法则与桁段有限元法［J］.铁道学报，1986，8(2):48 －59.ZENG Qing-yuan，YANG Ping.The“set－ in － right－ position”rule for formulating matrix and the truss finite element method for spatia l truss analysis［J］.Journal of the Raiwlay Society，1986，8(2):48 －59.

［6］邓子铭，郭向荣，张志勇.地震作用对钢桁梁桥车桥系统耦合振动的影响分析［J］.中南大学学报:自然科学版，2011，42(1):184 －191.DENG Zi-ming，GUO Xiang-rong，ZHANG Zhi-yong.Coupled virbration of train－bridge system of steel truss bridge with seismic effect［J］.Journal of Central South University:Science and Technology，2011，42(1):184 －191.

［7］韩 艳，夏 禾，郭微微.斜拉桥在地震与列车荷载同时作用下的动力响应分析［J］.工程力学，2006，23(1):93－98.HAN Yan，XIA He，GUO Wei-wei.Dynamic response of cable－stayed bridge to running trains and earthquakes［J］.Engineering Mechanics，2006，23(1):93 － 98.

［8］夏 禾.车桥与结构动力相互作用［M］.北京:科学出版社，2002.XIA He.Dynamic interaction between vehicles and structures［M］.Beijing:Science Press，2002.

［9］韩 艳.地震作用下高速铁路桥梁的动力响应及行车安全性研究［D］.北京:北京交通大学土木建筑工程学院，2005.HAN Yan.Dynamic response of high － speed railway bridges and running safety of vehicles during earthquakes［D］.Beijing:School of Civil Engineering Beijing Jiaotong University，2005.

［10］郑史雄，奚绍中.大跨度钢构桥的地震反应分析［J］.西南交通大学学报，1997，32(6):586 －591.ZHENG Shi-xiong，XI Shao-zhong.Seismic response analysis of long span rigid frame bridges［J］.Journal of Southwest Jiaotong University，1997，32(6):586 －591.