有限回程开销多小区分布式协作波束成形技术

黄永明，杜颖钢，余辉，杨绿溪

（1. 东南大学 教育部水声信号处理重点实验室，江苏 南京 210096;2. 东南大学 信息科学与工程学院，江苏 南京210096; 3. 华为技术有限公司 通信技术研究部，广东 深圳 518129）

1 引言

蜂窝网络中频率复用的多小区多用户系统是一个干扰受限系统。小区边缘用户由于距基站较远而离干扰小区较近，其链路可靠性较差，传统的抗干扰技术已无法满足日益提高的系统平均频谱利用率要求，而多小区协作处理是解决该问题的有效策略之一。它通过相邻基站的协作能有效抑制小区间干扰，甚至能将干扰转变为增益。理论研究已表明：相比非协作多小区系统，该策略可显著提升链路可靠性和系统容量。该方向早期研究主要针对上行链路多个基站联合接收用户信号的优化设计。相比而言, 多小区下行链路的协作处理优化更具挑战性，尤其当基站配置多根天线并考虑单基站功率约束条件。

通过多个协作基站之间信道状态信息(CSI,channel state information)和用户数据信息的完全共享，多基站协作模型本质上可等效为单小区的多用户多天线系统。现有的下行链路多用户技术可直接应用于该模型并理论上获得吞吐量的明显提升。但其实现需要一个中央控制器且需要多小区用户之间进行精确地同步，这在实际系统中很难达到；此外，基站间进行大量的信息交互，所需的回程开销现有系统难以承受。因此迫切需要发展基于小区间有限协作的分布式多小区协作处理技术。

分布式多小区协作传输技术近几年已得到了广泛的关注，文献[1]和文献[2]研究了多小区下行链路分布式处理技术的可达速率性能，文献[3]进一步分析了有限回程约束下的容量性能，揭示了该技术的潜在增益。文献[4～6]给出了多小区分布式协作处理的具体算法。其中，文献[5]在基站间共享数据信息的情况下，将下行链路的波束成形问题转化为线性最小均方误差(LMMSE)估计问题，实现了分布式波束成形的迭代优化，但该算法不能保证全局收敛性。文献[6]仅利用本地的信道状态信息实现分布式的多小区协作波束成形设计，可获得接近于帕累托界（Pareto boundary）的准最优性能。但需指出的是，文献[5]和文献[6]均需要基站间共享数据信息，这在有限回程容量限制下很难实现。

为了有效降低协作基站之间的信息交互，文献[7～10]提出了基站间不共享数据信息的协作波束成形算法。文献[7]利用 Lagrange对偶理论实现了基于小区间有限信息交互的协作波束成形优化，但它只能解决给定 SINR要求下的最小化总功率问题；文献[8]和文献[9]在仅利用本地信道状态信息的条件下，分别基于 SGINR（signal-to-generatedinterference plus noise ratio）和 SCIR（signal-tocaused-interference ratio）准则提出了协作预编码的分布式优化算法。但该算法只在两基站协作场景下高系统信噪比时具有渐进最优性。

本文将研究有限回程开销约束下的多小区协作波束成形优化设计。为了实现用户公平性基础上的系统性能优化，提出以逼近多用户速率集合帕累托界上具有最大最差用户速率的点为优化目标。基于该目标，首先推导出一种能达到目标点的集中式算法，算法分为最小信干噪比（SINR）最大化（max-min）优化和帕累托改进 2个步骤。在此基础上，进一步提出了一种逼近集中式算法性能的分布式解决算法，该算法利用多小区系统的上下行链路对偶性原理，将下行链路优化问题转化为虚拟的上行链路优化问题，从而实现了小区间有限协作约束下的分布式协作波束成形优化设计。

2 系统模型

考虑一个频率复用因子为1的协作多小区下行链路系统，包含K个基站和U个用户，每个基站配置M根发射天线，每个用户终端配置单根天线且从属于单个基站。各基站只向从属于自己的用户发送信号，因此基站之间不需要共享用户数据，但各用户的发送波束需进行协作优化设计，以有效抑制小区间干扰并提升系统性能。

为方便分析，先假定每个基站仅服务单个用户，即K=U。令基站k发往其所服务用户（同样标记为k）的信号记为ks，满足其中，E ｛·｝为期望运算符。令和kp 分别表示基站k的归一化波束成形向量和发射功率，则用户k的基带等效接收信号可表示为

其中，†表示Hermitian转置，向量kih为基站i到用户k的平坦衰落信道为高斯白噪声。

需要指出的是，由于本文算法的优化目标为信干噪比的简单函数，上述接收信号模型不需要各基站发射信号在接收端的严格同步。这是因为实际系统中可能产生的信号不同步在 OFDM 系统中可等效为信道矢量的相位偏移，并不影响接收端的SINR值。

上述协作多小区系统设计的关键在于功率分配｛pk｝∀k和波束成形向量｛fk｝∀k的联合优化，可分为集中式优化和分布式优化2种方式。实际系统中多小区之间的回程链路容量有限，因此协作波束成形优化设计还需充分考虑回程开销的约束。

3 集中式协作波束成形技术

本节将提出一种集中式协作波束成形方法。为了实现公平性基础上的性能优化，所提方法首先采用最大化最差用户(max-min)加权SINR准则优化设计多小区下行波束成形向量和功率分配向量，然后提出一种帕累托改进方法，以在不牺牲其他用户性能的基础上最大限度地提升单个用户的 SINR性能。由于用户速率和SINR单调相关，所提方法可逼近帕累托界上具有最大最差用户速率的点。下面将详细讨论这种2步优化算法。

3.1 Max-min优化

各用户的SINR 计算如下

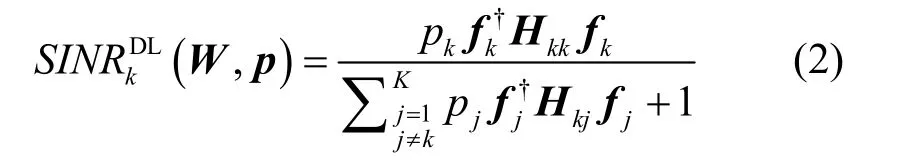
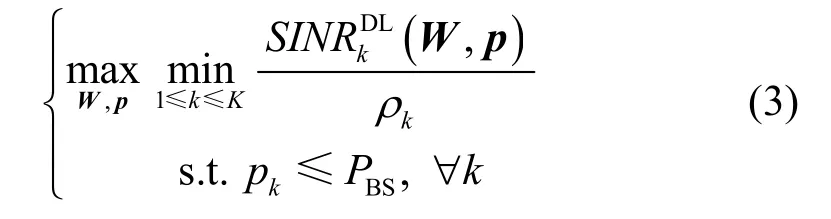
式(3)中BSP为各基站的功率约束，kρ为权重因子，通过为各个小区设定不同的权重因子可以实现比例公平的优化，设置较大权重因子的用户可获得较高的速率。上述问题是非凸的，很难直接求解。下面把原始问题等效成2个子问题进行分层求解。引入虚拟加权SINR指标γ，并定义如式(4)的功率最小化子问题（内层子问题）：

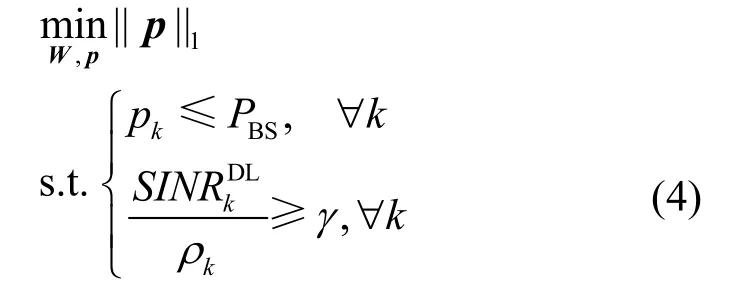
其中，||p||1表示向量p的一范数。对于不同γ，该问题分为有解和无解2种情况。研究已表明[11]，该子问题能转换为二阶锥规划问题，因此可用 CVX之类的凸优化工具包进行求解。当给定γ有解时，对应的功率向量解记为γ(p)。作者在文献[12]中的研究已指出，问题(3)的求解等效于寻找使对应问题(4)有解的最大虚拟加权SINR指标γ*，该子问题（外层子问题）可表示为

获得该最大指标的对应波束成形向量W*和功率向量p*即为问题(3)的解。

基于上述结论，类似文献[12]中的分层迭代算法，利用二分搜索法迭代优化虚拟加权SINR指标并输入到子问题(4)进行求解，直至所得功率分配向量中至少有一个元素等于功率约束PBS,对应的波束成形向量集和功率分配向量即为问题(3)的解。

3.2 帕累托改进（Pareto improvement）

上述的max-min优化虽然可以有效地最大化簇内最差小区的速率性能，但每个用户总是得到完全相等的加权 SINR，且下行功率向量*p大部分元素往往都小于PBS（对应的用户集合记为S），表明在max-min优化性能的基础上，系统和速率仍有一定的提升空间。为此，本文提出一种波束成形向量的更新方法，在max-min优化结果的基础上进一步调整用户k∈S的波束成形向量和发射功率，使得这些用户在不降低其他任一用户 SINR（或速率）的前提下进一步提高自身的SINR（或速率），博弈论中这种方法称为帕累托改进。具体算法描述如下：

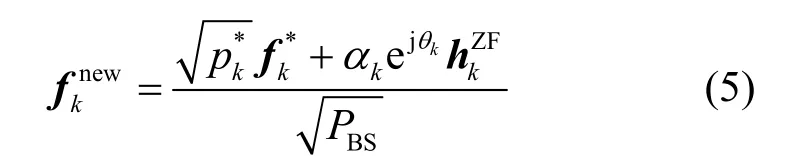
其中，kα为标量因子，使得

3.3 性能分析

下面将证明上述帕累托改进方法在不损害其他用户性能的前提下通常可最大限度地提高自身的性能。博弈理论把最大限度帕累托改进后获得的多用户速率域称为帕累托界，文献[2]已证明帕累托界上各用户的波束成形向量必能表示为如下形式：

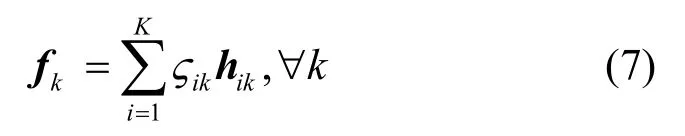
其中，ikς表示复数参数。类似的方法可证明，maxmin最优的用户波束成形矢量同样可表示成上述形式。进一步改写式（7）为

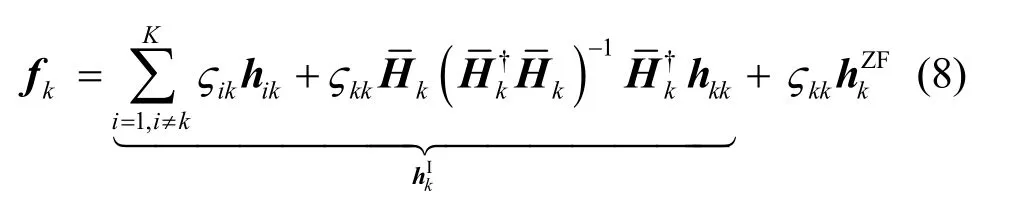
把kf分解成ZFkh 和Ikh2个方向。由于通常有为了保证用户波束成形更新后不损害其他用户的性能，需把帕累托改进波束更新方向限制在 hkZF方向，表示如下：

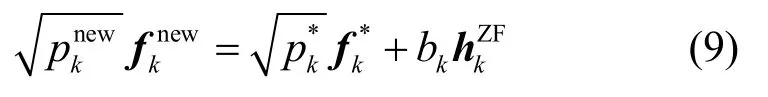
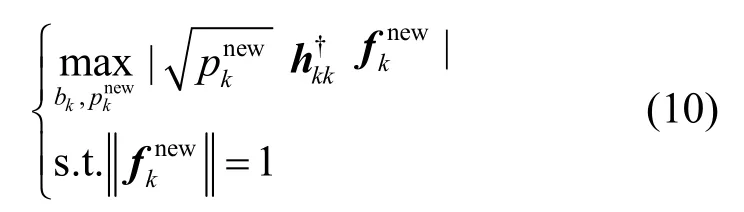
4 分布式协作波束成形技术

基于上节提出的集中式优化方法，本节将进一步提出低回程开销的分布式优化方法，所提方法同样分成2个步骤，即max-min优化步骤以及帕累托改进步骤。本文主要考虑TDD系统，利用上下行信道的互易性，假设基站端通过信道估计可获得各用户的下行链路信道信息[12]，记为基于该本地信道信息，由式(5)可知，每个协作基站可分布式地实施帕累托改进，基站之间不需要交互任何信息。因此，分布式优化的关键在于max-min优化步骤的分布式实现。下面本文利用多小区协作系统中上下行链路的近似对偶性原理提出一种max-min优化的分布式实现算法。

4.1 上下行链路的SINR对偶性

如果将多个协作基站视为一个虚拟的超基站，则多小区协作系统可以视作包含一个虚拟超基站和K个用户的虚拟多用户通信系统。文献[13]和文献[14]的研究表明，对于每一个用户k，上下行链路采用相同的波束向量和总功率约束可以达到相等的 SINR。因此可以通过优化虚拟上行链路达到优化下行链路的目的。

值得注意的是，这里的虚拟超基站受单基站功率约束，而非总功率约束。因此传统的上下行链路对偶性需要进行扩展才能应用于本文的场景。文献[13]中所提对偶性的修正形式可以直接应用于本文场景，但其分布式实现需要基站间频繁交换信息，不满足有限协作的要求。为此，本文将提出协作多小区模型下的近似上下行链路对偶性，并以此为基础推导分布式协作波束成形算法。

首先将基于单基站功率限制的虚拟上行链路问题表示为如下形式

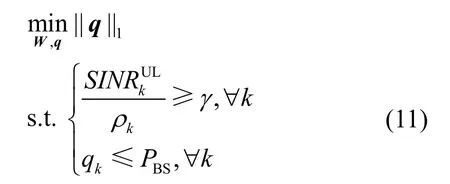
其中， q = [ q1,… ,qK]T为虚拟上行链路的功率向量，第k个用户的上行链路SINR为

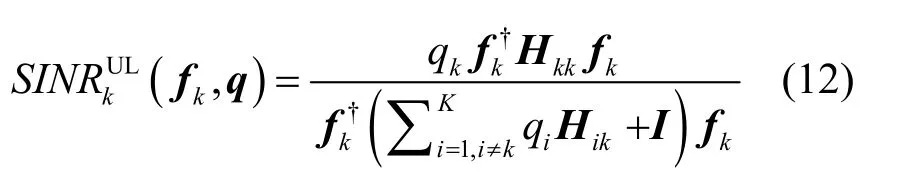
假定式(11)的解为 q*和 W*，通常有 || q*||1≤KPBS。传统的上下行链路对偶性原理表明：下行链路系统中可找到满足和功率为 || q*||1的下行功率向量利用该功率分配和波束成形 W*可使下行链路获得与虚拟上行链路相等的最大化最差SINR值。仿真结果进一步表明上述上下行链路功率分配向量通常满足即单基站功率约束下的多小区协作系统上下行链路存在近似的SINR对偶性。因此通过求解问题（11）可以近似得到问题（4）的解。下面将理论分析该结论。

首先定义

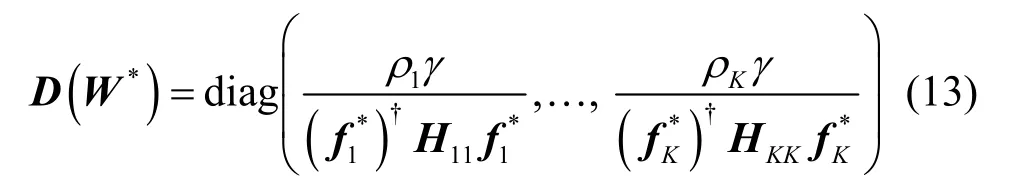
及矩阵 ψ （ W ） ，它的第 （i, j） 个元素表示为

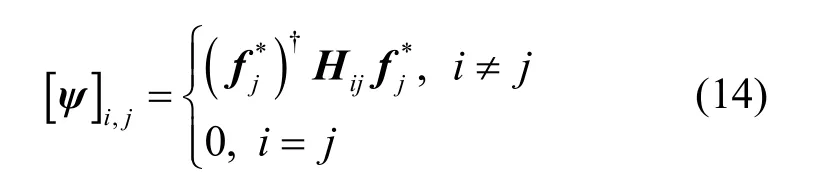
文献[14]表明上下行链路的功率向量均与如下矩阵有关

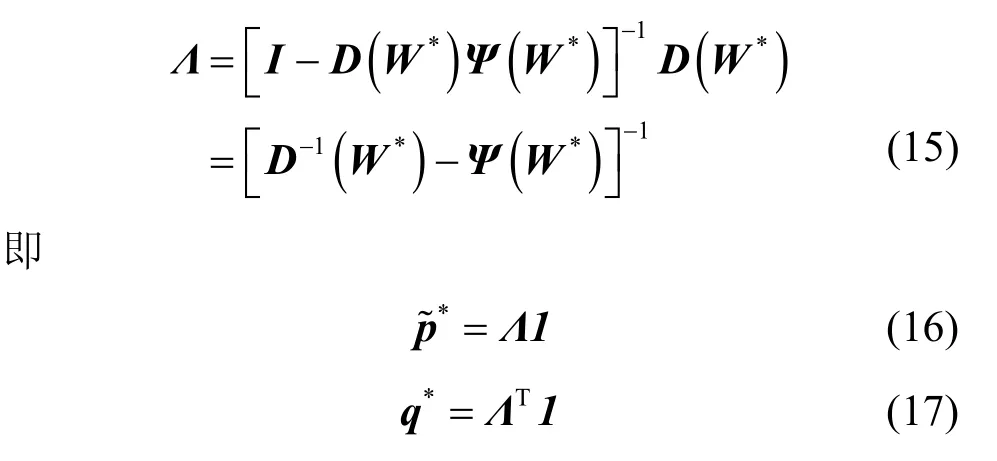
其中，1为全1向量。由以上2式可知，Λ为对角矩阵时有*=˜pq，即此时单基站功率约束下的对偶性原理精确成立。以此类推，上述对偶性原理的近似程度可由Λ的对角占优特性来指示。下面的分析将证明Λ为对角占优矩阵，并且在接收端 SNR极大或极小时变为准对角阵。首先观察1-Λ 并据下式度量[15]判断其是否为对角占优矩阵：

若对于任意k，均有ηk＞1，则Λ-1为严格对角占优阵。由于为问题(13)的解，故

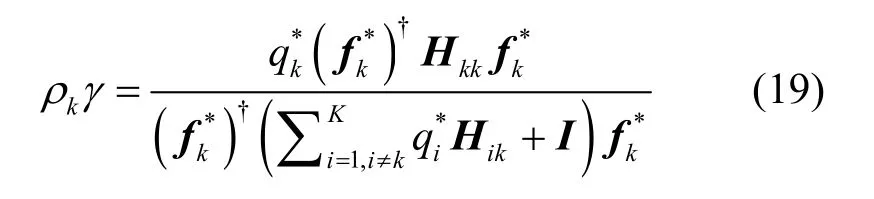
基于此，kη可以进一步写为

由于动态组建的协作多小区系统注2注2 协作基站/小区簇动态组建策略是根据用户的信道条件动态地选择多个基站和多个用户，被选中的每个用户与被选中的多个基站之间的信道强度通常具有同一数量级。中的值通常具有相同的数量级，故可近似得到ηk＞ 1 ,∀k 。特别当接收 SNR值极小时，即易知ηk远大于1，即Λ-1为准对角阵。同样，当接收SNR值极大时，用户间干扰的数量级将大于噪声方差。因此求解问题(11)得到优化波束成形向量的主要作用是消除用户间干扰，故有可得ηk远大于1。综上可知，对于给定的可达γ值， Λ-1和Λ均为对角占优矩阵，表明单基站功率约束下的上下行链路对偶性在大概率意义上近似成立，本文第5节的仿真结果进一步验证了这一结论。

4.2 分布式解决方案

利用上面给出的上下行链路近似对偶性原理，将提出一种很逼近第3节中集中式优化算法性能的分布式迭代求解算法。基本思路是先进行虚拟多小区上行链路波束成形协作优化，然后基于对偶性原理获得下行链路的优化波束成形向量和下行功率向量。对应的虚拟上行链路优化问题可写为

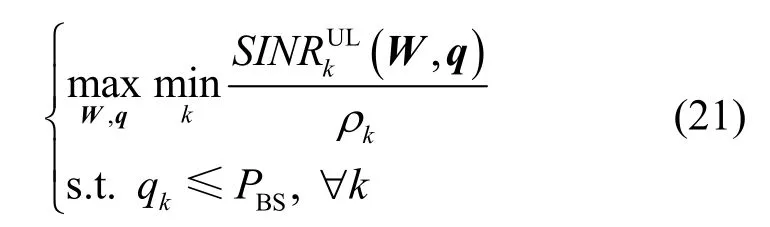
为解决该虚拟问题，利用定点迭代算法[16]提出一种低回程开销的分布式解决方案。具体算法描述如下：

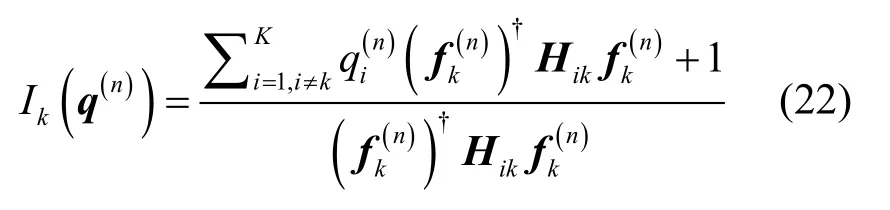
其中，

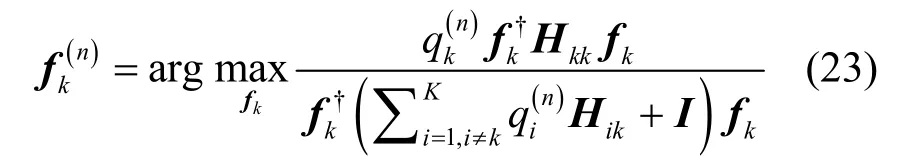
附录 A将证明上面迭代算法能有效解决问题(19)，其解记为由上下行链路存在的近似对偶性原理可知，下行链路的优化波束成形向量即为优化功率分配向量计算如下：

需要指出的是，由于单基站功率约束下的上下行链路对偶性只近似成立，因此某些情况下（很小的概率）可能略大于 PBS，但仿真结果表明，由此产生的性能损失很小。

4.3 协作开销

下面将分析所提分布式算法的协作开销。由式(5)可知，第二优化步骤中各基站仅需本地信道信息即可迭代更新发射波束形成向量；第一优化步骤所提迭代算法中，由于迭代步骤2)中gk（n）简单计算为并不改变最终结果，因此算法实施时无需计算 γ（n），故虚拟上行链路中用户k的功率分配向量和波束成形向量可以分布式地迭代更新，该过程需各基站共享每次迭代得到的功率向量 q（n），因此在第n次迭代中，基站k需广播其功率值至其他基站。若所提算法收敛于第(N+1)次迭代，则基站间需交换NK个正值参数。实际系统中，交互参数需进行量化后传输，由于的取值限于[0 , PBS]内，故可以简单地采用均匀线性量化器对参数进行量化。

另外，由式(24)可知，为计算p，各基站需知道D和Λ，因此需要基站间交换D和Λ的非零元素，共需要交互 K2个正实参数。

综上所述，算法实施(N+1)次迭代需在基站间交互 N K + K2个正实参数。仿真结果显示，当K= 2 和 K = 3 时算法收敛通常只需5次左右的迭代，且单次迭代( N = 0 )即可获得非常接近算法的收敛性能。表明所提分布式解决方法只需非常有限的基站间回程开销即可获得逼近Pareto最优的性能。另外需要指出的是，如果直接通过基站间共享信道状态信息进行协作波束成形设计，每个基站获取非局部 CSI共需22MK个实参数的回程交互量，该开销在实际系统参数设置下远大于所提算法所需的回程开销，且随着天线数M线性增长，而所提分布式算法的回程开销并不随天线数明显增长，尤其适用于天线数目较多的多小区协作系统。

5 仿真结果

本节将通过计算机仿真考察所提算法的性能。主要考虑2基站协作和3基站协作的场景, 相邻协作基站间距离为1km。由于协作系统中用户通常均位于小区边缘，仿真中考虑用户距服务基站的距离为400m，距其他协作基站的距离为600m。

假设平坦信道衰落模型，信道矢量 hki表示为其中为快速衰落信道，服从CN（0,I ）分布；μki为大尺度衰落，计算如下

其中，β为扩展系数，l为路径损耗的指数因子（通常l＞2），dki为用户k和基站i间的距离。χki表示服从对数正态分布的阴影衰落。信道仿真时大尺度路径损耗计算为 3 8lg （ dki）+ 3 4.5（dB）[17]，阴影衰落的标准差为8dB。10Mbit/s带宽上的噪声系数为9dB。为与实际系统参数保持一致，仿真结果图中用10M总带宽上的发射功率表征系统的信干噪比。假设噪声功率谱密度为-174dBm/Hz, 则用户端在2基站和3基站场景下平均信干噪比(dB)与发射功率(dBm)的对应关系可计算如表1所示。

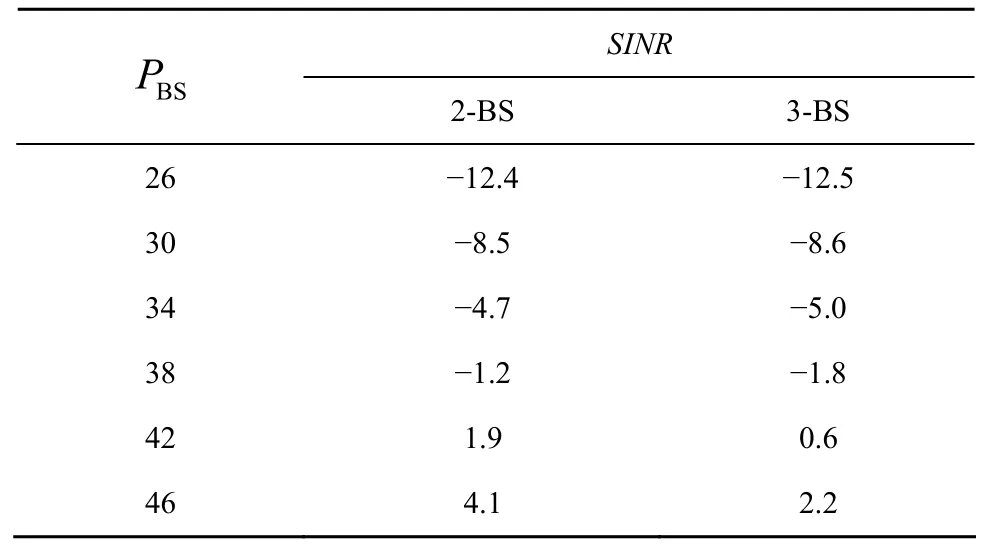
表1 PBS与平均SINR的对应关系

为考虑所提方法在基站间极有限信息交换情况下的系统性能，同时仿真了所提分布式算法经过单次迭代的系统性能，此时小区间仅需共享矩阵D和Λ中的非零元素。作为对比，本文还仿真了基于 SGINR准则[8,9]的多小区分布式波束成形系统的性能。

图1和图2给出了（M , K ）= （ 4, 2）参数配置下，2种典型随机信道下多小区协作波束成形系统的帕累托界[2]。图中同时给出了所提算法和SGINR算法得到的多用户速率集合的位置，表明本文所提集中式算法和SGINR算法得到的速率集合均位于帕累托界上。但图1显示，与SGINR算法不同，集中式算法得到的速率集合恰好位于帕累托界和直线 y=x的交叉点。在图2所示的另一种典型场景下，帕累托界和直线 y=x并无交点，此时集中式算法得到的速率集合为帕累托界距离直线 y=x最近的点。由于本文所采用的是近似的上下行链路对偶性，故分布式算法与集中式相比有一定的性能损失；然而，所提分布式算法的最差速率性能均优于SGINR算法。

图1 一次随机实现信道条件下的协作波束成形多小区下行系统的用户速率以及帕累托界， PBS= 4 0dBm ，(M , K) = (4, 2)

图2 另一次随机实现信道条件下的协作波束成形多小区下行系统的用户速率以及帕累托界， PBS=40dBm, (M , K) = (4, 2)

本文所提算法基于单基站功率约束的上下行链路对偶性，因此有必要考察上下行链路对偶的精确性。第4.1节的分析表明，只要满足就可以保证它的有效性；反之，所提分布式算法将会有一定的性能损失，其大小取决于超出功率约束部分的大小。下面定义如下的功率溢出比φ，并对其进行计算机仿真。

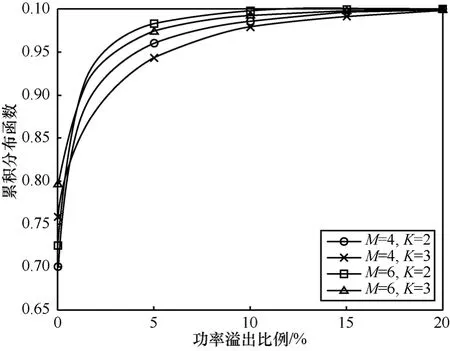
图3 分布式优化结果中下行链路功率分配向量中功率溢出比例的累积分布函数， PBS=40dBm

图4、图5分别仿真了所提算法和SGINR算法中最差用户的平速率性能。仿真结果表明在所有配置（M , K ）= ｛ （4, 2）,（6, 2）,（4, 3）,（6, 3）｝ 中，特别是在较高信干噪比和K=3的情况下，本文所提分布式算法均优于SGINR算法。另外需要指出的是，所提迭代算法经过单次迭代即可获得算法收敛的绝大部分性能，多次迭代后相比单次迭代的性能增益非常有限。该结果表明，只需极其有限的协作就可以保证所提分布式算法的有效性。仿真结果同时显示，所提分布式算法的性能非常逼近集中式算法。如前所述，本文所提集中式算法可以达到帕累托界的性能，这表明本文所提分布式算法可以在有限协作的情况下获得逼近帕累托最优的性能。

图4 协作波束成形多小区下行系统的最差用户平均速率( 2K= )

图5 协作波束成形多小区下行系统的最差用户平均速率( 3K= )

6 结束语

本文主要研究了单基站功率约束下公平性速率优化准则下的多小区下行链路协作波束成形技术。首先提出了一种2步优化的集中式算法，并证明了该算法可以达到帕累托界上最差用户速率最大化的点。然后，进一步利用单基站功率约束下近似的上下行链路对偶性设计了一种只需小区间交换有限参数的分布式算法。仿真结果表明本文所提算法可以在小区间仅进行有限协作的情况下达到逼近帕累托最优的性能。

附录A 分布式迭代算法收敛性证明

1) q(n)中每个元素在迭代过程中单调递减；

2) q(n)必收敛到唯一的最优点；

3) 定点迭代的任意中间结果 q(n)都能达到预定目标γ。

利用上述性质，下面证明第4.2节所提迭代算法的收敛性。从第n次迭代开始考虑，由步骤5)可知， q(n)满足单基站功率约束并可获得最小信干噪比 γ(n)（即可达到干噪比目标 γ(n)）。在接下来的第(n+1)次迭代中，由于 g（n+1）=I （ γ（n）, q（n）） 为标准的定点迭代过程，根据性质1)，可知

因此，在该次迭代步骤3)有1α≥。根据SINR的计算表达式可知

再根据 γ(n)的定义可知

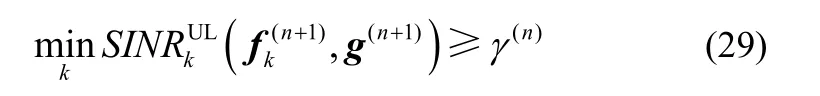
因此有 γ(n+1)≥ γ(n)，即最小 SINR在迭代过程中单调递减，迭代算法收敛到唯一定点。

[1] LARSSON E, JORSWIECK E. Competition versus cooperation on the MISO interference channel[J]. IEEE J Sel Areas Commun, 2008,26(7): 1059-1069.

[2] JORSWIECK E, LARSSON E, DANEV D. Complete characterization of the Pareto boundary for the MISO interference channel[J]. IEEE Trans Sig Process, 2008, 56(10): 5292-5296.

[3] SIMEONE O, SOMEKH O, POOR H. Downlink multicell processing with limited backhaul capacity[J]. EURASIP Journal on Advances in Signal Processing, 2009:840814.

[4] PAPADOGIANNIS A, HARDOUIN E, GESBERT D. Decentralising multi-cell cooperative processing on the downlink: a novel robust framework[J]. EURASIP Journal on Wireless Communications and Networking, 2009:890685.

[5] NG B, EVANS J, HANLY S. Distributed downlink beamforming with cooperative base stations[J]. IEEE Trans Inform Theory, 2008, 54(12):5491-5499.

[6] BJORNSON E, ZAKHOUR R, GESBERT D. Cooperative multicell precoding: rate region characterization and distributed strategies with instantaneous and statistical CSI[J]. IEEE Trans Signal Process, 2010,58(8): 4298-4310.

[7] DAHROUJ H, YU W. Coordinated beamforming for the multi-cell multi-antenna wireless system[J]. IEEE Trans Wireless Commun,2010, 9(5): 1748-1759.

[8] LEE B, JE H, SOHN I. Interference-aware decentralized precoding formulticell MIMO TDD systems[A]. Proc IEEE GLOBECOM[C]. 2008. 1-5.

[9] HASSANPOUR N, SMEE J, HOU J. Distributed beamforming based on signal-to-caused-interference ratio[A]. Proc IEEE ISSSTA[C].2008. 405-410.

[10] BENGTSSON M, OTTERSTEN B. Optimal and Suboptimal Transmit Beamforming[M]. Handbook of Antennas in Wireless Commun, L C Godara, Ed, CRC Press, Boca Raton, USA, 2001.

[11] WIESEL A, ELDAR Y. SHAMAI S. Linear precoding via conic optimization for fixed MIMO receivers[J]. IEEE Trans Sig Process,2006, 54(1): 161-176.

[12] HUANG Y, ZHENG G, BENGTSSON M. Distributed multicell beamforming with limited intercell coordination[J]. IEEE Trans Sig Process, 2011, 59(2): 728-738.

[13] YU W, LAN T. Transmitter optimization for the multi-antenna downlink with per-antenna power constraints[J]. IEEE Trans Sig Process, 2007, 55(6): 2646-2660.

[14] SCHUBERT M, BOCHE H. Solution of the multiuser downlink beamforming problem with individual SINR constraints[J]. IEEE Trans Vehicular Tech, 2004, 53(1): 18-28.

[15] HORN R, JOHNSON C. Matrix Analysis[M]. Cambridge, United Kingdom: Cambridge University Press, 1985.

[16] YATES R. A framework for uplink power control in cellular radio systems[J]. IEEE J Select Areas Commun, 1995, 13(7): 1341-1347.

[17] 3GPP TR25.996 V.8.0.0 Release 8. Spatial Channel Model for Multiple Input Multiple Output (MIMO) Simulations[R]. 3GPP, Tech Rep 2009.