多中继协同通信系统中基于循环正交训练序列的信道估计算法

张志鹏，钟杰，赵民建

（1. 浙江大学 信息与电子工程学系，浙江 杭州 310027；2.浙江省综合信息网技术重点实验室，浙江 杭州 310027）

1 引言

在深空通信中，无线信号微弱、且可能出现深衰落，使得通信链路难以建立或保持。另外，地面接收站接收的信号会因地面、山峦的反射而引入频率选择性衰落，进一步恶化传输的性能，进而限制了深空通信的可靠性，当信号带宽增大时频率选择性衰落的影响会更加明显。传统的端到端单天线系统抵抗深衰落以及多径的能力是有限的，很难满足深空通信的要求。一种解决办法是引入多天线技术（MIMO），其提供的分集增益可以有效地提升多径信道下传输的可靠性[1]。虽然多天线技术可以在相当程度上提高抗衰落性能，但是基于多天线的分集系统中采用了天线阵列，增大了深空探测器的尺寸，提高了成本，大大增加了其实现难度。为了克服这个缺点，可以考虑利用多个卫星中转地面站和深空航天器之间的信号，即引入基于多中继的协同通信系统[2]。基于多中继的协同通信系统利用分布在空间不同位置的终端天线相互协同，虚拟传统的基于多天线的分集系统，在不明显增加终端实现复杂度的情况下实现分集。基于多中继的协同通信系统作为分集技术的一种实现方式，吸引了众多研究者的关注。文献[3]给出了协同系统的速率和信道容量，文献[4]将信道编码技术（Turbo码）引入到协同通信系统中，提高抵抗频率选择性衰落信道的能力，文献[5]将空时编码（STBC）引入协同通信系统，可以提升分集增益，获得更好的传输性能。

中继的方式常见的有译码前传（DF）和放大前传（AF），前者的中继节点收到源节点信号先译码再重编码前传，后者的中继节点收到源节点信号进行固定增益放大后就前传。网络中各节点是否要选择中继协同传输、选取哪些中继节点以及何种中继方式是中继协同通信研究必须要解决的问题。而这些问题的解决离不开信道状态信息（CSI）的获得。文献[6]推导了中继通信中训练序列的功率分配准则，并给出了LS信道估计算法。文献[7]给出了放大前传模式下最优信道训练序列的设计方法，以及相应的LMMSE信道估计器。以上几种算法运算复杂度较高，文献[8]给出了一种多中继频分复用导频的方法，将各个中继转发的导频在频域上分开，并给出了低复杂度的LS和LMMSE信道估计器，但是该估计方法采用了内插来估计整体信道，当中继数量增加时信道估计精度急剧下降。

为了能更好地适应实际的协同通信系统，针对上面提到的信道估计方法的不足，本文提出一种低运算复杂度、高精度的信道估计方法。该方法基于具有循环正交特性的训练序列，多个中继对接收到的源节点的训练序列进行循环移位，在各个中继间构建具有良好正交特性的信道训练字。仿真表明，该方法具有较低的运算复杂度，估计过程时间短，需要的训练序列较少，估计精度较高且估计精度不会因中继数量的增加而迅速下降。

本文的第2节将介绍协同通信的系统模型，第3节将推导出新的信道估计算法，第4节将给出该信道估计算法的仿真结果，并加以分析，第5节是结束语。

2 系统模型

假定中继协同通信系统如图1所示，该中继系统中有一个源节点，M 个中继节点 Ri( i = 1,2,… ,M )，一个目的节点。为了突出分集增益是通过多中继协同获得的，假定每个节点都只有一根天线。一般情况下，源节点经过各个中继到达目的节点的传输时延是不同的。令经过第一个中继 R1的传输时延为t0，经过第i个中继的传输时延为 t0+τi，比经过第一个中继的传输时延大τi。简单起见，假定τM≥τM-1≥ … ≥τ2。

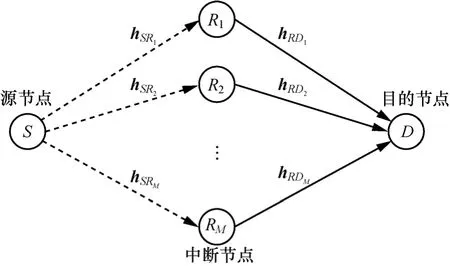
图1 中继协同通信系统模型

2.1 信道模型

离散多径信道可以用一个抽头延迟模型来表示。当系统采用块传输策略时，假定信道在一个符号块内保持不变，信道的最大多径延迟为L，则离散信道可以表示为

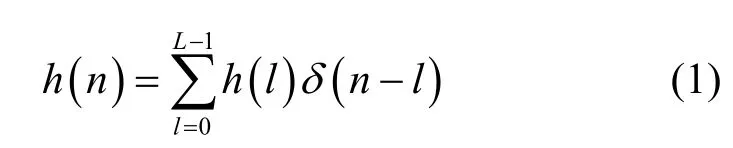
其中，l为某条路径传输延时，h （ l）为延时为l的路径的复数增益。表示为矩阵形式为 h =[h( 0),h (1),… ,h( L - 1 )]T。假定传输的符号块的长度为N，则信道的频率响应可以表示为

本算法中，考虑了经由各个中继的传输时延差，并将其作为中继-目的信道的一部分。经由第i个中继的传输时延差为τi，则该中继节点到目的节点的信道可以表示为 LRiD×1维的向量：

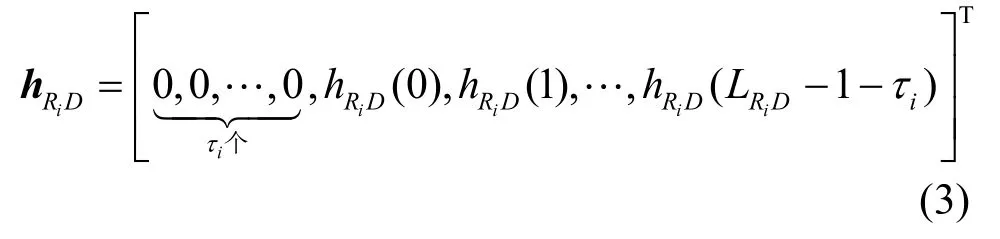
其最大多径延迟为iRDL 。则源节点到目的节点之间的总体信道为源-中继信道与中继-目的信道的线性卷积，即：

2.2 系统模型

中继协同通信的过程可以分成2个阶段。第1阶段是倾听阶段，该阶段源节点发送信号，各个中继节点接收来自源节点的信号。第2阶段是协作阶段，各个中继对第一阶段接收到的信号进行一定处理后转发[9]。如果采用放大前传模式，则只需对第一阶段的数据进行功率变换即可转发；若为译码前传，还需先对第一阶段的信号进行译码，重编码后才能发送。此处采用复杂度较低的放大前传模式，且假定第一阶段源节点发送的信号不会被目的节点接收，即源节点和目的节点之间不存在直传链路。

在第1阶段，源节点发送的信号为 x （ n），则第i个中继上接收到的信号为

其中， wi( n)表示第i个中继上的加性白高斯噪声。

在第2阶段，各个中继节点将接收到的信号乘以一个放大系数后，向目的节点转发。第i个中继的放大系数为αi。假定理想频率同步，则目的节点收到的信号为

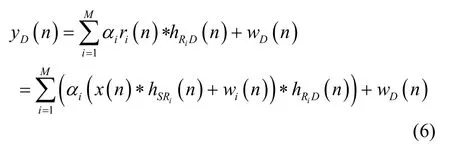
如上所描述的系统，中继通信的信道信息由 2部分组成。一是源到中继的信道信息（S-R CSI），二是中继到目的节点的信道信息（R-D CSI）。在估计信道信息时，可以分别估计出 S-R CSI和 R-D CSI，但是对于放大转发的中继方式来说，这样做的必要性不大。首先中继节点不对数据信息进行译码，因而不需要利用 S-R CSI；其次估计出的 S-R CSI还需经过R-D信道传输，降低了传输效率；再次中继节点进行信道估计还会增加中继节点的复杂度以及功率消耗。因而，此处只需估计出整体中继信道（S-R-D CSI）iSRDh 即可。

从系统模型可以看出，如果要独立地估计出经由各个中继的S-R-D信道，关键在于在第2阶段中各个中继节点转发的信道训练序列能够被目的节点所区分，即要求各个中继转发的序列在时间上是不相关的。实现这种互不相关的特性已经有2种方法，最简单的是在时间上相互独立，即各个中继节点收到源节点的训练序列后，依次转发收到的训练序列至目的节点，这是时分(TDM)的方法；另一种方法是各个中继节点在频域上将收到的训练序列乘以梳状函数，加上CP后转发至目的节点，这是频分(FDM)的方法[8]。此处采用的方法是利用具有循环正交性的训练序列使得各个中继转发的信道训练序列互不相关，从而使目的节点能够独立地估计出经过各个中继的S-R-D信道。

3 传输方案与信道估计算法

3.1 传输方案

采用块传输策略，源节点发送的信号为 x( n)，其矩阵形式为 x =[x( 0),x( 1 ),… ,x( N -1)]。信号 x ( n)前有长度为 LC≥Lm的循环前缀，则线性卷积可以转化成圆周卷积的形式，则在第i个中继上接收到的信号为

在第 2阶段，第i个中继对接收的信号移除 CP后，恢复出长度为N的序列，之后对恢复出的序列进行(i - 1 )L个符号的循环移位。得到的新序列表示为

在新序列 yi( n)前插入长度为 LC的CP，乘以放大系数αi后转发到目的节点。由于本算法将各个中继的传输时延作为中继-目的信道的一部分，因而可以将目的节点接收的信号表示为

从式(9)可以看出，多个中继节点对接收到的训练序列进行不同的循环移位，等价于在源节点有多个天线发送了经过不同间隔循环移位的训练序列。

信道训练序列的传输和处理过程如图2所示。

扩展整体信道hSRiD长度至Lmax，即当LSRiD＜n≤Lmax时，有 hSRiD（n）= 0 。则目的节点接收的信号可以表示为如下矩阵运算：

3.2 信道估计算法

图2 信道训练序列的传输和处理过程

信道的LS(least square)估计值为ˆh。则该信道估计值的误差代价函数可表示为

最小化式（12）中的代价函数，求J关于ˆh的导数，令其结果为0，则有

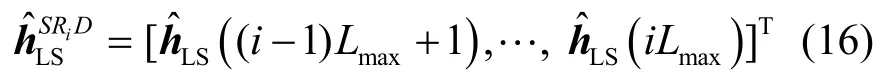
3.3 训练序列设计

若式(15)所示的估计误差取得最小值，需要满足[10]

若要满足式(18)，训练序列需满足 2个条件，一是序列 x ( n)与其循环移位的序列 ( x( n ) )N,LD在其最大多径延迟 Lmax内的相关特性为一单位冲激函数二是循环移位间隔超过L的序列之间相关值为0。即：

或者更加严格的，将上述条件写成：

称这种序列为等幅零互相关(CAZAC, constant amplitude zero auto correlation)序列。该序列的一种表达式为

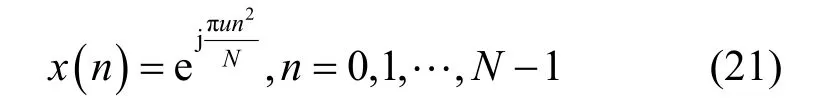
其中，u为与N互质的任意正整数。

4 性能仿真

本节将仿真在2个中继和4个中继的情况下，上述基于循环正交序列的信道估计方法的 MSE性能。循环正交序列采用 CAZAC序列，并与 TDM和FDM信道估计的MSE性能对比。此外，利用上述LS信道估计和LMMSE信道估计仿真中继系统的误码率（BER）性能，并与利用理想信道信息下的BER作对比。

仿真利用的信道是准静态的瑞利多径信道，S-R和R-D间信道最大延迟均为5μs，则S-R-D信道最大延迟为10μs。符号速率设为5MHz，FDM方法中训练序列的长度为 256，为降低 TDM 方法的时间开销，TDM方法中训练序列的长度为256/M，M为中继的数量。上述各种方法的CP长度均为32。数据传输采用OFDM，每个数据符号块包含256个子载波。为方便仿真，仅在目的节点上加噪，将目的节点的信噪比作为整体的信噪比。

从图3和图4中可以看出，LMMSE信道估计性能要优于LS信道估计。将本文提出的信道估计方法与TDM方法作对比，其时间开销基本一致时，TDM方法的MSE是本文信道估计方法的M倍。由于TDM方法采用的信道训练字长度为256/M，进行相关时能量为利用循环正交序列方法的1/M，因而TDM方法的估计性能更易受到噪声的影响，且估计误差随着中继数量M的增加而增大。而本文提出的利用循环正交序列的信道估计方法的误差不会随着中继的增加而增大，具有很好的稳定性。

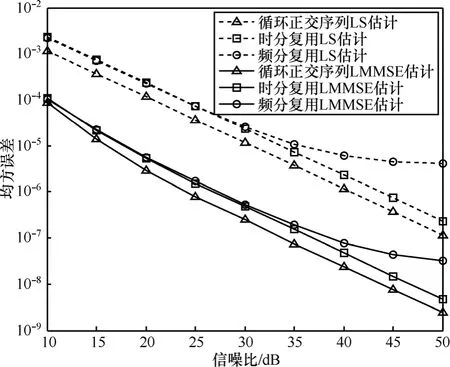
图3 2个中继时各种信道估计方法的均方误差性能

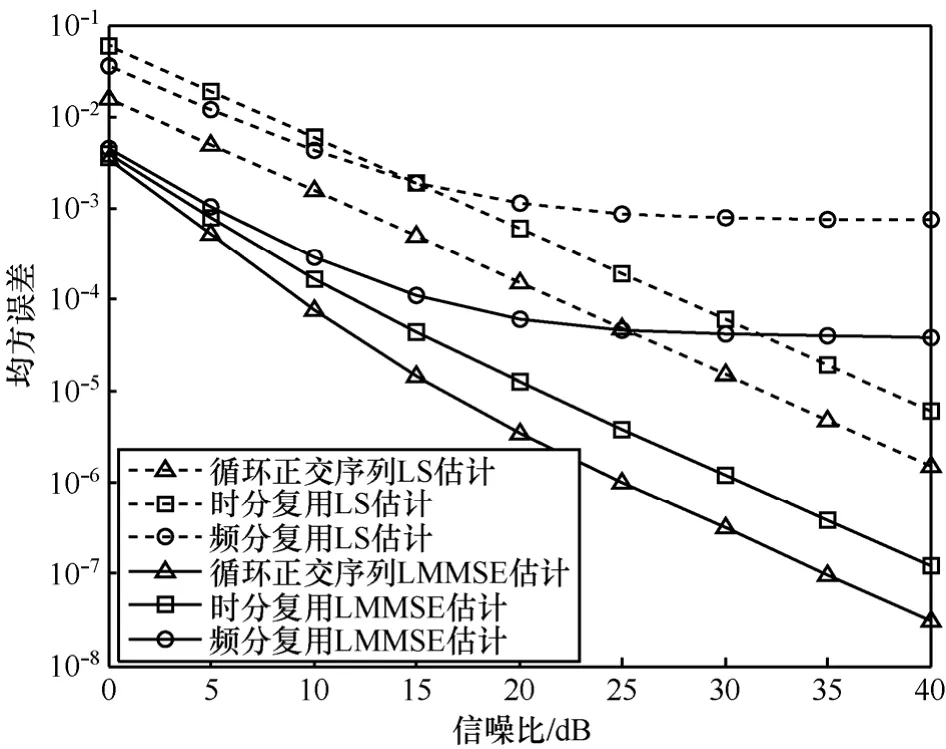
图4 4个中继时各种信道估计方法的均方误差性能

从图3和图4中可以看出，FDM方法存在估计误差平台，且当中继数量增加时误差平台上升，如图4所示当信噪比高于25dB时估计误差不再下降。这是由于FDM方法采用内插算法，而内插的误差会随着内插倍数M的增加而增大。本文提出的 LS信道估计的 MSE随着信噪比的升高持续降低，因而更加适用于较多中继的系统。

图5比较了2中继和4中继情况下，利用本文提出的LS和LMMSE信道估计结果与利用理想信道信息的BER性能。利用循环正交序列的LMMSE信道估计可以获得利用理想信道信息的BER性能，证明利用循环正交序列进行信道估计具有很高的估计精度。

图5 利用循环正交序列进行信道估计的系统误码率

5 结束语

本文分析了深空通信中应用多中继协同通信技术的意义，研究了多中继协同系统中基于循环正交训练序列的信道估计算法，推导了其LS信道估计和LMMSE信道估计，并获得了最优信道训练序列的设计准则。通过在各个中继上循环移位接收到的循环正交序列，可以消除各个中继转发序列之间的相关性，因而目的节点能分别估计出经由各个中继的整体中继信道。本文提出的信道估计算法运算复杂度较低，与已有的TDM方法和FDM方法仿真对比，本文提出的方法具有较高的估计精度和稳定性，且更加适用于具有较多中继节点的协同通信系统。利用本文提出的LMMSE信道估计的BER性能与利用理想信道信息的 BER性能基本一致。本文提出的多中继协同通信的信道估计算法在深空通信中具有较高的应用价值。

[1] ALAMOUTI S M. A simple transmit diversity technique for wireless communications[J]. IEEE Journal on Select Areas Commu, 1998,16(9): 1451-1458.

[2] NOSRATINIA A, HUNTER T E, HEDAYAT A. Cooperative communication in wireless networks[J]. IEEE Communications Magazine,2004,42(8): 74-80.

[3] SENDONARIS A, ERKIP E, AAZHANG B. User cooperation diversity part I and part II[J]. IEEE Trans Commu, 2003,51(11):1927-1948.

[4] HUNTER T, NOSRATINIA A. Coded cooperation under slow fading,fast fading and power control[A]. Proceedings of Conference on Signals, Systems and Computers[C]. 2002. 118-122.

[5] JING Y, HASSIBI B. Distributed space-time coding in wireless relay networks[J]. IEEE Trans Wireless Commu, 2006, 5(12):3524-3536.

[6] MAVROKEFALIDIS C, RONTOGIANNIS A A, BERBERIDIS K.Optimal training design and placement for channel estimation in cooperative networks[A]. Proc IEEE SPAWC[C]. 2010. 1-5.

[7] PANG J Y, SHEN G, WANG D Y, J et al. Channel estimation and optimal training design for amplify and forward MIMO relay channel under spatial fading correlation[A]. Proc IEEE VTC 2010-Fall[C].2010.1-5.

[8] YU X F, ZHAO C M, PAN C. Channel estimation based on pilot frequency division multiplexing for distributed space-frequency coded cooperative communication system[A]. Proc IEEE VTC 2010-Spring[C]. 2010. 1-5.

[9] EDFORS O, SANDELL M, VAN DE BEEK J J, et al. OFDM channel estimation by singular value decomposition[J]. IEEE Trans Commu,1997,46(7): 931-939.

[10] TUNG T L, YAO K, HUDSON R E. Channel estimation and adaptive power allocation for performance and capacity improvement of multiple-antenna OFDM systems[A]. Proc IEEE SPAWC[C]. 2001. 82-85.