基于计数布鲁姆过滤器的集合调和算法

田小梅，张大方，谢鲲，胡灿，杨晓波，史长琼,3

(1. 湖南大学 信息科学与工程学院，湖南 长沙410082; 2. 湖南环境生物职业技术学院 信息技术系，湖南 衡阳421005；3. 长沙理工大学 计算机与通信工程学院，湖南 长沙410114)

1 引言

在分布式系统中，假定2节点A、B分别拥有数据集合SA、SB，节点A和B进行数据交换得到并集SA∪SB的过程称集合调和[1]。也就是说，集合调和是通过分布式节点进行数据交换获得2节点数据集合并集的过程。集合中的元素可以是P2P系统中的文件块或路由协议中的链路状态分组标记等。集合调和在分布式文件分发、闲谈协议等分布式计算领域是一个重要的基本问题。一般说来，集合调和可以用于需要对无序分布式数据维护一致性的任意系统中。集合调和已广泛应用于分布式数据库与文件系统[2]、信息安全[3,4]、闲谈协议[5]、移动数据库同步[6]、资源定位系统[7]等领域。集合调和过程最关键的问题是如何高效计算集合差集的问题。集合调和中查找差集的技术亦可用于网络分布式系统中的去重过程，如数据域系统[8,9]和文件系统[10,11]，它们首先找出交集中的数据，删除重复数据并用指针代替，从而达到节约空间的目的。

很明显，完成集合调和的最直接方法就是节点B直接传输集合SB给节点A，节点A计算得到并集SA∪SB。在大规模系统中，集合SB数据量非常庞大，直接传输集合SB要消耗大量的带宽。因此，目前大多数方法都是先通过某种方法计算出差集 SB-SA，节点B仅传输SB-SA给节点A，从而节约了带宽使用量。其通常步骤如下：首先将集合SA使用某种数据结构表示，节点A传输该数据结构给节点B，节点B计算出差集SB-SA，然后节点B传输SB-SA给节点A，节点A求出SA∪SB。在此过程中，集合SA的表示往往要求精简的数据结构来表示。通常，为节约带宽和减少网络延时，在分布式系统中，集合调和时传输消息比特数及数据交换轮数往往要求尽可能低。这是分布式系统进行集合调和的最基本要求。

日志记录系统是另一类常见的集合调和方法，每节点额外维护一个具有时间戳的更新日志(log)，当需要调和时，节点B传输自上次调和以来的所有更新信息给节点A，节点A根据更新信息完成调和。日志记录系统由于维护开销大，会增加系统设计的难度，其应用范围得到一定的限制[12,13]。此类方法由于在调和前需要记录数据更新信息等背景知识(prior context)，可称为有状态集合调和(stateful set reconciliation)。本文将不借助日志记录等背景知识的集合调和方法称为无状态集合调和。无状态集合调和由于不需维护状态信息，可扩展性好，使用简单，更易于应用于各分布式系统。下文仅讨论无状态集合调和法。

目前，无状态集合调和方法可分为2大类：精确集合调和和近似集合调和。精确集合调和[1,6,14～17]能得到差集(SB-SA)的准确成员，但存在网络传输消息比特数大或消息交换轮数较多的缺点，如特征多项式集合调和法。近似集合调和[13,18,19]则只能得到SB-SA的大部分元素，但其优点是：仅需单轮数据交换。

首先，本文通过理论分析和模拟实验证实：计数布鲁姆过滤器的减运算能支持集合的差集查询。利用这一结论，本文提出一种基于计数布鲁姆过滤器的集合调和方法(如图1所示)，其具体过程如下：数据集合SA、SB分别用计数布鲁姆过滤器表示，节点A传送SA的计数布鲁姆过滤器表示给节点B，节点B利用计数布鲁姆过滤器减运算得到的过滤器，查询SB中的差集元素SB-SA，将得到的SB-SA返回给A，A然后计算SA∪SB，完成集合调和。使用基于计数布鲁姆过滤器的集合调和方法能找出所有差集(SB-SA)元素。基于计数布鲁姆过滤器的集合调和法既具有精确集合调和法能得到全部SB-SA元素的优点，也具有近似集合调和法仅需单轮消息交换的优点。

图1 基于CBF的集合调和

本文第2节简单介绍精确集合调和、近似集合调和方法。第 3节描述基于计数布鲁姆过滤器的集合调和方法。第4节是基于计数布鲁姆过滤器的集合调和的性能分析及模拟实验部分。第5节是结束语。

2 集合调和

集合调和在分布式系统中具有广泛的应用范围。在内容分发网络或P2P系统中，由于网络异构性和网络波动(churn)的普遍存在，既便各对等节点同时从服务器端接收相同内容，其所接收到的文件块也往往存在显著的差异，此时，充分利用对等节点之间的连接带宽，在对等节点间仅仅传输对方节点缺失的文件内容，实现知情内容分发[18]，可以提高下载速度、缩短下载时间。或者，由于覆盖网中网络连接的短暂性，服务器和对等节点间的连接断开，在此极端情况下，对等节点需要从其他对等节点获取剩余文件块。这些情况下，发送节点B若能找出接收节点A缺失的文件块，仅传送SB-SA中文件块给A，可以达到合理利用网络带宽、快速获取全文的目的。

2.1 精确集合调和

精确集合调和最直观的方法是节点B直接发送SB所有元素给节点A，设元素位串长度为len，此时需传输 O(|SB|len)bit消息[18]，本文称为完整集合传输法。如果改为传送关键字的有序列表(关键字列表传输法)，则可改善通信效率，仅需传输 O(|SB|log(u))bit消息。当|SB|、len或u值较大时，完整集合传输法或关键字列表传输法所需传输的消息比特数较大，将消耗较多的网络带宽，在实际系统中较少使用。

还有一种常用的精确集合调和方法是特征多项式插值法(CPISync, characteristic polynomials interpolation)[1]。设 d=|SA-SB|+|SB-SA|，集合 SA、SB分别用特征多项式 CP(SA)、CP(SB)表示，节点 A、B各自对相同的(≥ d)个求值点进行多项式求值，得到最后进行插值与因式分解，恢复差集元素。使用特征多项式插值法进行集合调和，A节点仅需传送O(d×logu)bit数据消息给B节点，u为全集U的规模；在应用该法前，需将全集 U中所有位串(串长为len)映射为有限域Fq(q≥2logu)中的元素，且必须事先知道d的上界值，若未知，则必须通过A、B之间的多轮消息交换估算出d的合理上界，其中消息交换传送的求值总数每轮递增c倍。此法需进行插值与因式分解，计算时间复杂度为Θ(d3)。文献[1]的作者后又改进了该特征多项式插值法，使其只需Θ(d)计算时间复杂度，但以A、B之间更多的消息交换轮数(O(logpd))为代价，其中p为划分系数[14]。一轮消息交换至少需一个 RTT(常为1.5s)，这种多轮消息交换在很多对时间要求较高的系统中是应该尽量避免的。

针对CPISync法在无法获知对称差大小时需多轮消息交换的缺点，文献[17]提出了一种基于布鲁姆过滤器的精确集合调和(BFESR, Bloom filter based exact set reconciliation)方法，首先使用2节点的布鲁姆过滤器估算出2集合的对称差规模，然后再运行CPISync算法。BFESR算法中，可用来估算对称差规模的方法有2种：内积法和准交集查询法[17]。使用BFESR方法，若调用一次CPISync算法不能调和成功，则增加一定的特征多项式值再次调用CPISync调和算法,直到得到准确的并集元素。由于 BFESR方法使用内积法或准交集查询法获取了对称差规模的大致范围，从而避免了文献[1]所用的试探法需大量试探次数(消息交换轮数)的缺点，仅需少量的消息交换次数即能实现集合调和。实验表明：大多数情况下仅需单轮消息交换即能成功，是一种调和效率高的精确集合调和方法。尤其值得注意的是，设准交集查询法估算出的对称差规模为d0，若首轮消息交换即在节点间传送(1+a)d0个特征多项式值，并选取合适的a值，则BFESR方法可使用单轮消息交换完成调和。如文献[17]的实验环境中，取a=0.05则能在单轮消息交换后完成调和。

文献[20]则提出了使用多个短的布鲁姆过滤器进行集合调和的方法。调和节点多次交换布鲁姆过滤器和数据元素直到2节点包含相同的元素为止。该方法与文献[18]中使用纠错码和布鲁姆过滤器的方法相比，具有较低的计算复杂度，但其代价是消耗较多的带宽及需要较多的消息交换轮数。

2.2 近似集合调和

近似集合调和方法通常的调和步骤如下：节点A传递集合 SA的近似表示(如散列后的集合(hash(SA))[18]、比特向量布鲁姆过滤器表示的集合(BF(SA))[18]或集合的近似调和树[19](ART(SA))等)给节点B，节点B据此查询SB中元素y是否包含在集合A的近似表示中，若查询结果为是，则判定y不属于差集SB-SA，若查询结果为否，则判定y属于差集SB-SA，节点B返回找到的SB-SA元素给节点A。

上述近似集合调和方法都存在如下可能：元素y( y ∈SB-SA)与元素x(x∈SA)的散列值或布鲁姆过滤器表示相同，从而B错误地判定 y ∈SA，以致不能得到SB-SA的所有元素。也就是说，这些近似集合调和方法在查询差集时都存在假阴性误判(false negatives)，即原本属于SB-SA的元素可能被判为不属于SB-SA。

最近，文献[13]提出了一种使用 Difference Digest结构的近似集合调和，本地节点传递由可逆布鲁姆过滤器(IBF, invertible Bloom filter)[21]组成的Strata estimator给远程节点，远程节点据此估算出对称差规模d值，并返回相应的可逆布鲁姆过滤器，本地节点对可逆布鲁姆过滤器减运算后得到的可逆布鲁姆过滤器译码，获取 SB-SA和SA-SB中的元素。该方法能以接近于1的概率使用单轮消息交换找出对称差元素，从而达到调和的目的，其传输消息比特数与 d log(u)成正比。这种方法与本文提出的方法都借助于布鲁姆过滤器减运算来完成调和，但Difference Digest法存在一定的调和失败率，而本文提出的方法则能确保调和成功。

通常，近似集合调和方法仅需1轮消息交换即可得到SB-SA的大部分元素。此时，尽管可以使用纠错码恢复其余未被找出的差集元素[18]，但该机制会增加实现难度及处理需求，从而其应用受到限制。

精确集合调和中的特征多项式插值调和法在事先能确定|SA-SB|和|SB-SA|大致值的情况下，仅需单轮消息交换即能找出所有差集元素，如不能事先确定d的近似值，则需多轮消息交换才能恢复差集元素。文献[20]中的精确集合调和方法由于需要多次交换布鲁姆过滤器结构，同样存在需要多轮消息交换的缺点。而基于布鲁姆过滤器的精确集合调和[17]虽然可通过参数的调整使得算法能以接近于1的概率使用单轮消息交换完成调和，但其无法保证 100%的一次插值成功率(即调用一次 CPISync插值算法即调和成功的概率)。近似集合调和过程尽管仅需单轮消息交换，但有少量差集元素会被遗漏。在不传递集合SA的完整形式且无法获知|SB-SA|或|SA-SB|的情况下，本文提出的基于计数布鲁姆过滤器的集合调和方法能做到使用单轮消息交换获得所有差集元素，不会产生遗漏。

3 基于计数布鲁姆过滤器的集合调和

3.1 计数布鲁姆过滤器

布鲁姆过滤器用于对集合进行简洁表示，支持元素的快速成员查询，同时带有一定的假阳性比率，即有一定数量的不在集合中的元素被判为属于该集合。标准布鲁姆过滤器[22]能支持元素的插入及成员查询，不支持元素的删除。标准布鲁姆过滤器由于使用比特向量表示元素集合，其中的单个比特只能取值0或1，0表示没有元素映射到该位置，1表示有元素映射到该位置，而不能表示有多少个元素映射到该位置。计数布鲁姆过滤器 (CBF,counting Bloom filter)[23]则用计数器向量代替标准布鲁姆过滤器的比特向量，计数器的长度为r，插入元素时将对应的k(k为散列函数个数)个计数器的值分别加1，删除元素时将对应的k个计数器的值分别减1。计数布鲁姆过滤器除支持集合元素的插入与查询外，还支持集合元素的删除操作。计数布鲁姆过滤器广泛应用于很多领域中，如：重复检测[24]、高速缓存系统[25]、网络测量[26]等。

在介绍使用计数布鲁姆过滤器减运算进行集合调和的新方法之前，首先探讨一下计数布鲁姆过滤器减运算的相关性质。

3.2 计数布鲁姆过滤器减运算

定义1 (同源计数布鲁姆过滤器) 对于全集U中的任意子集SA、SB，其计数布鲁姆过滤器表示分别为CBF(SA)、CBF(SB)，若它们使用的k个散列函数为同一组散列函数，计数器向量长度m相同，且计数器长度r相等，则称CBF(SA)、CBF(SB)为同源计数布鲁姆过滤器。下文讨论的均为同源计数布鲁姆过滤器。

定义 2 (计数布鲁姆过滤器的减运算)如图 2所示，对于计数布鲁姆过滤器CBF(U)，CBF(SA)与CBF(SB)，令 CBF(U)i，CBF(SA)i，CBF(SB)i分别为它们的第i个计数器，CBF(SB)与CBF(SA)减运算定义如下：

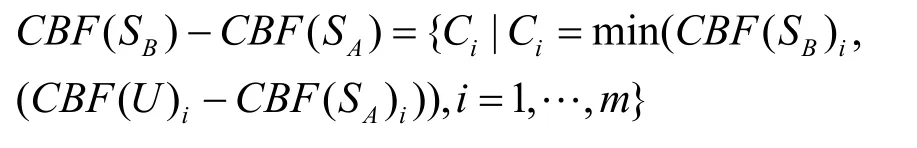
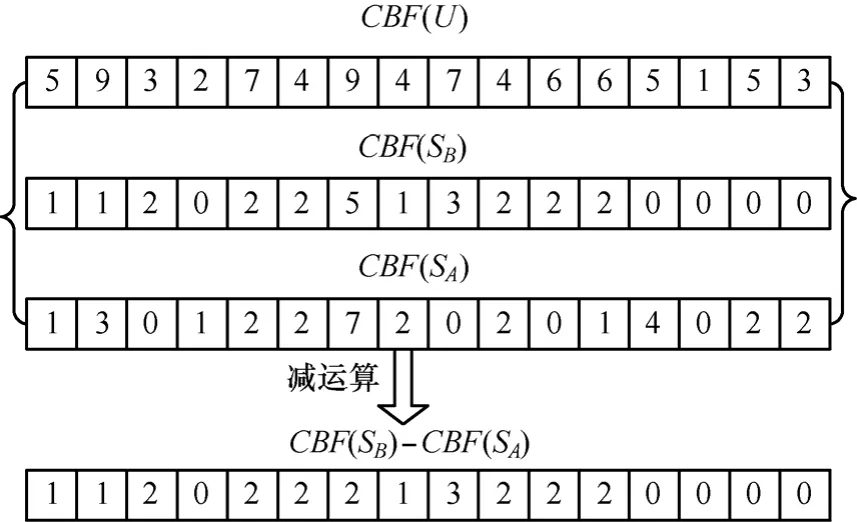
图2 计数布鲁姆过滤器减运算

定义3 (计数布鲁姆过滤器的大小关系) 2计数布鲁姆过滤器CBF(SA)与CBF(SB)，若∀i∈{1，…，m}，都有 CBF(SA)i≥CBF(SB)i，则称 CBF(SA)大于等于 CBF(SB)，记为 CBF(SA)≥CBF(SB)；若∀i ∈{1，…，m}，都有 CBF(SA)i=CBF(SB)i，则称CBF(SA)等于 CBF(SB)，记为 CBF(SA)=CBF(SB)；若∀i∈{1，…，m}，都有CBF(SA)i≤CBF(SB)i则称 CBF(SA)小于等于 CBF(SB)，记为 CBF(SA)≤CBF(SB)。

引理1 对于全集中的任意子集SA、SB，其计数布鲁姆过滤器表示分别为：CBF(SA)、CBF(SB)，若SA⊆SB，则必有CBF(SA)≤CBF(SB)。

证明 不失一般性，假设SA∩SB中元素先同时插入 CBF(SA)与 CBF(SB)中，此时 CBF(SA)i=CBF(SB)i，i=1,…,m；而后差集SB-SA中元素插入CBF(SB)中，因 SA⊆SB，SB-SA为空集或非空集，则CBF(SA)i≤CBF(SB)i，i=1,…,m，即 CBF(SA)≤CBF(SB)。引理得证。

定理 1 对于全集 U 中的任意子集 SA、SB，CBF(SA)、CBF(SB)分别为它们的计数布鲁姆过滤器表示，则 C BF( SB) - CBF( SA)≥ CBF( SB-SA)。

证明 若 C BF( SB-SA)i=Ci，1≤i≤m，因(SB-SA) ⊆SB，(SB- SA) ⊆，则据引理 1有：CBF( SB)i≥Ci且CBF()i≥Ci，1≤i≤m，又由计数布鲁姆过滤器的构造过程可知：CBF()i=CBF( U )i-CBF( SA)i)，从而可得：min(C BF( SB)i,(C BF( U )i-CBF( SA)i))≥ Ci, 1 ≤ i≤ m ,即(C BF( SB)-CBF( SA) )i≥ Ci, 1≤i≤ m ⇒ 若 C BF( SB- SA)i= Ci，则必有(C BF( SB)- CBF( SA) )i≥ Ci，1≤i≤m。

因此，(C BF( SB) - CBF( SA))≥ CBF( SB-SA)。定理得证。

推论1 使用CBF减运算 C BF( SB) - CBF( SA)查询SB中的差集SB-SA元素时能找出所有SB-SA元素，即CBF减运算 C BF( SB) - C BF( SA)查询差集时不存在假阴性误判。

证明 设 Q1、Q2分别为使用 C BF( SB)-CBF( SA)、 C BF( SB- SA)查询到的数据集合，由定理1可知，Q1包含Q2，又由于使用 C BF( SB- SA)查询 SB-SA时无假阴性但存在假阳性，即 Q2包含SB-SA，从而可得，Q1包含SB-SA。也就是说，使用CBF( SB) - C BF( SA)查询到的数据集合包含所有SB-SA元素，推论得证。

3.3 基于计数布鲁姆过滤器的集合调和

本文提出的基于计数布鲁姆过滤器的集合调和方法分为如下几个步骤。

Step1 节点A构造CBF(SA)，并将之传送给节点B。

Step2 节点B进行CBF减运算，得到过滤器CBF(SB)-CBF(SA)。

Step3 节点 B使用 CBF(SB)-CBF(SA)查询 SB中元素是否属于SB-SA，获得全部SB-SA元素及少量交集SA∩SB元素，并返回给节点A。

Step4 节点A将Step3中节点B返回的结果集与SA合并，得到完整的SA∪SB。

算法的Step 3中，节点B找出的结果集中包含SB-SA中全部元素，也包含少量SA∩SB中元素(其数量取决于CBF()的假阳性概率，参见定理3)，交集元素的少量冗余并不影响算法接下来的集合并运算(即Step 4)的结果。本文将这一方法称为基于计数布鲁姆过滤器的集合调和(CBFSR, counting Bloom filter based set reconciliation)。

首先定义调和率和冗余率，将二者作为评估调和算法性能的2个指标，然后在此基础上对CBFSR算法的性能进行理论分析。

定义4 (调和率)集合调和过程中，设 B返回给A的元素集合为Ssub，Ssub中SB-SA元素个数设为Srecon，Srecon与差集规模|SB-SA|的比率，称调和率(reconciliation ratio)。其计算公式为：

定义5 (冗余率)集合调和过程中，B返回给A的集合 Ssub中 SB∩SA元素个数设为 Sredun，Sredun与差集规模|SB-SA|的比率，称冗余率(redundancy ratio)。其计算公式为：

定理2 CBFSR法调和过程中，节点B在使用CBF(SB)-CBF(SA)查询 SB中元素是否属于 SB-SA时能找出所有SB-SA元素，其调和率为100%。

证明 1)若 x ∈ SB- SA，则CBF( SB)hj(x)≥1,j=1,…,k;2)x∈SB-SA→x∈ U ∩ x∉SA→(C BF( U )hj(x)-CBF( SA)hj(x))≥ 1, j = 1 ,… ,k。

由1)、2)及定义2得：

min(C BF( SB)hj(x),(C BF( U )hj(x)-CBF( SA)hj(x)))≥1, j = 1 ,… ,k即(C BF( SB) - CBF( SA) )hj(x)≥ 1, j=1,… ,k 。也就是说，只要元素 x属于 SB-SA，则CBF(SB)-CBF(SA)中对应x的所有计数器一定非0，从而判定x属于SB-SA，不会被判为不属于SB-SA。CBFSR法中节点B能找出所有SB-SA元素返回给节点A，其调和率为100%。定理得证。

定理 3 CBFSR法调和过程中，在使用CBF(SB)-CBF(SA)查询 SB中元素是否属于差集SB-SA时，会有少量不在 SB-SA中的元素(即少量 SA∩SB元素)被误判为属于SB-SA，即使用CBF(SB)- CBF(SA)进行差集查询时存在假阳性误判，SA∩SB中元素被误判为差集SB-SA元素的概率为CBFSR法的冗余率为100%。

证明

1) 若 x ∈SA∩SB，则必有：CBF( SB)hj(x)≥1,j = 1 ,… ,k ，此时只要CBF()hj(x)≥1, j = 1,… ,k，则必有min(C BF( SB)hj(x),(C BF( U )hj(x)-CBF( SA)hj(x)))≥1, j = 1 ,… ,k,即(C BF( SB) - CBF( SA) )hj(x)≥1,j=1,… ,k 。也就是说，使用CBF(SB)-CBF(SA)查询SA∩SB中元素是否属于SB-SA时存在假阳性，其假阳性误判概率fp与CBF()的假阳性概率相同，等于即查询过程的假阳性误判概率取决于与|SB-SA|、|SA∩SB|无关。

2)由1)可知，SA∩SB中有 fp|SA∩SB|个元素在 Ssub中，从而 CBFSR法的冗余率为定理得证。

4 性能分析与实验比较

4.1 性能分析

将本文的CBFSR算法与已有的5个调和算法进行性能的对比分析，用于比较的5个算法如下。

算法 1 使用比特向量布鲁姆过滤器的近似集合调和算法，本文将其称为BFSR(Bloom filter based set reconciliation)[18]法，其具体过程如下：节点 A传递比特向量布鲁姆过滤器表示的集合(BF(SA))给节点B，节点B据此查询SB中元素y对应的k个散列位置在BF(SA)中是否全为1，若是，则判定y属于SB∩SA，否则，判定y不属于SB∩SA。由于这一交集查询过程中存在少量假阳性，节点B仅能找出SB-SA大部分元素。最后，节点B返回这部分SB-SA元素给节点A，执行集合并运算SA∪(SB-SA)，得到SA∪SB的大部分元素，完成近似集合调和。

算法2 使用近似调和树的近似集合调和算法，本文称其为ART法，该算法中近似调和树的构造较为复杂，由于篇幅所限，算法具体步骤参见文献[19]。

算法 3 Difference Digest法[13]，Difference Digest结构由Strata Estimator和IBF 2部分组成。节点A首先发送其构造的Strata Estimator给对方节点B，B使用该 Strata Estimator估算出 d，构造出合适的IBF(B)返回给A，A使用IBF减运算计算出IBF(A)-IBF(B)，并对IBF(A) -IBF(B)进行译码得到SB-SA和SA-SB。

算法4 CPISync法，即2.1节介绍的特征多项式插值法，是一种精确集合调和算法，算法具体步骤参见2.1节介绍和文献[1]。

算法5 改进的CPISync法，是特征多项式插值法的一种改进算法，参见2.1节介绍和文献[14]。

表 1列出了上述 5种集合调和方法和本文CBFSR算法的性能分析结果。其中，节点间的传输消息比特数仅列出了节点A传送给节点B的消息比特数；对于节点 B返回给节点 A的消息比特数，CBFSR法为O(|SB-SA|+|SA∩SB|)，Difference Digest法为 O(|SA-SB|+|SB-SA|)，其他调和方法均为O(|SB-SA|)，各方法差别不大。

由于CBF用r位计数器代替BF的二进制位，CBFSR法调和过程中 A节点需传送给 B节点O(rm)bit信息，BFSR法仅需传送O(m)bit消息，其中 m为计数器向量大小或比特向量大小。设法中，当m/n值确定时，为保证SA∩SB中元素被误判为SB-SA中元素的可能性最小，需取k=ln2(m/n)。例，若m/n=6，则k取值4时，的假阳性误判概率值 fp近似最小，计算得其fp=5.61%。若r=4，CBFSR法中节点A需传送给节点B的消息比特数等于4m，由B返还A的元素集合中包含全部SB-SA元素，也包含大约5.61%的SA∩SB元素，即调和率为 100%，冗余率为而BFSR法A节点需传送给B节点mbit消息，但约有的 SB-SA中元素被遗漏，若 u=2|SA|=2n，则大约 5.61%的差集元素被遗漏，即调和率为94.39%。

表1 各集合调和方法性能分析

CBFSR法可以找出SB-SA中所有元素，调和率为100%；由于CBF可支持删除操作，因此CBFSR法适用于更新频繁的系统环境；与BFSR法比较，CBFSR法多一次CBF减运算，需要r(如r=4)倍于BFSR法的传输消息比特数及节点在首次与源节点或对等节点建立联系时需得到CBF(U)。

ART法调和率取决于校正系数和分支系数，达不到100%；而CBFSR法调和率始终为100%，但传输消息比特数是ART法的r倍。

Difference Digest法与本文提出的CBFSR法都借助于布鲁姆过滤器减运算来完成调和，但Difference Digest法存在一定的调和失败率，尽管该概率较小，在使用适当参数配置的条件下不超过O(d-k)[13]，而CBFSR法则能确保调和成功。

与调和率同样为 100%的特征多项式调和法(CPISync法和改进的CPISync法)相比，CBFSR法具有仅需单轮消息交换、计算简单的优点。

4.2 实验比较

在分布式网络系统中，为实现集合调和，精确集合调和法中的CPISync法和改进的CPISync法通常需要多轮消息交换，网络延时较高，本文实验不考虑此类需多轮消息交换的算法。BFSR法、ART法等近似集合调和法与 CBFSR法一样，只需单轮消息交换，模拟实验中考察了BFSR法、ART法、CBFSR法3种调和算法，在调和率、冗余率等方面对它们进行比较。

实验中全集规模u=20 000，子集规模|SA|= |SB|=10 000，散列函数个数k=6，CBF或BF向量大小m=80 000，|SB-SA|取值范围为[100，9 000]。实验结果取100次实验的数据平均值。

ART法中校正系数c取0或2，分支系数b取2或4。b=2时的近似调和树称二叉调和树，b=4的近似调和树则称四叉调和树。

由图 3可见，CBFSR法的调和率始终为100%，与|SB-SA|、u、k、m 等参数设置无关。BFSR法的调和率取决于 k、m 及|SA|的值，与|SB-SA|的取值无关，实验结果非常集中地位于期望值97.84%附近。在4种不同参数设置的调和树中，校正系数为0的二叉调和树的调和率最低，约为71.71%。校正系数为2的四叉调和树的调和率最高，约为97.71%，与BFSR法的调和率极为接近。由本文实验结果可看出，ART法的调和率与|SB-SA|的取值无关，取决于校正系数和分支系数，校正系数和分支系数越大，ART法的调和率越高，选取足够大的校正系数和分支系数，可使ART法的调和率趋近于1。

图3 调和率

BFSR法、ART法等近似集合调和方法不存在冗余率，只有 CBFSR法存在冗余，当全集规模与子集规模取值确定时，其冗余率随差集规模|SB-SA|不同而不同，其变化趋势如图 4所示。冗余率与|SB-SA|成反比，差集越大，冗余率越小。本实验中，当|SB-SA|达9 000时，冗余率仅为0.24%。但冗余率的大小除与|SB-SA|有关外，还取决于k、m、u和|SA|，当其他参数相同，而u值较大、|SA|较小时，冗余率会随之增加。当冗余率较大时，会造成较多的带宽浪费，而当u和|SA|值相差不大时，则冗余率小，从而带宽浪费较小。

图4 基于计数布鲁姆过滤器的集合调和冗余率

根据定理 3，CBFSR法调和过程中，交集(SA∩SB)中元素被误判为 SB-SA元素的概率与的规模(u-|SA|)有关，其期望值为在前述实验设置中，误判概率期望值为2.16%。图5中的直线为SA∩SB元素用CBF(SB)-CBF(SA)查询的假阳性期望值，曲线为差集规模取不同值时的误判实测值。由图5可见，实测值非常一致地集中于期望值附近，说明定理3的分析是正确的。

图5 CBFSR法交集元素被判为SB-SA元素的概率

由上述算法分析及模拟实验结果可得出基于计数布鲁姆过滤器的集合调和法在应用前需事先获得 CBF(U)，这一操作可以在节点首次加入网络时完成，节点与远程节点在调和时(可能是多次调和)不再需要此操作，从而该方法以较小的冗余率、传输消息数倍于BFSR等近似集合调和法为代价，使得节点间仅需单轮消息交换即能实现调和率达100%，是一种简单、可靠的调和方法。

5 结束语

本文首先通过理论分析和模拟实验证明：计数布鲁姆过滤器的减运算能支持集合的差集查询。利用这一结论，设计了基于计数布鲁姆过滤器的集合调和方法，数据集合用CBF表示，利用CBF减运算得到的新过滤器 CBF(SB)-CBF(SA)找出 SB中属于SB-SA的元素，完成集合并运算 SA∪(SB-SA)，得到SA∪SB，实现集合调和。研究结果表明，基于计数布鲁姆过滤器的集合调和法兼具已有集合调和方法的优点，其算法简单，节点间仅需一次消息交换就能找出所有差集元素，实现精确集合调和，支持集合元素的动态删除，适合于更新频繁的系统环境。

接下来的工作重点是将本文提出的基于计数布鲁姆过滤器的集合调和法更进一步应用于实际分布式系统，如分布式数据库与文件系统、闲谈协议、移动数据库同步等系统，并优化其性能。

[1] MINSKY Y, TRACHTENBERG A, ZIPPEL R. Set reconciliation with nearly optimal communication complexity[J]. IEEE Information Theory, 2003, 49(9): 2213-2218.

[2] DECANDIA G, HASTORUN D, JAMPANI M, et al. Dynamo:amazon's highly available key-value store[A]. Proceedings of the 21st ACM SIGOPS Symposium on Operating Systems Principles[C]. New York, NY, USA, 2007. 205-220.

[3] 付波, 李建平, 文晓阳. 基于集合调和的远程口令恢复方法[J]. 计算机应用研究, 2009, 26(6): 2113-2116.FU B, LI J P, WEN X Y. Remote password recovery using set reconciliation[J]. Application Research of Computers, 2009, 26(6):2113-2116.

[4] ELKOUSS D, MARTINEZ J, LANCHO D, et al. Rate compatible protocol for information reconciliation: an application to QKD[A].Proceedings of the Information Theory Workshop (ITW)[C]. 2010.145-149.

[5] GUO K, HAYDEN M, VAN RENESSE R, et al. GSGC: An Efficient Gossip-Style Garbage Collection Scheme for Scalable Reliable Multicast[R]. Cornell University, 1997.

[6] STAROBINSKI D, TRACHTENBERG A, AGARWAL S. Efficient PDA synchronization[J]. IEEE Transactions on Mobile Computing,2003, 2(1): 40-51.

[7] VAN RENESSE R. Scalable and secure resource location[A].Proceedings of the International Conference on System Sciences[C].2000. 1530-1605.

[8] Data domain[EB/OL]. http://www.datadomain.com.

[9] ZHU B, LI K, PATTERSON H. Avoiding the disk bottleneck in the data domain deduplication file system[A]. Proceedings of the 6th USENIX Conference on File and Storage Technologies[C]. San Jose,California, 2008. 1-14.

[10] KULKARNI P, DOUGLIS F, LAVOIE J, et al. Redundancy elimination within large collections of files[A]. Proceedings of the Annual Conference on USENIX Annual Technical Conference[C].Boston, MA, 2004.

[11] BOLOSKY W J, CORBIN S, GOEBEL D, et al. Single instance storage in Windows 2000[A]. Proceedings of the 4th Conference on USENIX Windows Systems Symposium[C]. Seattle, Washington, 2000.

[12] BYERS J W, LUBY M, MITZENMACHER M. Accessing multiple mirror sites in parallel: using Tornado codes to speed up downloads[A]. Proceedings of the IEEE INFOCOM 1999[C]. New York, NY , USA 1999. 275-283.

[13] EPPSTEIN D, GOODRICH M T, UYEDA F, et al. What's the difference?efficient set reconciliation without prior context[A]. Proceedings of the ACM SIGCOMM 2011[C]. Toronto, Ontario, Canada, 2011. 218-229.

[14] MINSKY Y, TRACHTENBERG A. Practical Set Reconciliation[R].BUECE 2002-01. Boston University, 2002.

[15] MINSKY Y, TRACHTENBERG A. Efficient Reconciliation of Unordered Databases[R]. TR1999-1778. Cornell University, 1999.

[16] AGARWAL S, CHAUHAN V, TRACHTENBERG A. Bandwidth efficient string reconciliation using puzzles[J]. IEEE Transactions on Parallel and Distributed Systems, 2006, 17(11): 1217-1225.

[17] TIAN X M, ZHANG D F, XIE K, et al. Exact set reconciliation based on Bloom filters[A]. Proceedings of the International Conference on Computer Science and Network Technology[C]. Harbin, China, 2011.2001-2009.

[18] BYERS J, CONSIDINE J, MITZENMACHER M, et al. Informed content delivery across adaptive overlay networks[J]. ACM SIGCOMM Computer Communication Review, 2002, 32(4): 47-60.

[19] BYERS J, CONSIDINE J, MITZENMACHER M. Fast Approximate Reconciliation of Set Differences[R]. BU Computer Science TR 2002-19.Boston University, 2002.

[20] SKJEGSTAD M, MASENG T. Low complexity set reconciliation using Bloom filters[A]. Proceedings of the 7th ACM ACM SIGACT/SIGMOBILE International Workshop on Foundations of Mobile Computing[C]. San Jose, California, 2011. 33-41.

[21] EPPSTEIN D, GOODRICH M T. Straggler identification in round-trip data streams via newton's identities and invertible Bloom filters[J]. IEEE Transaction on Knowledge and Data Engineering, 2011, 23(2): 297-306.

[22] BLOOM B H. Space/time trade-offs in hash coding with allowable errors[J]. Communications of the ACM, 1970, 13(7): 422-426.

[23] FAN L, CAO P, ALMEIDA J, et al. Summary cache: a scalable wide-area web cache sharing protocol[J]. IEEE/ACM Transactions on Networking(TON), 2000, 8(3): 281-293.

[24] WEI J, JIANG H, ZHOU K, et al. Detecting duplicates over sliding windows with ram-efficient detached counting Bloom filter arrays[A].Proceedings of the 6th IEEE International Conference on Networking,Architecture and Storage[C]. 2011. 382-391.

[25] AHMADI M, WONG S. A Cache architecture for counting Bloom filters:theory and application[J]. Journal of Electrical and Computer Engineering,2011, (1): 1-10.

[26] 吴桦, 龚俭, 杨望. 一种基于双重Counter Bloom Filter的长流识别算法[J]. 软件学报, 2010, 21(5): 1115-1126.WU H, GONG J,YANG W. Algorithm based on double counter Bloom filter for large flows identification[J]. Journal of Software, 2010,21(5):1115-1126.