一种新的二叉树结构XML编码方案

桑俊霞，陶宏才

（ 西南交通大学信息科学与技术学院，成都610031）

随着XML文件的广泛使用，对XML的研究越来越多，包括XML编码、XML查询、XML存储等。其中XML编码可以有效地支持XML查询中的结构连接操作，是判断节点间结构关系的重要依据。

目前已有的编码方案主要分为2类：区域编码和前缀编码。

区域编码[1~2]是按照结点的物理位置进行编码，编码结构为，其中start和end分别表示节点的开始位置和结束位置。区域编码是目前使用较多的XML编码方法，但其不能有效地支持文档更新，虽然通过预留编码空间等方法缓解了它对文档更新的缺憾，但仍不够灵活。前缀编码[3~4]把节点路径做为编码依据，保存了编码的路径信息，编码支持文档更新，缺点是编码较长，占用存储空间较大。文献[5]提出了PBiTree编码，并在此基础上提出了基于横向拆分和基于纵向拆分的结构连接算法，该算法采用了二叉树编码方法，但算法复杂，中间转换较多，仍不够完善。文献[6]等提出的高效查询编码方法，采用记录节点路径的方式，支持快速查询操作，但需要较多的辅助信息。

本文提出了一种基于二叉树的BTB（Binary Tree Based，BTB）编码，编码是二进制格式，可以保存节点的路径信息。由于采用的是二进制的编码形式，有效地节省了编码的存储空间，并支持文档更新。

1 编码方法

BTB编码是基于树结构的编码，编码时需要用到完全二叉树结构。

1.1 XML文档树的二叉树化

XML文档是一种半结构化数据，可以以树的形式表示，该树被称为XML文档树。一棵XML文档树如图1，其中节点S是二叉树的根节点，即XML文档树的文档节点，最低层的6个节点是叶子节点。

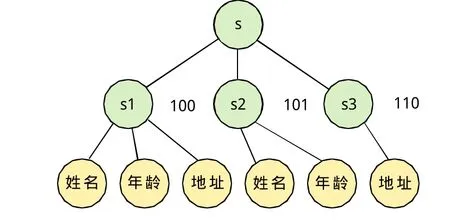
图1 XML文档树

BTB编码的编码思想是：把XML文档树二叉树化，对转化后的文档二叉树进行编码。把一棵XML文档树T二叉树化，转化后的二叉树用T′表示。二叉树化的步骤如下：

（1）T'的根节点为T的根节点N；

（2）对于其它节点，若它和它的所有兄弟加起来的节点个数n不大于2，则将其子节点作为T'中根节点的子节点；否则转到步骤（3）；

（3）以当前节点的双亲节点作为祖先节点，将当前节点及其兄弟节点下移[Ilog2nJ] －1层，中间以虚节点填充；

（4）重复步骤（2）和步骤（3），直到所有节点都处理完。

例如，图2是将图1中XML文档树二叉树化后的结果。

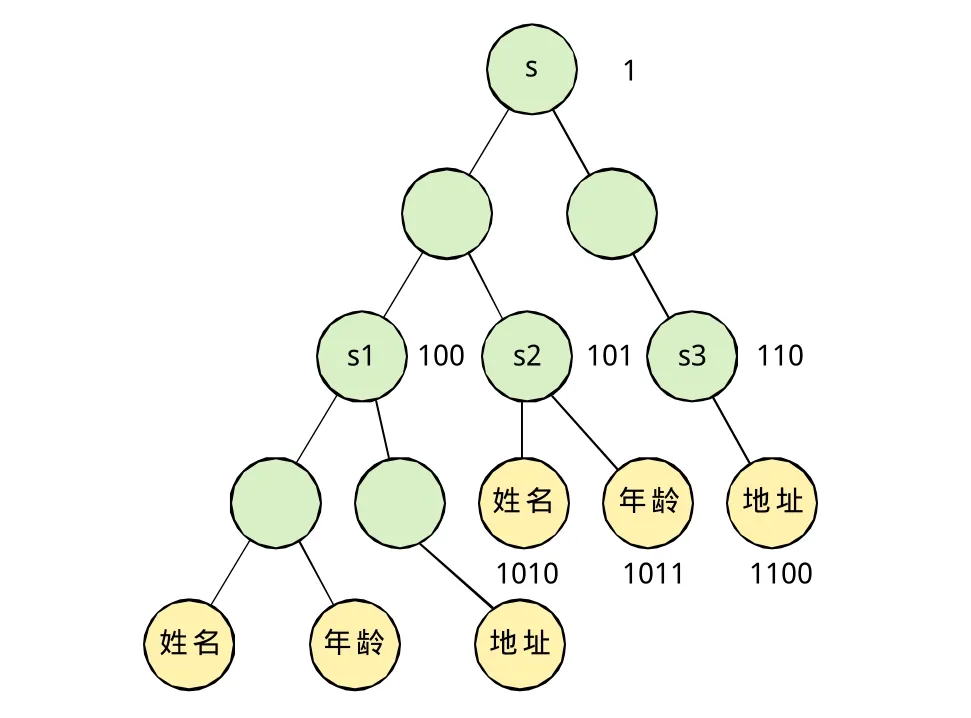
图2 嵌入完全二叉树的结果

1.2 BTB编码方法

对一棵文档二叉树进行编码，编码采用二进制表示，每个节点编码的二进制位数等于该结点所在的层数，根结点的编码为“1”，其它节点的编码为：双亲节点编码×2＋0/1。其中0和1分别表示左子树和右子树。

把一棵XML文档树二叉树化之后，对该二叉树进行编码。编码必须满足以下2点：

（1） 如果当前节点是根节点，编码为1；

（2） 如果当前节点不是根节点，当前节点u的编码由下式计算

L(u)=2×lv+x

其中lv为u的双亲节点编码。x的取值为0或1，当v是左子树时取0，v是右子树时取1。该编码方法称为BTB编码。

例如，图2中，节点S为根节点，编码为“1”，s1编码为“100”，s2的子节点姓名编码为s2的编码+“0”，即为“1010”。

编码是一个二进制串，每一个二进制位保存一个路径分支信息。存储时可直接按此二进制串表示的整形数据存储。BTB为不等长码，节点在树中的层数越小，编码长度越短；反之，越是处在下层的节点编码长度越长。有一些节点是在XML文档树中不存在的，是一些虚拟的节点，在编码时，可直接跳过。

对一棵XML文档树进行编码的算法如下：

算法：Coding_method(T，code)

输入：XML文档的根节点T，1

输出：文档中每个节点元素的编码code

Begin

Printf(code); //输出当前节点编码code

ChildNumber=ChildNumber of T; //先计算节点的孩子个数

temp=log2ChildNumber;

if(temp!=|temt|) high=temp+1; //high表示要下移的层数

else high=temp;

code=code*(2^high); //下移high层时编码左移high位，即末位加high个0

for(i=1; i<=ChildNumber) //对每个子节点分别进行编码

{ Temp2=child[i] of T

Coding_method(Temp2,code); //对子节点递归编码

code++; //编码值加1

}

End

BTB编码可以有效地支持文档更新，当插入新节点时，仅需要对插入位置节点的子孙节点重新编码，其余节点编码不变。例如，要在s2节点下面增加一个孩子节点，只需要修改s2节点2个子节点的编码，其它编码不变。

1.3 BTB编码的性质

性质1：每个节点BTB编码的二进制长度等于节点在文档二叉树中的层次。

证明：当层次length=1时，为根节点，编码是1，1的二进制长度为1；设length=k时，编码L(k)的二进制长度为k；则length=k+1时，编码L(k+1)=L(k) ×2+0或L(k+1)=L(k) ×2+1，因为L(k)的二进制长度为k，故L(k+1)的二进制长度为k+1。证毕。

性质2：给定一个节点u的编码lu，它的任一祖先节点编码都是lu所表示的二进制串的前子串。

证明：由BTB编码原理可知，除根节点外，任一节点编码都是由其双亲节点编码变化得来，即在双亲节点编码后补一位，0/1，故，它的任一祖先节点的编码都是其编码的前子串。证毕。

性质3：给定一个节点u的编码lu，它在文档二叉树中h层的祖先节点的编码可由下式求出

L(parent)=lu/2k-h

其中，k=|log2lu|+1，k计算的是lu的二进制位数。

证明：由性质1可知，h层节点的二进制编码长度为h；由性质2可知，节点u在h层的祖先节点的编码为lu所表示的二进制串的前子串。所以，u在h层的祖先节点的编码是lu所表示的二进制串的前h位子串，故原式成立。证毕。

给定u和v 2个节点，设它们在文档二叉树中的层数分别为n1和n2。u是v的祖先节点，当且仅当节点u的编码等于节点v编码的前n1位。u是v的父亲节点，当且仅当u的编码与v的编码的前n1位完全相同，且n2=n1+1。

1.4 对文档更新的支持

设节点u的编码为lu，孩子数为n。在节点u处插入子节点v时，对新节点编码的处理有以下3种情况：

（1）当n=0时，即u为叶子节点，新节点v作为节点u的孩子节点插入到文档二叉树中，对新节点v编码，编码为：lu×2。其它节点编码不变；

（2）当n=1时，节点u只有一个孩子节点，若新节点作为节点u的右孩子插入到文档二叉树中，编码为：lu×2+1。其它节点编码不变；

（3）当n=1时，节点u只有一个孩子节点，若新节点作为节点u的左孩子插入到文档二叉树中，节点u原来的孩子节点重新编码为：lu×2+1，节点v编码为lu×2。其它节点编码不变；

（4）当n=2时，文档二叉树中没有空位置插入新节点，调用算法Coding_method(u，lu)对节点u的子树进行重新编码，其它节点编码不变；

（5）对于删除节点的处理是，直接把该节点的编码删除，其它节点编码不变。

2 实验及分析

目前的编码方案都存在一定缺陷，区域编码不能很好地支持文档更新，前缀编码支持文档更新，但需要占用大量的存储空间。本文提出的BTB编码，采用的是二进制编码形式，存储时以十进制存储，节省大量空间，并且对于文档的更新，更新时只需要修改少量数据。

实验是在一台操作系统为Windows XP、处理器为2.16 GHz、内存为2 Gbit的PC机上进行的，算法使用Java编码实现，所采用的XML测试数据是来源于一个针对XML的基准测试项目X-Mark[7]数据集，实验选择典型的区域编码XISS[3]及前缀编码LSDX[5]进行比较，实验结果如图3。

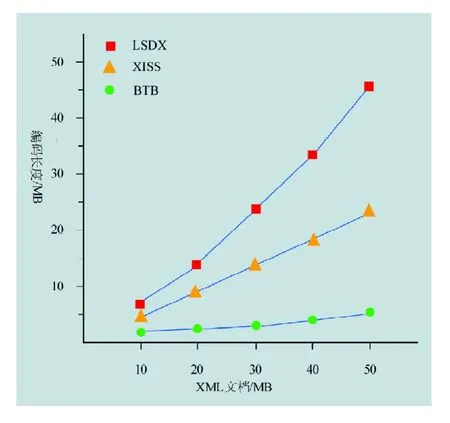
图3 编码长度比较

实验结果表明，对于相同大小的XML文档，由于BTB编码采用的是二进制编码，占用的存储空间最小；LSDX编码用字母表示节点的位置关系，占用的存储空间最大。

3 结束语

本文提出了BTB编码方案，该方案可以有效地支持祖先/后代关系、父子节点关系和兄弟关系的判断，并且判断可在常数时间完成。对于存储，该编码由于采用了二进制的编码方式，每个节点具有唯一编码，以十进制数据存储，占用较少的存储空间。在该编码下的结构连接算法是下一步的研究方向。

[1] Zhang C, et al. On Supporting Containment Queries in Relational Database Management Systems[C] . Proc. of SIGMOD, 2001:425-436.

[2] Michael Erdmann, Rudi Studer. How to structure and access XML documents with ontologies[J] . Data & Knowledge Engineering, 2001(36): 317-335.

[3] Cohen E, Kaplan H, Milo T. Labeling Dynamic XML Trees[C] .Proc. of PODS, 2002: 271-281.

[4] Duong M, Zhang Y. A New Labeling Scheme for Dynamically Updating XML Data[C] . Proc. of ADC, 2005.

[5] Wang W, Jiang HF, Lu HJ, Jeffrey XY. PBiTree coding and efficient processing of containment joins[C] . Dayal U, Ramamritham K, Vijayaraman TM, eds. Proc. of the 19th Int'l Conf.on Data Engineering. Los Alamitos: IEEE Press, 2003: 391-402.

[6] 文华南，刘先锋，李文锋，李玲勇. 高效查询的XML编码方案[J] . 计算机应用， 2010， 30（3）： 831-834.

[7] SCHMIDT A, WAAS F, KERSTEN M, et at. XMark A benchmark for XML data management[C] . Proc. of the 28th VLDB Conf. HongKong VLDB Endowment, 2002: 974-985.