基于偏度-峰度检验的无线局域网室内定位算法

宋震龙，蒋刚毅，黄晁，郁梅，张家乐

（1.宁波大学 信息科学与工程学院，浙江 宁波 315211；2.中国科学院 计算技术研究所，北京 100080；3.宁波中科集成电路设计中心，浙江 宁波 315040）

1 引言

随着物联网和智慧城市建设的兴起和快速发展，基于位置的服务应用越来越广泛。传统的GPS和蜂窝网定位技术在室外能达到较高的定位精度，但在室内环境下，由于射频信号受到阻隔而无法有效定位。学者们提出了许多针对室内定位的定位技术，其中 WLAN定位技术可以充分利用已经普遍存在的无线局域网资源，不需要部署其他硬件设施，具有低成本优势。因此基于 WLAN的室内定位技术越来越受到关注[1～3]。

目前 WLAN室内定位方法中应用最普遍的是位置指纹定位法[4～6]，该方法分为离线训练和在线定位2个阶段。离线训练阶段在待定位区域选定一系列参考位置点，在这些参考位置点处采集来自不同无线接入点(AP, access point)的RSS值，将参考位置点坐标和采集的RSS数据存储在数据库中，组成射电地图(RM, radio map)。在线定位阶段通过匹配算法比较实时采集的 RSS信息和射电地图中的信息，估计用户的位置。

室内环境下射频信号传播非常复杂，墙壁、门窗和桌椅等基础设施以及人员走动的影响导致射频信号传播产生显著的多径现象和阴影效应，因此室内固定位置处 RSS信号的时变性很强[7,8]。Kaemarungsi统计了室内WLAN环境下RSS样本的总体分布情况[9]，共选取了299个RSS样本，每个样本中含有2 962～3 956个RSS信号值，统计结果表明，有214个样本（约占总样本数的71.6%）的总体分布服从正态分布，其余样本的总体分布则表现为严重左偏、严重右偏、多峰或其他非正态分布。RSS样本总体分布不一致，使室内定位产生较大的定位误差[9～11]。Yousief等人提出了一种直方图室内定位算法[12]，但是RSS样本直方图不平滑，经常出现一些零值，定位精度不高。Kushki等人提出了一种基于核函数的定位方法[13]，在RSS样本总体分布未知的情况下，利用核函数估计总体的概率密度，但有限的 RSS样本数据无法准确估计样本总体的分布。Ma等人提出用多项式函数拟合RSS样本的概率直方图分布[14]，但这种方法有时会出现函数不收敛的情况，无法准确拟合出样本总体的分布函数。为了准确估计所有RSS样本总体的概率密度，本文提出了一种基于偏度-峰度检验的室内定位算法：离线训练阶段根据偏度-峰度检验法检验 RSS样本是否来自正态总体，对于接受和拒绝零假设的样本分别利用正态分布和核函数估计其总体的概率密度，在线定位阶段利用贝叶斯匹配法估计位置。实验结果表明，本文算法比传统算法有更高的定位精度，平均定位误差减小15%以上，而且在达到相同定位精度的情况下离线阶段训练样本数比传统算法少，能明显降低离线阶段的工作量。

2 基于偏度-峰度检验的室内定位算法

2.1 偏度与峰度

检验一个样本是否服从正态分布的方法有很多，包括 Kolmogorov检验、χ2拟合优度检验、Shapiro-Will检验和偏度-峰度检验等[15]。Kolmogorov检验是一种较准确的检验方法，但Kolmogorov检验只有当假设的分布完全已知的时候才适用，假设的分布不包含需要从样本里估计的未知参数。χ2拟合优度检验比较灵活，允许分布中包含待估的未知参数，但χ2检验要求数据分组，且χ2检验犯第二类错误（接受了不正确零假设的错误）的概率往往较大。Shapiro-Will检验法能有效地检验样本正态性，但Shapiro-Will检验要求样本容量不大于50。偏度-峰度检验法通过计算样本偏度和峰度检验样本总体是否服从正态分布，是一种快速、有效的正态性检验方法，且对样本容量没有严格要求。因此本文选用偏度-峰度检验法检验 RSS样本是否来自正态总体。

偏度和峰度分别是描述总体中所有取值分布形态对称性和陡缓程度的统计量。随机变量X的偏度和峰度是指X的标准化变量阶矩和四阶矩[15]：

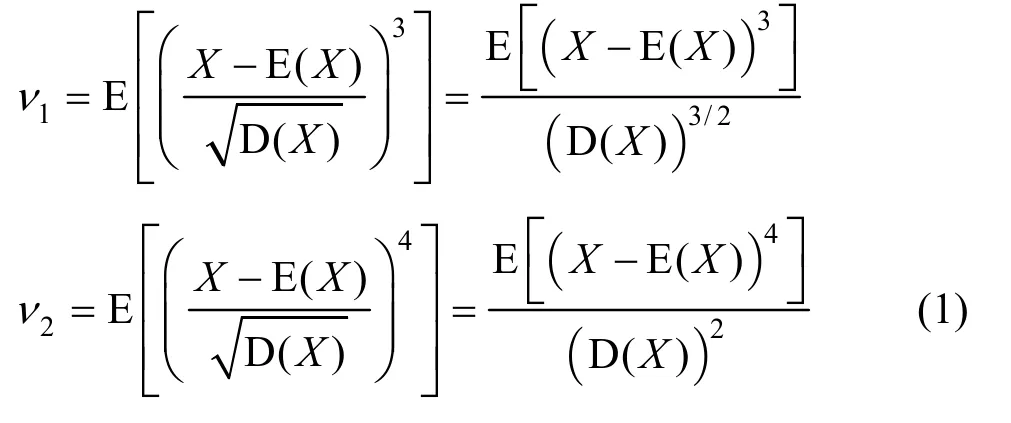
其中，E(X)和D(X)分别为随机变量的期望和方差。当随机变量X服从正态分布时，偏度ν1=0且峰度ν2=3。

2.2 提出假设

设X1,X2,…,Xn是来自RSS总体X的样本，则ν1和ν2的矩估计量分别为

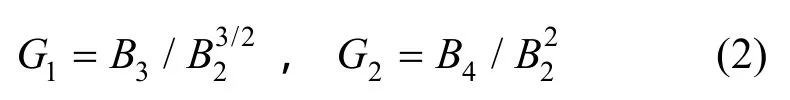
其中，Bk(k=2,3,4)是样本k阶中心矩，G1，G2分别为样本偏度和样本峰度。

若总体X为正态变量，则有

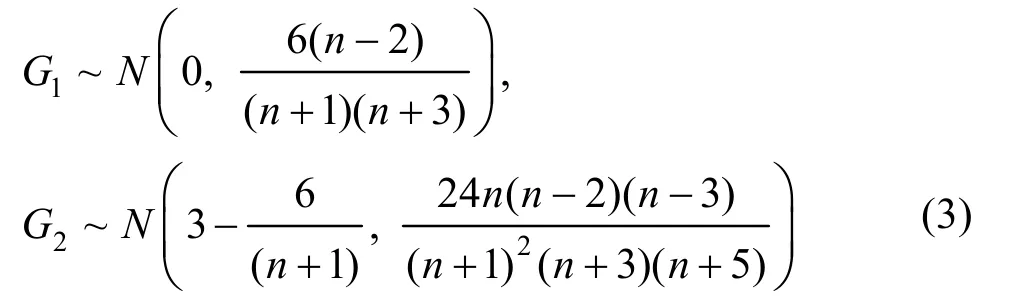
提出假设：

其中，H0和H1分别为零假设和备则假设。

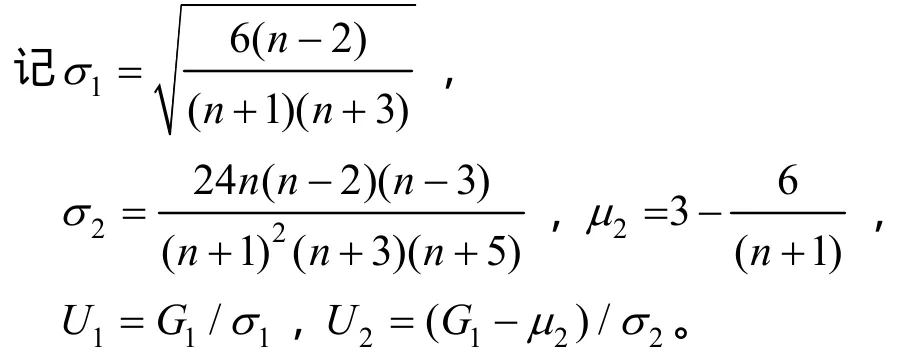
当H0为真且n充分大时，有

取显著性水平为α(0＜α＜1)，则H0的拒绝域为

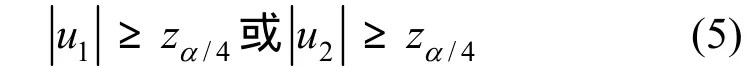
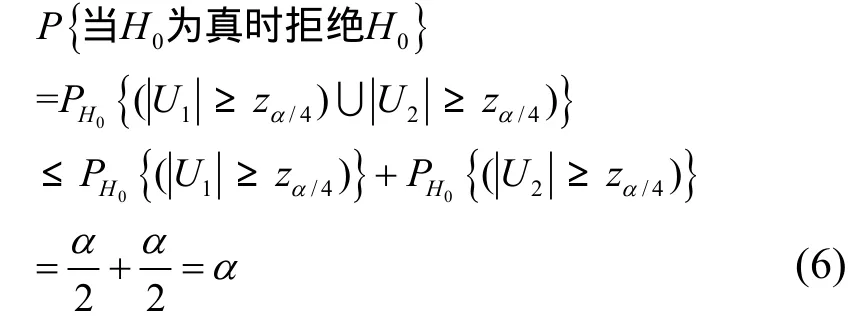
2.3 正态估计

将离线阶段采集的 RSS样本按式(5)检验|u1|和|u2|是否满足H0的拒绝域，如果不满足则接受H0，认为该样本的总体在显著水平为α(0＜α＜1)时服从正态分布，此样本的概率密度函数近似为

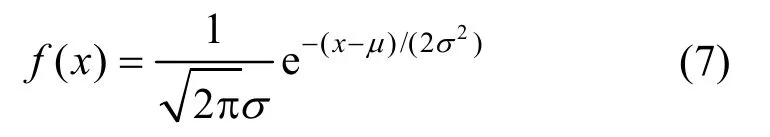
其中，μ和σ为正态分布的参数。使用最大似然估计法可以估计正态分布的参数，即

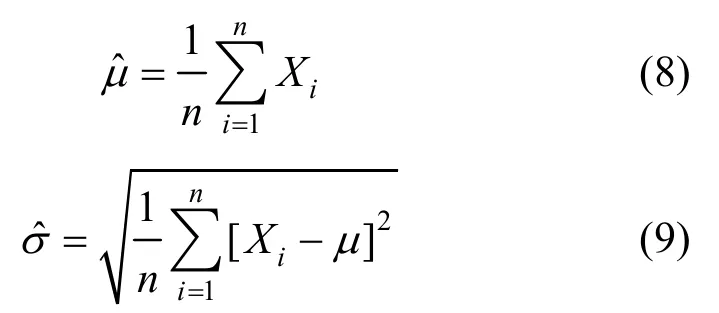
2.4 核函数估计

如果离线阶段采集的RSS样本按式(5)检验|u1|和|u2|满足H0的拒绝域，则认为这些样本的总体分布在显著水平为α时与正态分布有较大差异。本文中用核函数方法估计这些样本的总体分布。核估计方法是一种在总体分布未知的情况下估计总体概率密度的方法[16]。

定义设总体X具有概率密度f(x)，f(x)未知，X1,X2,…,Xn为取自总体X的一个样本，存在全直线上一有界函数k(y)≥ 0 ，满足

满足上述定义的核函数有很多，其中指数核函数对样本的概率密度估计效果较好[11]，因此本文选用指数核函数：

拒绝H0的样本利用指数核函数估计其总体的概率密度函数：

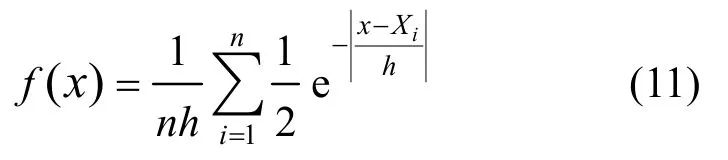
2.5 贝叶斯匹配

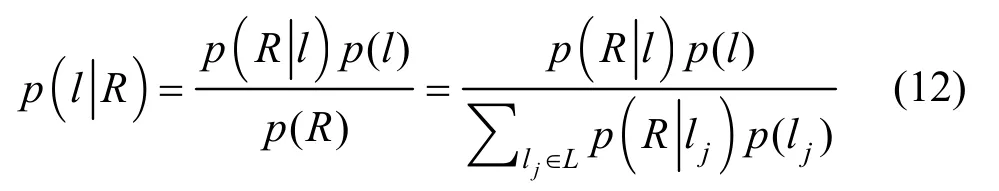
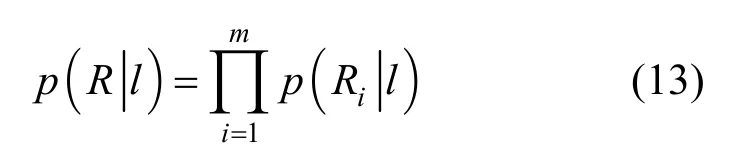
其中，m表示 AP的数目，表示在参考位置l处采集的来自第i个 AP的 RSS样本的似然函数，按式(7)或式(11)计算。

p表示参考位置l与在线阶段真实位置的接近程度，通过式(14)估计用户位置：

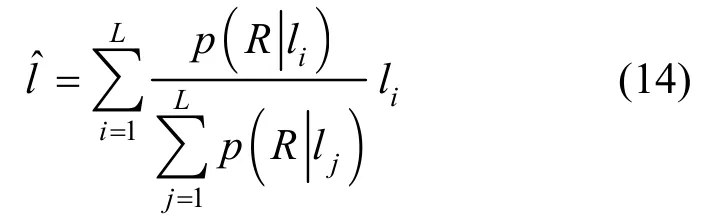
2.6 定位算法步骤

基于偏度-峰度检验的室内定位算法的主要步骤如下，其中，step1～step4为离线训练阶段，step5～step6为在线实时定位阶段。

step1 在定位区域选定参考位置点，在每个参考位置点处采集来自不同 AP的一定数量的 RSS值，组成RSS样本。

step2 设定显著性水平α和指数核函数宽度h。

step3 按式(5)检验RSS样本是否接受H0。

step4 如果接受H0，则认为该样本来自正态总体，根据式(8)和式(9)计算正态分布参数的估计值并存入数据库，否则将RSS样本原始值存入数据库。

step5 实时采集 RSS值，并根据数据库中存储的数据按式(7)或式(11)计算参考位置l的来自第i个AP的RSS样本的似然函数，并按式(13)计算参考位置l的似然函数。

step6 按式(14)估计用户的位置。

基于偏度-峰度检验的室内定位算法的流程如图1所示。

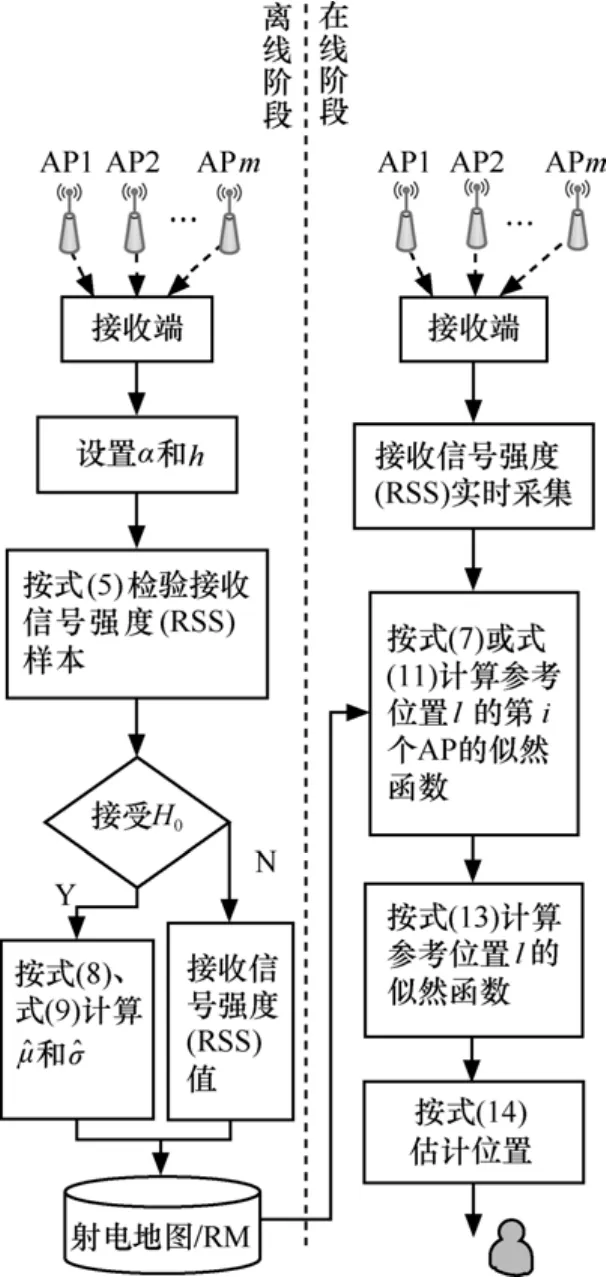
图1 基于偏度-峰度检验的室内定位算法流程

3 实验结果与分析

实验环境为如图2所示的典型的WLAN室内定位场景，面积为37.2m×18m。此区域有4个型号为NETGEAR WG602的AP，分别位于606室、607室、610室和613室。RSS采集装置选用惠普dv2305TX笔记本电脑，无线网卡型号为 Intel PRO/wireless 3945ABG，操作系统为 Windows 7。参考位置点主要在走廊、电梯口、610室和613室选取，每个参考位置点间隔2m，共有64个，利用笔者开发的RSS采集软件在每个位置点采集RSS样本，采集速率为2sample/s。本文用于定位的AP数目为4个，总的训练RSS样本数目为64×4=256个。

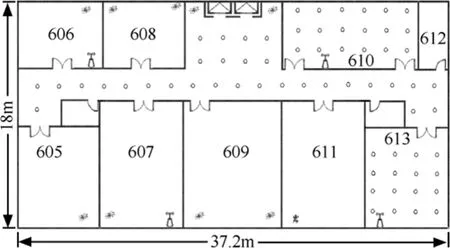
图2 WLAN室内定位环境(圆圈代表参考参考位置点，代表此区域存在的AP)

定位误差的评判标准为估计位置点ˆl和真实位置点坐标l之间的欧式距离，即

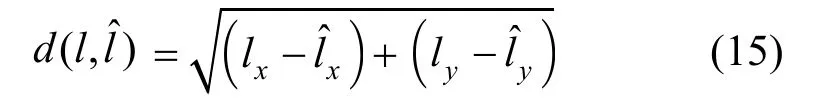
3.1 显著性水平和核宽度分析

显著性水平α表示当H0为真时拒绝H0的概率。表1给出了显著性水平α与接受H0的样本数的关系，其中，总的RSS训练样本为256个，每个RSS样本的样本容量为60。从表1中可以看出α较小时，接受H0的样本数占总样本数的80%以上，α较大时，接受H0的样本数占总样本数的比例不足20%。这2种情况下都有较多的样本导致了误判，影响定位精度。

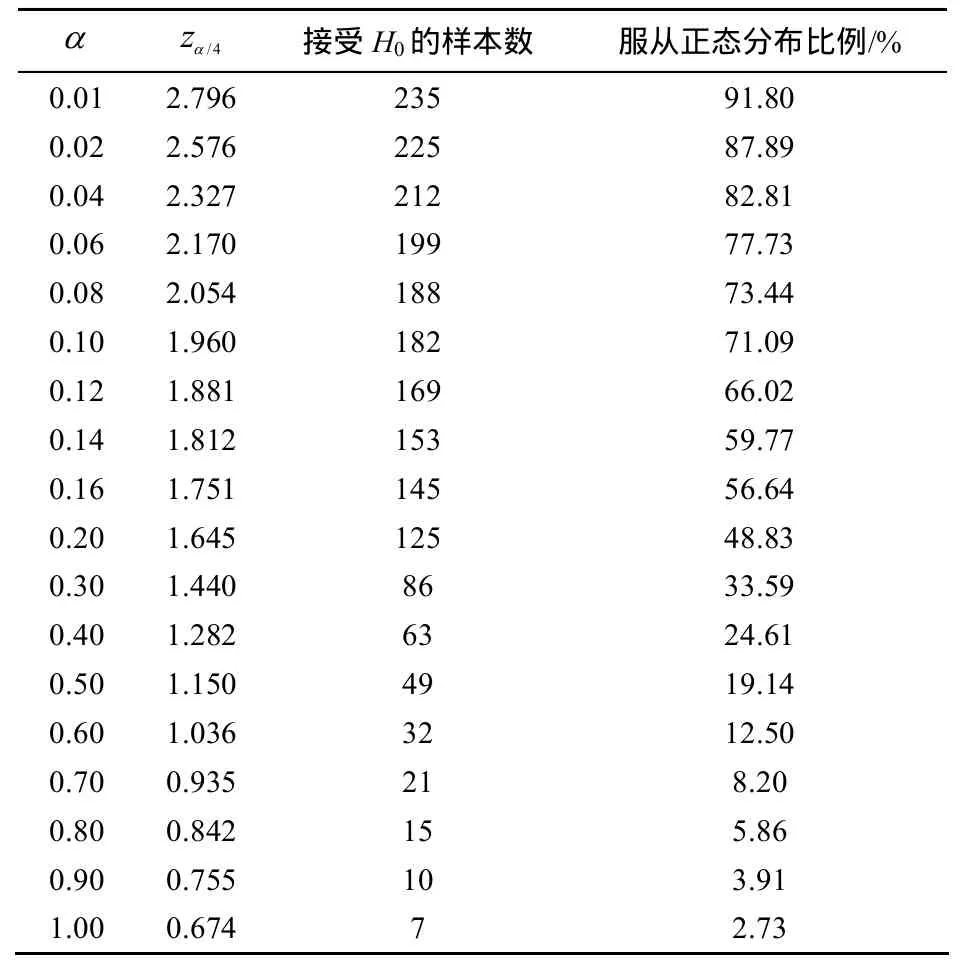
表1 显著性水平α与接受H0的样本数

图3给出了显著性水平α取不同值时对平均定位误差的影响。从图中可以看出，α取0.1时平均定位误差最小，此时大约有71.09%的样本近似为正态分布。从图中还可以看出当α小于0.06时，平均定位误差的变化趋势比较陡峭，这是由于有较多的不服从正态分布的样本如严重左偏、严重右偏或多峰的样本被误判为了正态分布。当α大于0.4时，平均定位误差的变化趋势比较缓慢，这是由于α大于0.4时接受H0的样本的偏度和峰度都比较小，此时指数核函数估计的概率密度与正态分布很接近。

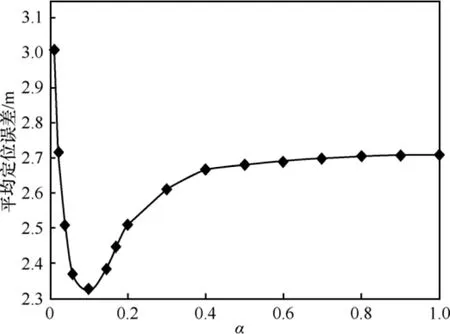
图3α取不同值时对平均定位误差的影响

核宽度h是核函数的平滑参数。图4所示为当α=0.1，RSS样本的容量为60时，核宽度h与平均定位误差之间的关系。从图中可以看出，核宽度h取值太大或太小都有较大的定位误差。这是因为若h取得太小，随机干扰增大，估计结果会失去准确性；若h过大，估计曲线太平坦，以至于无法表征样本分布的变化情况。可以看出h取 2.2时平均定位误差最小。

图4 核宽度h取不同值时的平均定位误差

3.2 与其他算法比较

比较了本文提出算法与现有的直方图方法[12]、多项式拟合方法[14]和核函数方法[13]等算法的定位性能。本文算法显著性水平α取0.1，核宽度h取2.2。

离线阶段样本容量决定了离线阶段的工作量，也决定了室内定位法的效率。如图5所示为提出的算法与现有的几种定位算法在不同的训练样本容量下的定位精度，训练样本容量选择[10,120]区间内的 12组数据。从图中可以看出随着训练样本容量的增加，4种算法的平均定位误差都逐渐减小，当样本容量大于100时定位误差趋于稳定，这说明不能通过无限地增大样本容量使定位精度无限提高。其原因是当样本容量较小时无法准确表征复杂室内环境下的位置信息，但当样本容量增大到一定程度时RSS样本所含的位置信息基本保持不变。从图中还可以看出基于偏度-峰度的定位算法在相同的样本容量下具有最小的平均定位误差，这是由于该算法能够在有限的样本容量下更准确地估计所有样本的总体分布，使似然函数更加准确，从而按式(14)估计的位置更精确。而且，基于偏度-峰度的定位算法只需要较少的训练样本容量就能到达其他算法同样的定位精度。例如，要达到小于 2.6m的平均定位误差，基于偏度-峰度的定位算法只需要在离线阶段采集30个RSS值，而核函数算法则至少需要 80个。这表明在相同的定位精度下，本文算法能够有效减少离线阶段的数据采集时间，节省人力成本投入。

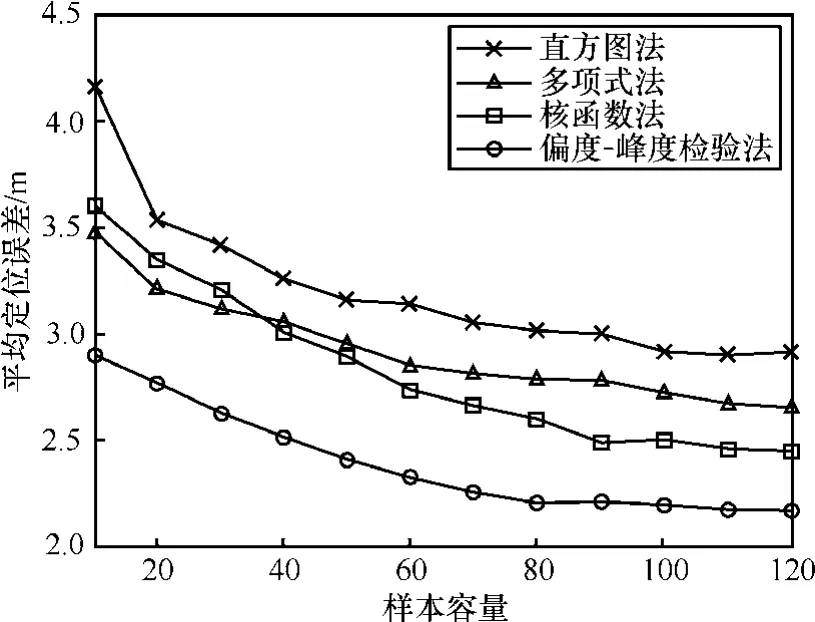
图5 不同训练样本容量下的平均定位误差

图6给出了当RSS训练样本容量为60的条件下几种定位算法的定位误差的累积概率分布。可见，使用基于偏度-峰度的定位算法误差在2m以内的概率为 63.3%，高于其他算法的 57.1%、52.5%和46.4%。表2给出了当RSS训练样本容量为60的条件下不同算法的定位误差比较。可以看出，基于偏度-峰度的定位算法的平均定位误差比核函数方法、多项式拟合方法和直方图方法分别减少0.41m(15.0%)，0.54m(18.9%)和0.85m (26.8%)，而且基于偏度-峰度的定位算法具有更小的误差标准差。这表明该算法在有效提高定位精度的同时还具有较好的稳定性。原因是在复杂的室内环境下，基于偏度-峰度的定位算法准确地估计了所有RSS样本总体的概率密度，使似然函数计算更准确，从而能更精确地估计位置。

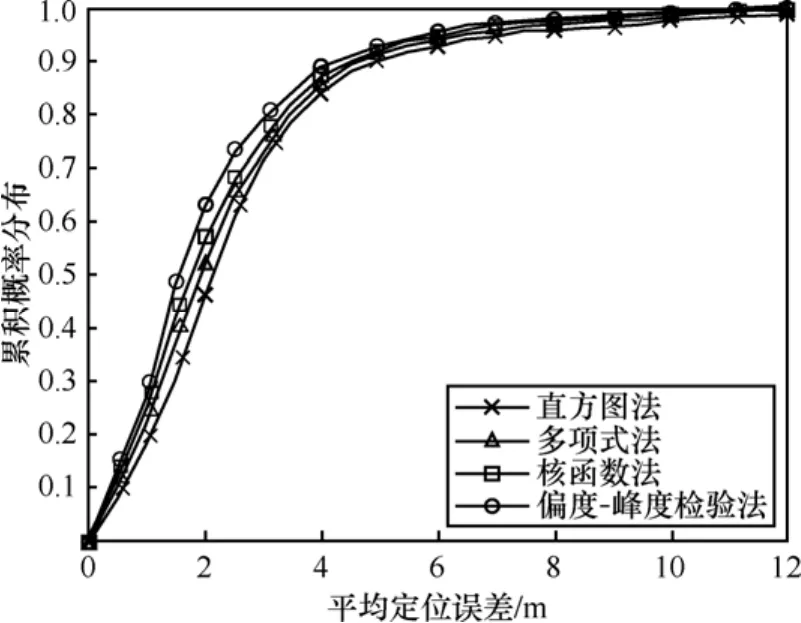
图6 不同算法定位误差的累积概率分布

表2 不同算法的平均定位误差比较/m

4 结束语

在无线局域网室内环境下，RSS样本的总体分布呈现不一致的现象，如何准确估计样本总体的分布是提高定位精度的关键。本文提出了一种基于偏度-峰度检验的室内定位算法，接受和拒绝零假设的样本分别利用正态分布和核函数估计其总体的概率密度，可准确估计所有 RSS样本总体的概率密度，使位置估计更加精确。实验结果表明提出算法的定位精度比传统方法提高15%以上，且在相同定位精度下，需要更少的训练样本容量，大大减小了离线阶段的工作量。提出的算法不仅适合于WLAN室内定位技术，而且适合其他基于RSS的室内无线定位技术，如RFID定位技术和蓝牙定位技术等。需要说明的是，本文算法在线定位阶段没有考虑当前定位状态与下一定位状态之间的相关性，因此不适合运动速度较快的目标定位。下一步研究中，针对快速运动目标跟踪定位问题，须考虑定位状态之间的相关性，提高动态跟踪定位精度。

[1] VERA R, OCHOA S F, ALDUNATE R G. EDIPS: an easy to deploy indoor positioning system to support loosely coupled mobile work[J].Personal and Ubiquitous Computing, 2011, 15(4): 365-376.

[2] 林以明, 罗海勇, 李锦涛等. 基于动态 radio map的粒子滤波室内无线定位算法[J]. 计算机研究与发展, 2011, 48(1): 139-146.LIN Y M, LUO H Y, LI J T, et al. Dynamic radio map based particle filter for indoor wireless localization[J]. Journal of Computer Research and Development, 2011, 48(1): 139-146.

[3] GU Y Y, LO A, NIEMEGEERS I. A survey of indoor positioning systems for wireless personal networks[J]. IEEE Communications Surveys & Tutorials, 2009, 11(1): 13-32.

[4] KUSHKI A, PLATANIOTIS K N, VENETSANOPOULOS A N.Intelligent dynamic radio tracking in indoor wireless local area networks[J]. IEEE Transactions on Mobile Computing, 2010, 9(3):405-419.

[5] FANG S H, LIN T N. A dynamic system approach for radio location fingerprinting in wireless local area networks[J]. IEEE Transactions on Communications, 2010, 58(4): 1020-1026.

[6] 徐玉滨, 邓志安, 马琳. 基于核直接判别分析和支持向量回归的WLAN室内定位算法[J]. 电子与信息学报, 2011, 33(4): 896-901.XU Y B, DENG Z A, MA L. WLAN indoor positioning algorithm based on KDDA and SVR[J]. Journal of Electronics & Information Technology, 2011, 33(4): 896-901.

[7] FANG S H, LIN T N, LEE K C. A novel algorithm for multipath fingerprinting in indoor WLAN environments[J]. IEEE Transactions on Wireless Communications, 2008, 7(9): 3579-3588.

[8] MAZUELAS S, BAHILLO A, LORENZO R M, et al. Robust indoor positioning provided by real-time RSSI values in unmodif i ed WLAN networks[J]. IEEE Journal of Selected Topics in Signal Processing,2009, 3(5): 821-830.

[9] KAEMARUNGSI K. Design of Indoor Positioning Systems Based on Location Fingerprinting Technique[D]. Pittsburgh, USA: University of Pittsburgh, 2005.

[11] HONKAVIRTA V, PERALA T, LOYTTY S A, et al. A comparative survey of WLAN location fingerprinting methods[A]. Proceedings of the 6th Workshop on Positioning, Navigation and Communication[C].Hannover, 2009. 243-251.

[12] YOUSIEF M, AGRAWALA A. The Horus WLAN location determination system[A]. The 3rd International Conference on Mobile Systems Applications, and Services[C]. New York, 2005. 205-218.

[13] KUSHKI A, PLATANIOTIS K, VENETSANOPOULOS A. Kernel-based positioning in wireless local area networks[J]. IEEE Transactions on Mobile Computing, 2007, 6(6): 689-705.

[14] MA L, XU Y B, ZHOU M. Accuracy enhancement for fingerprint-based WLAN indoor probability positioning algorithm[A]. The 1st International Conference on Pervasive Computing, Signal Processing and Applications[C]. Harbin, China, 2010. 167-170.

[15] KVAM P H, VIDAKOVIC B. Nonparametric Statistics with Applications to Science and Engineering[M]. Hoboken: John Wiley & Sons,2007.

[16] 李裕奇, 赵联文, 王沁等. 非参数统计方法[M]. 成都: 西南交通大学出版社, 2010.LI Y Q, ZHAO L W, WANG Q, et al. Nonparametric Statistics Methods[M]. Chengdu: Southwest Jiaotong University Press, 2010.