无线传感器网络高可靠低维护地理路由协议

方效林，高宏，熊蜀光

(哈尔滨工业大学 计算机科学与技术学院，黑龙江 哈尔滨 150001)

1 引言

无线传感器网络(WSN, wireless sensor networks)[1,2]通过大量部署在监测区域内的传感器节点，采集网络覆盖区域内感知对象的信息，并通过多跳的无线通信方式，将收集处理后的信息提供给终端用户。在无线传感器网络中，地理路由协议使得数据分组可以通过多跳无线传输到达指定地理位置附近的节点，因而具备广泛应用[3～5]。

地理路由算法一般都假设每个节点已知邻居节点的坐标信息，源节点已知目的节点的坐标信息。坐标信息的获取可以通过定位算法来实现。在地理路由过程中，节点选择距离目的节点最近的邻居节点进行转发数据分组的方式被称为贪婪转发模式。贪婪转发模式由于其原理简单，计算复杂度很低，并且生成的路径接近最优化路径等特点，成为地理路由算法中最常用的转发策略。但在实际的传感器网络中，由于网络部署不均匀或者部分传感器节点因故障或者能量耗尽而失效，会导致网络形成“空洞”。节点用贪婪路由算法转发数据分组遇到空洞时，由于找不到比自身更接近目的节点的邻居节点，因而数据分组无法继续转发，贪婪路由失败。贪婪路由失败时，就需要一种方法将数据分组绕过空洞传输到目的节点。

数据分组以沿着空洞边缘绕过空洞的转发方式，称为周边转发模式。现有的地理路由算法通常具有贪婪转发和周边转发2种模式，不同路由算法只是采用不同的模式切换机制。贪婪转发是基本的转发模式，当贪婪转发遇到路由空洞而失败时，路由算法就转入周边转发模式，直到能够恢复贪婪转发模式时又进入贪婪转发模式。贪婪转发和周边转发2种模式相互运用能够有效地绕过路由空洞，保证数据的可靠传输。

虽然基于贪婪转发和周边转发2种模式的地理路由算法需要维护的路由表小，路由效率高，但是它们都共同面临网络平面化问题。网络平面化需要将网络在周边转发模式之前进行平面化处理，即将网络通过平面化算法，形成以节点为顶点、链路为边，并且不存在交叉边的图。以前有关于地理路由算法的论文[4]，但是基于UDG图。UDG图是理想的节点通信方式，适用于理想环境下的理论分析，但在真实的网络环境中并不可行[5]。

本文提出一种具有高可靠性和低维护成本的地理路由协议RPR，其基本思想是将网络划分为规则多边形区域，并在贪心路由失败时将多边形区域内的所有节点看作一个虚拟节点进行周边路由。多边形区域间通信能够降低平均路由路径长度，从而提高了路由的可靠性。基于区域划分的网络平面化策略不需要检测和删除相交链路，因此减少了路由维护开销。

与现有平面化方法相比，基于地理位置划分的平面化方法有以下优势：①网络平面化方法简单有效；②可以实现多边形间可靠路由算法；③能够减少路由路径长度。

将地理位置划分为规则多边形区域可以有多种方法，如将网络划分为规则正方形、等边三角形、正六边形等。每种划分方法都有各自的优缺点，可以根据不同的应用选用不同的划分方式。在二维平面划分方法中，正六边形划分方法能够最好地保留网络的连通性，从而提高路由的可靠性，本文于是选择正六边形的划分方法进行网络平面化处理。

本文的主要贡献如下。

1) 使用区域划分的方法进行网络平面化处理。将网络在地理上划分为规则六边形区域，该平面化处理方法简单有效，能降低平面化处理的通信开销。

2) 提出基于区域划分的地理路由协议RPR仍具有贪婪转发和周边转发2种模式。在贪心路由失败时，将多边形区域当作一个整体进行周边路由。此方法能够减小平均路由路径长度，从而降低路由开销，提高路由的可靠性。

3) 分析了区域内不连通情况。划分的六边形区域内节点组成的图可能不连通，本文给出不连通情况下的路由方法，并分析了区域内不连通概率。

4) 对提出的平面化方法和地理路由策略与现有的方法作了对比实验。实验结果显示本文方法具有维护代价低，路由可靠性高等优点。

2 相关工作

目前已有很多关于地理路由算法的工作，其基本过程一致，都是在贪心模式失败时转入周边模式。假设数据分组的目的节点为t，路由算法在节点s贪心转发失败进入周边转发模式，以下是各种平面地理路由算法周边转发模式的转发算法。GFG(greedy-face-greedy)算法[6]绕平面寻找与连线st相交的边，以它们的交点p临近目的节点的方式逐步向目的节点靠近。GFG算法绕平面的方向与进入的面与平面图的内表面和外表面有关，进入内表面时算法按逆时针方向绕平面转发数据分组，进入外表面时方向正好相反。Compass Routing II算法[7]与GFG类似，不同的是Compass Routing II绕平面一周，找出与st相交并且距离目的节点最近的交点p，算法将数据分组转发到交点p所在的另一个面。GPSR(greedy perimeter stateless routing)算法[3]按右手定则绕平面寻找一个顶点u，它与下一个顶点v组成的边uv与st相交，算法从节点u开始进入下一个平面继续路由。GPSR算法与GFG算法的不同之处在于，GPSR总是试图进入离目的节点更近的另一个平面，而GFG进入的平面有可能没有改变。GOAFR+(greedy other adaptive face routing)算法[8]绕平面一周，找出离目的节点最近的节点，从这个节点开始进入下一个平面。为区分GOAFR+，文献[4]中将 greedy other adaptive face routing[9]命名为GOAFR++。GOAFR++算法绕平面一周，找出平面上距离目的节点最近的点p(点p可以是某条边上的一点)，并从点p所在边的2个顶点其中一个进入下一个平面。GPVFR(greedy path vector face routing)算法[10]绕平面寻找顶点u，它与下一个顶点v组成的边uv与st相交，算法从节点u开始进入下一个平面继续路由，但是不再保存st，而以ut作为判断与面相交的直线。文献[4]对上面同种路由算法作了总结。

以上所有算法都需要预先将网络进行平面化处理。将网络进行平面化处理算法有 GG[11]、RNG[12]和LDT[13]，这3个算法都是基于UDG(unit-disk graph)或伪UDG图的。在UDG图中，任意2节点间有边当且仅当它们之间的欧几里德距离小于等于一个固定的发射半径，这个发射半径可以认为是节点的无线发射半径。伪UDG图是UDG图的扩展，它的发射半径不是固定值，而是夹在一个最大值和一个最小值之间的数。在GG图中，任意2个顶点u和v间有边当且仅当以(u,v)为直径的圆内不包含其他顶点。在RNG图中，任意2个顶点u和v间有边，当且仅当以u为圆心以(u,v)为半径的圆和以v为圆心以(u，v)为半径的圆的相交部分不包含其他顶点。局部Delaunay三角剖分(LDT)算法中，假设T为顶点集V的任意三角剖分，则T是V的一个Delaunay三角剖分，当且仅当T中的每个三角形的外接圆的内部不包含V中任何的点。以上平面化算法在基于UDG图的网络中能够很好地进行平面化处理，但是在真实的传感器网络环境中这些算法不实用。

为了让平面地理路由算法能够适用于真实的传感器网络应用，Y.J.Kim等人提出了CLDP平面化算法[5]。CLDP算法是目前提出的唯一适用于不满足 UDG图条件的传感器网络平面化地理路由算法。该算法对网络中的每条链路都发送探测分组，等待探测分组返回之后，在确定删除某些边后不影响网络连通性时才将该边删除，从而达到平面化。CLDP算法能够保证周边转发机制在实际复杂的传感器网络中正确地运行，但是每个节点都要发探测包以确定删除一些边，开销相当大。平均每个节点在网络生存时间里大约需要发送几百到上千个数据分组来进行和维持平面化过程。LCR算法[14]针对CLDP算法在网络初始化阶段对网络的结构进行平面化而导致开销较大的缺陷得到改进。LCR算法在初始化时节点并不进行平面化处理，而是在数据分组路由过程中遇到路由回路时，才进行局部CLDP平面化。在局部CLDP平面化处理结束后继续转发数据分组。LCR算法不仅能在非 UDG网络中保证数据的可靠传输，并且LCR在平面化处理中的开销比CLDP算法降低2个数量级。

3 区域划分的平面化方法

文献[15]假设传感器节点的发射半径是一个固定值，分析了三角形、正方形和六边形3种网络拓扑的优劣，并得出三边形拓扑可靠性最高的结论。如图1所示，三角形网络拓扑每个节点规则地与6个节点相连，正方形拓扑与4个节点相连，六边形拓扑与3个节点相连。其中，三角形网络的可靠性最好，六边形网络的连通覆盖性最好，正方形网络的可靠性和网络连通覆盖性介于前2个之间，但是它的实现最简单。由于传感器网络具有不确定性，如何提高路由算法的成功率成为一个主要研究问题。本文选择可靠性最好的三角形网络拓扑设计路由算法，最大限度地保持网络的连通性和可靠性，提高路由算法的成功率。

图1 几种规则多边形网络拓扑

在真实的传感器网络中，规则多边形网络拓扑是不存在的。但是通过对地理位置进行划分，将每个小区域内的所有节点看成一个虚拟节点，小区域之间通信变成虚拟节点之间通信，这样得到的虚拟网络具有多边形网络拓扑的性质。本文通过以下步骤得到多边形网络拓扑：将整个网络平面进行正六边形区域划分，每个正六边形区域内的所有节点都被当作一个虚拟节点，虚拟节点的地理坐标为正六边形的中心，一个区域只与它的相邻区域进行通信。正六边形划分得到的虚拟网络拓扑实际上是三角形网络拓扑，如图2所示。

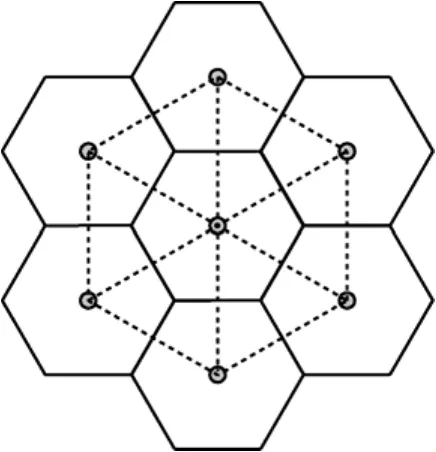
图2 虚拟三角形网络拓扑

给定一个网络，假设网络中每个节点都知道自身的地理位置信息，本文将地理位置进行正六边形区域划分。只要划分大小一致，每个节点都可以很容易计算出自身处于哪个六边形区域，如图3所示。很显然，按照图3的划分方式对地理位置进行划分得到的虚拟网络拓扑是一个平面图。为了叙述简便，下面给出区域划分的符号描述。

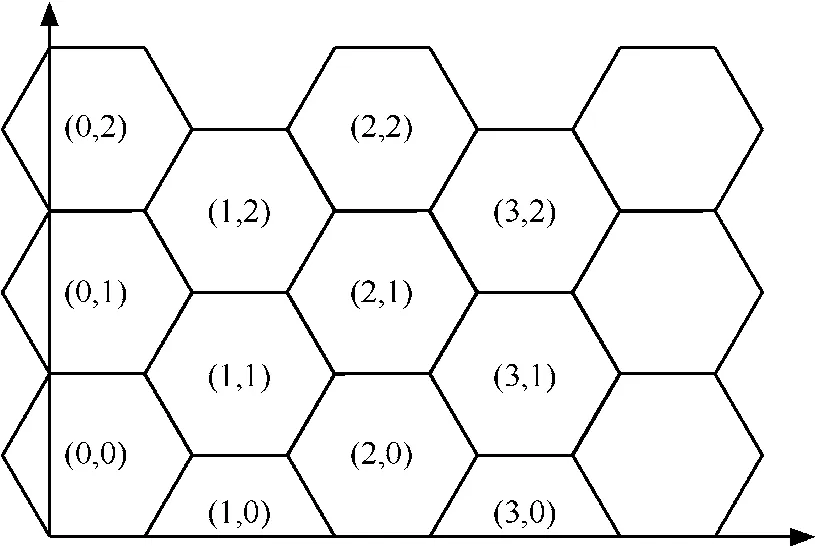
图3 正六边形地理位置划分

给定一个网络G=(V,E)，其中，V为网络中节点集合，E为网络中链路的集合。网络中每个节点都知道自身的地理位置坐标信息。

图3中，网络放置在一个二维平面R上，其中，R由许多正六边形区域组成，网络中每个节点属于一个六边形区域。每个小六边形区域表示为R(i,j)，其中，0 ≤i＜ ∞, 0≤j＜ ∞ ，六边形区域边长为L。区域R(i，j)的中心O(i,j)=(x,y)，其中，x=(1/2+3i/2)L。若i为偶数，则y=(1+2j)L；若i为奇数，则y=2jL。

定义1 对于给定网络G=(V,E)，区域R(i,j)是连通的，当且仅当以区域R(i,j)内的顶点组成的图G’=(V’,E’)是连通的，其中，V' ={v|v∈R(i,j)}，E' = {uv|u,v∈R(i,j),uv∈E}。

定义2 节点v所在的六边形区域为R(v)。

定义3 节点v在区域R(v)中的连通分量记为CP(v)，其中，CP(v)是以区域R(v)内的顶点组成的图G’=(V’,E’)的连通子图。

定义4 节点v所在六边形区域的中心为O(v)。

定义5 如果2个六边形区域R(i,j)和R(r,s)相连，则区域R(i,j)中至少存在一个节点u和区域R(r,s)中的某节点v之间有链路，即 ∃u∈R(i,j) ，∃v∈R(r,s)且uv∈E，记作R(i,j)∝R(r,s)。记区域R(i,j)的相连区域集合为C(i,j)。记节点u的相连区域集合为C(u)。

定义6 区域R(i,j)的相邻区域N(i,j)是围绕区域R(i,j)的6个六边形区域，即R(i,j)的相邻区域为N(i,j) = {R(i,j± 1 ),R(i± 1 ,j),R(i± 1 ,j+ 1 )}。

由定义5和定义6，显然相连区域与相邻区域是不同的概念，但是为了简化平面化过程，本文令六边形区域的路由相连区域RC(i,j) =C(i,j) ∩N(i,j)。这种设置是合理的，因为只要六边形的边长选取得足够长，跨区域的2个节点一般不能互相通信，这样就可以保证得到的虚拟图是一个平面图，并且不需要删除链路。

4 区域边长选择

六边形区域边长L的选取很重要，它会影响到平面化算法的好坏。由于传感器节点具有一定的通信范围，距离在通信范围内的节点间有可能互相通信，但是距离超过通信范围的节点间一般不能互相通信。如果选择边长L的值过小，二维平面R的划分太细，会导致有些小区域内可能没有传感器节点。而且L选取过小，还会导致有些不相邻的区域相连。此时为了得到路由相连区域，平面化过程会删除一些跨区域的链路，这降低了网络的连通性。

六边形区域边长L的选取也会影响路由算法性能。如果L选取过小，网络的连通性降低，这有可能降低路由的可靠性。另一方面，L选取过大，R的划分太粗糙，每个区域内传感器节点多，这样会增加区域内节点之间的通信开销，增加维护路由相连区域的开销。而且L选取过大，也会导致每个区域内不连通的概率增大。区域内不连通，会使路由算法设计困难，这将在后面的章节介绍。本文先考虑每个区域内的节点组织成的局部网络是连通的情况，然后再介绍区域内不连通情况。

判断区域划分的好坏主要有2个方面，一方面是平面化使删除的链路越少越好；另一方面是区域内聚性越强越好，即区域内任意2节点之间距离越短越好。

令节点的通信距离为r’。为了简化平面化过程，本文令六边形区域边长L大于通信半径，即'Lr≥。这种划分不会对网络的连通性产生影响，并且能最大限度地保留网络连通状态。另外，为了降低区域内不连通概率，减小路由相连区域维护开销，平面化过程应当尽可能选择较小的区域边长。综合以上2方面因素，本文选取区域边长 'Lr= 。

5 区域平面化路由算法

第4节介绍了如何将网络平面化，网络平面化是进行平面地理路由的前提。解决了网络平面化问题后使用多种已有的平面路由算法。本文提出一种针对平面化区域网络的路由算法，称为PGR算法。PGR算法有3种工作模式：节点贪心模式、区域贪心模式和区域周边模式。算法从节点贪心模式开始，节点贪心模式中若存在距离目的节点更近的邻居节点，则将数据分组转发给离目的节点最近的那个邻居节点。若不存在距离目的节点更近的邻居节点，算法进入区域贪心模式。在区域贪心模式中，如果区域的路由相连区域中存在距离目的节点更近的节点，则将数据分组通过区域间传输转发到这个节点所在的区域。如果路由相连区域中不存在距离目的节点更近的节点，则算法进入区域周边模式。在区域周边模式中，将每个六边形小区域看作是一个节点。根据右手定则，区域周边算法将数据分组绕空洞沿空洞边缘区域路由，直到到达一个能够进入区域贪心模式的区域，或者到达一个能够进入节点贪心模式的节点。假设节点s要路由数据分组给目的节点t，平面化区域路由策略1所示。

策略1 平面化区域路由策略

5.1 节点贪心路由模式

节点贪心路由是最基本的路由策略，节点转发数据分组时首先判断是否能进行节点贪心路由。如果转发节点的邻居节点中存在距离目的节点t更近的节点，则将数据分组转发给距离t最近的节点。

5.2 区域贪心路由模式

路由策略只有在节点贪心路由失败时才进入区域贪心路由模式。区域贪心模式如图4所示，黑点表示传感器节点，节点之间的连线表示节点之间存在双向链路。假设节点s有一数据分组要传输到目的节点t，图中节点s没有距离目的节点t更近的邻居节点，算法进入区域贪心模式。在区域贪心模式中，节点s在区域R(s)内存在节点n1与另一个区域内节点n2有链路，且节点n2比节点s距离目的节点更近，因此节点s可以将数据分组通过区域间通信转发给节点n2所在区域R(n2)。

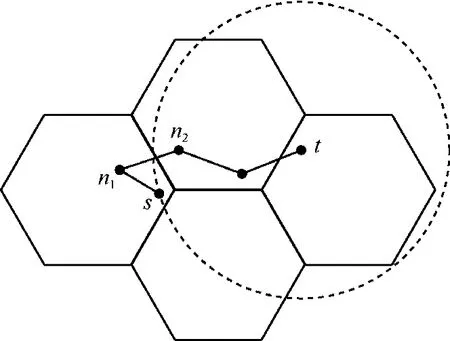
图4 区域贪心路由

通过以上例子，现给出区域贪心模式形式化描述。假设目的节点为t，算法在节点s进入区域贪心模式。节点s所在区域为R(s)，如果 ∃n∈C(s) ∪R(s)，s'∈R(s),使得s'∈CP(s),s'n∈E,且D(n,t)＜D(s,t)，则算法将数据分组转发给使得D(n,t)最小的n所在区域R(n)，其中，D(u,v)为节点u和v间的距离。

5.3 区域周边路由模式

区域周边模式将六边形区域当作一个虚拟节点，虚拟节点的坐标为六边形区域的中心，虚拟节点的路由表中存放的是路由相连区域。以虚拟节点组成的网络是一个平面网络，对于平面网络已有多种算法可实现地理路由算法。

区域周边模式如图5所示，黑色圆点表示节点，阴影部分表示空洞，假设数据分组的目的节点为t，路由算法在节点s区域贪心模式失败进入区域周边模式。连线O(s)O(t)表示源区域R(s)与目的区域R(t)中心的连线。区域周边路由算法以连线O(s)O(t)为基准，使用右手法则逆时针寻找到第一个相邻区域R(v2)并通过区域间通信将数据转发到区域R(v2)。区域R(v2)收到数据分组后以连线O(v2)O(v1)为基准，逆时针寻找到第一个相邻区域R(v3)。如此反复，一直到目的区域，最后通过区域内通信方式将数据分组转发到目的节点。数据分组先后经过的区域如图5箭头所示。

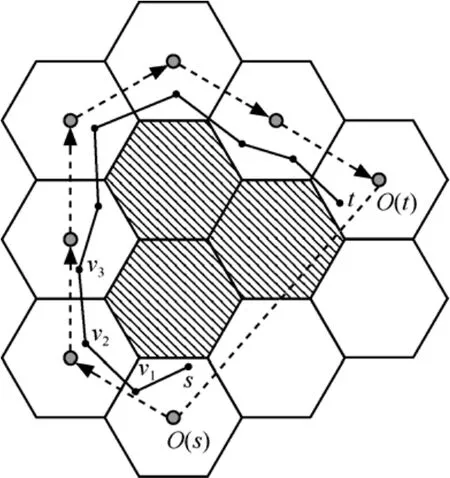
图5 区域周边路由

综上所述，假设节点s要路由数据分组给目的节点t，具体的平面化区域路由策略2如下。

策略2 平面化区域路由策略

6 区域内不连通性

前面给出了平面化方法和地理路由方法。基于六边形网络的平面化方法非常简单，它不需要删除交叉链路，从而最大限度地保留了网络的连通性。以虚拟节点为顶点的平面网络是将六边形区域当成一个整体，因此，现有的平面地理路由算法都可以应用到基于六边形区域划分的平面地理路由中。但是基于区域划分的平面化方法可能会出现区域内不连通情况，如图6所示。在图6中，区域Rs内有2个连通分量CP1和CP2。假设数据分组要从节点s转发到节点t，通过区域周边路由，数据分组会从区域Rs到达区域R1后又回到区域Rs，假设数据分组仍旧返回到连通分量CP1，此时出现路由环。路由环是所有路由算法应该避免的问题。下面给出解决图6所示路由环问题的方法。

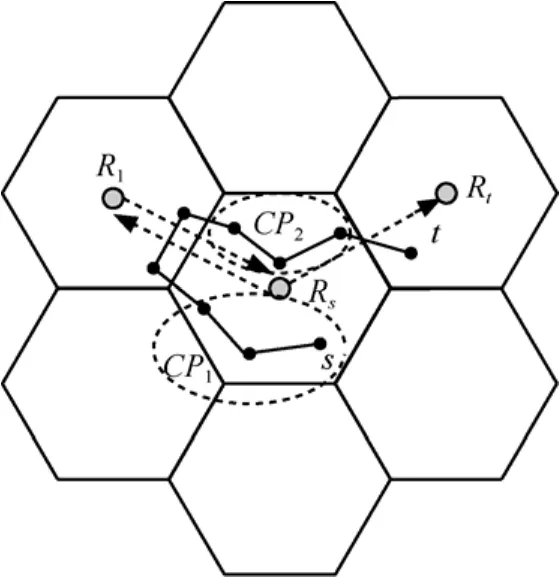
图6 区域内不连通情况

对路由相连区域中每个连通分量给定一个标识(本文以簇头节点号为一个连通分量的标识)。周边模式路由表中每个连通分量都初始化为clean。对于数据分组P，若P从路由相连区域RCi的连通分量CPj转发而来，则将这个连通分量标记为Pin。数据分组若转发给路由相连区域RCi的连通分量CPj，则将这个连通分量标记为Pout。显然，如果向已经被标记为Pout的连通分量转发数据分组，则会发生路由环。因此虚拟节点只能向标记为clean或者Pin的连通分量转发数据分组。并且，虚拟节点应当首先向标记为 clean的连通分量转发数据分组，若找不到标识为clean的连通分量时，才向标记为Pin的连通分量转发数据分组。在向标记为Pin的连通分量转发数据分组时，应对标记为Pin的连通分量按标记时间先后排序，每次寻找时间最靠后的连通分量转发。

除了路由中间区域内不连通，目的节点所在区域也可能不连通。由于任意2个传感器节点之间边长都不超过区域边长，因此数据分组必须通过目的区域的相邻区域才能转发到目的节点。如图7所示，假设数据分组传输到节点s，节点s和目的节点t在同一个区域但不在同一个连通分量，此时让数据分组绕着区域R(s)的相邻区域行走，则可以找到某个与目的节点t所在的连通分量相连的相邻区域。

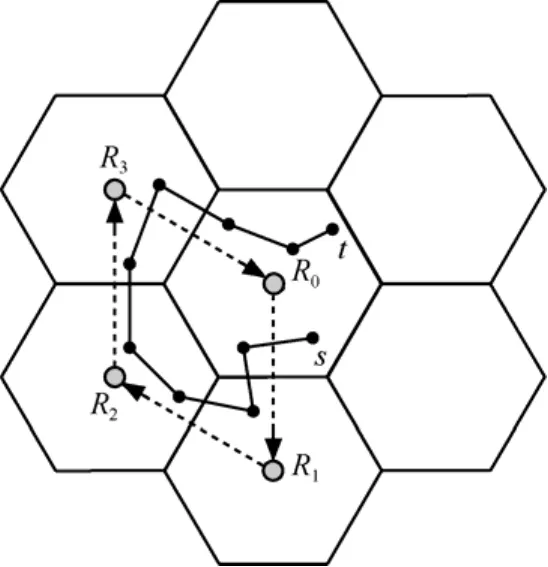
图7 区域内不连通情况

7 区域内不连通概率分析

假设节点是随机布置在一个区域内，则在布置节点之前，任意2个节点间都以一定的概率p可以互相通信，此时所有节点组成的图可以看作一个随机图。给定n个顶点，任意两顶点之间有边的概率为p，则这个随机图不连通的概率的上界qn如式(1)所示[16]。

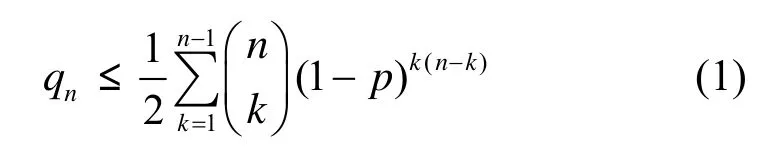
式(1)给出了随机图不连通概率的上界，为了计算qn，还需要给出2个节点间能通信的概率p。

图8给出几种不同通信概率p时随机图不连通的概率。从图可知，在六边形区域内随机布置节点，当区域内节点的个数为2个或3个时，区域内节点不连通的概率最高(注意，区域内不连通和区域间不连通不是一个概念，当区域内节点个数为1时，区域内不连通概率为0)。随着节点个数增加，区域内不连通概率急剧减小，但是当区域内的节点个数达到一定数量后，区域内不连通的概率变化趋于平缓。因此，只要当节点布置达到一定密度后，就能以较高的概率使得区域连通。

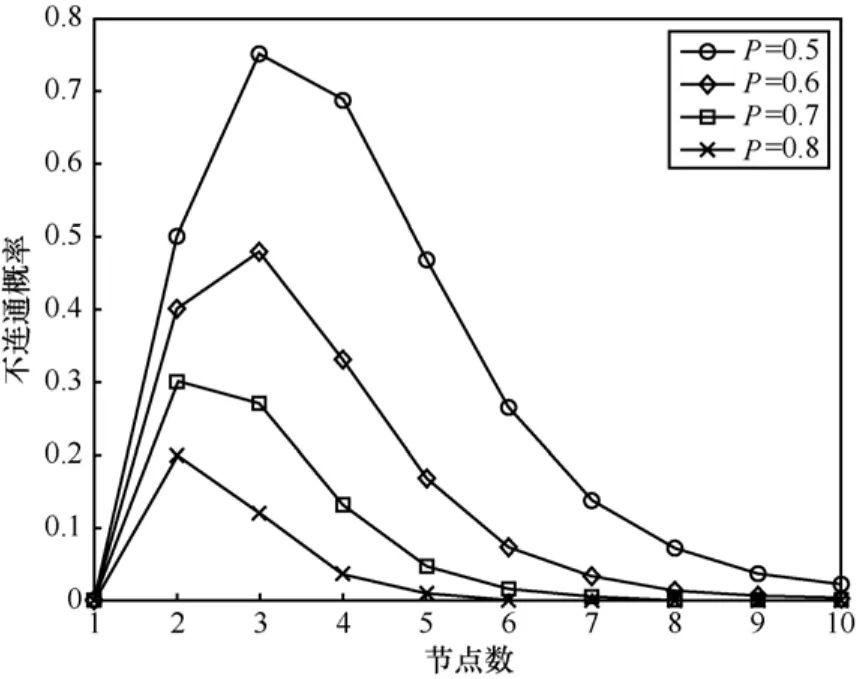
图8 不同通信概率下随机图不连通的概率

假设有n个节点落入了某个六边形区域R0内，则这n个节点在区域R0内也是随机分布的。为了计算区域R0内任意两节点(x1,y1)和(x2,y2)之间距离的分布，如图9所示，节点与某一点v的距离为r的概率为，其中，l是以v为圆心，以r为半径的圆，与六边形区域重叠部分的弧长。任意2个节点之间距离为r的概率分布如式(2)所示。

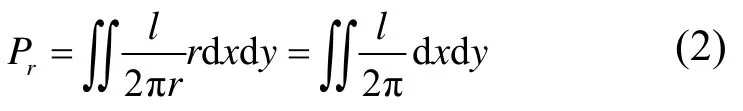
其中，积分区域为六边形区域R0。重叠弧长l随着圆心和半径的变化而变化，不能用一个简单的公式来刻画，因此用数学公式精确计算六边形区域内任意2个点距离r的分布很复杂。本文使用随机算法近似计算两点的距离分布，如图 10所示。在六边形区域内随机选取2个点，并计算这2个点之间的距离，从而得到距离r的分布。

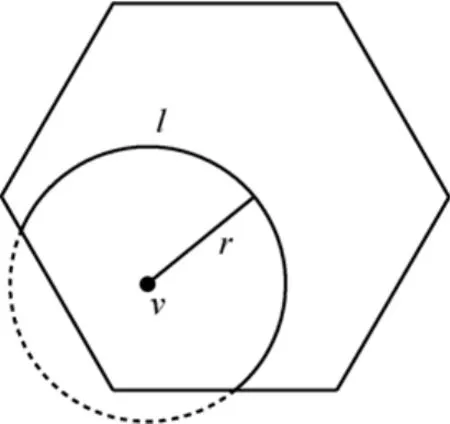
图9 与点v距离为r的点

假设在通信距离内的节点之间都可以互相通信，则区域内2个点能互相通信的概率p(r≤r')=p(r≤L) = 0.65。从而由式(1)得，当区域内落入5个节点时，区域内不连通的概率已经小于9.3%；落入6个节点时，不连通概率小于3.6%。

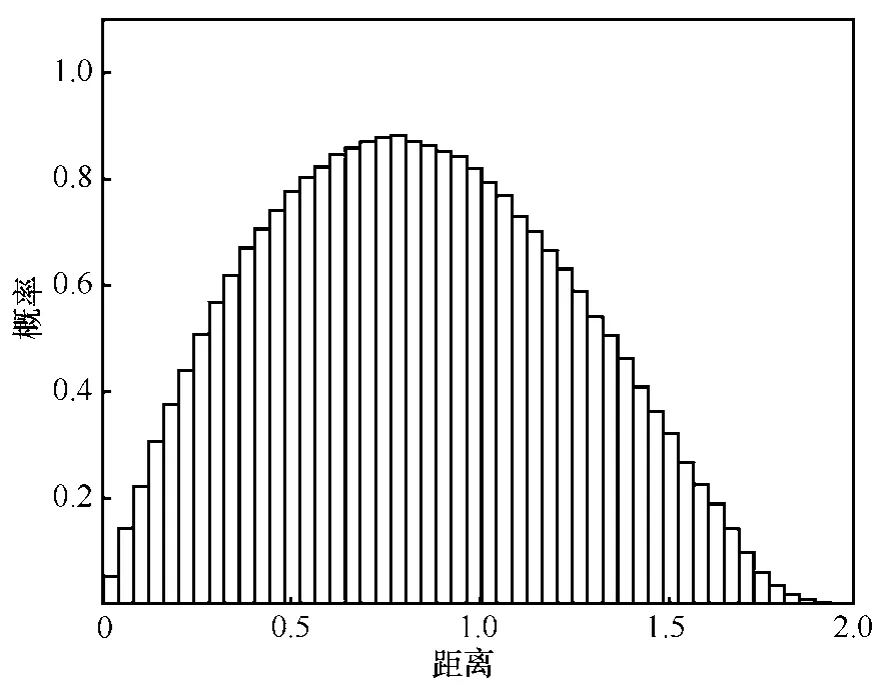
图10 六边形区域内任意2个点距离的概率分布

8 实验结果

目前在真实环境中可用的平面化方法只有交叉链路检测算法（CLDP），但是 CLDP需要检测和删除某些相交链路，增加了路由维护的复杂性。本文提出的方法将网络划分为规则多边形区域，在贪心路由失败时将多边形区域内的所有节点看成一个虚拟节点进行周边路由，它不需要检测和删除相交链路，能够显著减少路由维护开销，提高路由的可靠性。

本文实验使用TOSSIM模拟器结合C++编程语言实现。网络拓扑使用C++随机生成。在给定1 000×1 000大小的区域中随机生成不同节点数和不同通信距离的网络拓扑。本文分别模拟了200、400、600、800和1 000个节点时不同通信距离的路由维护开销以及平均路由路径长度。

以下实验结果中，x轴(n,r)表示1 000×1 000的网络区域内随机布置n个节点，节点间的通信距离为r。如(200, 88)表示整个网络区域内随机布置 200个节点，节点间的通信距离为 88。图11中，不同节点、不同通信距离的实验数据表明，CLDP的路由维护开销明显大于RPR。CLDP的路由维护开销包括探测交叉链路数据分组和删除交叉链路数据分组2种，而RPR的路由维护开销只包括区域内建树数据分组。即使多边形区域内所有节点互相交换信息，RPR平均维护开销也只是多边形区域内节点个数的常数倍。多边形区域内的节点个数越多，路由维护开销增大；反之维护开销减小。只要多边形区域内节点个数不多，RPR的路由维护开销将保持在很低范围内。

图11 CLDP和RPR算法的维护开销比较

CLDP和 RPR路由算法的平均路由长度如图12所示。RPR路由算法中的区域贪心和区域周边模式都是以一个小区域为单位进行路由，因此数据分组在小区域内路由时可以选择优化的局部路由路径，从而减少路由路径长度。本文实验中，RPR路由算法的平均路由路径长度较 CLDP优势不是很明显，其原因是，RPR的区域划分边长选择较小。区域划分边长较小，则每个小区域内的节点个数少，从而可优化的路径选择也少。如果区域划分边长增大，区域内节点个数增多，从而导致区域内不连通概率增大，以及区域内路由维护开销提高，这是RPR路由算法所不希望的。但是区域内节点个数增多，会为区域间通信提供更多的优化路径，从而有效地减少路由路径长度。在网络密度足够高时，适应增长多边形区域边长，能够显著减少路由路径长度。

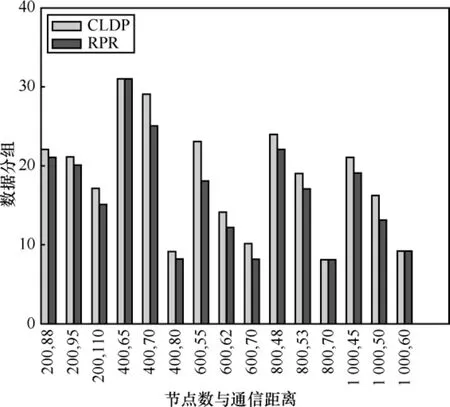
图12 CLDP和RPR的平均路由长度比较

以通信距离为半径的圆内布置的节点越多，其路由的平均长度越小，这是由于通信距离的增大使得贪心路由的比例增大。例如图12中，网络中节点数为600，通信距离分别为55、62和70时，平均路由路径长度逐步降低。当网络节点密度足够高时，贪心路由占主要部分，路由长度显著降低；相反，如果网络节点稀疏，周边路由比例增加导致路由长度增长。

路由成功率和网络中节点密度以及节点的通信距离都有关系，如图 13所示。通常情况下，以通信距离为半径的圆内布置的节点越多，其路由的成功率越高。图13中，以400个节点为例，当通信半径分别为65、70和80时，路由的成功率明显提高；RPR算法的路由成功率比CLDP路由成功率高，其原因是RPR算法中多边形区域内节点知道几跳内邻居节点信息，从而提高区域贪心路由和区域周边路由成功率。

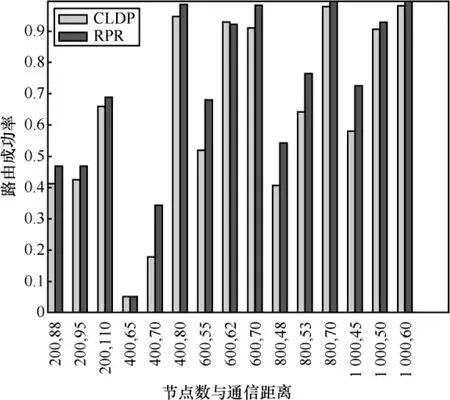
图13 CLDP和RPR的路由成功率比较

9 结束语

目前的地理路由算法都共同面临网络平面化问题。现有的平面化算法大多都假设节点的通信半径固定，然而这种假设在真实的网络环境下不合理。CLDP算法需要检测和删除某些相交链路，增加了路由维护成本。本文提出的基于区域划分的平面化方法，将网络划分为规则多边形区域，它不需要检测和删除相交链路，从而降低路由维护开销。而且，在区域贪心和区域周边2种模式中，算法以小区域作为路由的基本单元，能够减短路由平均路径长度，提高路由的可靠性。

[1] 李建中, 李金宝, 石胜飞. 传感器网络及其数据管理的概念、问题与进展[J]. 软件学报, 2003, 14 (10): 1717-1727.LI J Z, LI J B, SHI S F. Concepts, issues and advance of sensor networks and data management of sensor networks[J]. Journal of Software, 2003, 14 (10): 1717-1727.

[2] 孙利民, 李建中, 陈渝等. 无线传感器网络[M]. 北京: 清华大学出版社, 2005.SUN L M, LI J Z, CHEN Y,et al. Wireless Sensor Networks[M]. Beijing: Tsinghua University, Press, 2005.

[3] KARP B, KUNG H T. GPSR: greedy perimeter stateless routing for wireless networks[A]. Mobicom'00[C]. Boston, Massachusetts, USA, 2000.

[4] FREY H, STOJMENOVIC I. On delivery guarantees of face and combined greedy-face routing in ad hoc and sensor networks[A]. MobiCom’06[C].Los Angeles, CA, USA, 2006. 390-401.

[5] KIM Y J, GOVINDAN R, KARP B. Geographic routing made practical[A]. Proc of USENIX Symposium on Network Systems Design and Implementation[C]. Boston, Massachusetts, USA, 2005.

[6] BOSE P, MORIN P, STOJMENOVIC I. Routing with guaranteed delivery in ad hoc wireless networks[A]. 3rd Int Workshop on Discrete Algorithms and Methods for Mobile Computing and Communications[C]. Seattle, USA, 1999. 48-55.

[7] KRANAKIS E, SINGH H, URRUTIA J. Compass routing on geometric networks[A]. Proc of the 11th Canadian Conference on Computational Geometry (CCCG’99)[C]. Vancouver, Canada, 1999. 51-54

[8] KUHN F, WATTENHOFER R, ZHANG Y. Geometric ad-hoc routing:Of theory and practice[A]. Proc of the 22nd ACM Int. Symposium on the Principles of Distributed Computing (PODC)[C]. Boston, Massachusetts, USA, 2003.

[9] KUHN F, WATTENHOFER R, ZOLLINGER A. Worst-case optimal and average-case efficient geometric ad-hoc routing[A]. Proc of the 4th ACM International Symposium on Mobile Computing and Networking (MobiHoc 2003)[C]. Annapolis, Maryland, USA, 2003.

[10] LEONG B, MITRA S, LISKOV B. Path vector face routing: geographic routing with local face information[A]. Proc of the 13th IEEE International Conference on Network Protocols (ICNP'05)[C]. Boston,Massachusetts, USA, 2005. 147-158.

[11] GABRIEL K R, SOKAL R R. A new statistical approach to geographic variation analysis[J]. Systematic Zoology, 1969,18: 259-278.

[12] TOUSSAINT G. The relative neighborhood graph of a finite planar set[J]. Pattern Recognition, 1980 , 12(4): 261-268.

[13] LI X Y, CALINESCU G, WAN P J. Distributed construction of a planar spanner and routing for ad hoc wireless networks[A]. Proceedings of the 21st Annual Joint Conference of the IEEE Computer and Communications Society (INFOCOM’02)[C]. New York, USA, 2002.1268-1277.

[14] KIM Y J, GOVINDAN R, KARP B. Lazy cross-link removal for geographic routing[A]. Proc of the 4th International conference on Embedded Networked Sensor Systems[C]. Boulder, Colorado, USA,2006. 112-124.

[15] TIAN H, SHEN H, MATSUZAWA T. Developing energy-efficient topologies and routing for wireless sensor networks[A]. Proc of International Conference on Network and Parallel Computing[C]. Beijing,China, 2005.

[16] GILBERT E N. Random graphs[J]. Ann Math Statist, 1959, 30(4):1141-1144.