针对可扩展交换网络的顽健性评价方法

杨光辉，吴建平，赵有健，孙书韬

(1. 清华大学 计算机科学与技术系，北京 100084；2. 中国传媒大学 计算机学院，北京 100024)

1 引言

随着规模和用户持续高速增长，互联网已经演变成为一个全球性通用网络。互联网技术也因受到需求的驱动得到了长足的发展，各种应运而生的新型业务和协议已经在互联网中大规模的部署。互联网中的流量正以指数级别的速率增长。这些状况对互联网核心路由器提出了许多新的要求，包括提供更多更高速的端口设备以及更大的交换容量等。目前互联网的核心路由器一般采用集中式体系结构。这种体系结构虽然便于对需要转发的数据流量进行调度，但限制了路由器交换容量的扩展以及端口的数量增长[1]。为了解决这一问题，基于分布式体系结构的可扩展路由器被提出并得到越来越多的关注和研究[2]。

交换网络是路由器的关键部件。目前大多数商用路由器中，交换网络被设计为固定专用部件，扩展性较差。例如，共享总线交换结构中各个端口所共享的总线带宽是扩展的瓶颈。基于交叉开关（crossbar）的交换结构的扩展受到crossbar规模限制，扩展代价较大，接近于O(N2)级别（N为交换结构的端口数量）。交换网络的扩展性直接决定了路由器的扩展性，具备较好规模扩展能力的交换网络称为可扩展交换网络。可扩展交换网络可以分为多级互连网络[3,4]（MIN, multistage interconnection network）、直连交换网络[5～7]（DN, direct switch network）、以及混合交换网络[8]。由于混合交换网络结构复杂，在路由器实际设计中少有采用，因此在本文中可扩展交换网络特指MIN和DN 2类。

无论MIN或DN都可抽象为连接图。连接图是将一定数量的节点（交换单元）通过边（链路）连接起来的抽象图。下文中将边和节点视为连接图的组件。MIN抽象图和 DN抽象图存在一定区别。MIN抽象图中的节点可以分为2类：一类为输入/输出端口节点（简称端口节点），另一类为交换单元节点。外部数据流量通过输入端口节点注入路由器交换网络，再通过交换单元节点转发到输出端口节点。与MIN抽象图不同，DN抽象图中的每个节点既是端口节点，又是交换单元节点。DN节点可以接收目的是本节点的数据流量，也可将目的是其他节点的数据流量根据策略进行转发。随着组件数量的不断增大，整个交换网络的联合故障概率必然会随着规模扩展而不断变大。因此可扩展交换网络的设计必须考虑可能发生的组件故障对交换网络的影响。

故障对网络的影响一般采用基于顽健性的评价指标。对于一个网络，顽健性是当部分网络拓扑组件发生故障后，该网络保持基本功能的能力。根据基本功能的不同，顽健性评价方法可以分为2类[9]：一类方法的评价指标关注图的连通性，另一类的评价指标关注节点间距离的变化。可扩展交换网络的拓扑不仅可以决定一个交换网络的吞吐率、延迟等性能的上限，其顽健性也直接决定着可扩展路由器可靠性[10]。因此，合适的评价方法可以区别出不同可扩展交换网络顽健性差别，这对于可扩展交换网络的设计具有重要意义。

MIN类可扩展交换网络的顽健性适宜采用基于连通性指标的评价方法；DN类可扩展交换网络的顽健性则更适合采用基于距离指标的评价方法。目前研究中基于距离的评价指标多采用直径以及直径变化[11]等全局信息，这些指标应用于DN的顽健性评价存在以下问题：第一，直径类评价方法不能在少数组件随机发生故障的情况下对DN进行顽健性评价；第二，现有评价方法的算法复杂度较高。可扩展交换网络的顽健性评估需要根据评估的规模重复运行评估算法，此时评价方法的复杂度问题尤其突出。

本文内容安排如下。第2节中研究可扩展交换网络的拓扑特点以及随机故障模型，并建立模型比较DN在不同故障模型下的顽健性差别。提出一种新的基于故障影响（failure influence）的顽健性评价方法，故障影响包含的2种评价指标:故障影响范围（FIS, failure influence scope）和故障影响强度（FII,failure influence intensity）。第3节提出故障评价方法的优化算法。第4节分析和对比一些主流可扩展交换网络的故障影响属性。第5节是结束语。

2 针对可扩展直连网络故障影响的顽健性评价方法

失效、故障和错误的概念在容错计算领域中有着详细的区分。失效是指各种物理现象，如链路中的高斯噪声、导体中的电子迁移、供电系统异常等现象。故障是失效的表现形式[12]，如供电异常（失效）导致某寄存器无法保存数据，则这种行为定义为寄存器故障。这个故障致使计算机无法使用该寄存器导致计算结果偏离正常，最终表现为计算机错误。本文的研究主要针对组件层面（交换节点、链路等），以下统一采用故障进行表述。针对可扩展交换网络的顽健性评估方法必须考虑2个问题：首先，评价方法必须基于可扩展交换网络的应用场景；其次，评价方法必须可以区别不同可扩展交换网络顽健性的差别。

2.1 可扩展直连交换网络顽健性评价的需求分析

2.1.1 随机故障模型

故障模型对故障产生的类型、故障持续的长短和故障在系统中的分布以及系统中设备出现故障所服从的统计规律等进行具体的规定[13]。可扩展交换网络在运行过程中可能产生多种故障，例如硬件故障，软件运行时出现的漏洞导致的异常，流量导致的缓存溢出异常等。这些来源不同的故障从抽象图的角度可以归纳为节点故障、边故障、混合故障（边故障和节点故障同时存在）。根据故障持续时间可以划分为瞬态故障、永久故障、间歇型故障等。如果在故障产生后不能利用设备的冗余资源进行恢复，那么值守人员对该故障进行人工恢复的时间一般为小时级别甚至更长，这种故障定义为永久故障。

2类最常使用的故障模型包括界限模型（bounded model）和概率模型（probabilistic model）[14]。界限模型设定了发生故障的节点/边的上界值，以最坏情况进行分析。概率模型中故障的发生概率是随机且相互独立的。本文针对的随机故障模型属于概率模型。在随机故障模型中假设基于严格正交拓扑的可扩展交换网络抽象图中的节点或边发生故障的概率是相同的，并且各个节点或边的故障概率相互独立。随机故障模型常用于可扩展交换网络的顽健性研究中[9]。系统的一次随机故障记为f(i)，其中，i为故障组件的数量。根据发生故障的组件不同，随机故障模型又可分为随机节点故障模型（记为fv(i)）、随机边故障模型（记为fe(i)）、随机混合故障模型（记为fh(i)）。随着微电子技术的进步以及路由器的广泛应用，路由设备专用芯片已经非常成熟，多个组件同一时刻发生故障的概率非常小。因此，小规模的组件同时发生故障的情况在可扩展交换网络随机故障模型中占主要地位。

2.1.2 DN和MIN顽健性评价方法的区别

将DN和MIN抽象为连接图，二者最大的不同在于DN的交换单元和输入输出端口结合并采用严格正交拓扑连接，而 MIN的输入输出端口则分离且其交换单元以分级方式连接。DN和MIN在顽健性方面也有明显的差别。以24节点Benes（MIN，图1(a))和25节点2D-Torus (DN，图1(b))为例。该Benes网络的交换单元节点分为6级，每一个输入输出端口对之间都存在多条路径。例如，如果有数据分组需要从C0(6)转发到C6(7)，图1(a)存在8条路径可选。如果节点G1(2)发生故障（在图1(a)中以矩形阴影表示），那么仍有其他长度为 6的路径可选。对于MIN，只要输入输出端口对是可达的，从源到目的节点的路径长度将不受影响。因此，基于连通指标的评价方法相比于基于路径长度指标的顽健性评价方法更适用于MIN。通过观察易得，DN的任意端口对间的路径数目远大于MIN，这使得少量的故障很难对DN的连通性产生影响。但由于路径长度是不等的，因此基于路径长度指标的顽健性评价方法更适宜于DN。

基于连通性指标的顽健性评价方法的研究成果较多，例如文献[8,15]中提出了适用于MIN的连通性评价指标。而基于路径长度指标的顽健性评价方法较少，下文将分析现有基于路径长度指标是否适用于可扩展交换网络的顽健性评价。网络的顽健性依赖于故障模型，不同故障模型会对网络的顽健性产生不同的影响。根据本文的调研，现有文献中较少结合随机故障模型对DN进行顽健性分析。下文将通过定义和证明来分析DN在随机故障模型下的顽健性。

定义1 在图G(V,E)中，V为节点集合，E为边的集合。图G(V,E)的K子集定义为G中任意的K个节点，且K个节点之间有边连接，亦称为G的K子图。Vk是G中非K子集节点且与K子集的节点有边连接的节点数目，亦称为K子集的邻居节点数。Sk是G中K子集的总数。如果G中所有节点的度等于δ，且满足对任意1＜K＜N/2存在VK-δ≥2，那么图G称为一个δ-规则图。

定义2 图G为非连通图当且仅当图中存在子集被从G中隔离开。其中几种事件的概率如下。

P(i)：图G中发生i个组件故障后变成非连通图的概率。

Q(i)：在i-1个故障时是连通图，然后移除一个节点后，变为非连通图的概率。

Qk(i)：图G在i-1个故障时是连通图，产生任意一个节点故障，在i个故障后从G中隔离出一个K子图概率。

上述几种概率满足以下 2个关系：①P(i)=，这个公式的含义是在发生第i个故障后变为非连通图的概率等于发生1到i-1个故障都不会变成非连通图的概率和第i个故障后正好变成非连通图概率的乘积。这个公式的含义是在第i个故障后变为非连通图的概率等于在第i个故障后隔离出所有可能的K子图概率之和，其中，Max代表在i故障下K子图所有可能值。

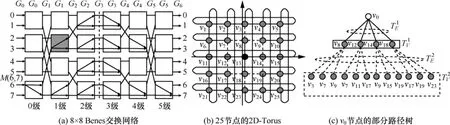
图1 以Benes网和2D-Torus网举例说明MIN和DN

分别记只有节点发生随机故障、只有边发生随机故障以及边和节点都发生随机故障的C(G)为Cv(G)、Ce(G)以及Ch(G)。假设图G的节点数N远大于δ，首先分析Cv(G)。在只有节点发生随机故障时，在N远大于δ的假设下，利用斯特林公式对上式中的阶乘进行化简。可以得出从定义2分析可以得出：Sk是O(N)级别的数，而Vk是O(δ)级别的数，可以推出Sk远大于Vk。当K＞1时，可得：

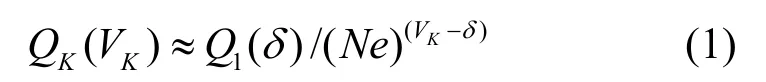
由定义2可知，VK-δ≥2，且N远大于δ，将式(1)代入Cv(G)可以得到：

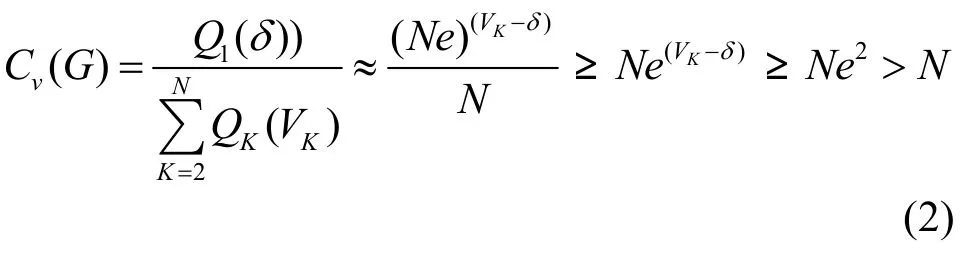
根据式(1)可知，在随机节点故障模型下Cv(G)随着N增大而增大，G的连通性也随之增强。因此，随着规模增大，连通性指标对于δ-规则图的评价效果逐渐变差。下面的分析主要针对Ce(G)和Ch(G)，化简中用到的技巧与式(1)的推导过程类似，为了节省篇幅，下文中简要给出Ce(G)和Ch(G)的分析过程。

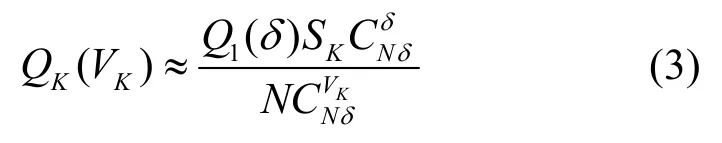
Ce(G)推导中采用随机边故障模型，因此式(2)中加入组合数CδNδ，表示从所有的Nδ个边中选取δ个边，代表单个节点被隔离的情况。K子图被隔离的情况与式(1)中表述相同。应用VK-δ≥2和N远大于δ，易得出。采用类似式(1)的化简过程，将式(2)代入Ce(G)中，可以得出Ce(G) ＞Cv(G) ＞N。

在混合故障模型下产生故障的组件既有节点也有边。式(4)表示l个边故障，其中，通过组合数之间的比较很容易得出式(5)，在此不再做详细的证明。

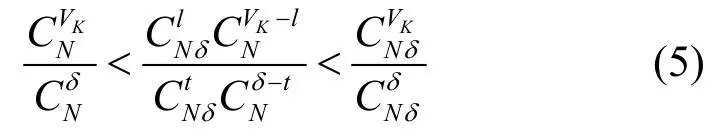
考虑到混合随机故障模型的定义，其中，故障应包含所有边故障和节点故障的组合，则由式(4)和式(5)可得式(6)。

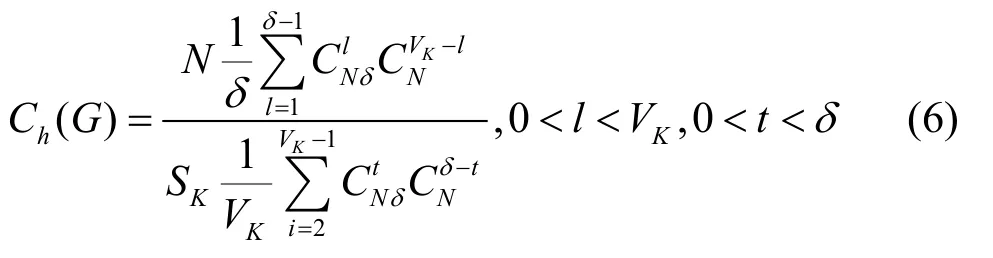
结合式(4)和式(5)，利用和推导式(2)相同的化简方法，可得Cv(G)＜Ch(G)＜Ce(G)。根据式(2)、式(4)和式(6)可以得出：无论在随机边故障模型、随机节点故障模型还是随机混合故障模型，上述证明说明随机节点故障模型对顽健性的影响最大，随机混合故障模型次之，随机边故障模型对δ-规则图的顽健性影响最小。这说明图的顽健性研究只需基于随机节点故障模型和随机边故障模型，这2种模型下的顽健性评价效果将是混合故障模型下评价效果的上下界。

2.1.3 现有评价尺度对于DN的不足

在节点规模相同情况下，MIN任意输入输出端口对间的路径数量远小于 DN。采用已有文献[8,15]提出的评价方法，例如网络可靠性、终端可靠性和广播可靠性等基于连通指标的顽健性评价方法能够很好地对MIN类的网络进行评价。已有研究中针对 DN的顽健性评价一般采用直径类指标。直径为图G中任意节点对之间距离的最大值。直径类指标的评价效果依赖于故障模型。在以一定故障数来产生最大破坏能力的界限模型下，直径类指标能够较好显示出顽健性的变化[11]。但如果在随机故障模型下，直径类指标并不能对δ-规则图进行有效的顽健性评价。

以2种典型的DN即2D-Torus和3D-Torus为例，在随机故障模型下验证直径增量指标的评价效果。由 2.1.2节的证明可知混合故障模型的顽健性处于随机节点故障模型和随机边故障模型之间，因此只选择后2种故障模型进行研究。图2(a)和图2(b)分别说明了2D-Torus在随机边故障模型和随机节点模型下直径的变化。在节点规模达到100的时候，直径随着故障数量增加的变化非常小。这种趋势在3D-Torus上更加明显（如图2(c)和图2(d)所示）直径变化趋势已经成为水平直线。上述实验结果表明直径类指标无法对DN进行顽健性评价。因此必需在随机故障模型下设计一种有效的DN顽健性评价方法。

2.2 基于故障影响顽健性评价方法

2.2.1 故障影响评价方法的设计动机

目前，研究和应用较多的DN包括n维全连接网络、链形网络、回环网络(torus)和超立方网络等。DN一般采用严格正交拓扑，原因在于：首先，当网络规模持续增大时，严格正交拓扑易于保持固有的良好属性。其次，统一设备规格可以使制造、维护以及更新设备的成本大大降低。少量故障对 DN造成大规模节点被隔离的概率非常低。更可能的情况是，少量组件故障只是某些节点对间的最短路径长度增加，这类似于一场地震。地震会对地面建筑或人员造成较大的破坏，距离震中越近的区域这种破坏效果越明显。地震可以用等震线在地图中表示，这种方法可以较为清晰地显示一场地震的破坏力及其影响范围。

借鉴地震破坏力的评价方法，本文针对基于DN的可扩展交换网络提出了一种新的顽健性评价方法，命名为故障影响。这种方法较直径类的评价方法不同之处在于评价指标的选取。直径类指标关注于发生故障后图的某种全局特征的变化。但少量组件故障很可能难以导致全局特征的变化。故障影响评价方法将故障抽象视为震中，并评价该故障对于整个网络产生的破坏力。与震级和等震线的概念类似，故障影响包含2种不同评价指标：故障影响强度(FII, fault influence intensity)和故障影响范围(FIS, fault influence scope)。下文将对故障影响的评价指标进行描述。

图2 多种规模Torus网络在随机故障下的直径变化趋势

2.2.2 故障影响评价方法的基本定义

针对随机故障模型，在文中采用fe(G,k)代表图G中同时产生故障的k个边。同理，fv(G,k)代表图G中同时产生故障的k个节点，fh(G,k)代表图G中同时产生故障的k个节点或边，f(G,k)代表图G中同时产生的k个任意来源故障。在δ-规则图G(V,E)中，当发生一次k规模故障f(G,k)后，G′为从G移去故障节点和边后的图。

定义3 节点的级和边的级。在δ-规则图G(V,E)中，任选一个节点v0作为起始节点，v0的级定义为 0，记为Nl(v0)=0。假设vi(i≠0,vi∈V)距离v0的最短路径长度为k，则vi的级为k，记为Nl(vk)=k。图G(V,E)中所有级为k的节点组成的集合记为。G(V,E)中的va和vb之间如果存在一条边，那么这条边记为eab，eab的级记为El(eab)，El(eab)=max(Nl(va),Nl(vb))。所有级为l的边组成的边的集合记为图1(c)以虚线框标识了

定义4 最短路径长度矩阵 (OM, one to all shortest path matrix)。在δ-规则图G(V,E)中，节点vi到G中其余所有节点vj(i≠j,vj∈V)的最短路径的长度值形成N-1个元素的一维向量，记为OM(G,vi)。假设当G(V,E)中产生故障f(G,k)后拓扑变为图G'(V',E')，对于vi(vi∈V，vi∈V)，如OM(G,vi)≠OM(G′,vi)，则vi定义为G中被故障f(G,k)影响的节点。其中，OM(G,vi)和OM(G',vi)只比较vi到正常节点的距离变化。

定义5 在δ-规则图G(V，E)中，当发生一次k规模故障f(G,k)后，G的拓扑变为G'。G'中被故障f(G,k)影响的节点的最大数量称为f(G,k)的故障影响范围，记为FFIS(f(G,k))。

定义6'

G中被故障f(G,k)影响的节点集合记为对于为2个N-1个元素的一维矩阵差值中的最大值，记为Mmax(G′,vi)。其中，OM(G,vi)和OM(G′,vi)只比较vi到正常节点的距离变化。FFII(f(G,k) )的值为

以图3为例，节点15在某一时刻产生了故障，即fv(G,1)={15}。由于节点的规模较小，通过观察就可以得出在其余节点中，节点最短路径长度矩阵发生变化的节点是{v4,v7,v8,v9,v14}。根据定义5，FIS(fv(G，1))=5。{v4,v7,v8,v9,v14}这些受影响点的Mmax(G',vi)值则分别为{1,1,1,1,1}。因此FFII(f(G,k) ) = 1 。

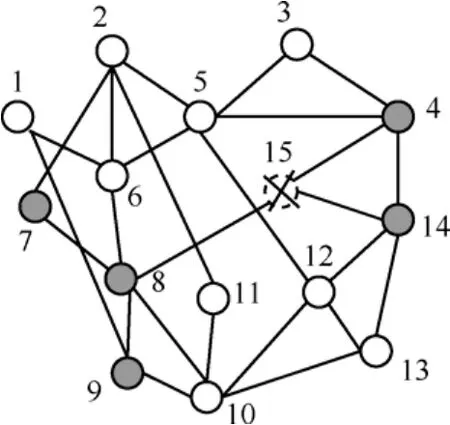
图3 网络故障

2.2.3 评价方法的算法简化

图的顽健性评价算法一般具有很高的复杂度，其中，大部分评估算法都不具备多项式级别的评估算法。如 Minimumm-Degree[16]、Fragmentation[17]、Persistence[18]等评价估算法，在文献[9]中已经归纳并证明了多数顽健性评价尺度的评估算法是 NP-hard难度。在实际的网络运营环境中，运营商会根据需要变更可扩展路由器的规模。规模扩展的灵活性要求顽健性评价方法应能评价顽健性随规模变化的趋势，这需要对可能应用到的规模都运行评价算法进行顽健性分析，此时算法复杂度的重要性更加凸显。因此，简化评价算法复杂性非常重要。

FIS和FII都是基于距离的评价指标。如果基于经典最短距离算法Dijsktra，节点的OM算法的复杂度应为O(N4)。考虑所有可能的节点规模，OM算法的复杂度增加为O(N5)。FIS和 FII都是针对δ-规则图设计的。文献[11]证明，在一个严格正交的网络中，故障对其邻居节点集合(记为VN(f(G,k)))的连通性产生最大的影响。这个结论可以应用于简化FII，如式(7)所示。假设VN(f(G,k))＜＜N，FII的评价算法的复杂度可以降低为O(N4)。

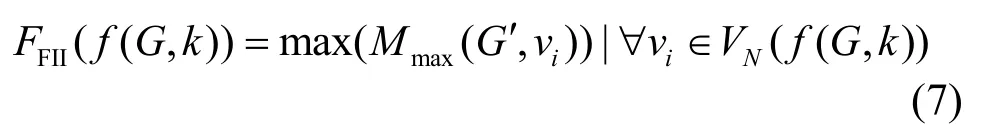
3 直连交换网络的故障影响分析

3.1 几种流行的直连网络

常用的流行直连交换网络包括：环型拓扑、星型拓扑、立方体型（cubes）、回环图型等。首先对结构相对简单的环型和回环型拓扑进行随机单故障模型的故障影响分析。从定义1可以得出，虽然环型拓扑是点对称的，但因为VK-δ＜0，所以环型不属于δ-规则图。环型和回环型的故障影响分析由于其拓扑特征而具有相似性，环型拓扑或回环拓扑中的环可以按照节点个数的奇偶性分为2类：偶环和奇环。通过观察和归纳易得出环的边故障影响范围。为节省篇幅，下文直接给环型和回环型的单边故障影响的研究结果，如表1所示。

表1 环型拓扑和回环型拓扑的FIS和FII属性

文献[19]对严格正交拓扑进行分析后得出结论：在严格正交连接网络中，如果节点的度固定且内部链路带宽固定，则其吞吐率将随节点规模增大而最终下降。这个结论说明，如果要实现理论意义上的规模无限可扩展，节点度必然需要随着节点规模扩大而增长，否则内部带宽将成为吞吐率增长瓶颈；另一方面，节点的度不能过大，否则将导致扩展成本增大。为了平衡这对矛盾，本文前期工作在文献[1]中提出了渐进最小度扩展的可扩展交换网络P2i。P2i具有直径小、灵活扩展粒度、等分带宽较大等优点。

3.2 P2i的故障影响分析

3.2.1 拓扑概述

P2i可以抽象为连接图G=(V,E)。设N为节点的总数，所有节点从0至N-1编号。编号v的节点拥有条入边。节点v的各条出边依次称为0维边至1δ-维边。i维边（记为i-dim）连接编号为(v+2i)modN的节点。1δ-维边亦记为HD边，其余出边记为non-HD边。图4为8节点和9节点的P2i。

定义7 跨度(span)：在一个N节点的P2i中，如果在va和vb之间存在一条边eab，则eab的跨度记为dspan(eab)，且dspan(eab)=((b-a)+N)modN。va和vb间如存在一条最短路径P，则va和vb的跨度记为dspan(va,vb)，并且

定义8 在N节点的P2i中，va和vb之间的最短路径如果只包含non-HD边，那么这种最短路径记为NHSP。如果只包含HD边，那么这类最短路径记为 HDSP。如果最短路径中既有 HD边又有non-HD边，则记为HYSP。HYSP的路径长度应大于等于2。如果va和vb间存在多于2条的最短路径，那么这些路径互相称为对称路径。

图4 一个8节点P2i和一个9节点P2i

3.2.2 P2i故障影响的相关结论

结论1 任取一个N节点的P2i中的节点v0，从v0到其他节点的一条最短路径中，跨度为2i(i＜δ-1)的边最多只能包含一次。

结论 2 可以通过反证法来证明。当路径长度为1的时候，结论显然成立。跨度为2i(i＜δ-1)的边属于non-HD。当路径长度大于2的时候，如果跨度为2i(i＜δ-1)的边出现了2次，则必然能找到一条跨度为dspan((i+1)-dim)=2，dspan(i-dim)的i+1维边将代替两条i维边，形成一条新的最短路径P'，并且P'的路径长度小于P，则P为最短路径的假设不成立。据此，结论1得证。

结论3 在一个N节点P2i中，假设从va到vb存在一条路径长度大于1的最短路径P，并且P是NHSP或者HYSP中的任一种，则P必然存在一条对称路径P'，并且P'和P是边不相交的。

在一个N节点规模的P2i中的最短路径，如图4(a)的 8节点 P2i中，从v0到v3的一条最短路径v0→v2→v3，这条路径可以用一个节点序列表示为(v0,v2,v3)，也可以表示为一个边的序列(e0,2,e2,3)或者一个跨度值的序列(1,0)。如果P为NHSP并且P的路径长度大于1，则跨度值序列至少有2个位置的元素必然是不同的。在上述例子中跨度值的序列(1,0)，必然还存在着另外一种跨度值的序列(0,1)。路径长度越大，跨度值的排列越多，这意味着对称路径的数量也就越多。由于跨度值排列数不同，则节点序列不同，因此边的序列也是不相同的，即为边不相交的。结论2得证。

结论4 在一个N节点P2i中，non-HD的随机单边故障的故障影响范围为1，P2i的随机单边故障的故障影响范围等于HD边的单边随机故障的影响范围。

任取一个N节点P2i中的节点v0。在随机单故障模型下，如果故障发生在v0的1级边，则OM(v0)必然会改变。如果故障边为非1级边，则故障边可以分为2种：HD边和non-HD边。如果故障边为non-HD边，根据结论2，OM(v0)不会变化。则non-HD边在随机单故障模型下故障影响范围为 1。如果在故障边为HD边的情况下，由于P2i边的不对称性，HD边的故障影响范围大于等于 1。因此，根据定义6可知P2i的随机单边故障的故障影响范围等于HD边的故障影响范围。

结论5 不失一般性，任取一个N节点P2i中的节点v0，HD边故障只可能会影响到v0到其他节点的HDSP最短路径的长度。

v0到其他节点的最短路径中包含HD边的只可能是HDSP和HYSP二者之一。假设从v0到vb存在一条HYSP最短路径P。显然HYSP的路径长度大于等于2，根据结论2，P存在一条对称路径P'，OM(v0)不会改变，因此结论4得证。

3.2.3 P2i故障影响的优化算法

任取一个N节点P2i的节点v0，存在一个正整数k，当HDSP的路径长度大于或等于k+1时，v0通过这条HDSP路径连接了vk，则v0到vk必然存在一条长度小于等于k+1的NHSP，k称为P2i的阈值。根据结论3可知阈值就是P2i在单随机故障模型下的FIS值。据此只需采用启发式算法求得P2i中的阈值即可得到该P2i的FIS值。上述启发式算法可以由以下的伪代码进行描述。其中，SPF(vs,vd)表示从vs到vd最短路径的长度，vs,HD表示vs第1δ-维边所连接的节点。k是一个初始值为0的变量，FIS的初值为0。

4 实验结果及比较

在第 2节中提到，顽健性评价方法首先必须基于可扩展交换网络的应用场景；其次，该方法必须可以区别不同可扩展交换网络的顽健性差别。本节将通过 3个实验来检验故障影响评价方法是否满足上述2个标准。根据2.1.1节的论述，本节所有实验都基于随机故障模型以符合可扩展交换网络的应用场景。下文首先通过敏感性实验来检验故障影响评价方法是否能在随机故障模型下对大规模可扩展交换网络进行顽健性评价。其次，用单故障实验和相近连接网络故障属性实验来检验故障影响评价方法能否区别不同可扩展交换网络的顽健性差别。

4.1 敏感性实验结果及分析

实验采用随机从所有组件中选取故障组件的方式。为了近似地实现随机性，实验中采用随机故障分布模式。例如，假设节点的随机故障概率为1%，在1 000个节点规模时，应有10个节点发生故障。随机从1 000个节点中选取10个节点，称为一次故障分布模式。第4节所有实验均随机选取10 000种故障分布。本节实验只选取Edge-FIS评价指标对不同种类DN进行分析，目的在于对比故障影响评价指标和直径类评价指标在少量组件故障下能否敏感反映顽健性的变化。

图5(a)的实验分别选择了27节点（记为3D-27横坐标采用 log坐标）、125节点、343节点、729节点的3D-Torus。在发生故障的组件逐渐增加的情况下对比直径的增量和 Edge-FIS指标的变化。图5(a)中各条虚线为直径增量评价结果。实验结果表明，直径类指标几乎毫无变化，在图5(a)中显示为近似水平直线，显然无法反映网络顽健性的变化。相反地，从图5(a)中可以看出，即使网络规模增大到 729，故障影响指标的变化依旧明显。这表明故障影响指标能够敏感的反映大规模可扩展交换网络顽健性的变化。

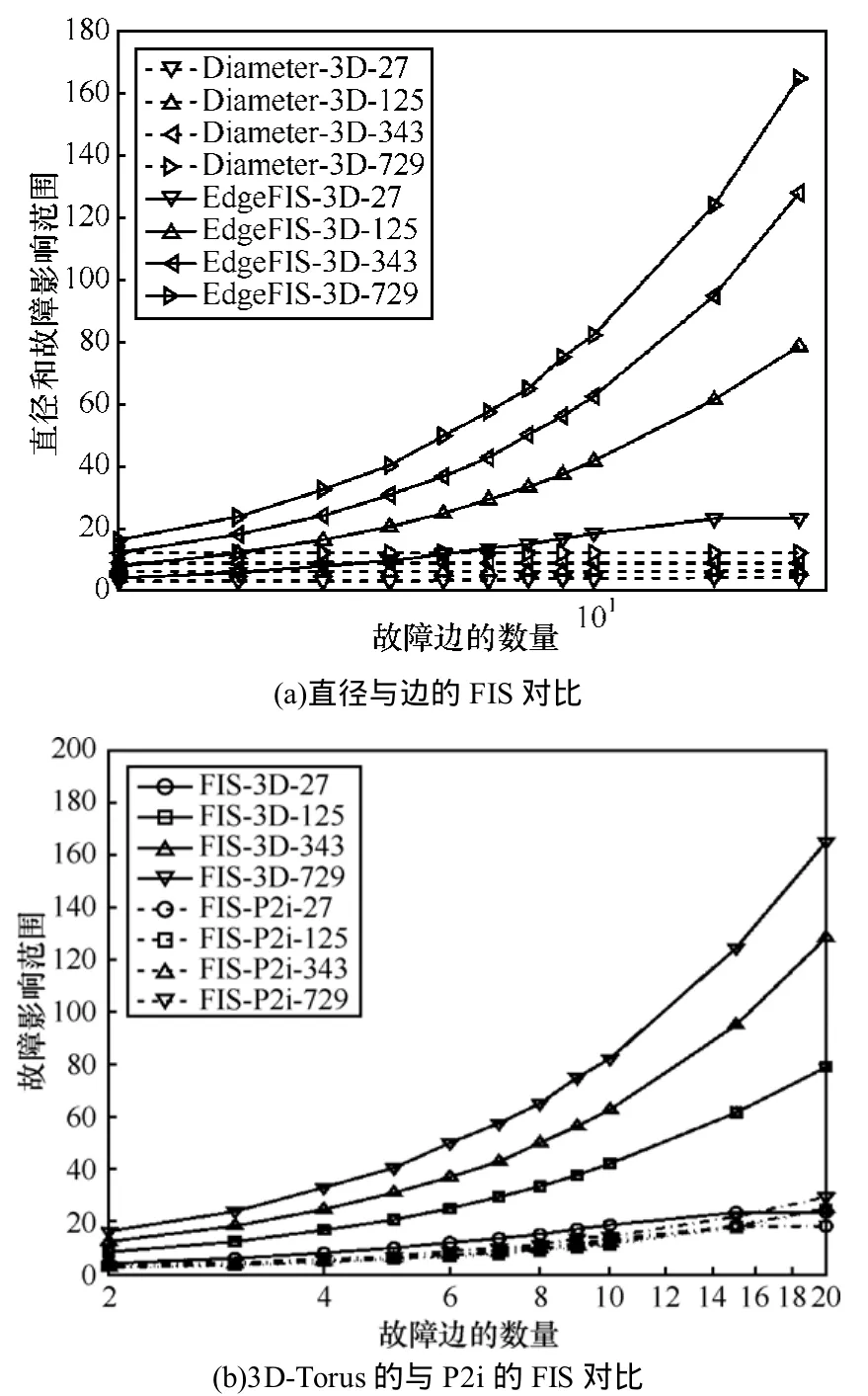
图5 直径与故障影响方法的敏感性对比以及不同网络的故障影响对比

图5(b)的实验（横坐标采用log坐标）采用与图5(a)相同的故障模型，以3D-Toru和P2i为例，对边故障影响范围进行对比。实验选择了27、125、343、729节点规模。图5(b)中各条虚线为P2i各个节点规模下的边故障影响属性。即使在发生故障的边从2逐渐增加到20后，P2i的边故障影响属性依然远优于相应规模的 3D-Torus。尤其值得注意的是，各个规模P2i的边故障影响属性(图5(b)中虚线)密集在一起。这说明即使节点规模扩大后，大规模P2i拥有与小规模P2i近似的边故障影响属性。从故障影响指标来看，P2i非常适宜进行规模扩展。

4.2 单故障实验结果及分析

单故障是指在某一时刻只有一个组件发生故障。这种故障模型在实际应用中较为常见，如对某个节点的维护和升级等情况。由于DN采用严格正交拓扑，点对称特性使得DN的单故障模型等同于随机单故障模型。在单故障模型下，故障影响评价方法包括单边故障影响范围和强度、单节点故障影响范围和强度等评价指标。本节实验在DN中选择了2D-Torus、3D-Torus和P2i 3种典型的网络，节点规模的最大值设为1 000。

实验结果如图 6所示，它们分别给出了不同DN的单边故障影响范围、单节点故障影响范围、单边故障影响强度、单节点故障影响强度随节点规模的变化情况。由图6(a)和图6(b)可以看出，在单随机故障模型下，P2i在大多数规模下拥有较3D-Torus更好的单边故障影响范围和单节点故障影响范围属性，且远优于2D-Torus。图6(b)说明，在随机单节点故障模型下，P2i拥有非常良好的故障影响范围属性。这意味着如果P2i规模增加或减少一个节点，对整个交换网络的影响较小，这种性质非常利于交换网络进行平滑的规模扩展。3DTorus的故障影响强度属性远优于 2D-Torus，且在节点规模小于500的情况下，拥有较P2i更好的单边故障影响强度属性和单节点故障影响强度属性。其原因可能主要源于P2i并非边对称结构，某些维度的边故障在特殊规模下对故障影响强度属性的影响更大。

4.3 相近连接网络的故障属性实验及分析

P2i和Torus连接和扩展方式不同。Torus的节点度固定，而P2i的节点度随着规模增大而渐增。通过4.1节和4.2节的实验可知两者的故障影响属性区别明显。P2i和 Hypercube具有相似的拓扑。它们具有近似的直径和节点度并且节点度都会随着规模而变化。本节实验以这2种相近连接网络为例，在随机故障模型下，使用故障影响强度指标FII对这对相似交换网络进行顽健性评价及对比。

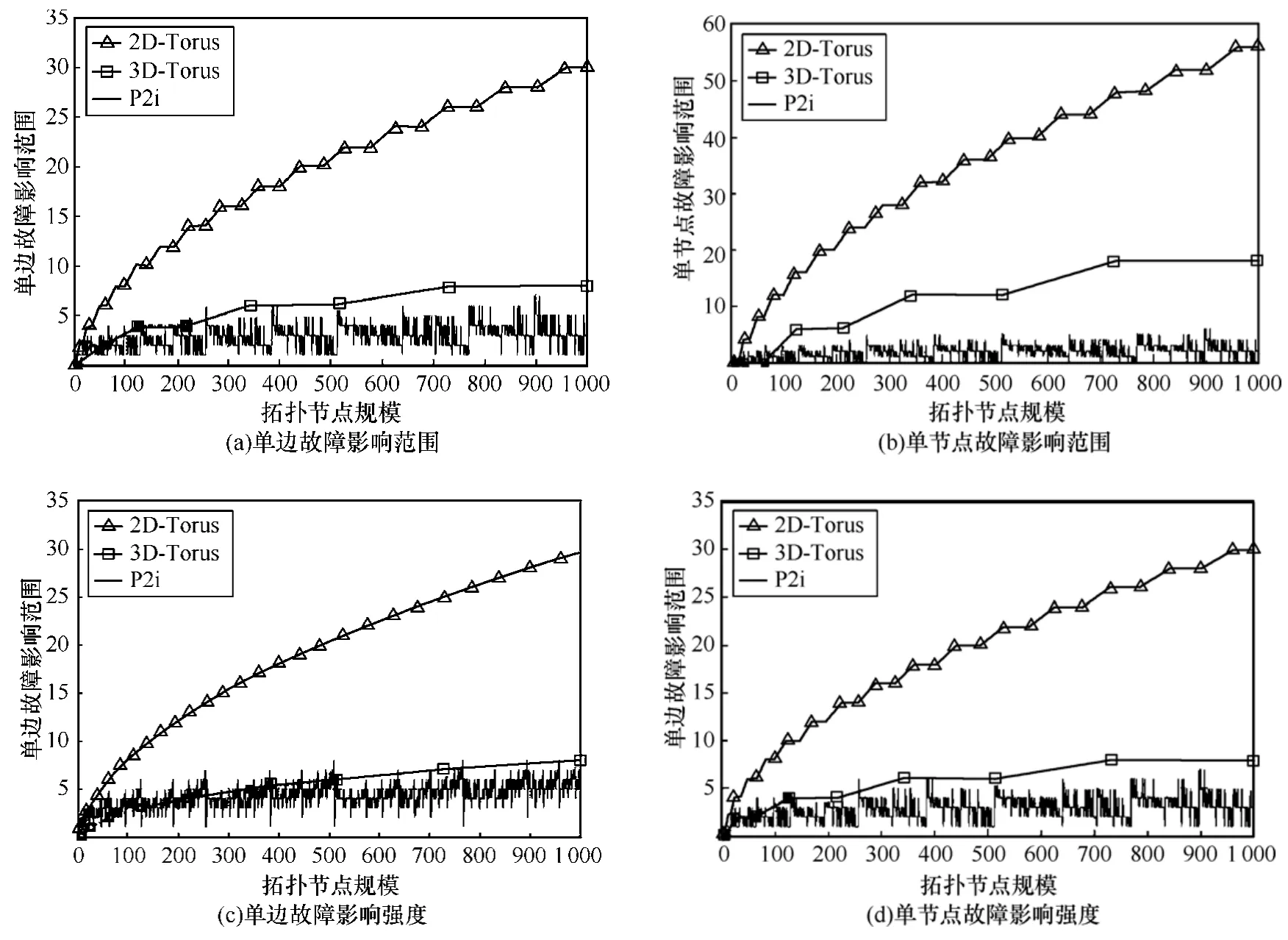
图6 在单节点和单边故障下的不同网络的故障影响属性对比

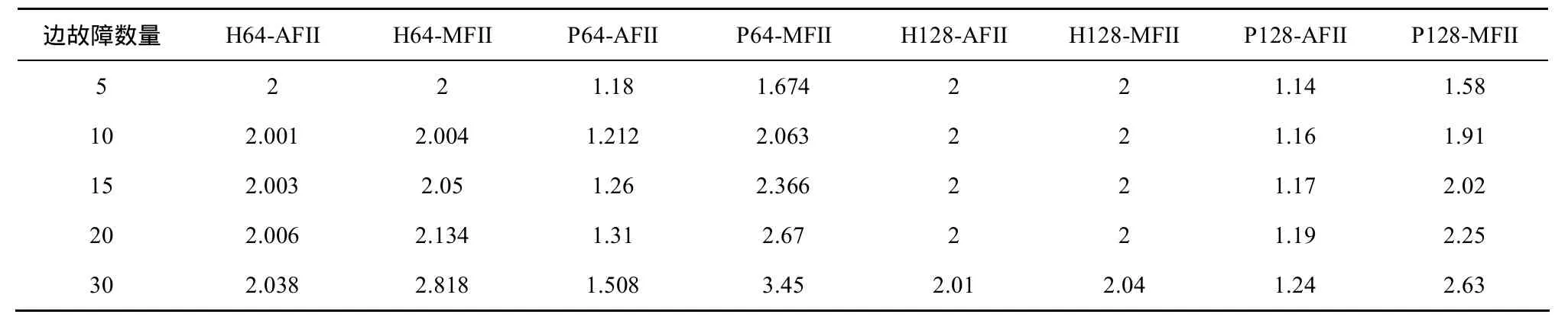
表2 P2i和Hypercube的平均边故障影响（AFII）和最大的边故障影响（MFII）比较

表3 P2i和Hypercube的平均节点故障影响（AFII）和最大的节点故障影响（MFII）比较

表2和表3是在随机边故障和随机节点故障模型下，64节点和128节点规模的P2i和Hypercube的FII属性。FII_E和FII_V分别表示发生故障的边和节点的个数。在随机故障模型下，FII的最大值和平均值分别记为 MFII、AFII。例如，64节点Hypercube的 MFII和 AFII分别记为 H64-MFII和H64-AFII。类似地，64节点 P2i的相关参数记为P64-AFII和P64-AFII。从表2和表3中的数据可以得出，P2i的 AFII属性优于 Hypercube，而 MFII属性较Hypercube差。这种差别可能缘于P2i边的不对称特性。P2i各维度的边跨度不同，0维边故障的影响强度高于其他维度的边。如果采用节点度和拓扑直径的概念，则无法对P2i和Hypercube的顽健性进行区分。而表2和表3的实验结果则表明，故障影响指标可以有效评价P2i和Hypercube的顽健性的区别。

5 结束语

可扩展交换网络的顽健性评价是可扩展路由器研究中的一个重要问题。基于DN的严格正交网络具备良好的扩展性并被广泛应用到可扩展交换网络的设计中。在随机故障模型下，现有顽健性评价方法不能有效地对DN顽健性进行评价。本文总结了基于DN的可扩展交换网络的拓扑特征，将图论中的顽健性评价方法引入可扩展交换网络的顽健性评价方法中，提出了基于故障影响的顽健性评价方法。这种方法包括2种评价指标，即故障影响范围和故障影响强度。实验和分析表明，在随机故障模型下，基于故障影响的顽健性评价方法可以有效地对DN的顽健性进行评价，并可以对相似拓扑的顽健性进行区分。

[1] LIU Z, ZHANG X, ZHAO Y,et al. An asymptotically minimal node-degree topology for load-balanced architectures[A]. Proc of the IEEE GLOBECOM 2008[C]. New Orleans: IEEE, 2008. 1-6.

[2] TSE H. Switch fabric design for high performance IP routers: a survey[J]. Journal of Systems Architecture, 2004, 51(10):571-601.

[3] KESLASSY I, CHUANG S, YU K,et al. Scaling internet routers using optics[A]. Proc of the 2003 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications[C]. Karlsruhe, Germany, ACM, 2003. 189-200.

[4] SUDAN R, MUKAI W. Introduction to the Cisco CRS-1 Carrier Routing System[R]. Cisco Systems California: Cisco Inc, Jan 1994.

[5] DALLY W. Performance analysis ofk-aryn-cube interconnection networks[J]. IEEE Transactions on Computer, 1990, (39): 775-785.

[6] DALLY W. Scalable Switching Fabrics for Internet Routers[R]. Computer Systems Lab, Stanford University: Stanford University and Avici Inc, 1999.

[7] ZHAO Y, YUE Z, WU J. Research on next-generation scalable Routers implemented with H-Torus topology[J]. Journal of Computer Science and Technol, 2008, 23: 684-693.

[8] DUATO J, YALAMANCHILI S, Ni M. Interconnection Networks:An Engineering Approach[M]. San Francisco, USA: Morgan Kaufmann, 2003.

[9] BRANDES U, ERLEBACH T. Network Analysis: Methodological Foundations[M]. New York, USA: Springer-Verlag, 2005.

[10] DALLY W, TOWLES B. Principles and Practices of Interconnection Networks[M]. San Francisco, USA: Morgan Kaufmann, 2003.

[11] KRISHNAMOORTHY V, THULASIRAMAN K, SWAMY M N S.Incremental distance and diameter sequences of a graph: new measures of network performance[J]. IEEE Trans Computer, 1990, 39: 230-237.

[12] GARTNER F C. Fundamentals of fault-tolerant distributed computing in asynchronous environments[J]. ACM Computer Survey, 1999, 31: 1-26.

[13] KOREN I, KRISHNA M. Fault Tolerant Systems[M]. San Francisco,USA: Morgan Kaufmann, 2007.

[14] ZHANG Z P. Fault Tolerant Routing Algorithms of Regular Networks and Reliable Multicast[D]. Changsha: Central South University, 2005.

[15] CHENG X, IBE O C. Reliability of a class of multistage interconnection networks[J]. IEEE Trans Parallel Distribute System, 1992, 3:241-246.

[16] BOESCH F, THOMAS R. On graphs of invulnerable communication nets[J]. IEEE Transactions on Circuits Theory, 1970, 17: 183-192.

[17] TANGMUNARUNKIT H, GOVINDAN R, JAMIN S,et al. Network topologies, power laws, and hierarchy[J]. ACM Sigcomm Computer Communication Review, 2002, 32: 76-76.

[18] BOESCH F T, HARARY F, KABELL J. Graphs as models of communication network vulnerability: connectivity and persistence[J].Networks, 1981, (11): 57-63.

[19] ZHANG X P, LIU Z H, ZHAO Y J,et al. Scalable router[J]. Journal of Software, 2008, 19(6): 1452-1464.