新型轮轨关系试验台研究

汪登荣，倪文波，王雪梅，李 芾

（西南交通大学 机械工程学院，四川成都610031）

轮轨磨耗是铁路运输中一直存在的一个重要问题，尤其随着重载、高速列车的发展，更加剧了轮轨的磨耗。轮轨的过度磨耗，一方面需要更换钢轨，旋修车轮等维护措施，增加了铁路的运输成本，另一方面给铁路运输带来安全隐患。而轮轨磨耗是复杂的摩擦学问题，很难通过理论计算来模拟和评估其过程特性，需要进行大量的试验研究。轮轨磨耗试验可以通过实际线路试验和试验台试验来完成，但实际线路试验，成本昂贵，周期长，而且不易控制各影响因素的单独作用。通过试验台试验不仅经济快捷，而且可以模拟各因素单独作用下对轮轨磨耗的影响，并且可以达到实际线路试验达不到的极限工况，所以通过试验台试验能够更好的进行轮轨磨耗的研究。

图1 轮—轮形式的轮轨关系作用试验台

图1是最为常见的轮轨作用试验台。这种类型的试验台采用一个按照一定比例制造的车轮来模拟实际的车轮，采用一个轨道轮来模拟轨道。轨道轮和车轮由各自的驱动电机来独立驱动旋转，从而模拟出纯滚动，以及不同蠕滑率时的工况。同时，通过作动器对车轮施加横向和垂向载荷，来模拟实际的列车运行时的轮轨间的各种工况。

这种类型的试验台具有控制简单、试验速度高的优点，可通过两个轮子的相互配合完成各种工况模拟，在国内外得到广泛的应用。1980年日本前川试验机研制所，研制成功轮轨实物环形疲劳试验台［1］，1981年在美国伊利诺斯理工学院就建有当时世界上先进的轮轨磨耗试验机－IIT－GMEMD［2］，2005年在德国联邦铁道研究中心，已具有速度能达到300km／h的轮轨作用试验台［3］。国内，1986年西南交通大学王夏秋教授在IITGMEMD技术基础上，研制成功我国第一台JD1型轮轨磨耗试验机，2008年建成更新为JD2型轮轨磨耗试验机，该试验机主要模拟高速工况下轮轨关系行为，最高模拟速度400km／h。2010年4月中国铁道科学院与德国RANK公司签订了最高速度500km／h的比例为1∶1的高速轮轨关系试验台的订购协议［4］。

上述各种轮轨试验台都能较好的进行各种工况下的轮轨模拟试验，然而，它们都基于轮—轮接触，在轮轨模拟试验中存在一定的近似，主要有以下几点［7］：

（1）轮轨接触关系

当存在一定的摇头角时，与实际的轮轨接触在接触点提前量上有相当差异；

（2）摇头重力力矩

由于两种工况下，重力力矩形成的原因不同，轮—轮接触的摇头重力力矩要远大于轮轨工况，大约是轮轨工况的15～20倍；

（3）接触斑特性

由于轮—轮接触中轨道轮的半径远小于实际轨道的半径，所以，轮—轮接触的接触斑形状与轮轨接触的形状存在差异，轮—轮接触的接触斑面积要小于轮轨接触。

综上所述，尽管采用轮—轮接触能够较好的模拟出轮轨磨耗情况，但是，由于轮—轮接触与轮轨接触仍然存在差异，试验结果和实际情况仍有一定差距。如果能够在试验室建立真正基于轮轨接触形式的试验台，试验结果将更接近实际情况。基于此，本文提出一种基于轮轨接触方式的新型轮轨关系试验台。

1 试验台传动机构方案

由于在试验室内轨道不可能无限长，采用轮轨接触方案时，需要采用一种往复运动机构，通过带动轨道来回运动来模拟轨道相对车辆运动。往复传动机构的选择与设计，对于试验台的性能至关重要。传统可实现往复运动的机构有曲柄滑块机构、齿轮齿条机构、液压缸往复运动机构等。2005年德国联邦铁道研究中心在对道岔进行试验时的试验台采用了曲柄滑块机构传动方案［3］，其机构运动简图如图2所示。

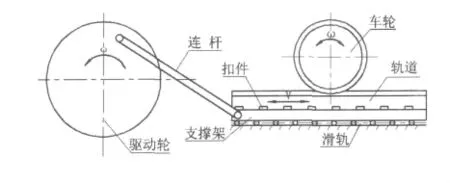
图2 采用曲柄滑块机构方案的机构运动简图

被试验道岔安装在一个能够往复运动的支承架上，支承架（即滑块）由曲柄机构驱动，滑块与地面间采用滑动导轨连接。轮对或转向架直接安放在道岔上，其上可通过龙门架和加载油缸模拟车辆对道岔的作用。由曲柄滑块机构运动特性可知，滑块在整个运动过程中，都在做非匀速运动（见图4曲线2），与实际的列车行驶状况不同。轨道行程增加就意味着增加主动轮半径，因此，轨道行程不可能足够长；对于齿轮齿条机构，由于需要齿轮的不断换向，对机械机构和电气系统都存在冲击；液压缸往复运动机构同样存在行程不易增长；尽管可以采用液压马达带动齿轮齿条往复运动，仍需要考虑不断改变液压油流向等问题。考虑到轮轨磨耗试验有一个长期的试验过程，其试验台必须能够长时间工作，因此本文采用一种新型的往复直线运动机构——行星齿环滑块机构来实现往复运动，其换向通过行星机构完成，电机无需换向控制，往复过程速度基本保持一致，利于实现长时间运行工作。其机构运动简图如图3所示。

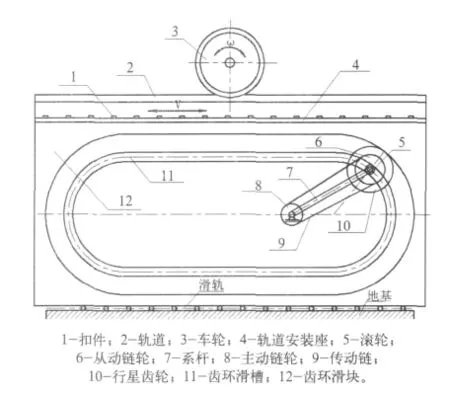
图3 行星齿环滑块机构运动简图

电机通过连轴器、减速箱等（此处省略未画）将动力传递给主动链轮。主动链轮轴线与系杆轴线重合，并且与固定在机架上的支座铰接，两者可以独立旋转。行星齿轮与从动链轮通过花键轴安装在同一轴上，该轴与系杆铰接，轴的一端安装有滚轮，滚轮嵌入在齿环的凹槽中。主动链轮通过传动链带动从动链轮和行星齿轮一起旋转。齿环滑块通过带有滚轮的滑轨与地基上的导轨接触，齿环内表面与行星齿轮啮合处附有齿轮齿廓。通过行星齿轮与齿环滑块的齿轮齿廓啮合以及齿环凹槽对滚轮的约束作用，可以带动齿环滑块以较低摩擦系数往复直线运动。

当主动链轮逆时针旋转，在如图3所示位置时，行星齿轮与齿环滑块两端环形部分齿轮齿廓啮合，同时行星轮轴带动滚轮沿圆形凹槽运动，从而带动系杆顺时针旋转。此时形成非固定轴齿轮啮合。当滚轮与齿环滑槽直线部分接触时，受凹槽约束，系杆不再旋转，行星齿轮与齿环下端内表面的直线部分齿廓啮合，此时，形成定轴齿轮齿条啮合，从而齿环滑块匀速向右运动，以此类推。当行星齿轮与左边环形面齿廓啮合时，形成非定轴传动，系杆逆时针转动，当滚轮与齿环滑块上端齿环滑槽接触时，形成定轴齿轮齿条啮合，齿环向左匀速运动。从而实现齿环匀速直线往复运动。通过改变齿环滑块直线部分的长度，可以改变直线往复运动的行程，改变电机的转速，可以改变往复运动的速度，而且不需要改变电机的转向就可以实现机构的变向运动。

图4 行星齿环滑块机构与曲柄滑块机构中滑块运动速度曲线对比

图4是行星齿环滑块机构与曲柄滑块机构的滑块运动速度曲线对比，曲线1是行星齿环滑块机构中滑块的速度曲线，曲线2是曲柄滑块机构中滑块的速度曲线。图中曲柄滑块机构中曲柄长400mm，连杆长1 200 mm，偏距为100mm，曲柄旋转角速度为5rad／s，齿环滑块机构的尺寸参数和下文数学模型参数相同。从图中可知，在工作过程中曲柄滑块机构的滑块一直做非匀速运动，而对于行星齿环滑块机构，除了换向过程，其滑块均可保持速度一致。

齿环滑块上部可安装被测试对象。例如通过扣件安装有两根实际的钢轨，轮对或转向架通过龙门架和作动器固定装置，安放在钢轨上，通过滑块带动轨道往复运动，从而带动轮对转动。通过安装两端不同高度的钢轨，来模拟实际的曲线超高，或安装道岔，即可模拟出列车过道岔的运行工况下轮轨的磨耗情况等。轮对或转向架通过加载作动器装置施加不同的垂向、横向载荷，来模拟列车实际运行中的车辆对线路的作用。

采用该试验台，通过在钢轨上贴应变片，即可测出不同工况下轮轨作用力，对研究轮轨作用力、轮轨磨耗、进一步开发低动力作用转向架、以及线路道岔结构有十分重要的意义。

2 齿环滑块机构运动数学模型建立

以齿环滑块的速度为例，建立齿环滑块机构的运动数学模型。当行星齿轮与齿环滑块右段圆弧段齿轮齿廓啮合时，运动简图及机构位置尺寸关系如图5所示。

图5 齿环滑块机构运动简图以及位置尺寸关系

O点为系杆和主动链轮的旋转中心，O1点为齿环端部圆弧的圆心，O2点为行星齿轮的转动中心，根据齿轮啮合定律，行星齿轮与齿环啮合点位于O1点和O2点连线的延长线上，啮合点在延长线与齿环的交点。L是系杆长度，α为系杆和水平线的夹角，β为O1和O2连线与水平线的夹角，R为齿环端部圆弧的半径，r为行星齿轮半径，ve为O2点的运动线速度，vm为行星齿轮转动线速度，va为齿环滑块直线运动速度。

选择O2为运动基点，O2点的速度ve为牵连速度，啮合点处行星齿轮旋转线速度ve为相对速度，va为啮合点处的绝对速度，设水平向右为X轴正方向，竖直向上为Y轴正方向，按照右手法则确定Z轴，从而建立绝对运动坐标系。根据刚体平面运动速度合成定律：

其中va、ve、vm分别表示对应的速度矢量。

将速度分别投影到X轴和Y轴上，由于在竖直方向上速度为0，建立平衡方程：

在X轴方向上：

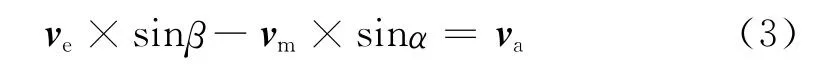
通过已知的几何位置关系，确定角度α和β关系：

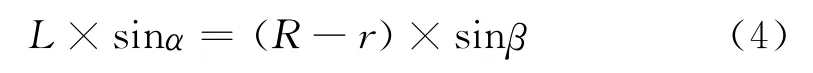
则：

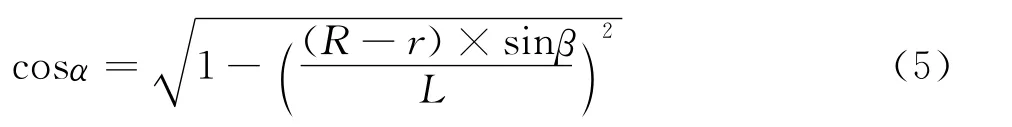
vm可以根据电机转速和各级传动的比例算出，将α与β的角度关系带入式（2）和式（3）中可得出滑块的绝对速度va和角度β以及行星齿轮转动线速度vm的对应关系如下：

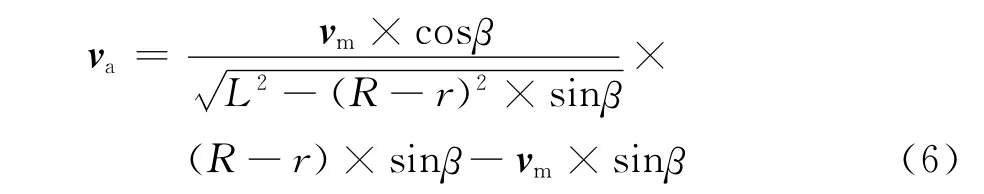
当行星齿轮与上下表面直线段齿轮齿廓啮合时，机构的运动为定轴齿轮齿条传动，齿环的速度va＝vm，即齿环的运动速度与行星齿轮的切向线速度相等。

当行星齿轮与齿环左端圆弧段齿轮齿廓啮合时，与行星齿轮与齿环右段啮合模型推导过程相似，可得到此时滑块的速度为：

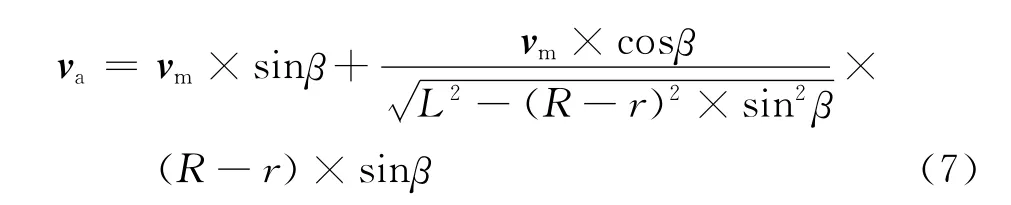
根据实际所需机构的大小，初步设定系杆长度L＝1 400mm，齿环滑块两端圆弧段齿轮齿廓分度圆半径R＝750mm，行星齿轮分度圆半径r＝100mm，行星齿轮分度圆上旋转切向线速度设定vm＝2 000mm／s。在MATLAB中绘制行星齿轮与齿环滑块左右两端圆弧段齿轮齿廓啮合时，以β为自变量，β的变化范围均为［pi／2，－pi／2］，va为函数值的关系曲线，如图6所示。

3 基于ADAMS的行星齿环滑块机构运动学仿真

通过Solidworks建立虚拟样机所需要的简化模型，再导入到ADAMS中，完成试验台传动机构的运动学仿真。

首先在Solidworks中建立机构简化模型，同时在Solidworks中设定各构件的材料和质量特性，以便下一步导入ADAMS中进行仿真分析，以行星齿轮为例，可以得到行星齿轮完整的质量特性，方便在ADAMS中计算仿真。

将Solidworks模型保存为Parasolid格式，通过该格式可以保存各零件的质量、转动惯量、质心位置、各零件的相对位置等重要信息，从而弥补ADAMS建立复杂模型困难的缺点，将模型导入到ADAMS中，设定各运动副，施加载荷和驱动，模型如图7所示。

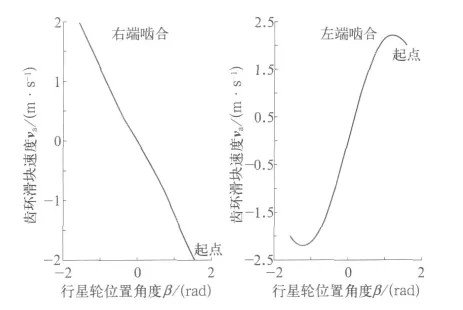
图6 行星齿轮与齿环滑块左右端圆弧段齿轮齿廓啮合时va－β曲线

图7 ADAMS中机构的运动模型

通过仿真计算得到齿环滑块质心的位移曲线，齿环滑块质心的速度曲线和系杆角速度曲线如图8所示。

结合理论计算，可以看出当行星齿轮与齿环滑块上下端齿条啮合时，齿环滑块匀速直线运动，连杆角速度为零，为定轴齿轮传动；当行星齿轮与齿环滑块右端圆弧段齿廓啮合时，齿环滑块的速度逐渐减小，系杆沿顺时针方向角速度逐渐增加；当系杆到达水平位置时，齿环滑块速度减小到零，而连杆此时角速度值达到最大；当系杆超过水平位置后，齿环滑块开始加速，连杆角速度开始减小，直到下一段齿条，齿环滑块速度增加到最大，系杆角速度减小到零；当行星齿轮与齿环滑块左端圆弧段齿廓啮合时，齿环滑块速度开始时略有增加，然后逐渐减小，系杆角速度一直增加，当系杆运动到水平位置，齿环滑块速度下降到零，系杆角速度增加到最大，当系杆超过水平位置，齿环滑块速度开始增加，快到达齿条啮合位置时，齿环滑块速度略有增加后，回复到匀速直线运动，而系杆角速度逐渐减小到零；到达齿轮齿条啮合位置后，系杆固定，形成定轴齿轮齿条传动，齿环滑块匀速返回。所以，在相应的齿条长度上可保证速度的一致。在换向过程中，加速度值最大约为±9.6m／s2，不会造成轮轨之间的滑行，符合实际运行工况。

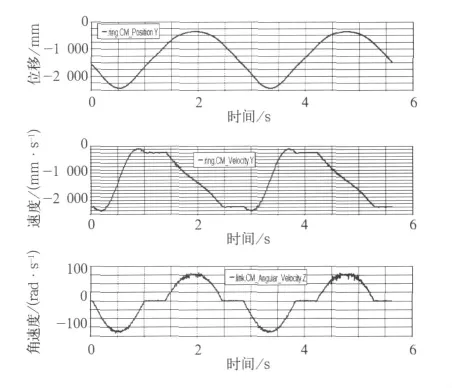
图8 齿环滑块质心位移、速度、系杆角速度仿真曲线

4 结束语

通过对行星齿环滑块机构理论计算和运动仿真，可以看出，该机构在电机转向不变的情况下，可实现齿环滑块的往复运动，同时在往复运动过程中可以实现匀速直线运动。尽管采用轮轨接触试验方式其线速度相对于轮—轮试验方式不高，但通过长期磨耗，其试验效果一致。将行星齿环滑块机构运用于轮轨关系试验台，不仅能够满足试验速度均匀，而且控制简单，还易实现长期工作。新型轮轨关系试验台的研究将可为铁路轮轨关系的研究提供重要的技术手段。

［1］王俊彪，马大伟，王成国.日本轮轨关系研究现状综述［J］.现代城市轨道交通，2009，（5）：5－8.

［2］S.KUMR（美），钱立新.轮轨接触参数的实验室模拟及轮轨冲角、蛇行运动、油水污染、真实接触面积对黏着—蠕滑特性的影响［J］.中国铁道科学，1984，5（1）：12－35.

［3］Detlev Ullrich，Andreas Zoll，Katrin Mädler（德）.Erprobung von Rad－und Schienentechnologien im Prüfstand und im Betriebsverbsversuch［J］.EI－Eisenbuhningenieur.2005，（8）：58－62.

［4］王成国.中国铁道科学研究院高速轮轨关系试验台建设取得进展［J］.中国铁道科学，2010，31（4）：68.

［5］向中凡，王进戈.行星齿环传动及其应用研究［J］.机械设计与研究，2007，23（4）：48－50.

［6］魏 华.行星齿环式无游梁抽油机的理论及设计［D］.成都：西华大学，2010.

［7］严隽耄，王开文，付茂海.机车车辆轮—轮与轮—轨接触关系的比较［J］.铁道学报，1994，16（增刊）：17－23.

［8］龚积球，谭立成，俞铁峰.轮轨磨损［M］.北京：中国铁道出版社，1997.

［9］李增刚.ADAMS入门详解与实例［M］.北京：国防工业出版社，2006.

［10］裴未迟，李耀刚，李运红.基于虚拟样机技术－ADAMS的冲击力模型［J］.河北理工大学学报（自然科学版），2008，30（4）：59－63.