基于显式有限元的高速列车吸能装置吸能原理研究＊

雷 成，肖守讷，罗世辉

（1 西南交通大学 牵引动力国家重点实验室，四川成都610031；2 郑州铁路职业技术学院 车辆工程学院，河南郑州450052）

虽然高速铁路是陆路交通中最安全的方式，但在实际的运营中，各种形式的人为错误和运行环境的突然变化却是不可避免的。由于高速列车乘客众多，速度较快，一旦发生意外事故，往往会带来严重的后果。而仅从主动安全防护方面不可能完全避免事故的发生。

因此，如何提高高速列车在碰撞事故中的被动安全性就成为一个不可忽视的重要问题。这样就需要设计专用吸能装置来吸收发生碰撞时列车的动能。因此吸能装置的设计是高速列车车体设计的关键环节。良好的吸能装置要求碰撞动能应尽可能不可逆地转换为变形能［1］。

本文提出一种新的碰撞能量耗散原理，即采用薄壁结构轴向切削吸能和轴向压缩吸能的组合作为新型吸能装置的吸能原理，从而吸收列车的动能，降低列车的减速度。由于薄壁金属构件被轴向切削时，吸能特性与刀具的前角、切屑的厚度及宽度等因素密切相关。因此本文将从这几个方面进行讨论，找出薄壁结构被轴向切削时的吸能规律。最后对本文提出的新的吸能原理与单一轴向压缩吸能的吸能原理的效果进行比较。

1 动态仿真显式有限元

薄壁结构切削过程是一个复杂的塑性变形过程，而且通常情况下是在高温、高速下产生的。当前对金属切削过程的研究工作已经深入到塑性力学、有限元法、位错理论以及断裂力学等范畴［2］。

随着计算机技术与有限元理论的发展，有限元技术已经成为研究金属切削过程及碰撞吸能过程的一个重要手段。显式时间积分特别适用于各种结构冲击动力学问题，如爆炸、碰撞和金属加工成型等高度非线性问题，它采用中心差分的时间积分，其基本特点是不形成总体刚度矩阵，弹性项放在内力中，避免了矩阵求逆，这对非线性分析很重要，无需检查收敛，是条件稳定的。金属切削过程具有动态性、大变形和高度非线性的特点，因此运用显式有限元程序对这一过程进行分析模拟非常适合［3］。本文采用通用的非线性显式动力分析程序LS－DYNA模拟吸能装置的吸能过程。

2 三维显式动力分析模型的建立

刀具采用硬质合金，其硬度、强度远远大于被切削工件材料，用刚体模拟。工件材料为4340钢，工件几何尺寸为100mm×6mm×10mm（长×高×宽），切削速度为10m／s，刀具后角5°，分别建立了刀具前角为20°，30°，40°和50°，切屑厚度分别为2，3，4mm，宽度为3，6mm的显式有限元模型。刀具前角20°，切屑厚度2mm，宽6mm时的切削过程三维有限元模型如图1所示。

图1 切削过程三维显式有限元模型

2.1 材料动态塑性本构模型

切削过程的实质是在一定的条件下，被切削材料在外力作用下，产生一个从弹性变形到塑性变形（滑移、孪生、晶界滑动、扩散性蠕动）再到断裂（切屑与工件分离）的过程。切削过程的等效应力—等效应变关系与应变、应变率、温度等多种因素有关［4］。选择合适的材料模型是准确模拟切削过程的关键。本文选用LS—DYNA材料库中的Johnson－Cook本构模型模拟被切削材料。模型使用下面的等效流动应力

式中T、Troom和Tmelt分别为变形温度、室温（一般取20°C）和材料熔点；A为材料的屈服应力（MPa）；B为应变硬化常数（MPa）；C，n，m为材料特性系数，可通过材料试验或切削试验方法获取。该本构关系未涉及材料变形的物理基础，方程中应变、应变率和温度对应力的影响是相互耦合的，且忽略了弹性变形。

2.2 切屑与工件的分离准则

薄壁金属结构的切削过程是一个使被切削工件材料不断产生分离的过程，切屑分离准则的确定对于成功实现切削过程模拟是至关重要的。到目前为止，在有限元模拟中切屑分离准则可以分为两种类型：几何准则和物理准则。几何准则主要基于刀尖与刀尖前单元节点的距离变化来判断分离与否。物理准则主要基于制定的一些物理量的值是否达到临界值而进行判断的。如几何分离准则［5］、应变能密度准则［6］、网格重划分准则［7］及断裂准则［8］等。

Johnson和Cook提出把应变率、应变、温度和压力都考虑进去的剪切失效准则。这个准则的特点是和实验相结合，因此比较可靠，该失效准则特别适用于金属高应变率变形，因此广泛应用于动态仿真数值模拟。

本文应用Johnson和Cook提出的材料失效准则并结合失效单元删除的方法实现切屑与工件的分离，切削过程中当达到切屑分离准则时，发生材料失效，失效单元自动从模型中删除，最终实现切屑的分离。

2.3 刀屑接触和摩擦模型

切削层材料与工件母材分离后形成切屑。建立模型时需要解决的关键问题是切屑与刀具的摩擦，由于实际切削过程中切屑与前刀面的接触分为两个区域，在黏接区域为内摩擦，在滑动区域为外摩擦。因此本文采用如下模型定义切屑与刀具的摩擦［9］。式中f为摩擦应力；σn为刀屑接触界面的正应力；μ为滑动摩擦区域的摩擦因数；υc为黏性摩擦因数，用于限制最大摩擦力，根据黏接摩擦的性质将其取为剪切屈服应力，即为接触材料屈服应力。

3 显式动力分析结果

采用上述有限元模型对4340钢的直角自由切削过程进行三维显式动力分析。随着刀具的切入，切削层材料与工件母体逐渐分离形成切屑。

3.1 切屑层材料的塑性流动

图2为刀具前角50°，切屑厚度2mm，宽3mm，0.002s时的最大剪应力（maximum shear stress）云图。可以看出，塑性流动在切屑起始弯曲的部分值最大，并且向切屑两边逐渐减小。

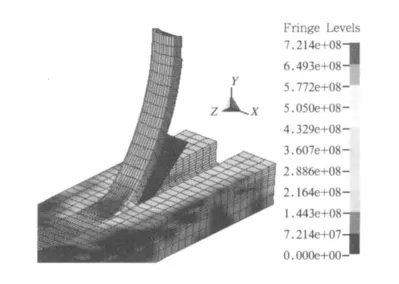
图2 切削过程中材料的塑性流动现象

3.2 刀具前角对切削吸能特性的影响

刀具前角不同，切屑厚度为2mm，宽6mm时，切削过程吸收的能量、界面力随时间的变化曲线分别如图3、图4所示。可以看出，相同条件下，切削过程中界面力和吸收的能量与刀具的前角成正比。

图3 刀具前角不同时的内能—时间历程图

3.3 切屑厚度、宽度对切削吸能特性的影响

刀具前角为50°，切屑厚度、宽度不同时，切削过程中吸收的能量、界面力随时间的变化曲线分别如图5、图6所示。从图中可以看出，切削过程中界面力、吸收的能量与切屑的厚度、宽度成正比，并且随着刀具的切入，界面力趋于稳定。

图4 刀具前角不同时的界面力—时间历程图

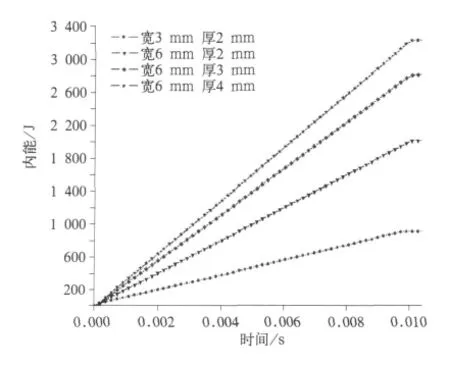
图5 切屑厚度、宽度不同时内能—时间历程图

图6 切屑厚度、宽度不同时界面力—时间历程图

前角50°，切屑厚度、宽度不同时，切削过程中的吸能、界面力稳定值大小如表1所示。

刀具前角50°，切屑厚度相同时，切削吸能结果与切屑宽度的关系如表2所示。

从表2可以看出，刀具前角、切屑厚度相同时，切削吸能比、界面力稳定值比约等于切屑宽度比。

刀具前角50°，切屑宽度相同时，切削吸能结果与切屑厚度的关系如表3所示。

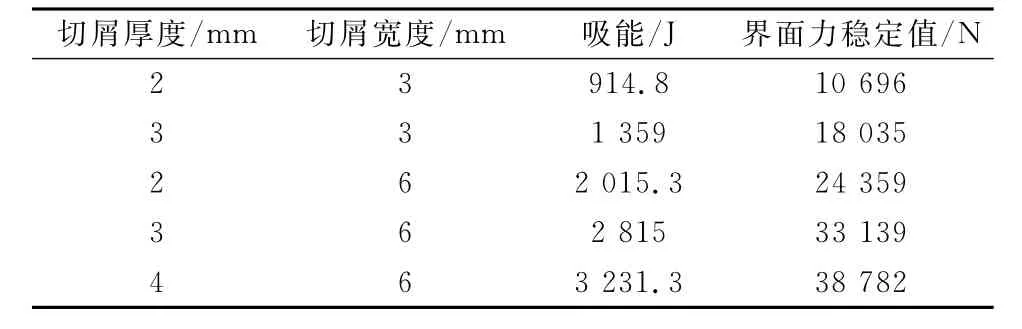
表1 切削过程中的吸能、界面力稳定值大小

表2 切削吸能结果与切屑宽度的关系

表3 切削吸能结果与切屑厚度的关系

从表3可以看出，刀具前角、切屑宽度相同时，切削吸能比、界面力稳定值比约等于切屑厚度比。

4 新型吸能装置吸能原理设计

本文提出采用轴向切削吸能与轴向压缩吸能组合作为吸能装置的吸能原理，如图7所示。刀具和刚性墙固定，两者间相距一定的距离，薄壁圆管以恒定的速度从右向左运动，首先与刀具接触，并产生切屑，吸收能量；接着薄壁圆管已被切削的部分与刚性墙接触，产生塑性变形，吸收能量。

采用该原理设计的吸能装置吸收的能量，可以近似等效为等壁厚薄壁圆管轴向切削时吸收的能量与不等壁厚薄壁圆管轴向压缩时吸收的能量之和。

图7 新型吸能装置原理图

5 吸能效果比较

根据以上分析，对第4节中设计的吸能原理与单一轴向压缩吸能的吸能效果进行对比。等壁厚薄壁圆管的壁厚为6mm，不等壁厚薄壁圆管的壁厚共两种，较大处6mm，较小处3mm，并且壁厚较小处的弧长为6 mm。两种薄壁圆管的长度都是100mm，内径都是100 mm。两种圆管的横截面如图8所示，左边为不等壁厚圆管，右边为等壁厚圆管。

图8 薄壁圆管横截面图

切屑的厚度为3mm，宽度为6mm，刀具前角20°，由3.2节可知，一个刀具以10m／s的恒定速度切削时吸收的能量为3 287J。相同条件下，8个刀具同时切削，吸收的能量则为3 287×8＝26 296J。

采用第2节中相同的材料模型、单元类型、初始条件等建立不等壁厚、等壁厚薄壁圆管轴向压缩的有限元模型，刚性墙以10m／s的恒定速度从右向左运动，薄壁圆管底面固定。有限元模型如图9所示，左边为不等壁厚圆管，右边为等壁厚圆管。

经计算可得，在冲程效率为70%的情况下，不等壁厚圆管吸收91 732J的能量，等壁厚圆管吸收97 817J的能量。

根据第4节提出的近似等效，采用新的吸能原理，相同条件下，吸收的能量可以等效为：26 296＋91 732＝118 028J。两种吸能原理的吸能效果比较如表4所示。

图9 薄壁圆管压缩有限元模型

表4 两种吸能原理吸能效果的比较

由表4可以看出，新型吸能原理的吸能效果较好。

因此，轴向切削吸能和轴向压缩吸能的组合是一种较好的碰撞能量耗散模式，有必要进行进一步的研究。相信通过对刀具前角、刀具数量、切屑厚度、宽度以及吸能装置结构等的优化设计，采用该吸能原理设计的吸能装置吸能效果将会进一步提升。

6 结论

综合以上分析，可以得出以下结论：

（1）轴向切削薄壁结构时的吸能特性与刀具的数量、切屑的厚度和宽度等密切相关。吸收的能量和界面力的大小与刀具的数量成正比；相同条件下，切屑厚度不同时，切削过程的吸能比、界面力稳定值比约等于切屑厚度比；切屑宽度不同时，切削过程的吸能比、界面力稳定值比约等于切屑宽度比。

（2）通过仿真分析，证明了轴向切削吸能和轴向压缩吸能组合具有良好的吸能效果，是一种理想的碰撞能量耗散模式，可以作为高效吸能装置使用，并有必要进行进一步的研究。

［1］胡小伟.高速动力车碰撞模拟研究［D］.成都：西南交通大学，2001.

［2］杨晓琦，韩凤起.基于正应力摩擦模型的金属切削有限元仿真［J］.电子机械工程，2008，24（4）：48－50.

［3］Soo SL，Aspinwall D K，Dewes R C.3DFE modeling of the cutting of Inconel 718［J］.Journal of Materials Processing Technology，2004，105：116－123.

［4］刘战强，吴继华.金属切削变形本构方程的研究［J］.工具技术，2008，42（3）：1.

［5］Ship peng Lo.An analysis of cutting under different rake angles using the finite element method.Journal of Material Processing Technology，2002，105：143－151.

［6］Zone ching Lin，Ship peng Lo.2－D discontinuous chip cutting model by using strain energy density theory and elastic－plastic finite element method.International Journal of Mechanical Sciences，2001，43：381－398.

［7］A G Mamalis，A S Branis.Modeling of precision hard cutting using implicit finite element methods.Journal of Materials Processing Technology，2002，123：464－475.

［8］Ceretti E，Fallbohmer p，Wu W T et al.Application of 2DFEM to chip formation in orthogonal cutting.Journal of Materials Processing Technology，1996，59：169－180.

［9］郭建英，吕明.金属切削过程的三维显式动力分析［J］.机械强度，2009，31（1）：160－165.