一种轨道车辆用带箍结构空气弹簧的非线性有限元分析
莫荣利,陈文海,唐应时,黄友剑,陈灿辉
(1 株洲时代新材料科技股份有限公司,湖南株洲412007;2 湖南大学 机械与运载工程学院,湖南长沙411000)
对车辆用空气弹簧弹性特性的研究目前主要还是采用理论分析和试验测定的方法,用有限元法分析空气弹簧特性还处在探索阶段。理论分析方法可以用解析法或图解法对形状简单的空气弹簧计算出近似解。
对于形状复杂的空气弹簧,图解法则计算过于繁琐、精度不高、可操作性差,对实际工程应用的指导意义不大[1]。且其气囊本体的刚度还需要通过试验来确定,但试验方法受试验条件和试验环境限制,并且试样试制开发周期长,研制费用也很高。
随着计算机技术的发展和工程力学有限元分析理论的不断完善,应用数值计算方法来分析、研究空气弹簧系统的特性可以避免解析和图解方法计算中的假设条件,并且可以比较真实地模拟空气弹簧。
1 非线性及分析方法
1.1 非线性问题
结构的非线性问题是指结构的刚度随其变形而改变的分析问题。在非线性分析中,结构的刚度矩阵在分析过程中必须进行许多次的更新、求逆,这使得非线性分析求解比线性分析更加耗时,计算费用也更多[2-3]。
空气弹簧结构分析涉及了气囊和辅助弹簧材料的非线性、大变形带来的几何非线性以及气囊与上盖板和辅助弹簧接触非线性。
1.2 非线性问题分析的主要方法
(1)弧长法
弧长法是用于求解非线性负刚度问题最为有效的方法。弧长法的适用性很强,收敛性和鲁棒性明显好于其他处理负刚度问题的方法。但是该方法计算量相当大。
(2)载荷增量法
载荷增量法具有普遍的适用性,除了应用于负刚度问题外,它能够适用于所有的非线性问题,只要控制好载荷的增量水平就可以达到收敛的目的。
2 带箍结构空气弹簧有限元模型的建立
2.1 带箍结构空气弹簧的材料本构模型
如图1所示,橡胶-帘线复合材料实质上是由作为增强相的帘线在气囊基体相橡胶中排列成的刚柔相辅的复合材料,呈现明显的各向异性和非线性特性[3]。

图1 单层橡胶—帘线复合材料的微观结构
(1)气囊橡胶材料的本构模型
空气弹簧系统在运动过程中,橡胶气囊产生较大的挠曲变形,其橡胶材料表现出高度的非线性。其简单的超弹性模型为 Mooney-Rivlin形式[3]。
(2)辅助弹簧橡胶材料的本构模型
空气弹簧辅助弹簧由橡胶层和金属板组成。辅助弹簧对空气弹簧系统横向性能影响很大,为了更加精确地对其进行模拟,对所用胶料配方试样进行了单轴拉伸试验、双轴拉伸试验和平面剪切试验。以上试验在美国AXLE公司完成,运用Odgen(N=4)本构模型进行拟合[4]。在本文的计算中辅助弹簧橡胶部分采用三维8节点实体单元C3D8RH。辅助弹簧钢板采用三维实体单元C3D8R。
(3)帘线层的结构及其非线性
帘线层是橡胶气囊的主要受力部件,由于帘线的拉伸模量不等,使得帘线层呈现出复杂的力学各向异性和非线性。帘线层的合理模拟是有限元分析结果正确与否的关键。橡胶—帘线纤维加强材料处于主流的方法是用重叠单元的方法,即在基体单元上叠加上重复的单元,如图2所示,共用相同的节点,基体单元和重叠单元分别定义橡胶和纤维的材料属性,这种重叠的单元称为加强筋单元。这种单元并没有增加节点数量,计算费用没有显著增加,此外,在应力后处理时还可以方便的得到橡胶和帘线中的应力状态[5]。分析中,气囊部分选择4节点壳单元(S4R),每个节点有6个自由度。
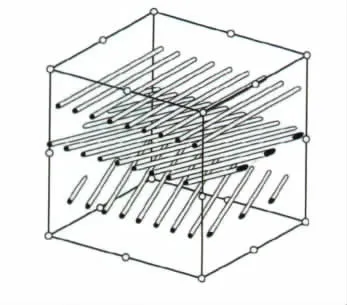
图2 加强筋单元模拟帘布层数
2.2 空气弹簧腔内气体
在进行空气弹簧弹性特性分析时,假设空气弹簧腔内的气体为理想气体,并且在工作过程中,气体的温度保持不变,即等温过程[6]。
采用两种气体单元F3D3和F3D4,应用ABAQUS中符合流体静力学条件的充腔气体单元模拟空气弹簧腔内气体。
2.3 气囊中间箍结构的处理
气囊中间箍结构如图3所示,中间箍在压出时,钢丝上就已附上了一层橡胶,实际上钢丝就是浸泡在橡胶中。中间箍橡胶与气囊外层橡胶是相同的材料,钢丝在气囊中主要受到拉伸作用,弯曲作用的影响可以忽略不计,同时考虑到三维实体单元可以在任何表面与其他单元连接起来,三维实体单元与气囊壳单元外表面共用单元节点,所以采用三维实体单元C3D8R来近拟模拟。
2.4 接触与约束
接触问题是一种高度非线性行为,接触过程通常是依赖于时间,并伴随着材料非线性和几何非线性的演化过程。特别是接触界面的区域和形状以及接触界面上运动学和动力学的状态也是事前未知的。就此特点决定了接触问题通常采用增量方法求解。本文采用罚函数法,其优点是不增加结构的自由度,而且使求解方程的系数矩阵保持正定。
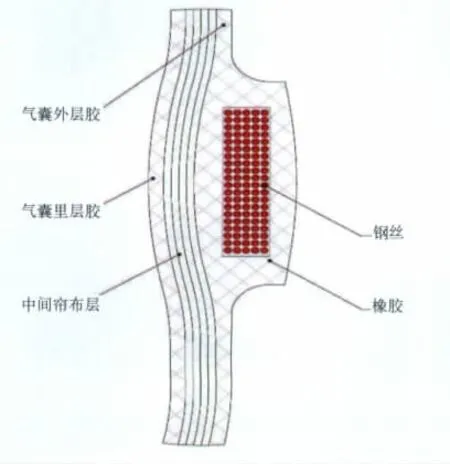
图3 气囊中间箍结构示意图
2.5 带箍结构空气弹簧计算模型
上盖板和辅助弹簧都各自定义一个参考点,位于空气弹簧对称轴与上盖板和辅助弹簧的交点上。在仿真计算中,对上盖板和辅助弹簧所施加的边界条件和约束条件可以直接定义到各自的参考点上。综上所述,建立的空气弹簧模型共有10 187个4节点四边形壳单元(S4R),4 382个三维4节点(F3D4)和168个三维3节点(F3D3)气体单元,39 120个三维8节点(C3D8RH)实体杂交单元,10 187个三维8节点(C3D8R)实体单元。此外,还定义了1个刚体来模拟上盖板。带箍结构空气弹簧有限元分析模型如图4所示。

图4 空气弹簧有限元分析模型
3 有限元分析结果
3.1 空气弹簧的垂向性能有限元分析
应用ABAQUS/Standard的求解模块,对车辆空载条件下的空气弹簧有限元模型垂向特性(位移—力)进行求解。图5和图6分别为空气弹簧压缩和拉伸到+35mm/-50mm时空气弹簧的应力云图。

图5 空气弹簧垂向拉伸50mm气囊应力云图

图6 空气弹簧垂向压缩35mm气囊应力云图
3.2 空气弹簧的横向性能有限元分析
由于橡胶气囊在径向具有一定的伸缩性,导致了在不同载荷条件下,橡胶气囊的横向特性也有相应的变化。应用ABAQUS/Standard的求解模块,对车辆空载条件下的空气弹簧有限元模型横向特性(位移—力)进行求解。图7为空气弹簧横向位移到60mm时空气弹簧的应力云图。

图7 空气弹簧横向位移60mm应力云图
3.3 有限元计算与试验结果的对比分析
为了验证本文所建立的空气弹簧有限元模型的正确性,运用国家认可实验室株洲电力机车研究所弹性元件检测中心的二维电子试验机对样品进行了空载条件下的垂向、横向特性试验,并将试验结果与有限元分析结果进行了对比,如表1、表2及图8、图9所示。
(1)垂向特性试验方法:在室温23±2℃下,在设计高度下,辅助气室:100dm3时,充气至内压0.4MPa,气压稳定后,以1mm/s的速度,分别沿垂向压缩方向施加0~+35mm和拉伸方向施加0~-50mm的位移,记录位移—载荷曲线。
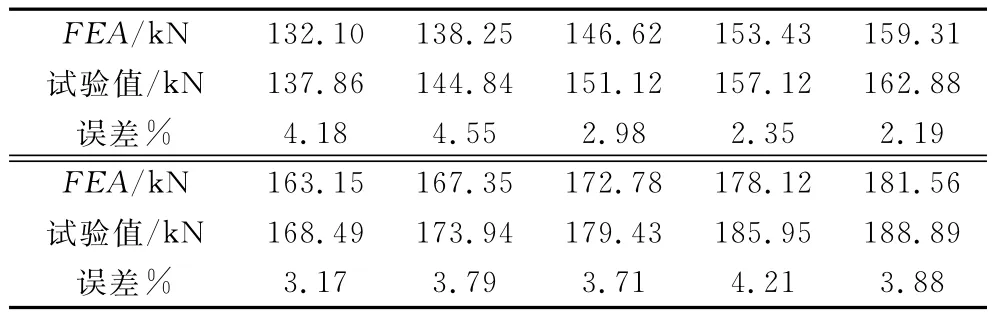
表1 垂向特性FEA与试验结果的比较
(2)横向特性试验方法:在室温23±2℃下,在设计高度下,辅助气室100dm3时,充气至内压0.4MPa,气压稳定后,以1mm/s的速度,沿垂向施加0~60mm的位移,记录位移—载荷曲线。

表2 横向特性FEA与试验结果的比较
从试验与有限元分析计算的结果对比来看,垂向误差为5%以下,横向误差为12%以下。可以得出有限元计算结果与试验结果是基本一致的,从而验证了本文所建立的带箍结构空气弹簧有限元模型是正确的。但总的说来,计算误差横向比垂向要大,尤其是在位移较大时。其主要原因是在分析建模时,对空气弹簧气囊上、下钢丝圈及帘布反包结构进行了简化,仅仅考虑了气囊参与变形较大的囊体部分。与此同时在横向位移较大时气囊与上盖板的接触效应更加显著,非线性更加明显,这样导致有限元分析的结果与实际试验结果偏小,并随着位移的增加,误差也随之增大。
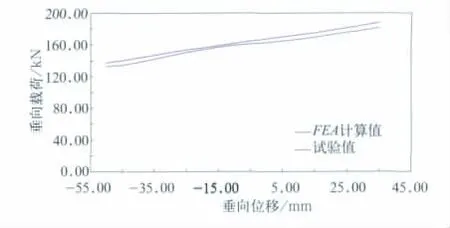
图8 空气弹簧垂向特性曲线

图9 空气弹簧横向特性曲线
4 带箍结构空气弹簧特性分析
4.1 附加气室容积对空气弹簧垂向性能的影响
分析结果表明:在不同载荷条件下,空气弹簧垂向刚度与附加气室容积变化呈非线性特性,随着附加气室容积的增大而逐渐减少,变化递度趋向于零,如图10所示。
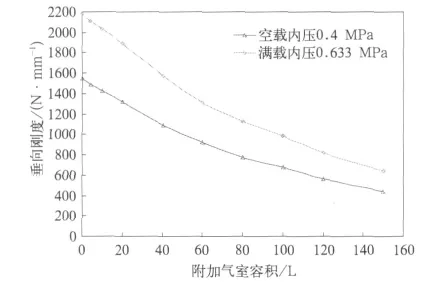
图10 空气弹簧垂向刚度与附加气室容积的关系
4.2 内压对空气弹簧承载能力的影响
通过分析计算得到空气弹簧刚体上盖板参考点处的反作用力计算数值,经过数据处理绘制出内压与载荷的关系曲线,如图11所示。从图中可以看出,空气弹簧的承载能力随着内压的增大而增大,接近线性关系。在不同安装高度下,空气弹簧内压与其承载能力变化小。
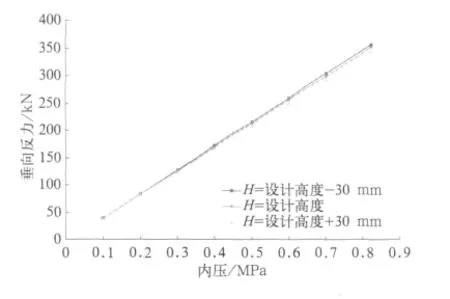
图11 空气弹簧垂向反力(承载能力)与内压的关系
4.3 帘线角度对空气弹簧性能的影响
4.3.1 不同帘线角度对空气弹簧垂向特性的影响
从图12中可以看出空气弹簧垂向刚度随着帘线角的增大而减小,但变化幅度不大。
4.3.2 不同帘线角度对空气弹簧横向特性的影响
从图13中可以看出空气弹簧横向刚度随着帘线角的增大而增加,但变化幅度不大,这与垂向性能变化刚好相反。
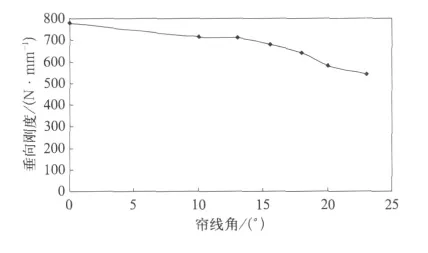
图12 空气弹簧垂向刚度与帘线角的关系

图13 空气弹簧横向刚度与帘线角的关系
4.4 帘布层数对空气弹簧性能的影响

表3 帘布层数与空气弹簧垂向和横向刚度的关系
由表3的结果可以看出空气弹簧的帘布层数越少,垂向和横向刚度越低,但垂向变化幅度不大而横向刚度变化幅度较大。
4.5 上盖板角度对空气弹簧性能的影响
4.5.1 不同上盖板角度对空气弹簧垂向特性的影响
从图14中可以看出空气弹簧垂向刚度随着帘线角的增大而略微增加,变化幅度不大。

图14 空气弹簧垂向刚度与上盖板角度的关系
4.5.2 不同上盖板角度对空气弹簧横向特性的影响
从图15中可以看出空气弹簧横向刚度随着帘线角的增大而增加,但变化幅度较垂向刚度大。
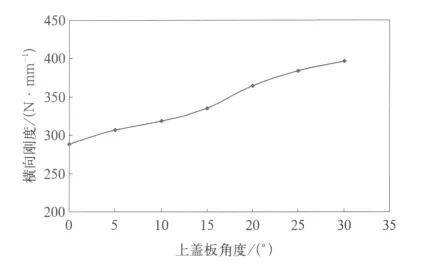
图15 空气弹簧横向刚度与上盖板角度的关系
4.6 辅助弹簧橡胶材料硬度对空气弹簧刚度性能的影响
4.6.1 橡胶材料硬度对空气弹簧垂向刚度的影响
从图16中可以看出,辅助弹簧橡胶材料硬度的变化对系统的垂向刚度影响甚微,而且没有简单的线性关系。但从图中还可以得出一个结论:空气弹簧的内压(载荷)越大,其垂向刚度也大,这与理论分析是完全一致的。

图16 空气弹簧垂向刚度与辅助弹簧胶料硬度的关系
4.6.2 橡胶材料硬度对空气弹簧横向刚度的影响
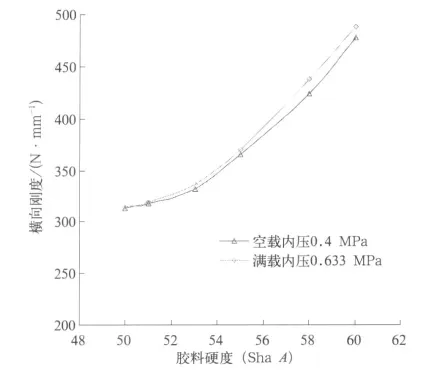
图17 横向刚度与辅助弹簧胶料硬度的关系
从图17中可以看出,辅助弹簧橡胶材料硬度的变化对系统的横向刚度影响非常大,而且非线性关系非常明显。从图中还可以看出,空气弹簧的内压(载荷)越大,其横向刚度却变化不大。
5 结论
(1)空气弹簧垂向性能分析与试验对比的误差小于5%;横向小于12%。研究表明所运用的计算方法是行之有效的,可以应用于类似空气弹簧的性能分析,并将为新型空气弹簧的设计、研制开发提供了一定的理论计算依据。
(2)分析表明空气弹簧的垂向刚度随着附加气室的容积增大而减小。但变化梯度趋于平缓。
(3)空气弹簧的承载能力随着内压的增大而增大,大致呈线性关系。
(4)帘线角度对垂向、横向性能的影响刚好相反,对刚度的影响幅度不大,因此不能寄希望通过改变帘线角度对空气弹簧性能进行大的调整。
(5)上盖板角度对横向性能影响较大,但垂向却变化不大。
(6)辅助弹簧的橡胶硬度对空气弹簧横向性能影响较大,但垂向却变化不大。
本文主要是对空气弹簧的静态特性进行研究的,空气弹簧的分析与研究还有许多工作要做。
(1)空气弹簧的结构模拟,在本文实际处理时局部做了一些简化,这对计算结果会产生一些误差。如要提高计算的精度,还需要对模型进行更为细致的处理。尤其是气囊与上盖板之间的接触、摩擦单元的处理。
(2)空气弹簧的使用过程实际是一个动态的过程,所以,空气弹簧动态的特性与静态的模拟特性存在一定的差别,在以后的研究中应当考虑进行动态分析。
[1]叶珍霞,朱海潮,鲁克明,等.囊式空气弹簧刚度特性的非线性有限元分析[J].振动与冲击,2006,25(4):94-97.
[2]G.R.liu S.S.Quek.有限元法实用教程[M].长沙:湖南大学出版社,2004.
[3]刘 展.ABAQUS 6.6基础教程与实例详解[M].北京:中国水利水电出版社,2008.
[4]TRAN HUU NAM,TRAN ICH THINH.Large deformation analysis of inflated air-spring made of rubber-textile cord composite[J].Structural Engineering and Mechanics,2006,24:31-50.
[5]任旭春.轮胎有限元分析及优化中的若干问题研究[D].北京:清华大学,2005:4-22.
[6]王成国,刘金朝.空气弹簧的数字设计[J].铁道机车车辆,2003,(增2):35-39.

