静止方柱和圆柱绕流的二维数值分析

毕继红 余化军 任洪鹏

（1.天津大学 建筑工程学院，天津 300072；2.滨海土木工程结构与安全教育部重点实验室（天津大学），天津 300072）

在一定的雷诺数范围内，粘性流体流经高层建筑物、桥塔、海上石油钻井平台、大跨度的悬索桥或斜拉桥、输电线等具有钝体截面形状的结构物时，会发生边界层的分离现象，进而对结构产生周期性的气动力作用，这就是所谓的绕流问题.绕流问题一直是众多学者研究的热点，现有的研究成果大都以圆柱为研究对象.史里希廷［1]依据实验结果绘制了圆柱绕流的斯托罗哈数St、阻力系数Cd随雷诺数（Re从1到107）的变化曲线，发现圆柱绕流的阻力系数值在Re＝5×105左右时突然由1.2下降到0.3，这种阻力值突然显著减小的现象被称为阻力危机现象.曹丰产、项海帆［2]用基于一般曲线坐标系和交错网格的差分法求解原始变量二维不可压缩粘性流体的N－S方程，计算了雷诺数Re从100到1×105范围内圆柱的非定常绕流，得到了涡脱频率f、阻力系数Cd，不足之处是在雷诺数较高时其阻力系数与实验结果偏差较大.詹昊等［3]利用Fluent数值模拟的方法对圆柱在不同雷诺数范围内绕流的气动力参数进行了系统的分析，研究了涡脱落规律，验证了圆柱绕流阻力危机的存在.

方形截面也是一种典型的钝体截面形式，现有文献一般是研究雷诺数较低时的情形，对于高雷诺数时的方柱绕流则甚少涉及.Davis and Moore［4]研究了不同纵横比矩形截面柱体的阻力以及尾流，但研究仅限于较低雷诺数下通过实验研究了不同截面纵横比的矩形截面柱体在Re＝70～20 000范围内斯托罗哈数St与雷诺数Re的关系，但没有涉及另一重要的参数Cd.Kim D H［6]等采用大涡模拟的方法研究了Re＝3 000时的方柱，比较了方柱位于固定的狭小通道中和位于无限区域中的情形，发现当柱体位于狭小通道中时，由于固壁边界的存在，阻力值有着明显的增大.

绕流中周期性的气动力作用有可能引起结构物的破坏，因此采用流体计算软件CFX进行数值模拟，系统研究方柱和圆柱的St、Cd随Re（从层流区到超临界区）的变化规律，比较方柱和圆柱的绕流参数，对于进一步认识绕流问题以及工程结构的设计具有重要意义.

1 控制方程

在直角坐标系下，对二维不可压缩粘性流体，其运动规律用纳维斯－斯托克斯方程（N－S方程）［7]描述：

式中，U、V为流体沿x、y向的分速度；P为流体承受的压力；Fx、Fy分别为流体所受体积力的x、y向分量.

2 参数定义

Re、Cd、St是描述绕流问题的几个常用的参数，它们的定义如下：

雷诺数：表征惯性力与粘性力的一个无量纲参数：

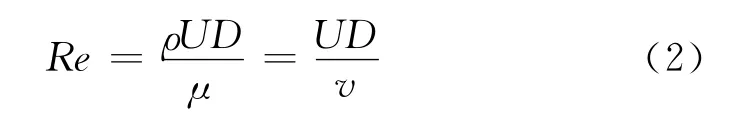
式中，ρ为流体密度；U为来流风速；D为柱体特征长度；μ、v分别为流体的动力、运动粘性系数.

阻力系数：阻力是流体对柱体的顺流方向的作用力，将阻力无量纲化得到阻力系数Cd

式中，Fd为流体作用于单位长度柱体上沿顺流方向的分力.

斯托罗哈数：描述旋涡脱落的一个重要的无量纲参数

式中，f为涡脱频率.

3 数值模型

当流体流过钝体的时候，由于流体本身粘性的作用，使得物体表面上的流体速度为零，而离开物体表面一定距离的流体速度则不受粘性影响，此处的流动可以按照无粘来处理.在物面和可以按无粘处理的流体之间的这一部分流体就是边界层.边界层通常是很薄的一层，但在这一薄层中各项流体参数却发生着剧烈的变化，存在着较大的速度梯度.因此，在绕流问题中精确地模拟边界层对于结果的重要性至关重要，这就要求边界层网格要足够密，如图1所示.本文流体计算域大小取为42D×24D，方柱与圆柱的特征长度D相等，沿展向的厚度取D／200.

图1 方柱、圆柱计算域及网格示意图

在通常的两方程涡粘性湍流模型中，k－ε模型能够较好地模拟远离壁面处已充分发展的湍流流动，kω模型则更广泛地运用于各种压力梯度下的边界层问题.而综合了两种模型各自优势的SST湍流模型，在近壁面处保留了原始的k－ω模型，而在远离壁面处应用了k－ε模型，这一特点使得采用SST湍流模型来模拟绕流问题结果会更为精确.CFX数值模拟计算时沿柱体厚度方向（展向）取为很薄的D／200，即用很薄的三维模型来模拟二维问题.Re≤500时采用层流模型，Re＞500时采用SST湍流模型（中等湍流强度5%；壁面取光滑壁面，无粗糙度）.计算域边界条件设置如下：

1）左侧：速度入口，U＝U0，V＝0；

2）右侧：出口边界条件，平均静压P为零；

3）沿展向两边界采用对称边界条件：各变量沿法向的分量为零；

4）其余边界采用无滑移固壁边界条件：U＝0，V＝0.

4 模型验证及参数分析

4.1 方柱绕流模型验证及参数分析

表1为方柱绕流模拟计算的各参数及相应的文献结果，其中Cd为瞬态计算时对应的阻力系数的平均值.

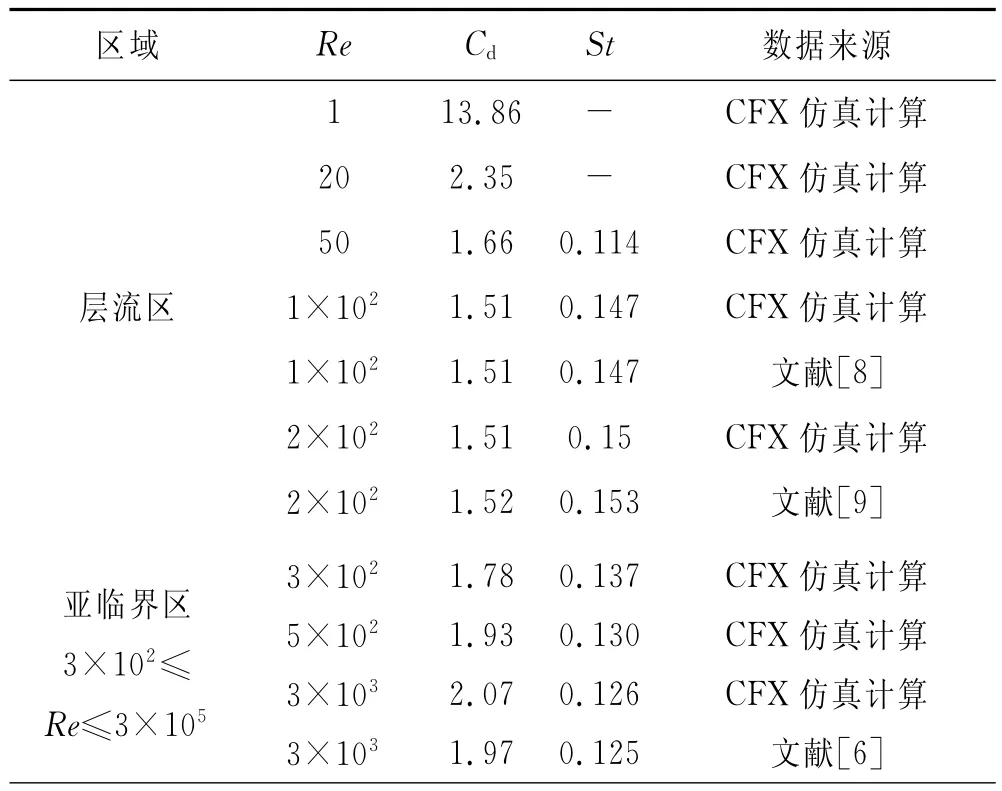
表1 方柱绕流数值计算各雷诺数下对应的参数结果及相关文献结果

续表1 方柱绕流数值计算各雷诺数下对应的参数结果及相关文献结果

由表1可知方柱仿真计算结果与现有文献结果吻合较好，最大误差为8%.从图2、3中也可以形象地看出本次计算结果与文献结果的拟合程度，这验证了本文方柱绕流模拟计算方法的正确性.方柱的St、Cd随Re的变化规律如图2、3所示，其中曲线为数值结果的拟合曲线，数据点为已有的文献数据.

由图2可知，方柱的St在Re＜50时为零，这是由于绕流还未产生旋涡的脱落；在50＜Re＜100时，St由零急剧增大，在Re＝200附近时达到最大；在200＜Re＜1 000时，St随着Re的增大又迅速减小，而在Re＞1 000后波动较小，稳定在0.126附近.由图3可知，对于方柱绕流，在Re＜100时Cd随着Re数的增大急剧减小.Re＞1 000以后，方柱的平均阻力系数值变得比较平稳，波动较小，稳定在2.1附近.

4.2 圆柱绕流模型验证及参数分析

由表2可知圆柱仿真计算结果与现有文献结果吻合得也比较好，从图4、5中也可以形象地看出本次计算结果与文献结果的拟合程度，这验证了本文圆柱绕流模拟计算方法的正确性.

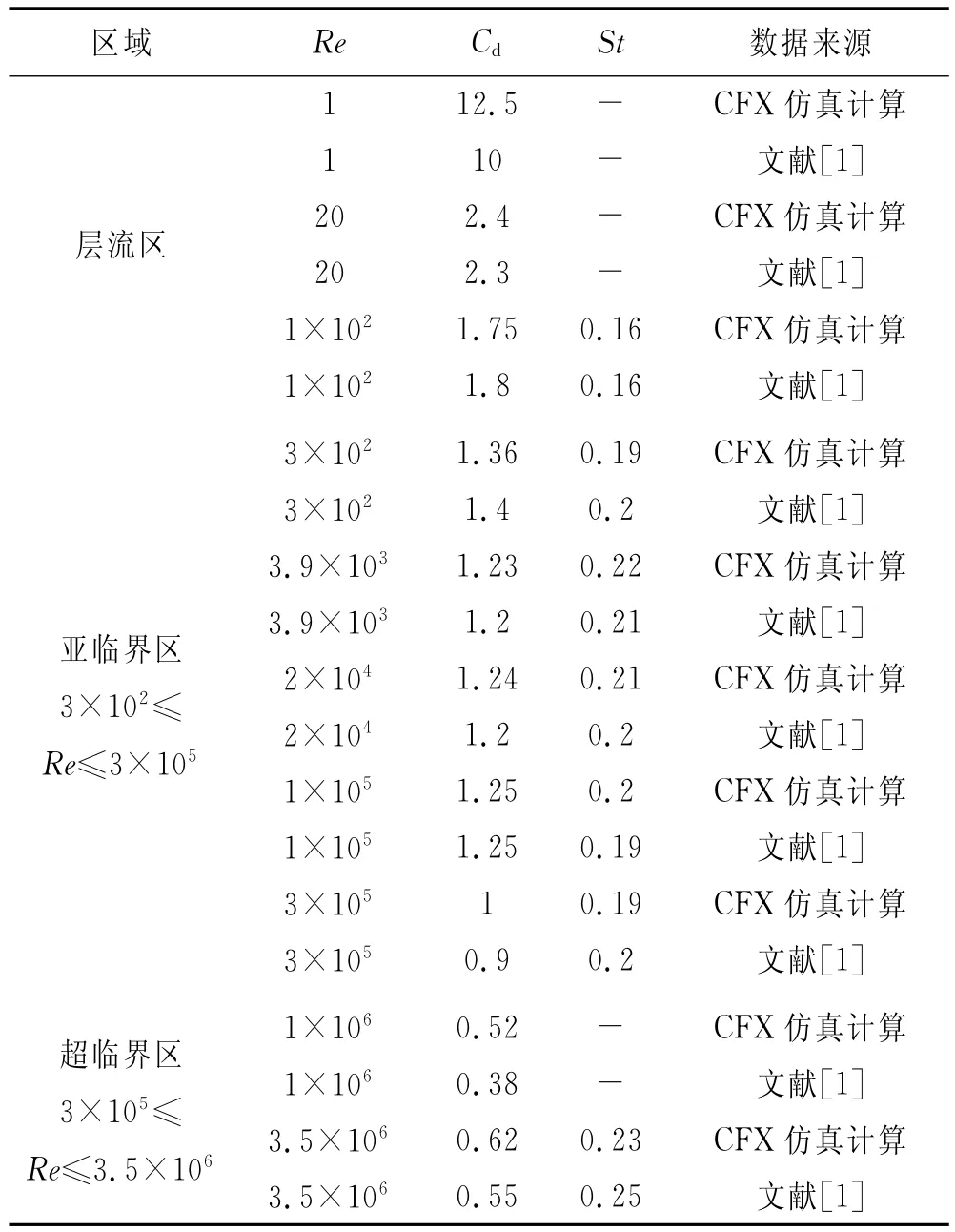
表2 圆柱绕流数值计算各雷诺数下对应的参数结果及相关文献结果

圆柱的St、Cd随Re的变化规律如图4、5所示，其中曲线为数值结果的拟合曲线，数据点为已有的文献［1]的数据.

图4 圆柱的St－Re曲线

由图4可知，圆柱的St在Re＜20时为零，因为此时绕流还未产生脱落的旋涡；在20＜Re＜300时，St由零急剧增大到0.2；在300＜Re＜3×105时，St在0.2附近轻微波动；而后，在Re＝1×106附近涡脱频率很混乱，没有稳定的St值，可推知此时已经不存在规则的涡街了；当Re＞3.5×106后St值又出现并呈现逐渐增大的趋势，可知此时规则的涡街又重新建立起来了.

图5 圆柱的Cd－Re曲线

由图5可知，对于圆柱绕流，在Re＜1 000时Cd随着Re数的增大由12.5急剧减小到1.2左右；Re＞1 000以后，圆柱的平均阻力系数值变得比较平稳，波动较小，稳定在1.2附近；在Re＝1×106附近，可以看到Cd值突然减小.此时边界层正经历着从层流分离向湍流分离的过渡阶段，旋涡脱落趋于不规则化，圆柱前方的正压值不变，后方旋涡脱落区的负压绝对值减小，导致流体对柱体的总压减小，阻力系数也随之减小.当边界层分离完全转化为湍流分离后，阻力值又会增大并趋于稳定.

4.3 方柱与圆柱绕流数值结果对比

为了分析方柱和圆柱绕流的不同，本文比较了方柱和圆柱数值模拟结果中的St、Cd随Re的变化规律，如图6～7所示.

图6 方柱、圆柱的St－Re曲线

图6为方柱和圆柱绕流St随雷诺数Re变化的比较，可以分为3阶段：第1阶段，旋涡开始脱落后，St随雷诺数Re的增大而迅速增加，方柱在Re＝200时达到极大值点，圆柱要在Re＝300左右才达到极大值点；第2阶段方柱在200＜Re＜1 000范围内的St开始缓慢减小，而圆柱的St在300＜Re＜3×105范围内基本上稳定在0.2；第3阶段方柱的St随雷诺数Re的变化趋于稳定的值，而圆柱的St却又开始增大.此外，第2、3阶段方柱的St一直小于圆柱的St.

图7为方柱和圆柱绕流阻力系数Cd随雷诺数Re变化曲线的比较，可见其整体趋势大体一致，但计算发现方柱不存在明显的阻力危机现象，这与两者的分离点位置的不同有很大的关系.圆柱绕流中流体边界层分离点会随着雷诺数的增大而逐渐后移，而方柱的分离点则固定位于其两个前角点处.在Re＜100时两者的Cd均随着Re数的增大急剧减小.Re＞1 000以后，方柱与圆柱的阻力值基本上变化幅度不大，但方柱的阻力值总是大于相应的圆柱的阻力值.

图7 方柱、圆柱的Cd－Re曲线

5 结 论

运用CFX可以较为精确地模拟方柱和圆柱的绕流问题，通过以上分析，可以得出以下结论：

1）方柱绕流中St值在较高雷诺数Re时是趋于稳定的，而圆柱绕流却不同，在稳定变化阶段过后，随着Re的增大St值又开始增大了.并且，在Re＞200后方柱的St值比圆柱的St值小37%以上.

2）对于方柱和圆柱绕流，在Re＜100时Cd随Re变化得很剧烈，而在Re＞1 000后，Cd随Re的变化基本上趋于稳定.在Re＞1 000后方柱的Cd值一直比圆柱的Cd值高60%以上，这是由方柱表面存在着4个尖锐的角点而圆柱表面比较光滑所致.

3）由于方柱的分离点始终位于其两个前角点不变，使得在圆柱绕流中明显存在的阻力危机现象，在方柱绕流中并不明显，亦或要在更大的雷诺数下才会发生.

［1]史里希廷 H.边界层理论（上册）［M].7版.徐燕侯，译.北京：科学出版社，1988.

［2]曹丰产，项海帆.圆柱非定常绕流及涡激振动的数值计算［J].水动力学研究与进展（A 辑），2001，16（1）：111－118.

［3]詹 吴，李万平.不同雷诺数下圆柱绕流仿真计算［J].武汉理工大学学报，2008，12（30）：129－132.

［4]Davis R W，Moore E F.A Numerical Study of Vortex Shedding from Rectangles［J].Fluid Mechanics，1982，116：475－506.

［5]Okajima A.Strouhal Numbers of Rectangular Cylinders［J].Fluid Mechanics，1982，123：379－398.

［6]Kim D H，Yang K S，Senda M.Large－eddy Simulation of Turbulent Flow Past a Square Cylinder Confined in a Channel［J].Computers ＆Fluids，2004，33：81－96.

［7]陈政清，项海帆.桥梁风工程［M].北京：人民交通出版社，2005.

［8]Singh A P，De A K，Carpenter V K.Flow Past a Transversely Oscillating Square Cylinder in Free Stream at Low Reynolds Numbers［J].International Journal for Numerical Methods in Fluids，2009，61：658－682.

［9]Wan D C，Patnaik B S W，Wei G W.Discrete Singular Convolution－finite Subdomain Method for the Solution of Incompressible Viscous Flows［J].Computational Physics，2002，18：229－255.

［10]Norberg C.Flow Around Rectangular Cylinder：Pressure Forces and Wake Frequencies［J].Journal of Wind Engineering and Industrial Aerodynamics，1993，49：187－196.

［11]Lyn D A，Einav S，Rodi W.A Laser Doppler Velocimetry Study of Ensemble－averaged Characteristic of the Turbulent Flow Near Wake of a Square Cylinder［J].Fluid Mechanics，1995，304：285－319.

［12]Ansumali S，Chikatamarla S S，Frouzakis C M.Entropic Lattice Boltzmann Simulation of the Flow Past Square Cylinder［J].Modern Physics，2004，15（3）：435－445.