蒙特卡罗法在热磨机磨片优化设计中的应用
马洪斌,马 岩,杨春梅
(1.哈尔滨理工大学机械动力工程学院,哈尔滨150080;2.东北林业大学研究生院,哈尔滨150040;3.东北林业大学林业与木工机械工程技术中心,哈尔滨150040)
蒙特卡罗方法 (Monte Carlo Method)被广泛应用在数学、物理、工程技术以及管理等诸多方面[1]。这种方法的特点是如果模拟的次数越多,那么其计算出的结果可靠性就会越大。蒙特卡罗方法特别适用于在计算机上对某些大型项目和新产品进行开发。针对一些含有大量不确定因素的复杂决策系统进行风险模拟分析和问题优化蒙特卡罗方法也同样适用。采取这种方法还可用于机械优化设计中有关随机方向搜索问题的研究[2,3]。
关于随机方向搜索优化的方法在各种参考文献中已有详细的介绍[4]。蒙特卡罗方法用于随机方向搜索方面有以下的特点:可以作为无约束优化方法,也可作为约束优化方法,再者其程序短、效率高、概念清晰。文中研究了蒙特卡罗方法的原理和其算法框图,并用其对热磨机磨片齿形进行结构优化设计。
1 蒙特卡罗优化算法原理
若有一优化问题,其数学模型为[5-7]:

这是一个n维的不等式约束优化问题,设变量x= [x1,x2,……,xn]T上下界限为:

其取值的平均值为:

按以下步骤进行搜索[4]:
(1)在初值给定以后,我们依据设计变量所确定的上、下界限来缩小一个范围,开始进行第j=1的第一轮随机搜索,得到i个点Xij。第一个确定了的缩小后的区间下限为:

若lk〈bk,则取:

再确定缩小后区间上限与下限之差:

若lk+uk〉uk,则取:

缩小后的区间定后,就可求到一个点Xijk(i=1~500,j=1~8,k=1~n):

RND(x)为一随机数,并且0〈RND(x)〈1。
(2)当获得此点后,再用约束条件来检查其是否可行,若不可行则再产生一个新点;若可行就以此计算出其目标函数f(x),把这个目标函数与事先给定的一个足够大的数M相比较,此时,若f(x)〉M则不采用,若f(x)〈M则采用,并且令f(x)⇒M。
(3)查看是否满足迭代终止条件的要求,若满足就可以停止收缩,然后转到步骤⑦;若不满足则再一次进行新的一轮搜索。
(5)针对每次搜索的结果,要不就是新点不符合可行性或下降性的要求,再有就是会都得到比上一次更好的结果,在搜索i=imax次以后,我们可以进一步围绕此点来缩小区间开始新的搜索,令j+1⇒j。
(6)在当搜索区间被缩小jmax次之后,如果仍没达到要求,我们可以把imax或jmax增加,然后重新搜索。
(7)搜索停止,然后输出结果。
2 蒙特卡罗热磨机磨片优化数学模型
本文所要设计磨片所要处理的浆种是漂白硫酸盐针叶材,这种原料的纤维平均长度为2.3~3.8 mm,平均宽度为39.8~47μm。采用的打浆方式为中等纤维长度的半粘状、半游离状浆。所配用电机功率为1400 kW,其转速为1500 r/min。磨片的规格为:外径1 070 mm,内径400 mm。选用材料为00Cr27Mo,该种材料的各项性能参数为:屈服极限为645 MPa,强度极限为810 MPa,许用应力为712 MPa,杨氏模量为805 GPa,泊松比为0.32,密度为 8 315 kg/m3。
2.1 未优化磨片参数的选定
(1)Bs的确定。
处理的浆种为半粘状、半游离状漂白硫酸盐针叶木浆,齿刃比负荷 Bs取2.5~3.0 J/m之间的2.6 J/m。
(2)磨片每转切断长的确定。
齿刃比负荷 Bs已选定。配用电机功率为1 400 kW,转速为1 500 r/min。该机的空载功率一般为240 kW,考虑实际生产中用于纤维分离的总功率一般在70%额定功率和满载之间,因此取中间值为1190 kW,则用于分离纤维的有效功率为:
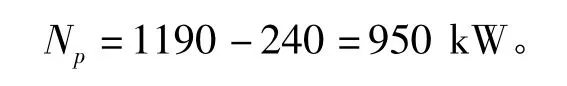
由下式可得磨片的每转切断长为:

(3)磨片齿纹类型的选择。
本文研究的磨片是圆环分区直长齿类型的磨片。该磨盘圆环被划分为破碎区、粗磨区和精磨区3个圆环区。各环的长度取值为:破碎区取90 mm,粗磨区取70 mm,精磨区取175 mm。粗磨区的刀齿由精磨区的刀齿相间延长,而破碎区的刀齿则由粗磨区的刀齿相间延长直至内圆边,即粗磨区的刀齿数为精磨区的刀齿数的一半,而破碎区的刀齿数为粗磨区的刀齿数的一半,这样取值便于设计和加工[8]。
(4)刀齿角度的选择。本文中刀齿角度取10°。
(5)刀齿齿长的计算。
首先计算精磨区齿长,磨片半径 (精磨区外径)为535 mm,粗磨区外径535-175=360 mm,刀齿角度10°。因此,由余弦定理可以算得:精磨区齿长为179.06 mm。以同样的方法可以算得粗磨区和破碎区的长度分别为71.53 mm和92.04 mm。
(6)齿宽、槽宽和齿数的确定。
精磨区的齿宽取4 mm,槽宽取8.5 mm,那么一个齿节长就是12.5 mm。由于磨片的齿数一般较多,所以齿节长与齿周节长可以被近似看作相等为12.5 mm。那么精磨区的齿数就为1 070×3.14/12.5=268.78,在这里为了便于等分,取齿数为268。
由于精磨区的齿数为268个,故对应的粗磨区的齿数为268/2=134个,破碎区的齿数为134/2=67个。那么,粗磨区外圆边一个齿节长约为(1 070-350) × 3.14/134=16.8 mm,若粗磨区的齿宽仍取4 mm,则粗磨区的槽宽就为12.8 mm。同理,破碎区上单个齿节长为 (1 070-490)×3.14/67=27.2 mm,如果破碎区的齿宽取8 mm,则槽宽为19.2 mm。
下面对切断长是否符合要求进行验证。
已知精磨区齿长为179.06 mm,齿数为268个,则精磨区的切断长为:
268 ×268 ×0.17 906=12 860.80 544 m/r。
粗磨区齿长为71.53 mm,齿数为134个,则粗磨区的切断长为:
134 × l34 ×0.07 153=1 284.3 927 m/r。
破碎区齿长为92.04 mm,齿数为67个,则破碎区的切断长为:
67 ×67 ×0.09 204=413.1 677 m/r。
所以,总的切断长为:14 558.36 568 m/r。该值与需要切断长的偏差为0.39%,基本上吻合要求。因此,各环的齿宽、槽宽、齿数确定依次为:精磨区的齿宽为4 mm,槽宽为8.5 mm,齿数为268个;粗磨区的齿宽为4 mm,槽宽为12.8 mm,齿数为134个;破碎区的齿宽为8 mm,槽宽为19.2 mm,齿数为67个。
(7)齿高的确定。本文中齿高取7 mm。
(8)数据汇总。齿纹类型及刀齿数据汇总见表1所示。

表1 齿纹类型及刀齿数据Tab.1 Types of tooth line and data of disc tooth
2.2 磨片参数优化模型
齿高δ影响浆料在磨区的通过量和磨片的使用寿命,磨片齿角度β和热磨机的泵送作用相关,磨片齿数Z和齿长L是磨片的重要评价指标,本研究主要选这四项参数进行优化。
(1)取设计变量为:

公式 (8)中表示磨盘内动盘和定盘刀齿的数目,其是参与热磨的最重要参数;L表示磨盘第i段内每秒切断长,它往往决定了纤维的长度;δ分别是动盘刀齿的高度或定盘刀齿的高度,具体数值由磨盘的强度来确定;β是动盘和定盘上刀齿和半径方向所成的夹角。整个数学模型的建立就是要对所设的参数和设计变量间的对应关系进行蒙特卡罗的优化,以便后续推理论证的实现。
(2)其目标函数为:

由公式 (10)、公式 (11)和公式 (12)以及破碎区的取值90 mm,粗磨区的取值70 mm,精磨区的取值175 mm,再者粗磨区的刀齿数为精磨区的刀齿数一半,破碎区的刀齿数为粗磨区的刀齿数一半,可以得到上述公式 (9)所列的目标函数。由于V=πDn及Np均已知,磨片动盘的破碎区、粗磨区、精磨区每个区内齿数Z、齿高L、齿长δ和定盘的相同,β大小相等方向相反,式中引入的这些设计变量做为优化的目标函数,这些设计变量与所需论证的目标函数的关系可以保证目标函数的齿刃比负荷为最小值。Z为磨盘动盘和定盘刀齿数目;L为刀齿长度,m;δ为分别为动盘刀齿的高度或定盘刀齿的高度,m;β为动盘和定盘上的刀齿和半径方向所成的夹角;具体的上下界限数值在约束方程中给出,经过蒙特卡罗的推理与本文的基本假设,作为蒙特卡罗数学模型推导出来的优化目标函数是实现最佳求解的前提。

式中:Fi为磨盘第i段内刀齿的接触面积,m2;Zpi,Zci为磨盘第i段内动盘刀齿数和定盘刀齿数;δpi,δci为磨盘第i段内动盘刀齿和定盘刀齿的厚度,m;Li为磨盘第i段刀齿的长度,m;βpi,βci为动盘和定盘上刀齿和圆盘直径方向所成角度。

式中:Np为纤维分离时的有用功率,W;μ为纤维分离系数;V为动盘圆周速度,m/s;F为动盘刀齿和定盘刀齿的接触面积,m2。
式中:Pa为a区内刀齿间的平均比压,Pa。
(3)确定设计变量的上下界限作为输入参数:


(4)确定约束条件。
动盘和定盘第i区约束条件为:

式中:Z为磨盘第i段内动盘和定盘刀齿数目;n为热磨机动盘转速,r/sec;L为第i段内动盘刀齿长度和定盘刀齿长度,m;δ为分别为第i段内动盘刀齿高度和定盘刀齿高度,m;β为动盘和定盘上的刀齿和半径方向所成的角度;
上述就是动盘、定盘的约束条件,公式 (13)和公式 (15)与已知纤维最小长度有关,公式(14)与磨片的接触面积有关 (取一般经验值),引入到公式中并加以详细的推导,在这里对动、定盘的约束条件是一样的,因为他们是反对称的。
3 蒙特卡罗随机数产生
在用蒙特卡罗方法进行优化的时候,要产生各种概率分布的随机变量。本研究取基本的 [0,1]上均匀分布的随机变量的抽样值作为随机数[9]。
为了产生随机数,本文在EXCEL中采用VB编程产生随机数,产生500个随机数的分布如图1所示,随机数均值为0.48803642037187、方差为0.29281305430389、最大值和最小值分别为0.99964045453800 和 0.00011744955560。此方法产生的随机数为伪随机数,在实际应用中这些伪随机数可以当作真正的随机数使用。如图1所示。

图1 500个随机数分布图Fig.1 Distribution of 500 random number
4 蒙特卡罗优化算法框图
根据上述的蒙特卡罗算法原理,可以总结画出蒙特卡罗优化算法的框图,如图2所示。

图2 蒙特卡罗优化算法框图Fig.2 Chart of optimization algorithm for Monte Carlo
用Visual Basic编制蒙特卡罗算法程序,可以得到经过优化后的精磨区齿角度、齿长、齿数、齿高的数据,通过进一步计算可以得到粗磨区和破碎区的相应数据,具体数据见表2,定盘的参数与动盘的参数值相同,齿角度取相反值。

表2 优化后的齿纹类型及刀齿数据Tab.2 Types of tooth line and data of disc tooth after optimization
通过表1和表2的数据可知,该设计外径42英寸的磨片在经过优化后的齿角度增加了3°,精磨区、粗磨区以及破碎区的齿长和齿高都有所增加,而齿数则有所减少,在此条件下对纤维的处理时间会比较理想,但如果再增加磨片尺寸,那么相应的每秒切断长和平均比压都会随之升高,热磨机对纤维的处理时间也就会随之增长。表2中提到的“优化后的齿纹类型及刀齿数据”在上述的论证中并没有被特定的指出,但在实际工程中,齿纹类型是圆环分区的形状,本文采用的是最简单的直长齿。刀齿数据包括表中的所列数据。鉴于对优化模型的精度要求,使得文中的理论数据在应用中要略有修改。
5 结束语
本文首先介绍了蒙特卡罗方法的算法和原理,并针对传统设计方法的局限性,采用蒙特卡罗方法来进行热磨机磨片磨齿部分的优化设计。建立了蒙特卡罗热磨机磨片优化设计数学模型,并基于此模型对热磨机磨片进行了优化设计。在热磨机磨片优化设计过程中引入了蒙特卡罗方法。依据确定出的热磨机磨片特征参数,通过产生随机数并建立蒙特卡罗数学模型求解,从而获得优化了的磨片参数值。
[1]黄宏新,曹泽星.优化量子Monte Carlo计算中的波函数[J].湖南大学师范大学自然科学学报,1996(4):62-65.
[2]李国云,王 忠.蒙特卡罗法在机械优化设计中的应用[J].攀枝花学院学报,2009(6):63-66.
[3]丁柏群,张 鹏.蒙特卡罗模拟信号交叉口的服务水平[J].森林工程,2006(3):35-37.
[4]刘星荣,方 珉.蒙特卡罗法在汽车变速器可靠性优化设计中的应用[J].轻型汽车技术,1998(5):4-8.
[5]覃 岭,周 华,谢君生,等.汽车自动变速器检测设备传动系统的优化设计[J].现代机械,2008(3):9-12.
[6]张利伟,王 伟.基于参数化建模有限元优化技术[J].水科学与工程技术,2008(2):18-20.
[7]李宜海.机械优化设计的数学建模及求解中的几个问题[J].煤矿现代化,2008(3):80-81.
[8]史玉梅.圆环直齿热磨机磨片的设计分析和结构优化[D].长春:吉林大学,2007.
[9]姜 慧,崔国民,倪 锦.能量系统广义换热网络优化的蒙特卡罗SCDD法[J].华北电力大学学报:自然科学版,2010(1):92-95.

