基于辅助图最短路算法的程序设计及应用
高 燕
(河北省高速公路青银管理处)
自1962年提出求解网络最大流的第一算法—标号法以来,不少学者开始应用数学网络理论对路网系统进行研究并提出计算路网容量的模拟方法和数学模型,近几年,对于路网容量的研究得到很大进展,最大流理论也有所应用。但是以往应用最大流理论对路网容量的计算方法在对路网简化和计算量上各有缺陷,不方便应用到计算机程序设计中。因此从另一个角度入手,寻找一种更适合于编程计算的最大流最小割算法。利用基于辅助图的最短路算法来代替最大流最小割算法就是一个很好的途径,辅助图最短路算法适应于单起终点的无向网络,可以应用到可平面化的道路网络中,不仅可以简单处理路网,而且该算法能够输出确定的网络中任意两个节点之间的流量值。
1 对路网的抽象简化
第一,路网应该简化为无向网络更为合理,因为在道路网络中,每个路段一般都是双向的,即使有单向街道也往往在很接近的地方有对向的平行街道与之相匹配。以往的辅助图最短路算法从理论上提出了路网应该简化为无向网络,但是在实例处理时体现不够,即一般来讲基于此,提出对无向网络进行测算的方法。
第二,无向图的可行流,大多表现在多收发点的多种物流上。以往算法大都将其简化到确定的几个网络节点上,即车站、码头和机场等重要的交通集散点。虽然这种简化有一定的合理性,但是这样找到的最短路可能不是整个网络中的最短路,即可能存在非收发点之间的最短路,其值小于收发点之间的最短路的值。通过对算法输出进行改进,将辅助路网内部任意两个节点之间的最短路径,即原路网任意两个节点之间的最大流输出并进行分析。
2 对最短路算法的改进
利用以上算法,首先将现状路网转化成可以利用最短路算法求解最小割的路网模式,包含收发点选取、边权赋值、构造辅助路网等,应用Matlab 软件,选取Dijkstra 算法对最短路径部分进行计算机编程。本算法不但应用先进的软件工具进行编程,而且对程序输出显示进行改进,可以输出辅助路网中任意两点的最短路径和最大流量,程序的算法流程图见图1。
3 算法实例
如图2 所示,该通道网络的起点为v1,终点为v6,通道的通行能力用标注在路线旁边的数字表示。下面以图2 为例,给出本算法的应用过程。

图1 算法流程图

图2 通道网络简化图
下面开始构造该网络的辅助图,如图3 所示,G 中存在多少个内面,G*就可以产生多少个中间点与之对应;另外,G*的起点和终点位于G 的上面和下面。辅助图中各边的权值与原路网中与之相交的G 中的边权一一对应。

图3 辅助路网图
根据以上两图写出辅助图路网的路线权值矩阵,这个矩阵不但可以表示辅助图当中各个节点的连通状况,而且能表示各条路线的通行能力。两点之间没有直接通路的路线权值应该无限大,即无路可走,这里根据实际情况用一个较大的数表示,该路网选取100(远远大于有连接通路的其它节点之间的权值即可)。矩阵如下

将初始矩阵读入计算机程序当中,利用Matlab 软件程序可以计算出路网最大流量矩阵和路网中任意两点之间的最短路径。
最大流量矩阵如下

从路网容量矩阵可以看出,原路网的最大流量为M16=9,即原通道网络图中从v1到v6的最大流量为9。另外该矩阵还输出任意两点之间的最大流Mij,除了始、终结点之间的容量外,其它内部结点之间的路网容量虽然不符合路网容量的定义,但是能够反映路网中内部流量情况。
最短路矩阵Rij记录从点到点的最短路径的中间结点,该路网最短路矩阵具体如下

最短路径确定方法为
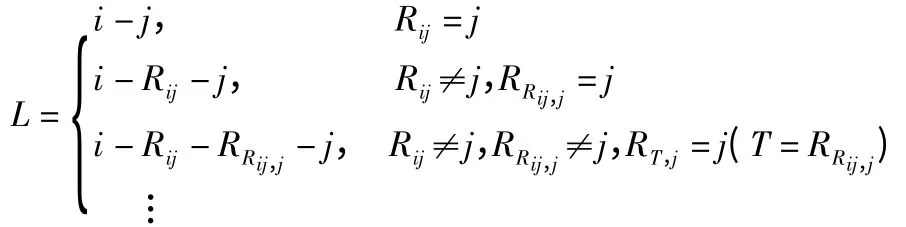
由此可以看出,辅助图G*的最短路是1.5.6,最短路的值为9。与之相对应的原路网的最小割集是(v3v6、v5v6),最小割集容量是9。
4 小 结
在已有算法的基础上,通过改进得到了求无向路网中所有最小割集的较为简便的算法,通过构造辅助路网并求其最短路,利用Matlab 计算机语言程序实现该算法,并且可以根据需求输出辅助网络中任意两点间的最短路和原路网任意两点的最大流,不但减少了计算量,而且提高了该算法应用于计算机上的可靠性。将该算法应用于可平面化的实际路网中,可以快速找到路网的关键断面,即运输通道的瓶颈,为路网规划和改建扩建提供理论依据。
[1]杨涛,徐吉谦. 运输网络极大流的一种新算法[J]. 土木工程学报,1991,24(2).
[2]陈春妹.路网容量研究[D].北京工业大学,2002.
[3]杨晓萍.基于网络最大流理论的城市道路网容量研究[D]. 哈尔滨工业大学,2004.

