在线报价系统中销售商的风险定价策略

周振红

(湖北经济学院工商管理学院，湖北 武汉 430205)

随着Internet在电子商务中的广泛应用，一些企业开始尝试一些创新性的定价模式。1998年Priceline.com公司提出了一种独创的商业经营模式，即 NYOP(name your own price)模式，也称作消费者定价模式，自该模式出现以来就受到广大顾客和航空公司的喜爱。

Priceline.com公司的NYOP定价模式[1]在竞争异常激烈的美国市场脱颖而出，引起了学术界的关注，许多学者开始对这种交易模式进行研究。HANN和TERWIESH研究了在NYOP中的消费者行为，该模式允许消费者重复报价，但会产生大量的摩擦成本[2]。其研究表明消费者可以通过学习以前报价的经验来降低摩擦成本。TERWIESH等用动态规划模型求解消费者在可以多次报价情况下的最优报价策略，但是当消费者第一次报价被拒绝后，如果他们继续报价，则会产生更大的摩擦成本[3]。TERWIESH等得出了消费者报价的最优次数及最优报价值，并且提出了最优的限制价格。还有学者如SCOTT、MARTIN和GERARD等从其他角度研究了在线报价系统中销售商限制价格的制定策略问题[4－10]。但在研究销售商的限制价格的制定时，这些研究基本都以直接求取销售商的最大期望收益的方式来确定销售商的限制价格。

在现实生活中，销售商的目标往往是多重的，在保证获得一定利润的条件下，谋求销售收入最大化，是企业行为的多目标模式中最常见的。它最早是由美国经济学家鲍莫尔提出来的。该模式假设:一旦企业的利润达到可以接受的水平，企业的利润目标与增加销售收入的目标相比，就会处于次要地位。这时，企业经理宁可放弃较高的利润，也要追求更大的销售收入。鲍莫尔认为，企业之所以要追求最大的销售收入，是因为销售收入是衡量企业绩效的重要尺度。其大小反映消费者对产品的认可程度、在市场上的竞争地位和企业的经营规模，所有这些对于提高企业的活力都是十分重要的。此时，原有通过求取销售商的最大期望收益来确定价格的方法就不适用了。针对这类问题，考虑到在线报价机制下的销售量具有不确定性，即任意一个价格都可能使销售量达到理想值，只是达到理想销售量的概率不同而已，此时需要制定一个价格使其达不到理想的销售量的概率是最小的，即在定价中除了考虑销售商期望收益外，还要考虑使销售量达不到目标值的风险最小，也即销售商的风险定价。

1 问题描述

在NYOP模式中，需要购买商品的顾客登录网站提供身份证明(或注册一个新用户)后就可以对需要的商品进行报价，报价系统获得顾客的报价信息后将其与销售商制定的内部限制价格作比较，如果顾客的报价高于限制价格，那么交易成功，顾客以自己的报价获得商品;若低于限制价格，那么交易不成功，并且系统不允许顾客对同一种商品重复报价。这种销售模式可用图1表示。

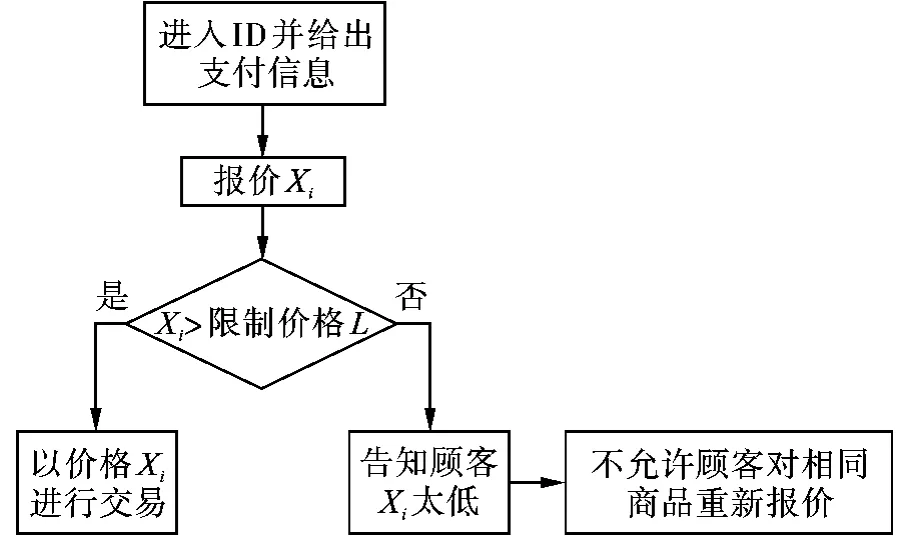
图1 顾客交易过程描述

笔者以图1为基本销售模式，研究在产品的库存和销售期有限并考虑到顾客保留价格分布的情况下，保证销售商的销售量大于目标量的概率不低于理想值条件下销售商的限制价格制定策略。

2 模型建立

2.1 顾客的最优出价模型

对于通过NYOP购买商品的顾客来说，他面临如下的决策问题:顾客不知道销售商制定的内部限制价格，如果他的报价高于限制价格，他将获得收益(顾客对商品的估价与他报价之间的差异)，当然也要付出相应的成本，并且顾客也会认识到他的出价可能较高从而让销售商获得更多的额外利润。如果顾客的报价低于限制价格，他将得不到任何收益，还招致因等待等原因造成成本损失，这与文献[2，3，8]中所列的前提条件和符号相一致。在这里，同样假定顾客是风险中性的，用c表示顾客报价的成本，用L表示由销售商决定而顾客未知的限制价格。还假定顾客最初认为L是一个在区间[Rmin，Rmax]上服从均匀分布的自由变量。并且Rmax－Rmin＞c。

保留价格为r的顾客报一个价格x∈[Rmin，R*]，这里 R*=min(r，Rmax)，如果 x ＞ L，交易成功，顾客以自己的报价获得产品，实现r－x－c的消费者剩余;然而若x＜L，报价被拒绝，交易不成功，顾客招致损失c。

命题1若销售商的限制价格L是在区间上[Rmin，Rmax]的均匀分布。那么，当顾客的保留价格为r时，其最优的报价为:

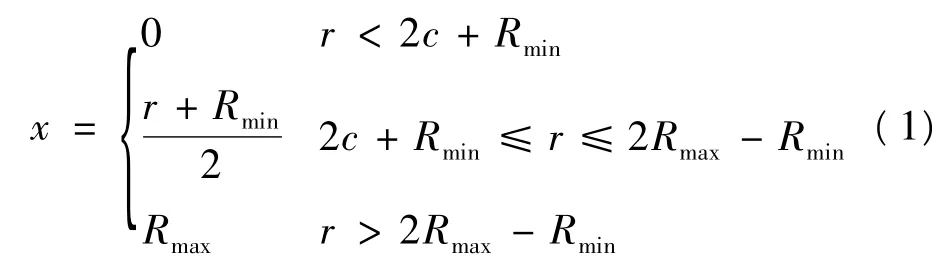
其中，x=0意味着顾客不报价。

证明由于顾客只有一次报价的机会，顾客的保留价格为r，顾客在NYOP系统中所报的价格为 x∈[Rmin，R*]，那么，当 x＞L时，交易成功，顾客以自己的报价获得产品，实现r－x－c的消费者剩余;然而若x＜L，交易不成功，顾客招致损失c。若销售商的限制价格L服从密度函数为f(L)(L∈[Rmin，Rmax])的分布，那么，该顾客获得的期望消费者剩余便为:

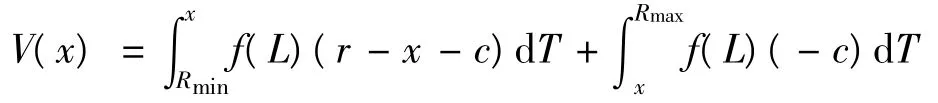
若L在区间[Rmin，Rmax]上服从均匀分布，则:

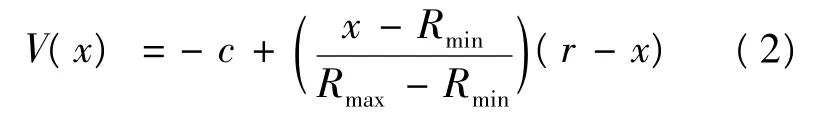
这里(x－Rmin)/(Rmax－Rmin)即为顾客的报价x超过L的概率。

顾客进行报价，其目的是想获得最大的期望消费者剩余，于是，顾客的最优报价为:

2.2 销售商的最优限制价格规划模型

为了便于分析，引入以下的符号和约定:

(1)假定每个顾客至多购买一件商品。

(2)假定销售商要求实际销售量大于销售目标量d的概率不得低于α。

(3)假定顾客的保留价格是私有信息，也就是每位顾客知道自己的保留价格，但不知道其他顾客的保留价格，只了解其分布函数。参照BRITRAN等[11]对顾客需求模式的设定，假设市场中潜在顾客实际在网上报价率服从泊松分布。虽然不同顾客的保留价格不同，但是能通过设定不同的参数来充分表现顾客的异质性，从而反映出顾客报价的变化。假定顾客的保留价格的分布函数采用参数为m尺度、参数为v的威布尔分布，其密度函数为 f(r)=mv(vr)m－1e－(vp)m，累积的概率分布函数为 F(r)=1－e－(vr)m，其中，r为顾客的保留价格。

(4)设潜在顾客的到达率为λ(t)，一般情况下，对于时间的推移引起顾客到达率变化可以有两种形式:一是线性趋势，即λ(t)=λ0+βt;二是指数趋势，即 λ(t)= λ0e－ρt，考虑计算的便利性，选用线性趋势。

那么，当 L∈[Rmin+c，Rmax]时，由命题 1 可知:保留价格为r的顾客能成为销售商的实际需求者的条件是:即 r≥2L－Rmin。于是，在销售期间销售商的实际需求率为:

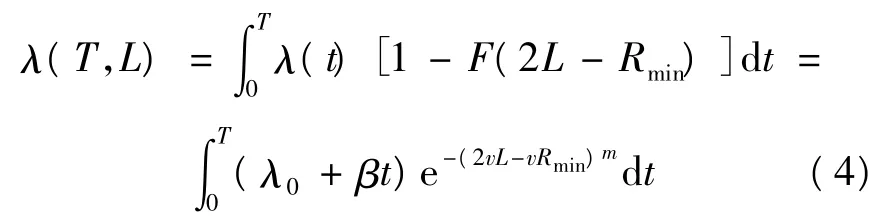
易知，在其他条件不变的情况下，λ(T，L)是随L从+∞趋于0的连续减函数，其最大值在L=Rmin+c时取得。

由于假设市场中潜在顾客实际在网上报价率服从泊松分布，因此，限制价格若为L，有j位顾客购买商品(或是销售j件产品)的概率为:

于是，理性的销售商在设定的目标销售量d和实际的销售量大于销售目标量d的最低概率α就应满足:

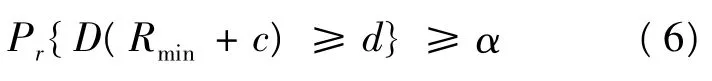
又因为假定到达的顾客数量与顾客的报价无关，那么，根据贝叶斯公式，顾客的最优报价超过销售商限定价格L的条件概率密度函数为:

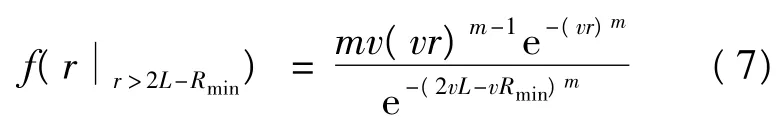
由于假定到达的顾客数量与顾客的报价无关，且只有在顾客的报价高于限制价格时商品才以顾客的报价成交，那么，在销售商要求实际的销售量大于销售目标量d的概率不得低于α条件下，销售商的最大期望收益数学规划模型为:

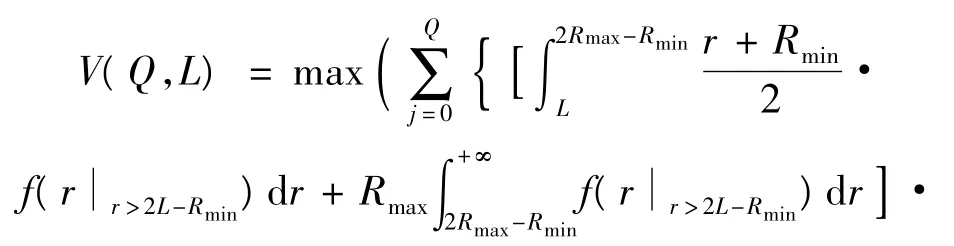
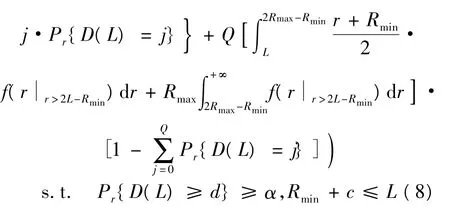
将式(5)、式(7)代入式(8)，求出L的解为L*，当 L*∈(Rmin+c，Rmax]时，销售商的最优限定价格为 L*;当 L*=Rmin+c时，区间[Rmin，Rmin+c]上的任何一个值均为销售商的最优限定价格。

命题2对于威布尔分布中的任意参数，由式(8)决定的数学规划模型具有如下性质:①②式(8)有解。

3 数值分析

在该算例中，取 λ0=2，v=0.045，m=4，Rmin=50，Rmax=200，c=2，T=10，Q=20。考虑到式(8)计算的复杂性，借用Mathematic 5.0为数值分析工具。

(1)在其他条件不变的情况下，考虑销售商不同最低概率阈值与最优的限制价格问题。取β = －0.02，d=10，α 分别为0.800、0.820、0.840、0.860、0.880、0.900、0.920、0.940、0.960、0.980时最优限制价格和对应的最大期望收益如表1所示。从表1可以看出在其他条件不变的情况下，销售商要求实际的销售量大于销售目标量的概率不得低于α，若α从一个较低的水平不断增大，那么，起初它的增加对销售商的最优限制价格和对应的最大期望收益没有什么影响，但随着α的不断增大，销售商的最优限制价格和对应的最大期望收益就下降，但销售商的最大期望收益的下降率并不大，如α从0.860增加到0.880时，销售商的最大期望收益却从2 300.970下降到2 300.010，下降了0.042%。也就是说，有时销售商适当增加实际销售量超过目标销售量的概率阈值，相应降低限制价格，可确保一定的产品市场占有率，它对销售商的收益影响并不大，这对销售商也许是个不错的选择。

(2)在其他条件不变的情况下，考虑销售商目标销售量的不同最低概率与最优的限制价格问题。取 β= －0.02，α =0.700，d 分别为 7、8、9、10、11、12、13、14、15、16 时最优限制价格和对应的最大期望收益如表2所示。从表2可以看出在其他条件不变的情况下，若销售商的销售目标量d从一个较低的水平不断增大，那么，起初它的增加对销售商与最优限制价格和对应的最大期望收益没有什么影响，但随着d的不断增大，销售商的最优限制价格和对应的最大期望收益就下降，但销售商的最大期望收益的下降率并不大，例如，d从12增加到13时，销售商的最大期望收益却从2 300.92下降到2 295.31，下降了0.24%。也就是说，有时在同等的最低概率要求下，销售商适当增加目标销售量，相应降低限制价格，可确保一定的产品市场占有率，它对销售商的收益的影响并不大，这对销售商也许是个不错的选择。

表1 销售商不同最低概率限制与最优的限制价格和对应的最大期望收益

表2 销售商不同目标销售量与最优的限制价格和对应的最大期望收益

4 结论

笔者假定顾客到达服从泊松分布，顾客的到达率随时间变化，假定顾客对购物品进行报价，顾客的报价是私有信息，其他人不知道其具体值，只了解其分布函数，销售商销售库存有限、商品具有时效性，同时要求实际的销售量大于目标销售量的概率不低于某个阈值时，讨论销售商的最优限制价格的制定策略问题。笔者建立了在线销售商的随机收益模型，并采用Mathematic 5.0对模型进行了数值分析，得到如下结论:

(1)销售商要求实际的销售量大于销售目标量的概率不得低于α时，若α从一个较低的水平不断增大，那么，起初它的增加对销售商的最优限制价格和对应的最大期望收益没有什么影响，但随着α的不断增大，销售商的最优限制价格和对应的最大期望收益就开始下降，但销售商的最大期望收益的下降率并不大。

(2)在其他条件不变的情况下，若销售商的销售目标量d从一个较低的水平不断增大，那么，起初它的增加对销售商的最优限制价格和对应的最大期望收益没有什么影响，但随着d的不断增大，销售商的最优限制价格和对应的最大期望收益就开始下降，但销售商的最大期望收益的下降率并不大。

因此，有时在销售商适当地增加实际销售量超过目标销售量的概率阈值或在同等的最低概率要求下销售商适当地增加目标销售量，相应地降低限制价格，可确保一定的产品市场占有率，对销售商的收益的影响并不大，这对销售商也许是个不错的选择。

[1] 徐雅卿，魏轶华，胡奇英.基于Priceline的买方/卖方定价收益管理问题[J].管理科学学报，2008，11(3):63－69.

[2] HANN I H，TERWIESH C.Measuring frictional cost of online transaction:the case of a NYOP － retailer[J].Management Sci，2003，49(11):1563 －1579.

[3] TERWIESH C，HANN I H，SAVIN S.Online haggling at a name－your－ own－price retailer:theory and application[J].Management Sci，2005，51(3):339 －351.

[4] SCOTT F.Partial－repeat－bidding in the name－your－ own － price channel[J].Marketing Science，2004，23(3):407－418.

[5] MARTIN S，BERND S，BJORN S.Measuring individual frictional costs and willingness－to－pay via nameyour－ own － price mechanisms[J].Journal of Interactive Marketing，2004，18(4):22 －36.

[6] DING M，ELIASHBERG J，HUBER J，et al.Emotional bidders an analytical and experimental examination of consumers'behavior in a priceline－like reverse auction[J].Management Sci，2005，51(3):352 － 364.

[7] MARTIN S，GERARD J T.Does the internet promote better consumer decisions?the case of name－yourown － price auctions[J].Journal of Marketing，2006，70(1):65－78.

[8] 周振红，黄深泽.顾客网上讨价还价最优出价问题[J].系统管理学报，2008，17(6):660－664.

[9] 周振红，黄深泽.在线报价系统中销售商最优限制价的制定[J].统计与决策，2008，27(22):59－61.

[10] JOHN G W，ZHANG G R.Optimal design of a name－ your － own － price channel[J].Journal of Revenue and Pricing Management，2008，7(3):281 －290.

[11] BRITRAN G R，MONDSCHEIN S V.Periodic pricing of seasonal products in retailing[J].Management Sci，1997，43(1):64 －79.