集群式供应链供应商间的库存互补优化
黄纯辉,张庆年,周兴建,刘春玲
(1.武汉理工大学交通学院,湖北 武汉 430063;2.武汉纺织大学供应链系统研究中心,湖北 武汉 430073)
库存互补是供应链管理研究的重点之一,它是指供应链位于同一链节的企业间,由于物料的相似性和可替代性,在紧急缺货的条件下,互通有无的库存协作方式。在有关供应链库存互补问题的文献中,研究主要集中在两个方面:一是针对同一单链式供应链某链节中,多个(两个以上)同质企业间库存互补;二是针对不同单链式供应链,位于相同某链节的两个企业间库存互补。其中,有的针对供应链下游存在着多个零售商的客观现实,考察了同一单链式供应链下两个零售商之间的库存互补[1-2];有的则将互补的零售商由两个扩展到N个,并将这种位于零售链节的零售商库存互补分析,由原来建立在链内企业间的合作,拓展到链与链合作的背景下[3-4];有的考虑了供应链零售商的紧急库存互补渠道来自于另外一个供应链的零售商,分析了其行为结果对整个供应链系统的库存总体水平的影响[5-6]。
但上述文献都是考察零售商环节的库存互补,没有考察供应链零售商以外的链节企业之间的库存互补问题,特别是基于不同两单链,上游供应商之间的库存互补,即紧急情况下,除了同一供应链通过正常订货渠道外,还存在着来自另外一邻近供应链供应商的紧急库存互补,即基于两单链的集群式供应链供应商间的库存互补,这种跨链间的库存互补不仅影响被补充单链下游企业的库存协作水平,而且也影响提供补充单链各链节企业的决策行为。
1 基本模型
笔者考察的集群式供应链系统由两个单链式供应链组成,每个单链式供应链包括一个分销商、一个生产商和N个供应商,即生产商生产一个产品,需N个供应商为其提供配件或原料,如图1所示。
当然,这种互补存在是基于BOM中一对也可能是多对供应商之间的耦合互补。总之,长期的竞合博弈使供应商认识到,不仅各供应链节点企业内部之间需相互协作,而且不同单链的企业也需跨链间的协调,才能有效放大整个集群地的市场份额,从而得到整体利润的提高。

图1 基于BOM耦合的集群式供应链供应商跨链间库存互补系统结构图
2 系统仿真模型建立
2.1 单链系统模型
在单链式供应链系统中,假设包含了N个供应商、一个生产商和一个分销商,各节点企业均采用定期订货方式(fixed - interval system,FIS)[7],即一种按预先确定的订货间隔期进行订货的库存管理方式。假设供应商、生产商和分销商在每个周期期初检查库存,而供应商的生产量与生产商、分销商订货量的大小需要从两方面考虑,即一是订货以下游企业的订货量为依据,二是希望通过订货来校正库存,使之达到期望库存。其中,供应商A生产量是其库存调节率与生产商的平均订货率之和,当 AVORDERF.K+AINVRS.K≤0时,生产量为0;当 AVORDERF.K+AINVRS.K >0时,生产量的DYNAMO方程式表示为:

其中,生产商的平均订货率(AVORDERF)是一个延迟函数。

库存调节率是期望库存与当期的实际库存之差与调节时间之商,通过这个调节率,可以调整供应商的生产率,避免生产过多造成库存积压,从而减少库存费。

供应商A库存量(AINVS)的DYNAMO方程可表示为:

生产商实际使用配件量(ZPABC)的DYNAMO方程可表示为:

顾客服务水平是库存量与顾客需求量之商,即:

供应链SC库存总量为供应商、生产商和分销商库存量的总和,具体方程为:INVZ.K=AINVS.K+BINVS.K+CINVS.K+INVF.K+INVD.K。
牛鞭效应的量化采用上游企业订单量的标准差与下游客户需求的标准差的比值来表示:

供应链总物流成本包括运输成本、库存持有成本和缺货成本,具体的计算公式如下:

在系统动力学模拟软件Vensim上,描绘出各变量的相互关系,可得单链式供应链系统动力学仿真模型,如图2所示。
2.2 跨链间库存互补系统仿真模型

图2 单链式供应链系统动力学仿真模型(基于3个供应商)
集群式供应链跨链间库存补充是一种紧急库存互补,在正常情况下,两单链各供应商分别为各自的下级生产企业提供配件,只是在面临需求变化而某单链的供应商不能及时满足下游生产商需求的情况下,同一环节的供应商之间才相互紧急补货。例如,SC1的供应商1A只有在其服务水平少于目标值(假设为0.95),不能及时组织生产满足生产商订货需求时,才会向另一供应链的供应商紧急订货,而当SC2的供应商2A有多余的库存商品时,才会为SC1的供应商1A提供紧急库存补充。因此,当供应商 1A的服务水平ASCRS1≥0.95时,SC1的供应商1A的紧急补货为0;当 ASCRS1<0.95时,SC1的供应商1A向SC2的供应商2A提出紧急订货要求,SC2的供应商2A则根据自己的库存量来决定是否为SC1的供应商1A提供补货,当SC2的供应商2A的库存量AINVS2大于SC1的供应商的缺货量(SAQ1)时,紧急补货(ASENDS21)等于SAQ1;当AINVS2.K<SAQ1.K时,紧急补货量等于AINVS2。
其中,SC1的供应商1A的缺货量(SAQ1)是由某一周期的生产商订货量(ORDERF1)和供应商1A的期初库存量(AINVSX1)来决定的,当AINVSX1.K≥ORDERF1.K 时,供应商1A 的缺货量为0;当 AINVSX1.K<ORDERF1.K 时,缺货量的DYNAMO方程式为:
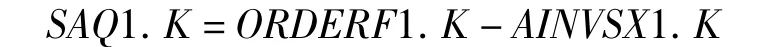
而SC1的供应商1A的生产量是其库存调节率、生产商平均订货率,以及SC2的供应商2A平均缺货率之和,当AINVARS1.K+AVORDERF.K+SAQ2.K≤0 时,生产量为 0;当 AINVARS1.K+AVORDERF.K+SAQ2.K >0时,生产量的DYNAMO方程式为:

其他供应商(B,C,…,N)相关变量的DYNAMO方程与供应商A相类似。
3 仿真结果分析
3.1 牛鞭效应分析
笔者采用Vensim进行模拟仿真。以牛鞭效应、供应链库存总量、顾客服务水平和供应链总物流成本作为系统的评价指标,模拟时间为200周,步长为1周;两单链式供应链各自的顾客需求均服从[200,250]的均匀分布;两供应链各级成员库存量的初始值均为相应的期望库存值,而期望库存等于平均发货率(或销售率)乘以期望库存能够满足平均销售率的周数(假定为1周)。
在基于BOM耦合的供应商跨链互补下,考察集群式供应链两单链的分销商、生产商和供应商订单量相对于最终顾客需求的放大,以分析所产生的“牛鞭效应”,即当市场上一种商品的消费需求发生细微变动时,这种波动会沿着分销商、生产商和供应商逆流而上,并逐级扩大,导致在达到最终源头供应商时,其获得的需求信息和实际消费市场中的顾客需求信息存在较大的偏差[8-10]。
牛鞭效应比较分析如表1所示。由表1可知,基于BOM耦合的不同供应商跨链间紧急库存互补,均能使供应链系统的牛鞭效应明显减弱。优劣次序是:三对供应商库存互补>两对供应商库存互补>单对供应商库存互补,其中以三对供应商库存互补系统的牛鞭效应减弱最多,供应链SC1的分销商、生产商和供应商相对于顾客需求的牛鞭效应分别为 1.57、2.00 和 2.59;供应链SC2的分销商、生产商和供应商相对于最终顾客需求的牛鞭效应分别为 1.09、1.28 和 1.68。无论是SC1还是SC2,牛鞭效应不仅优于原单链式供应链,而且胜过单对供应商库存互补和两对供应商库存互补系统。

表1 牛鞭效应比较分析
3.2 供应链库存总量和物流成本分析
供应链库存总量和物流成本分析仿真结果如表2所示。供应商跨链间库存互补,也能改善供应链系统的性能,其中以三对供应商库存互补系统效果最好,该系统下,SC1和SC2的库存总量和物流成本平均值比单链式供应链系统分别减少了28.98%和6.56%、59.88%和23.53%,随着互补对数的增加,两条供应链的库存总量和物流成本均呈现不断下降的趋势。因此,通过对SC1和SC2库存总量和物流成本的分析,也从侧面进一步证明了基于BOM耦合的供应商库存互补程度较高时,不仅能较好地提高各单链运作效率,而且为整个集群式供应链协调提供了一种较好的范式。

表2 供应链库存总量和物流成本比较分析
3.3 顾客服务水平分析
顾客服务水平分析仿真结果如表3所示。结果表明通过供应商跨链间库存互补,能使供应链的顾客服务水平在一定程度上得到提高。在4种模式中,以三对供应商库存互补系统效果最好,该系统下,SC1和SC2的顾客服务水平平均值比单链式供应链系统分别提高了10.11%和28.73%,随着供应商互补级数的增加,供应链的顾客服务水平呈现曲线上升的态势。
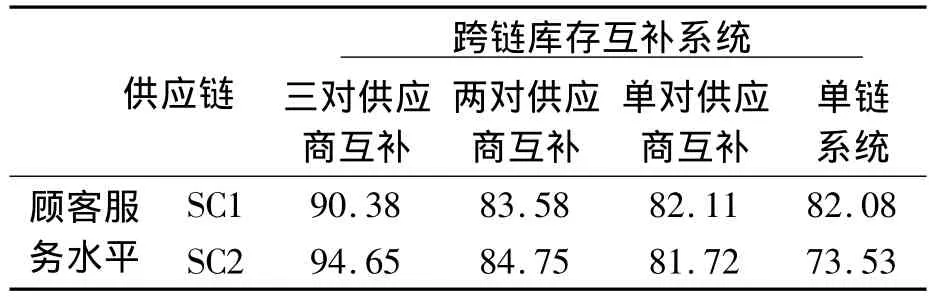
表3 顾客服务水平比较分析 %
4 结论
笔者研究了基于BOM耦合的供应商跨链间库存互补情况,分别讨论了单对、两对和三对供应商库存互补对集群式供应链系统的牛鞭效应、库存和顾客服务水平的影响。结果表明,不同程度的供应商紧急库存互补,都能有效地从供应源头抑制顾客需求波动、减少供应链系统的库存总量和总物流成本、减弱牛鞭效应、提高顾客服务水平,其中以三对供应商库存互补模式最优。但是笔者只研究了供应商库存互补问题,当生产商、分销商均进行库存互补时,能否进一步优化集群式供应链系统性能,将是今后的研究方向。
[1]XU K,EVERS P T,FU M C.Estimating customer service in a two-location continuous review inventory model with emergency transshipment[J].European Journal of Operational Research,2003(3):569 -584.
[2]BURTON J,BANERJEE A.Cost- parametric analysis of lateral transshipment policies in two-echelon supply chains[J].International Journal of Production Economics,2005,83(2):169 -178.
[3]BANERJEE A,BURTON J,BANERJEE S.A simulation study of lateral shipments in single supplier,multiple buyers supply chain networks[J].International Journal of Production Economics,2003,81(1):103 -114.
[4]KUKREJA A,SCHMIDT C P.A model for lumpy demand parts in a multi-location inventory system with transshipments[J].Computers and Operations Research,2005,32(8):2059 -2075.
[5]黎继子,刘春玲.集群式供应链跨链间的库存协调模型研究[J].系统工程与电子技术,2007(9):1479-1483.
[6]黎继子.集群式供应链管理[M].北京:中国经济出版社,2007:25-61.
[7]梁志杰,杜文,文军.确定性联合补充库存问题的模拟退火算法[J].系统工程理论方法应用,2005(1):201-209.
[8]达庆利,张钦,沈厚才.供应链中牛鞭效应问题研究[J].管理科学学报,2003(3):124 -129.
[9]刘春玲,孟波,黎继子.基于两单链合作下的集群式供应链牛鞭效应分析及仿真研究[J].中国管理科学,2007(1):63-67.
[10]李柏勋,黎继子.集群式供应链多周期随机库存系统模型与仿真[J].统计与决策,2007(4):134 -136.

