基于SVM的我国商业银行风险预警研究

陈朝晖，胡玉芳

(福州大学管理学院，福建 福州 350002)

随着我国金融领域开放程度的加深，银行业所面临的经营环境更加不确定。设计适合我国实际情况的银行风险预警模型，避免危机的爆发或降低危机的破坏性，具有重要的理论与现实意义。

1 文献回顾

自20世纪80年代开始，以统计学习理论为基础的小样本、非线性机器学习方法，即支持向量机(SVM)越来越受到研究者的青睐。

国外对SVM的预测效果进行了大量的研究。SHIN等[1]采用SVM方法对公司破产风险进行预测，并将其与BP神经网络方法进行比较，结果显示:当训练样本比较小时，SVM的预测精度和总体效率都比 BP神经网络高。CHEN等[2]采用SVMs、BP神经网络及Logit回归方法构建了银行风险预警模型，结果显示SVMs模型的预测效果和准确率远远高于其他两个模型。BOYACIOGLU等[3]以土耳其被储蓄存款保险基金接管的银行为样本，对神经网络、支持向量机和多元统计预警模型进行了比较分析，结果显示，SVMs具有较好的预警效果，预测准确率达到90.9%。

国内对SVM的应用主要体现在对银行信贷风险的识别与分类上。余晨曦等[4]将支持向量机的非线性分类器应用到贷款违约的判别中，构建了基于支持向量机的我国商业银行信用风险度量模型，并将结果与多元线性判别分析的结果进行了对比。结果显示，支持向量机在对贷款违约的判别中有很好的判别效果。吴冲等[5]建立基于模糊积分的支持向量机集成方法对商业银行信用风险进行了五级分类，评估结果表明，该评价方法具有科学、简洁、预测精度高等特点，且模型的结构与方法应用前景广阔。类似的研究还有汪晓玲[6]、成洪静[7]等。以上SVM 方法下的风险识别大多只针对银行的单项风险，而在银行综合风险研究中的应用较少，笔者将采用SVM方法来构建我国商业银行综合风险预警模型。

2 SVM模式识别原理

2.1 线性SVM模式识别

对于两类模型识别问题，学习的目的是构造一个决策函数(分类线或分类面)，使训练样本中的正、负两类样本分别位于该线或平面的两侧。然而，满足条件的线性决策函数存在无数条划分直线，如图1所示。

基于此，VAPNIK提出了间隔最大化原则。如图2所示，H为最优分类线，H1、H2分别是由样本中离最优分类线最近的样本(支持向量)所决定且平行于最优分类线的直线，二者之间的距离即为分类间隔，H与H1、H2的距离等于1/2分类间隔。间隔最大化原则是指寻求使分类间隔达到最大的最优分类线(面)。

SVM是从线性可分情况下的最优分类面发展而来的。设二类线性可分样本集(Xi，yi)，X∈Rd，i=1，2，…，n，yi∈{1，－1}的决策函数为:

图1 决策函数存在无数条划分直线

图2 间隔最大化原则图

对判别函数f(X)=(WXi)+b进行归一化，使所有样本都满足即离最优分类面最近的样本其中，H1:WXi+b=1，H2:WXi+b=－1，(WXi)+b=0为最优划分超平面的方程。由此，两类样本的分类间隔为2/‖W‖。依据VAPNIK的间隔最大化原则，可以把问题归结为求解如下二次凸规划问题:

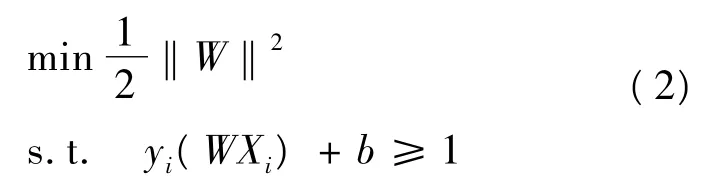
根据KKT约束条件αiyi(WXi)+b－1=0，将上述问题转化为对偶规划问题，可以解出最优解α*及对应的w*和b*，进而求得最优超平面决策函数:

对于线性不可分的函数集，可以通过引入松弛变量ξi(≥0)加以修正。ξi为样本Xi偏离所属类别边界的距离，该值越大偏差也就越大;C为惩罚系数，表示对错分的惩罚力度。类似地，可求如下凸规划问题及相应的决策函数:

2.2 非线性SVM模式识别

对于非线性模式识别问题，SVM通过非线性映射把样本空间映射到一个高维特征空间，使原来的非线性问题在特征空间中变为线性问题，从而在高维特征空间中用线性支持向量机解决样本空间中的非线性分类问题。被积函数乘上一个二元函数再做积分，其结果为一个新的函数:

其中，λi、ψi(x)分别为核 K(x，y)的特征值和特征向量。作原样本空间X到特征空间F(由Mercer核的特征函数构成的函数集)的非线性映射φ为:

原线性可分函数中的 x和 xi用 φ(x)和φ(xi)替换，可在特征空间F中应用线性支持向量机求其最优超平面决策函数:

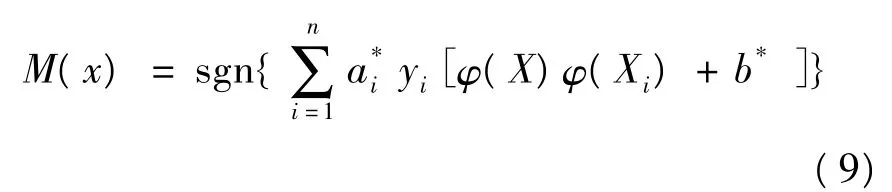
根据Mercer定理，可化简为:

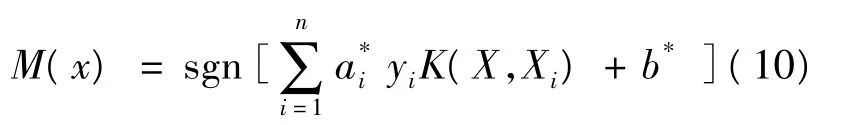
比较常见的Mercer核有多项式核函数K(x，xi)= [(xxi)+1]q、径向基核函数及 Sigmoid核函数，K(x，xi)=tan h[v(xTxi)+c]等。

2.3 “一对一”多类SVM模式识别

SVM是一种性能优良的二元分类器，但在实际问题中，多数待识别的模式是多类别的。对于多类划分问题，可通过构建多个SVM分类器的方法将其转化为多个二分类问题加以识别。主要的SVM多类划分方法有一对多、一对一及有向无环图，其中，一对一方法应用最为广泛，且稳定性和准确率较高，因此选用该方法来识别银行风险类别。基本思路是:选取K类中的任意两类样本来训练SVM子分类器，训练产生K(K－1)/2个SVM子分类器;将所要分类的数据分别输入这K(K－1)/2个子分类器中测试，并记录其在各个分类器中被分入的类别;最后累积计算其被分入各类的次数，累积次数最多的类别即为该数据所属的类别。

3 商业银行风险预警SVM模型的实证分析

3.1 银行风险预警指标体系的建立

从宏、微观的角度选取指标构建商业银行风险预警体系，各指标预警区间的划分主要参照国际标准、我国监管部门的相关规定，以及对已有专家、学者研究成果的整理。具体指标及相应阈值的确定如表1所示。

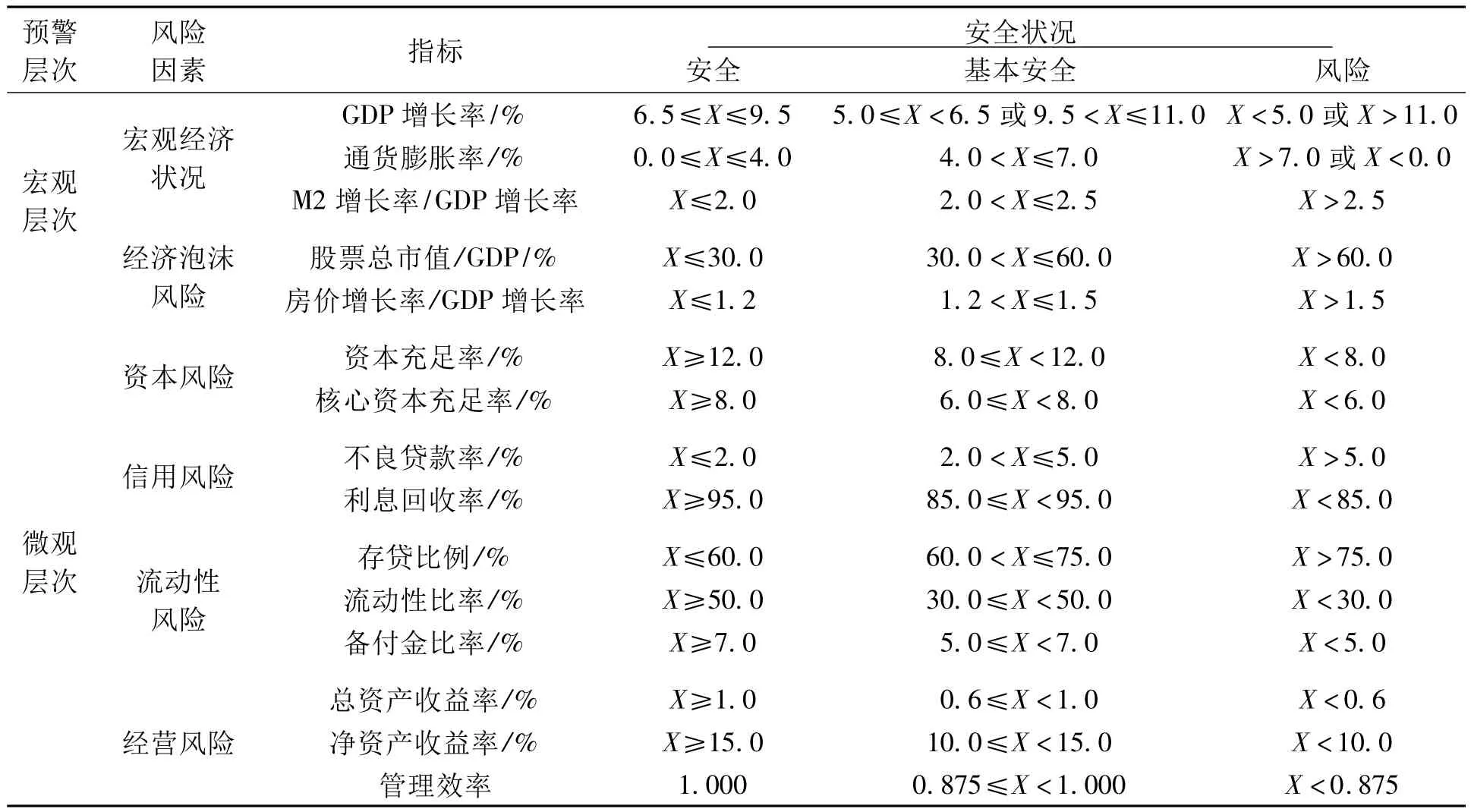
表1 我国商业银行风险预警指标体系[8－9]

其中，管理效率指标采用数据包络分析(data envelopment analysis，DEA)方法进行计算[10]。以固定资产、员工人数和存款总额作为投入变量，以利润总额和贷款总额作为产出变量，将来自2001至2009年末上市银行年度数据，剔除缺失值后的样本总量为81。其中，各样本的宏观指标数据主要摘自中国统计年鉴和中国金融统计年鉴，微观数据来自上市银行年度报表。这81个样本的投入、产出指标用DEAP软件计算出来的效率值分布情况如表2所示。

表2 我国商业银行管理效率指标值分布情况

在样本银行效率值中，最大值为1.000，最小值为0.656，平均值为0.877。笔者以平均值作为区分银行是否处于风险区间的阈值，效率值小于平均值的为风险银行，效率值大于平均值、小于1.000的为基本安全银行，而效率值等于1.000的为安全银行。最后，所有样本当中，12个样本的管理效率指标值处于安全区间，31个处于基本安全区间，38个处于风险区间。

3.2 数据的选取与处理

实际所选各指标与风险大小之间可能存在3种关系:指标值越大，风险越大;指标值越小，风险越大;指标值在某一区间内银行处于安全状态，而指标值越偏离这一区间，对应的风险越大。为了根据各银行风险综合得分的大小对银行进行风险归类，需要统一各指标与风险的变动方向，即指标值越大，风险越大。对各类指标的同趋化处理结果及处理后指标的预警阈值如表3所示。

此外，为了消除不同指标变量的量纲差异对实证结果可靠性的影响，先对数据进行归一化处理，将各指标的取值范围限定在[0，1]之间。归一化处理采用的是最大最小值法。

3.3 商业银行风险预警度评估

将原样本划分为两大类:以2009年前的样本数据(67个)来构建SVM模型，同时，用所构建的SVM模型对2009年的银行(14个)风险类别进行预测。首先需要运用主成分分析法计算2009年前样本数据的风险综合得分，据此划分各年度各银行所处的风险级别。Bartlett's检验的Sig.值显著为0，拒绝了相关矩阵是单位阵的假设，即变量间具有较强的相关性;KMO统计量为0.523，表明这些变量间存在着一定程度的信息重叠，适合采用主成分分析法。

表3 商业银行风险预警指标的同趋化处理结果

样本的前7个主成分基本保持了原来15个变量的信息，累积方差贡献率达到86.02%(大于85%)，故提取这7个主成分为计算银行风险综合得分的基础。求出7个主成分的因子得分F1、F2、F3、F4、F5、F6和 F7，并以旋转后各因子的方差贡献率占这7个因子方差贡献率之和的比例为权重进行加权汇总计算银行的综合风险得分F。其中，由基本安全阈值与风险阈值构成的虚拟基本安全银行与风险警戒银行的风险综合得分如表4所示。

当某综合风险得分F≤基本安全值时，该银行处于安全区间;当基本安全值＜F≤警戒值时，处于基本安全区间;而当F＞警戒值时，处于风险区间，依次将各银行归入安全、基本安全及风险3个区间。最终获得5个安全样本，42个基本安全样本和20个风险样本。

3.4 商业银行风险预警SVM模型的建立与检验

3.4.1 预降维处理

由于样本容量仅为67，而每一个样本为15维指标，这种小样本、高维度数据会影响到学习机的识别准确率和运行效率。因此，在模型构建之前，应先对样本数据进行降维预处理。在保证降维后的指标对原始指标具有至少90%解释力的前提下实施降维，降维后的指标维度与其解释力之间的关系如图3所示。

表4 虚拟安全银行与风险银行综合得分

图3 降维后的指标维度与其解释力的关系

由图3可看出，仅需保留前7个维度指标就可达到对原15维指标90%以上的解释力，SVM模型的输入变量是各样本的这7维指标值。

3.4.2 核函数的选择及参数的优化

核函数是实现SVM算法中将问题由输入空间映射到高维空间的关键因素，不同核函数采用不同的支持向量机算法，其形式与参数决定了分类器的类型和复杂程度。由于RBF核函数中只有一个参数g是可调节的，模型的运算难度大为降低;同时，已有研究表明，RBF核函数在大多情况都优于其他函数，具有较强的通用性。因此，选用RBF作为SVM分类核函数。

在确定了核函数之后，需要确定SVM模型中的两个重要参数:惩罚因子C和RBF核函数参数g。所采用的参数优化方法为K次交叉验证法，其基本思路是:把训练样本集分成K份大小一样的子集，取其中的一个子集为测试集，而将其余的K－1个子集合并作为训练集，用该测试子集去检验训练集上训练分类器的精度;如此依次循环，直至每一个子集都被测试一次，训练和测试分别进行K次;同时，设定参数C与g的变化范围和每次变化的步径大小，对每组变化的(C，g)分别完成如上的K次循环;最后，选取交叉验证准确率最高的分类器所对应的(C，g)作为最优的参数值。

寻优的结果显示:交叉验证准确率最高为84.905 7%，所对应的最小 C值为138，g值为0.088 4，它们即为所构建SVM模型的参数值。

3.4.3 模型检验及预测结果分析

选定了核函数和模型参数后，根据相应的具体参数采用“一对一”方法来构建SVM银行风险预警模型，并对其准确率进行验证。模型训练结果显示:在14个预测样本中，有13个都得到了正确的归类，预测精确率达到92.86%。以上是对2009年前的样本进行一次随机抽样得到的训练样本和测试样本的实证结果，为了克服随机性对SVM模型的影响，对原样本进行了多次随机抽样，构建多个基于不同随机训练样本与测试样本的SVM模型，观察其测试准确率是否有较大差异。基于10次随机抽样的SVM预测准确度分别为:92.86%、78.57%、92.86%、84.62%、92.86%、92.86%、84.62%、84.62%、84.62%、83.33%。基于10次随机抽样所构建的SVM模型对测试样本的分类预测准确度的均值为87.18%。由此可见，采用SVM构建的模型对于非线性关系和小样本模型具有较高的预测准确度，在银行风险预警中具有较好的预警效果。因此，接下来以2009年前的所有样本来训练、构建银行风险预警模型，并用该模型对2009年综合风险状况未知的14家上市银行的风险状况作出预测，预测结果如表5所示。

表5 采用SVM构建的模型对2009年14家上市银行风险预测表

4 结论

笔者采用SVM方法构建了我国商业银行综合风险预警模型，预警结果显示，2009年我国银行业总体风险状况并不乐观，在14家上市银行中有8家处于风险区域，6家基本安全，而没有一家是完全安全的。除宏观因素外，银行的盈利能力、风险管理水平等也是评判其综合风险大小的基础，各风险指标与综合风险间的关系是非线性的，并不能直接看出它们贡献的大小，但对照各预测样本的指标值与风险分类结果可以大致看出，模型的预测结果对识别银行风险状况具有一定的参考价值。

[1] SHIN K S，LEE T S，KIM H.An application of support vectormachines in bankruptcy prediction model[J].Expert Systems with Applications，2005(28):127 －135.

[2] CHEN W H，SHIH J Y.Astudy of Taiwan's issuer credit rationg systems using support vector machines[J].Expert Systems with Applications，2006(30):427 －435.

[3] BOYACIOGLU M A，KARA Y.Predicting bank financial failures using neural networks，support vector machines and multivariate statistical methods:a comparative analysis in the sample of savings deposit insurance fund transferred banks in Turkey[J].Expert Systems with Applications，2009(36):3355 －3366.

[4] 余晨曦，梁潇.基于支持向量机的商业银行信用风险度量模型[J].计算机与数字工程，2008，36(11):10 －14.

[5] 吴冲，夏晗.基于五级分类支持向量机集成的商业银行信用风险评估模型研究[J].预测，2009，28(4):57－61.

[6] 汪晓玲.基于SVM的银行客户个人信用评估研究[D].西安:西北工业大学图书馆，2007.

[7] 成洪静.基于SVM的银行信贷风险评估模型研究[D].太原:太原科技大学图书馆，2008.

[8] 王岚.开放条件下商业银行风险预警指标体系[D].郑州:河南大学图书馆，2009.

[9] 孙小琰，沈悦，亓莉.开放条件下我国银行安全预警指标体系研究[J].管理世界，2007(9):150－151.

[10] 包艳霞.我国上市商业银行X效率的实证分析[D].重庆:西南大学图书馆，2009.