天津市能源消耗与产业结构的相关性分析

李春发，谭洪玲，王澜颖，李 勇

(天津理工大学管理学院，天津 300384)

近年来，随着天津市经济高速发展，产业规模不断扩大和能源消耗持续增长，经济发展和约束能源消耗增长的矛盾日益突出。2009年天津市能源消耗总量达5 847万吨标准煤，是2000年能源消耗总量的2.2倍，年均增长率达13.5%。2009年天津市的能源生产总量为3 471.63万吨标准煤，其中原油生产量约占94.52%，天然气生产量约占5.48%。发电、供热和燃烧用煤完全依靠从外省调入，能源对外依存度较高。伴随能源消耗量的大幅增长，天津市经济也迅猛发展。2009年天津市全市生产总值达7 521.85亿元，是2000年国民生产总值的4.4倍，年均增长率达37%。图1为天津1978—2009年能源消耗量和相应的三次产业产值。从天津市三次产业结构看，2009年第一产业完成增加值128.85亿元;第二产业完成增加值3 987.84亿元;第三产业完成增加值3 405.16亿元，三次产业比例为2∶53∶45。

2011年是天津市“十二五”规划的开局之年，按照“十二五”期间单位GDP能耗降低20%的节能目标，天津市节能降耗的形势严峻。如何优化产业结构，解决社会发展和约束能源消耗增长的矛盾是天津市面临的紧迫问题。笔者从历年天津市能源消耗、国民经济发展水平和产业结构发展状况入手，研究能源消耗总量与经济整体发展水平及三次产业发展水平之间的长期和短期均衡关系，力图从降低能源消耗的角度，为天津市产业结构优化调整提供参考。

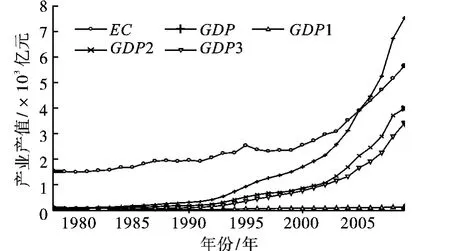
图1 天津1978—2009年万吨标准煤能源消耗量与产业产值

1 能源消耗与产业发展的相关研究

1978年，KRAFT等[1]在研究中首次发现美国GDP与能源消耗之间具有因果关系。此后，协整理论逐渐被应用到能源消耗与经济增长关系的研究中。YU和CHOI[2]运用因果关系研究发现，韩国存在从GDP到能源消耗的单向Granger因果关系，菲律宾存在从能源消耗到 GDP的单向Granger因果关系，而英国、美国和波兰，其GDP与能源消耗间却不存在显著的因果关系。NACHANE运用协整分析和向量误差修正模型对11个发展中国家和5个发达国家的数据进行因果关系检验，研究得出这16个国家的能源消耗与经济产出之间存在着长期的均衡关系。MASIH等[3]利用多变量的协整分析方法和向量误差修正模型，发现我国台湾地区1955—1990年的能源消耗、价格水平与真实收入之间存在协整关系，并且能源消耗与真实收入之间还存在双向的Granger因果关系。

自格兰杰因首创协整理论而获得2003年诺贝尔经济学奖之后，国内大量介绍或应用协整理论的文献涌现出来。林伯强[4]基于协整理论和误差修正模型研究发现GDP、资本和人力资本与电力消耗之间存在协整关系。韩智勇[5]等对1978—2000年中国能源消耗与经济增长的相关数据进行研究后得出:中国能源消耗与经济增长之间存在双向的Granger因果关系，但不具有长期的协整性。马宏伟[6]等检验了1978—2006年我国能源消耗总量与国民生产总值及三次产业产值之间的协整性和Granger因果关系，并建立向量误差修正模型。于全辉[7]等运用面板数据构建能源消耗与经济增长的协整分析模型，其研究认为:中国东西部地区能源消耗与经济增长之间的长期关系表现出显著的地区差异，东部地区能源消耗与经济增长之间的关系比西部地区更为密切。闫笑非和杜秀芳[8]认为:从短期来看，能源消耗量变化对我国第一、第二产业产值增长的影响各不相同。从长期来看，能源消耗对我国第一、第二产业产值增长具有同向拉动作用。吴巧生和成金华[9]对比分析了美国与中国能源的消耗与经济增长的协整关系，认为中国、美国的GDP增长均是能源消耗增长的原因，但美国比中国的因果关系更为显著。

综上所述，国内外学者对产业结构与能源消耗之间的关系进行了大量理论和实证研究。已有研究主要是基于对国家层面数据进行分析，对具体地区进行深入研究较少。由于不同省份和地区在发展水平、产业结构和能源消耗上存在较大差异[10]，因此，深入到省份和地区对能源消耗与产业结构之间关系进行研究很有必要。笔者基于历年天津市能源消耗与产业发展的相关数据，构建相关计量经济模型，对能源消耗与产业结构之间的变动关系进行深入分析。

2 能源消耗与产业发展的相关性检验模型

2.1 变量的选取和数据的来源

根据数据的可得性及科学性原则，笔者选取1978—2009年天津市国内生产总值、三次产业相应的生产总值(单位:亿元人民币)和能源消耗总量(单位:万吨标准煤)作为样本数据。其中历年国内生产总值及三次产业的产值以1978年的不变价格计算实际国内生产总值。所有数据均来自于相关年份的《天津统计年鉴》。同时，为了减少时间序列的异方差性，将原始数据中的总量指标全部进行了对数处理，并用LECt表示t年的能源消耗总量，用LGDPit表示t年第i产业国内生产总值，用DLECt和DLGDPit分别表示t年能源消耗总量和第i产业产值的一阶差分。

2.2 变量的单位根检验

当时间序列为非平稳时，一般会导致“伪回归”现象，因此在建立模型之前必须对变量进行平稳性检验，以确定各序列的平稳性和单整阶数。单位根检验是判断变量是否平稳的常用方法。笔者选用ADF法对变量进行单位根检验，得到各变量序列的平稳性分析结果，如表1所示。

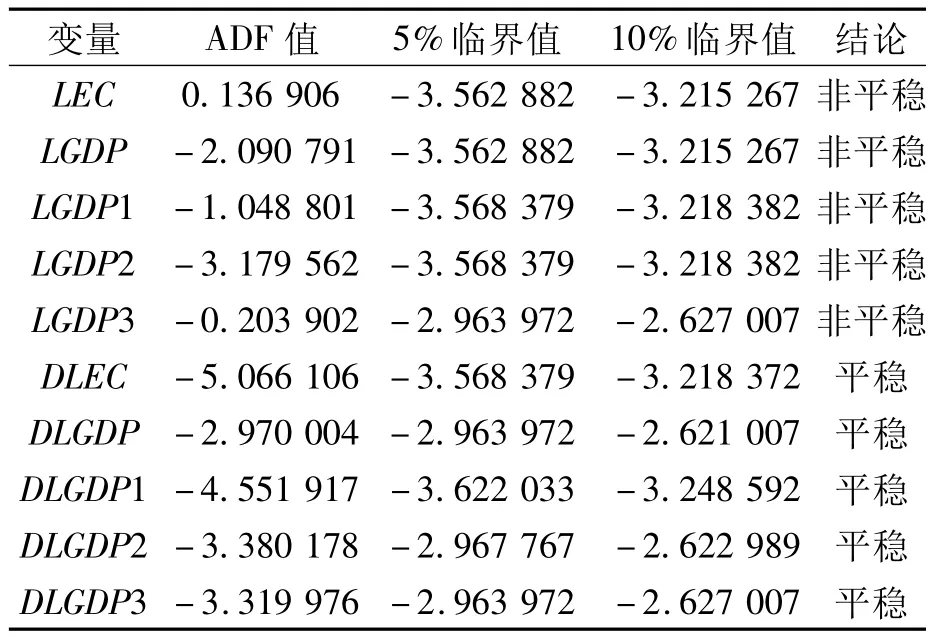
表1 各变量序列的单位根检验结果(ADF检验)

通过ADF检验结果可知，经过一阶差分后序列 DLEC、DLGDP、DLGDP1、DLGDP2、DLGDP3 均拒绝存在单位根的假设，即为平稳序列，故变量序列LEC、LGDP、LGDP1、LGDP2、LGDP3 均为一阶单整序列。

2.3 变量间的协整性分析

尽管两个或两个以上的变量序列为非平稳时间序列，但它们的线性组合却可能呈现出稳定性，那么这两个变量之间便存在长期的稳定关系，即协整关系。ENGLE和GRANGER首先提出了变量之间的协整关系，并提出E－G两步法用于检验两个变量之间的协整关系。

(1)用普通最小二乘法估计变量之间的协整回归方程。笔者先估计能源消耗总量分别与国内生产总值、第一产业产值、第二产业产值和第三产业产值之间的协整回归方程，其估计结果如下:

(2)检验第(1)步得到的各协整回归方程中的残差序列的平稳性。经过ADF检验其残差序列若是平稳的，则说明变量之间存在协整关系;若是非平稳的，则说明变量之间不存在协整关系。经检验可得变量之间的协整关系如表2所示。

表2 各时间序列协整关系检验的结果

从协整分析结果可知，能源消耗总量与国内生产总值、第一产业产值、第二产业产值、第三产业产值均存在协整关系。且从以上协整方程式(1)～式(4)可得出能源消耗总量与国内生产总值及各产业产值之间的长期关系。由式(1)可知，国内生产总值LGDP每增长1%，能源消耗总量LEC增长0.180 220%;相应的，当LGDP1每增长1%时，LEC增长0.194 058%;LGDP2每增长1%，LEC增长0.202 446%;LGDP3每增长1%，LEC增长0.147 262%。可以看出，在三次产业增加值相同的情况下，第二产业耗费的能源量最多，而第三产业耗费的能源量最少。

2.4 变量间的误差修正模型

误差修正模型(error correction model，ECM)的基本形式是由DAVIDSON等于1978年提出的，该模型的分析也可称之为短期分析。由Granger定理可知，一组具有协整关系表达的向量一定具有误差修正模型的表达形式。因此，在协整检验的基础上，进一步建立变量间的误差修正模型，研究变量间的短期动态和长期均衡特征。笔者首先对能源消耗EC和国内生产总值GDP建立加入一阶滞后变量的误差修正模型:

由一阶误差修正模型式(5)可知，所有估计量均通过了T检验。且模型的拟合效果R2很高，DW=2.106 129距离2很近，说明各变量不存在自相关，故一阶误差修正模型合理。

由于具有一阶滞后项的标准分布形式为:

经恒等变形整理后可得:

该形式即为误差修正模型的标准形式，其中Yt－1－ β0/(1 － β3) － [(β1+ β2)/(1 － β3)]Xt－1若与协整回归方程式(1)相同，则它就是t－1时期的非均衡误差，即误差修正模型的修正项ecm。因此，变量Y的短期变化取决于变量X的短期变化和上一期的偏离均衡的程度，t时期Y的值对前期的非均衡程度做出了一定的修正。

一般地，误差修正模型可写成:

将式(5)能源消耗与经济整体发展水平之间的误差修正模型转化为标准形式，即:

在式(8)误差修正模型的标准形式中，0.610 956(LEC －6.560 146 －0.164 323LGDP)t－1为误差修正项，若t－1时刻LEC大于其长期均衡解6.560 146+0.164 323LGDP，则ecm为负，△LECt将减小;若 t－1时刻 LEC小于其长期均衡解6.560 146+0.164 323LGDP，则ecm为正，△LECt将增大。这符合反向修正机制，体现了如何将短期波动状态调整到长期均衡状态。误差修正项系数即能源消耗与国内生产总值的长期均衡对短期波动的调节系数为0.610 956，即当短期波动偏离长期均衡时，误差修正项以0.610 956的力度对短期波动进行调整，回到长期均衡状态。

同理，可得出能源消耗量与第一产业、第二产业、第三产业之间的误差修正模型，如式(9)～式(11)所示:

能源消耗总量与三次产业的短期内非均衡状态逐渐向长期均衡状态拉近的力度分别为0.764 980、0.537 718、0.553 717。

2.5 变量间的Granger因果关系检验

为进一步确定变量间的因果关系，需对变量间进行因果关系检验。一般地，变量X与Y之间的Granger因果关系检验，需要对以下两个回归模型进行估计。

无约束条件回归方程为:

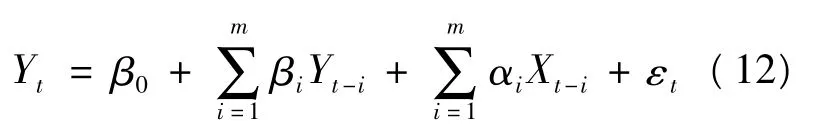
有约束条件回归方程为:

记式(12)的残差平方和为RSS1，式(13)的残差平方和为RSS0，构造F统计量为:

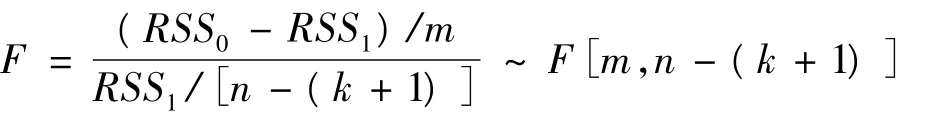
其中:n为样本观察值个数;k为式(12)中解释变量个数;m为X的滞后期数。F统计量服从F[m，n－(k+1)]分布。若F检验值大于标准F分布的临界值，说明X的变化是Y变化的原因。通过对天津市能源消耗量与产业发展水平的因果关系分析，可得如表3所示结果。

从表3可知，LEC不是LGDP的Granger原因的概率为0.147 1，即LEC是LGDP原因;而LGDP不是LEC的Granger原因的概率为0.975 0，说明能源消耗量LEC与国内生产总值LGDP之间存在单向Granger因果关系，能源的高消耗对经济增长具有一定的推动作用。LEC与LGDP1和LGDP3之间不存在显著的因果关系，说明第一产业和第三产业的发展与能源消耗之间不存在明显的因果关系。LEC与LGDP2之间存在单向Granger因果关系，LEC是LGDP2的原因，说明第二产业的发展与能源的高消耗密不可分。

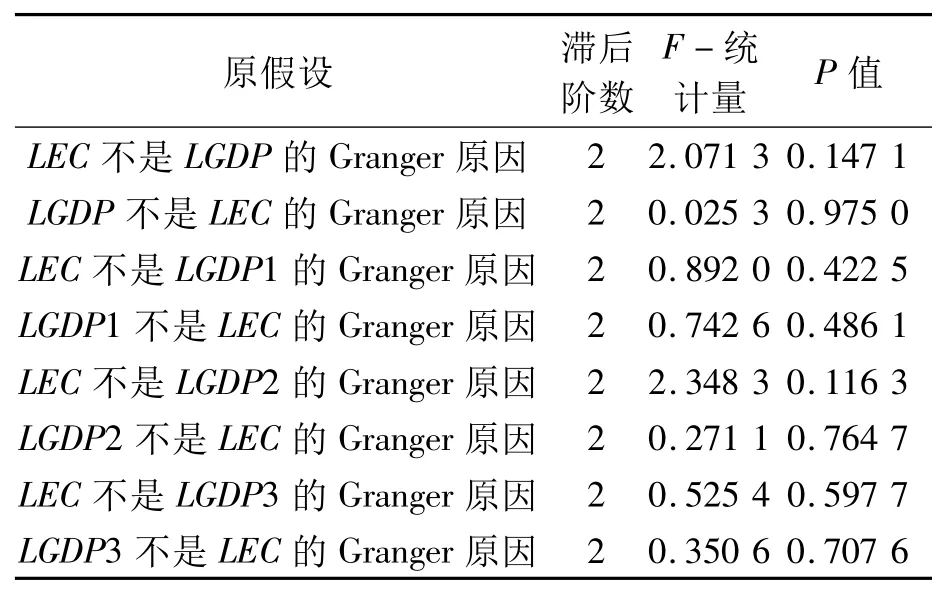
表3 天津市能源消耗量与产业发展水平的Granger因果关系检验结果

3 结论

通过协整分析可知，天津市整体经济发展水平和各产业发展水平均与能源消耗量之间存在长期稳定的均衡关系，即协整关系。由协整回归方程可知:第二产业对能源消耗的影响系数最大，其次为第一产业，而第三产业对能源消耗的影响系数最小。说明大力发展第三产业不会带来能源消耗的迅速增长，因此天津市应加大力度发展第三产业。通过因果关系检验可知，能源消耗量与经济发展水平之间存在单向Granger因果关系，而第一产业和第三产业与能源消耗之间的因果关系并不明显。第二产业与能源消耗之间只存在从能源消耗到经济增长的单向因果关系，即第二产业是能源依赖型产业。

天津作为我国北方最大的沿海工业城市，由于其特殊地理位置、资源禀赋和产业结构特点，第一产业在国民经济中所占比例很低，第二产业在国民经济中所占的比例始终保持在50%以上，远大于第三产业。2009年天津市第二产业的万元GDP能耗是第三产业万元GDP能耗的3.5倍。因此，“十二五”期间为进一步降低GDP能耗，天津市必须重视和挖掘其结构节能潜力，促进产业结构优化升级，发展科技含量高、附加值大、能耗小的新型工业。从资源密集型向技术密集型转变，逐渐减少高能耗产业的比例，提高能源使用效率，缓解经济增长对能源消耗的依赖。

[1] KRAFT J，KRAFT A.On the relationship between energy and GNP[J].Energy Development，1978(3):401 －403.

[2] YU E S H，CHOI J Y.The causal relationship between electricity and GNP:an international comparison[J].Journal of Energy and Development，1985(10):249 －272.

[3] MASIH A M，MASIH M R.On the temporal causal relationship between energy consumption，real income and prices:some new evidence from Asian－energy dependent NICs based on a multivariate cointegration vector error － correction approach[J].Policy Modeling，1997，19(4):417 －440.

[4] 林伯强.中国能源需求的经济计量分析[J].统计研究，2001(10):34－39.

[5] 韩智勇，魏一鸣，焦建玲，等.中国能源消耗与经济增长的协整性与因果关系分析[J].系统工程，2004，22(12):17 －21.

[6] 马宏伟，马开平.能源消耗与产业发展的协整性与因果关系分析[J].数理统计与管理，2010，29(3):473－479.

[7] 于全辉，孟卫东.基于面板数据的中国能源与经济增长关系[J].系统工程，2008，26(6):68 －72.

[8] 闫笑非，杜秀芳.中国能源消耗与产业结构变化关系的实证研究[J].改革与战略，2009，25(2):128 －131.

[9] 吴巧生，成金华.中国工业化进程中的能源消耗变动:基于计量模型的实证分析[J].中国工业经济，2005，205(4):30 －37.

[10] 白玉，章怀柯.资源型城市资源产业发展阶段的分析[J].武汉理工大学学报:信息与管理工程版，2010，32(3):450 －452.