利用粒子群算法计算AHP判断矩阵排序权重

张建华，李富萍

(1.中北大学电子与计算机科学技术学院，太原030051;2.太原科技大学计算机学院，太原030024)

层次分析法(AHP)是一种定性与定量相结合的多目标决策分析方法，它将人的主观判断为主的定性分析定量化，帮助人们在对复杂系统的思维过程中保持一致性[1-3]。在AHP中，如何合理地计算判断矩阵的排序权重是整个处理过程的关键，目前常用的计算方法大多使用近似算法，例如特征值法(EM)、最小偏差(LDM)、最小平方法(GLSM)等[4]。

根据判断矩阵的基本性质，可以将其排序权重计算归结为一个使一致性指标最小化的最小优化问题，文献[4]中提出检验判断矩阵一致性的遗传层次分析法(AGA-AHP)。AGA-AHP利用加速遗传算法，在检验判断矩阵的一致性的同时计算判断矩阵的排序权重，具有较高的求解精度[5]。因为遗传算法并不是一个连锁学习算法，在进化过程中，由于交叉和变异操作可能破坏构造块，从而影响计算结果的准确性。粒子群优化算法不存在连锁学习的问题，所以对于这类复杂的优化问题，粒子群优化算法更适合。

粒子群优化算法(Particle Swarm Optimization，PSO)是一种全局优化进化算法，该算法源于对鸟群捕食行为的研究。与遗传算法类似，PSO也是一种基于迭代的算法，它的基本思路是随机初始化一个群体(粒子群)，然后通过迭代过程对群体中各个个体(粒子)的速度和位置进行修正，直到算法结束。在PSO中，没有交叉和变异操作，群体中的粒子在迭代过程中追随解空间中的最优个体进行搜索，最终找到最优解。与遗传算法相比，不存在构造块破坏的问题，而且PSO更容易实现、需要调整的算法参数也很少[6-8]。

本文首先分析判断矩阵性质并对排序权重计算问题进行描述，接着介绍带惯性权重的粒子群优化算法，然后对判断矩阵排序权重计算进行讨论，最后给出仿真实验结果并对其进行分析。

1 排序权重计算

给定一个判断矩阵A=(aij)n×n，如果对应的排序权重为wk，k=1，2，…，n，那么wi＞0，且:

1)单位性，aii=wi/wi=1;

2)倒数性，aji=wj/wi=1/aij;

3)一致性，aijajk=(wi/wj)(wj/wk)=wi/wk=aik.

从以上性质可以得到:

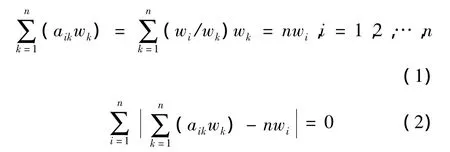
满足式(2)的判断矩阵是完全一致的。在实际应用当中，由于人的主观判断并不是完全精确的，并不能保证所有问题中的每个判断矩阵都具有完全一致性，只需要满足满意的一致性就可以接受。从式(2)可以看出，等号左边的值越小判断矩阵的一致性程度就越高。所以，判断矩阵的排序权重计算可以归结为一个由式(3)所描述的最小优化问题[1]:

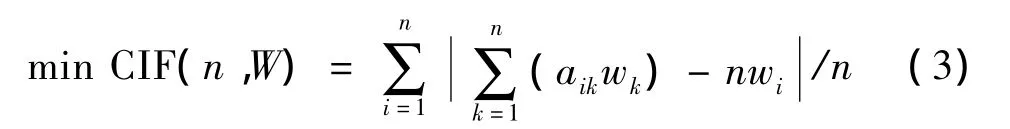
目前一般以判断矩阵阶数和判断矩阵最大特征值的差异程度作为度量判断矩阵一致性的指标。本文方法直接从判断矩阵的性质出发，更加直观合理。

2 带惯性权重的粒子群优化算法

用带惯性权重的粒子群优化算法处理式(3)所描述的最小优化问题。此算法在标准粒子群优化算法的基础上，通过改变惯性权重随进化过程的变化曲线来提高算法全局寻优性能[9]。

2.1 粒子群优化算法

在粒子群优化算法中，将每个个体看作在搜索空间中的一个粒子，各个粒子没有重量和体积，并在搜索空间中以一定的速度飞行。每个粒子的飞行速度根据自身的飞行经验和整个群体的飞行经验动态调整[9]。

设:

Xi=(xi1，xi2，…，xin):第i个粒子的位置;

Vi=(vi1，vi2，…，vin):第i个粒子的飞行速度;

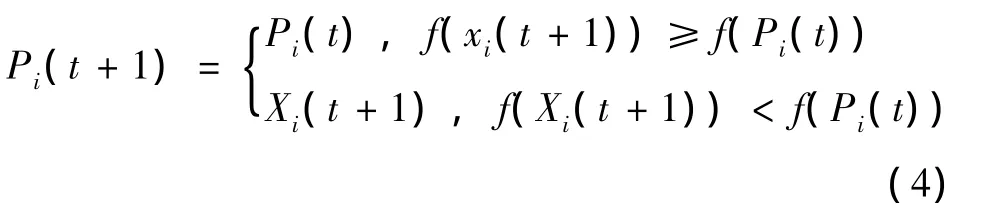
其中，f(X)为一个最小优化问题的目标函数。

假设群体中共有s个粒子，全局最优位置Pg(t)，也即群体中所有粒子所经历过的最好位置为:Pg(t)∈ {P0(t)，P1(t)，…，Ps(t)}|f(Pg(t))=min{f(P0(t))，f(P1(t))，…，f(Ps(t))}

式(5)和式(6)描述了基本粒子群优化算法的进化方程。

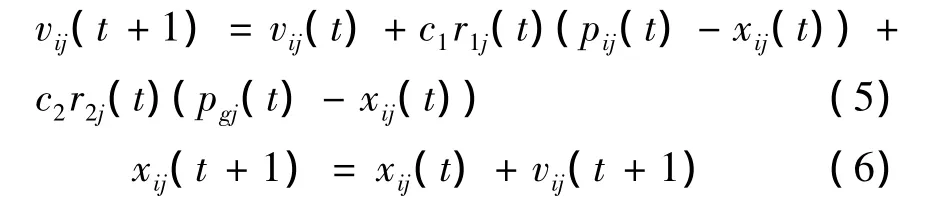
式(5)和式(6)中，t代表进化过程的迭代数，j代表粒子的第j维，i代表第i个粒子，c1、c2是在0～2之间取值的加速常数，r1～U(0，1)和r2～U(0，1)分别为两个相互独立的取值0到1之间的随机数。

从式(5)和式(6)的进化方程可以看出，c1的作用是调整粒子向其最优位置飞行的步长，c2用来调整粒子飞向全局最优位置的步长。vij∈[－vmax，vmax]，其中vmax=k·xmax，0.1 ≤k≤ 1.0，[－xmax，xmax]是问题的搜索空间。限制vij的取值范围是为了降低粒子在进化过程中飞离搜索空间的可能性。

1998年，Shi Y和Eberhart R C在基本粒子群优化算法基础上，引入惯性权重到速度进化方程中[10]，用来改善基本 PSO算法的收敛性能，如式(7)所示。

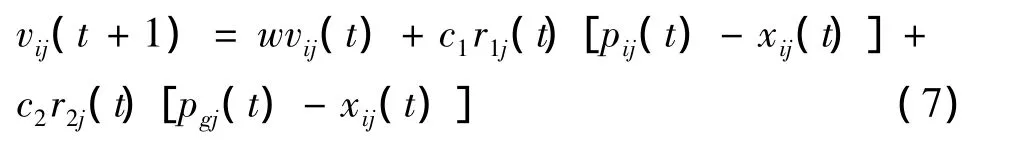
式(7)中w称为惯性权重。惯性权重w使粒子的运动保持一定的惯性，使粒子能够探索搜索空间中的新区域。

因为惯性权重w本身具有平衡全局和局部搜索能力的作用，所以引入惯性权重w可以去除基本

Pi=(pi1，pi2，…，pin):第i个粒子飞行路径上的最好位置，即粒子i飞行路径上，适应值最好的位置，称这个位置为个体最优位置。对于最小优化问题，如果一个位置的目标函数值越小，那么该位置的适应值就越好。

粒子i的当前最优位置可用式(4)确定:PSO算法对vmax的限制。当vmax增加时，可以通过减小w来平衡搜索过程，而减小w又可以减少进化过程的迭代次数。这样，可以将各维变量的变化范围作为vmax的取值范围，通过对w的调节达到相同的目的。

目前，PSO算法的相关研究大部分是在带惯性权重PSO算法的基础上进行扩展和修正，在很多文献中将带惯性权重PSO算法称为PSO算法的标准版本，简称为标准PSO算法，而基本的PSO算法被称为PSO的初始版本[9]。可以看出，当惯性权重w=1时就是PSO算法的初始版本。

2.2 改进全局寻优性能

为了改进算法的全局寻优性能，一个好的方法是在进化前期提高群体的多样性，从而得到合适的种子，在进化后期提高算法局部寻优性能以提高计算精度。惯性权重w类似于模拟退火算法中的温度参数，如果希望算法全局寻优能力强，那么w应取较大的值;如果希望算法具有较强的局部寻优能力，应当选择较小的w.一般来说，在进化算法的迭代初期应当使探索范围尽量的大，也就是强调全局寻优能力;在进化迭代的后期为了提高寻优的精度，要求算法在此阶段应该具有较好的局部寻优能力。从这个角度来看，惯性权重w应该随迭代次数的增加不断地减少。在文献[7]中，惯性权重w用式(8)来计算:

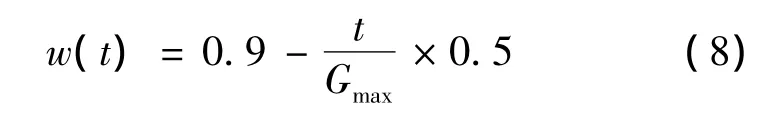
其中，Gmax是最大进化迭代次数，根据当前的进化迭代数确定惯性权重w[11].

本文算法中采用式(8)计算惯性权重。

2.3 完整PSO算法描述

1)为群体中的各个粒子设定随机位置和速度进行初始值;

2)为群体中各个粒子计算适应值;

3)对群体中各个粒子，根据式(4)，确定它的当前最优位置;

4)设置当前的全局最优位置Pg为所有粒子中具有最优适应值的粒子位置;

5)对群体中各个粒子，利用式(7)和式(6)计算其速度和位置;

6)如果未达到算法结束条件，转到2);否则结束算法。

3 判断矩阵排序权重计算算法描述

下面给出用于解决式(3)所描述的最小优化问题的算法PSO-AHP.

1)给定一个判断矩阵A=(aij)n×n，初始化N个向量为种群规模各分量为[0，d]上的均匀随机数，d是一个常数，用来控制各权重的上限，取2，…，N为第一代群体;初始化N个对应的速度向量各分量为[－vmax，vmax]上均匀随机数，算法中vmax=0.1，控制粒子一次迭代中最大的速度变化值;

3)对群体中的各个粒子，与Wi的适应值做比较，当前最优位置Wi设置为其中最好适应值对应的位置;

4)比较全局最好位置Wg以及上一步得到的Wi，i=1，2，…，N的适应值，选择其中具有最好适应值的Wi作为当前全局最优位置Wg;

5)对群体中的各个粒子，利用式(7)和式(6)计算得到下一次迭代的

6)如果未达到算法结束条件，转到2);否则转到7);

7)输出排序权重Wg=(w1，w2，…，wn)以及一致性指标CI=CIF(n，wg).

4 仿真实验结果及分析

4.1 仿真实验结果

仿真实验中，使用EM方法和PSO-AHP算法计算下列两个判断矩阵B1和B2.

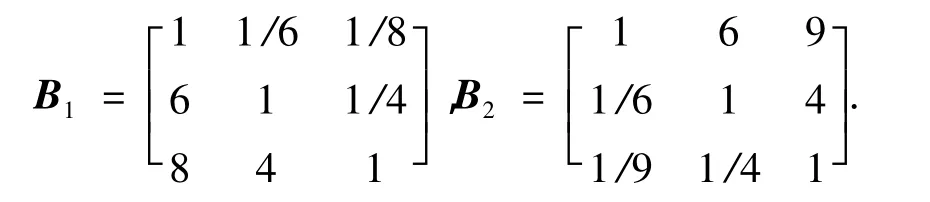
仿真实验结果如表1所示。

从表1可以看出，对于判断矩阵B1和B2，EM方法的计算结果表示它们是不一致的，但是PSOAHP计算却得到一致的结论，而且一致性指标较好。在AHP中，如果一个判断矩阵不一致，一般的做法是要求决策者重新考虑其决策数据，使判断矩阵满足一致性指标然后再进行计算。如果给决策者提供了错误的一致性信息，决策者就不得不对已经做出的正确决策进行改动，导致决策上的误差。PSO-AHP给出准确的一致性指标能够避免这种情况发生。

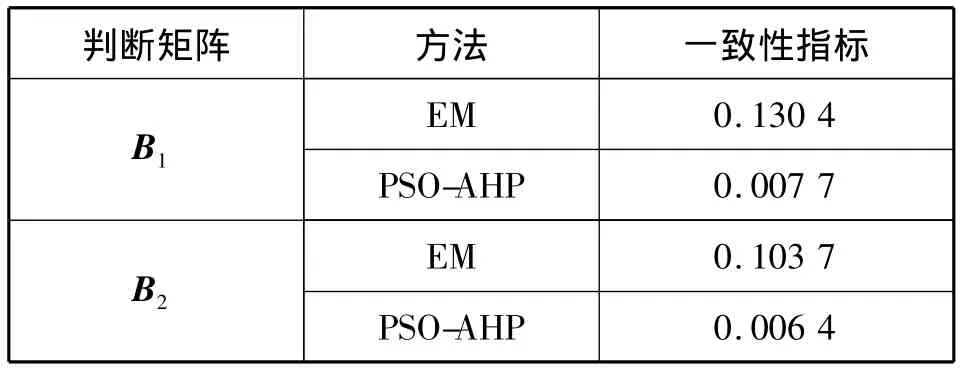
表1 仿真实验结果Tab.1 The simulation results

4.2 与其他方法的仿真实验计算结果对比

为了与其他算法的计算结果进行比较，用下面三个判断矩阵进行仿真实验，其中判断矩阵B3具有完全一致性。

仿真实验参数:种群规模:B3∶75，B4/B5∶150;最大代数:100.

表2是本文算法与其他几种算法的仿真实验结果比较，EM、LDM、GLSM以及AGA-AHP的数据来源于文献[1]。与其他几种算法相比，本文算法的精度最高。

表3是使用PSO-AHP进行100次独立仿真实验的统计数据。从表3可以看出，统计数据的均值和方差很小，说明算法的稳定性很好。

5 结论

根据判断矩阵的基本性质，计算判断矩阵的排序权重可以转换为寻找最小的判断矩阵一致性指标所对应的各指标权重。本文采用改进的粒子群优化算法对这个优化问题进行处理，通过算法的进化迭代能够找到一致性指标的全局最优，全局最优一致性指标对应的粒子位置即为判断矩阵的排序权重。从仿真实验结果可以看出，本文所描述的算法具有很高的精度，并且算法的稳定性也很好。

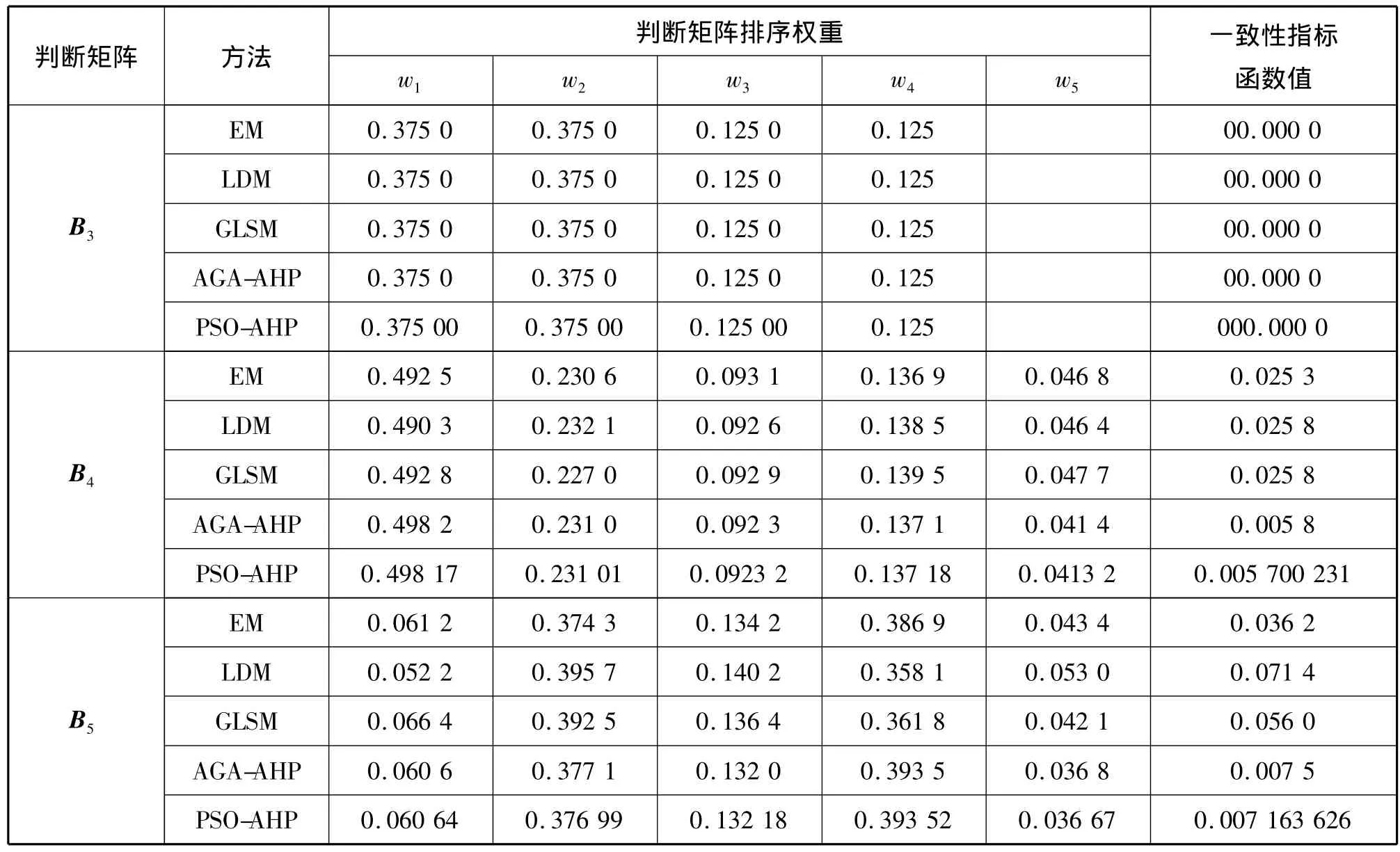
表2 与其他方法的计算结果比较Tab.2 Comparison with other algorithms

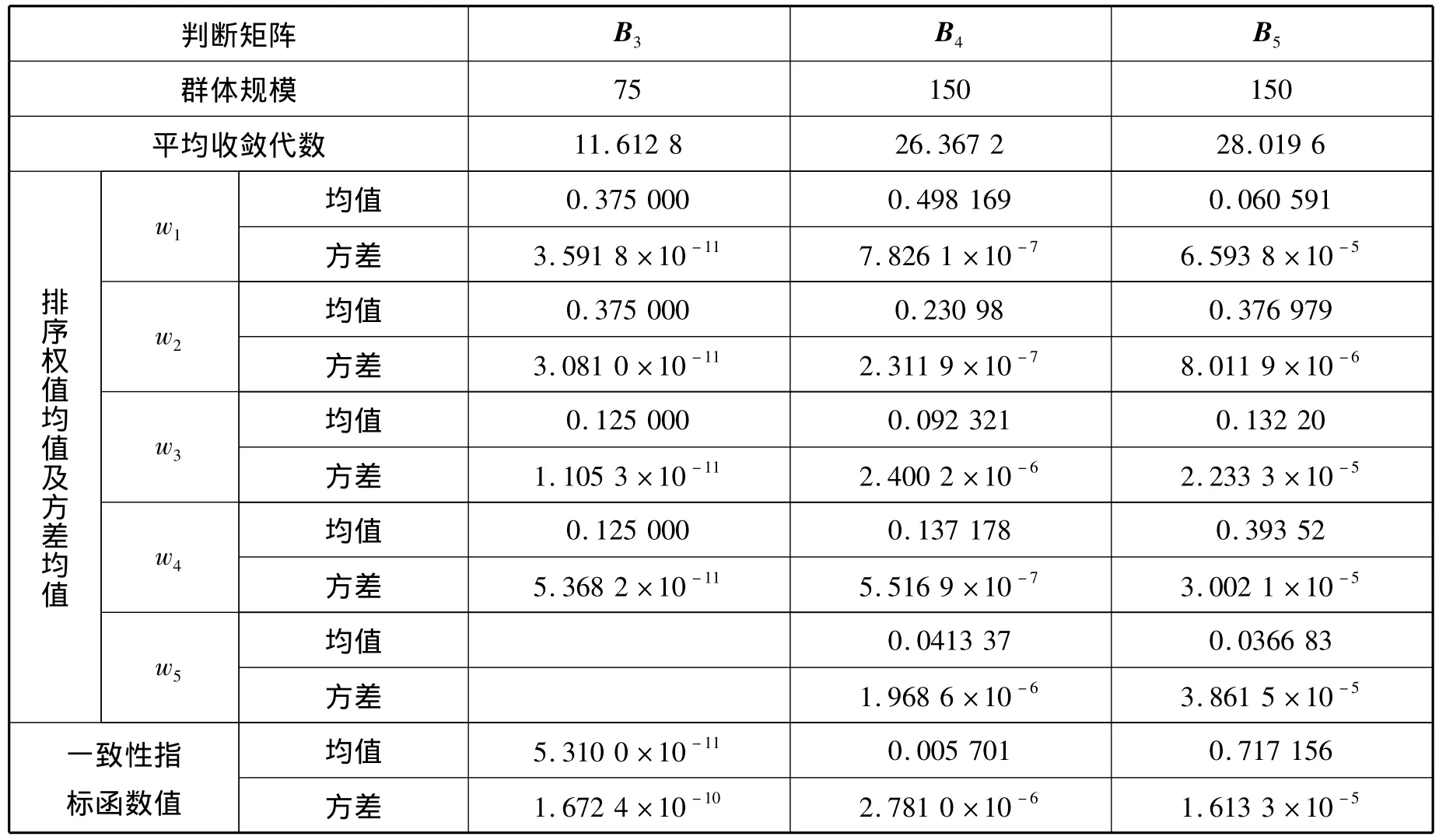
表3 100次实验测试结果Tab.3 The results of 100 experiments

[1]金菊良，魏一鸣.复杂系统广义智能评价方法与应用[M].北京:科学出版社，2008.

[2]SAATY T L.How to make a decision，The analytic hierarchy process[J].European Journal of Operational Research，1990，48:9-26.

[3]ZIA M J，AZAM F，ALLAUDDIN M.A Survey of Enterprise Architecture Analysis Using Multi Criteria Decision Making Models(MCDM)[J].Intelligent Computing and Information Science，2011，135:631-637.

[4]徐泽水.层次分析中判断矩阵排序的新方法——广义最小平方法[J].系统工程理论与实践，1998，18:38-43.

[5]金菊良，魏一鸣，付强.计算层次分析法中排序权值的加速遗传算法[J].系统工程理论与实践，2002，22:39-43.

[6]王小平，曹立明.遗传算法理论、应用与软件实现[M].西安:西安交通大学出版社，2002.

[7]ADLEMAN L M.Molecular Computation of Solutions to Combinatorial Problems[J].Science，1994，266(5187):1021-1024.

[8]SRINIVASAN，D，LOO W H，CHEU R L.Traffic incident detection using particle swarm optimization[C]∥2003 IEEE，Swarm Intelligence Symposium，2003:144-151.

[9]曾建潮，介婧，崔志华.微粒群算法[M].北京:科学出版社，2004.

[10]SHI Y，EBERHART R C.A modified particle swarm optimizer[C]∥IEEE World Congress on Computational Intelligence，Piscataway，NJ，IEEE Press，1998:69-73.

[11]SHI Y，EBERHART R C.Empirical study of particle swarm optimization[C]∥1999 Congress on Evolutionary Computation，Piscataway，NJ，IEEE Service Center.1999:1945-1950.