一种非最小相位系统控制方法

孟 香

(太原科技大学团委，太原030024)

非最小相位系统是控制工程中常见的一类对象[1-3]，由于传递函数存在负零点，非最小相位系统的阶跃响应存在负调，其负调形式和负零点的个数相关[3]:若系统存在奇数个负零点，则系统的阶跃响应首先将走向设定值的反方面再返回;若存在偶数个负零点，则系统的阶跃响应在跟随设定值方向一段时间后再走向设定值的反方面然后返回。

对于非最小相位系统的控制，存在的难题是负调幅值和调节时间存在耦合关系[4]，即抑制负调幅值会延长调节时间，采用常规的线性控制器很难折衷两者之间的竞争关系。对于这类对象的控制，先后曾采用过不同的控制方法，如:二自由度控制[5]、预测控制[6]、滑模控制[7]等。近年来，一些文献提出了基于智能控制技术的非最小相位系统控制方法[8-10]，取得了一定的效果。这些方法在工程实施中或多或少存在一定的不足。

本文采用一种非线性控制方法对非最小相位系统进行控制。利用文献[11]中所提的电容结构形式构造非线性控制器。该控制器在状态空间上旋转，并使旋转角和系统误差状态相关联，这一方法可以非常简洁、有效地控制非最小相位系统。

1 控制方法

利用电容极间电场作用和控制作用的相似性，构造一种非线性函数[11]:

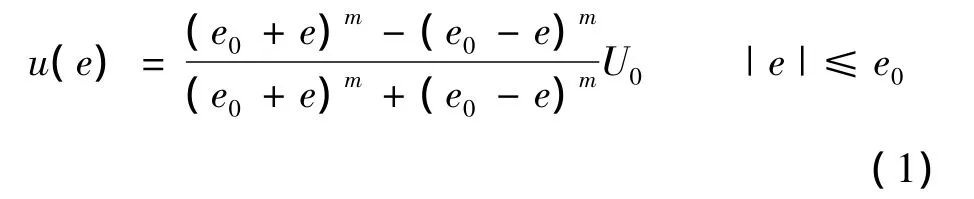
式(1)中:参数e0表示电容两极间距，用来限定控制范围，当|e|＞e0时，则采用截取方式e=e0·sign(e)进行处理;U0表示电容两极的电压，用来调整控制量幅值;参数m用来调整非线性函数的特征，当m=1时，式(1)为线性函数。

利用函数式(1)对常规PID控制器进行修正，即可形成一种非线性控制器:

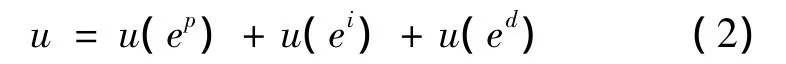
式(2)由独立的三个项组成:ep为控制误差、ei为控制误差的积分、ed为控制误差速率，每一项都采用式(1)的函数结构形式，因此，式(2)包括9个调试参数。为了减少参数个数，考虑上述电容结构在状态空间(如相平面)上旋转，使电容结构的作用分配到各状态轴上(如图1)，则调试参数可以大为减少。

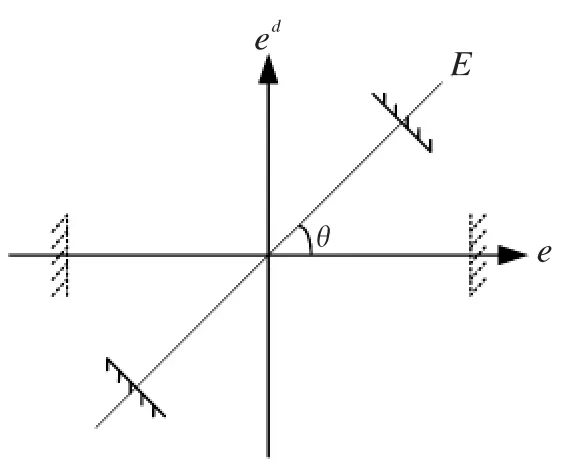
图1 电容结构在相平面上的旋转Fig.1 Rotation of capacitance structure on the phase plane

在图1的相平面中，假设电容结构旋转θ角，则e轴和E轴的状态对应关系为:

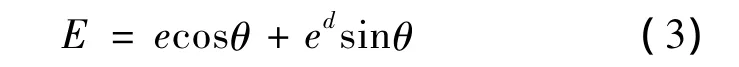
将式(3)代入式(1)得:

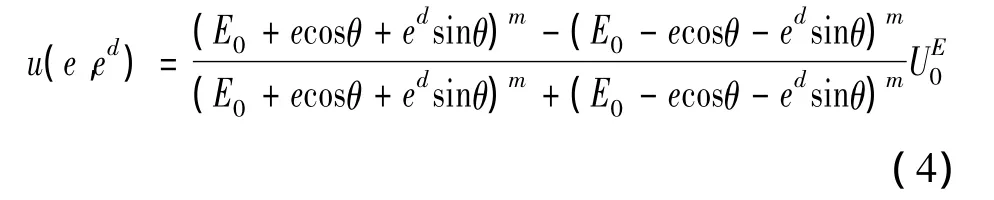
式(4)中，E0=ep0cosθ+ed0sinθ、ep0和ed0是各状态量最大值，UE0=U0×E0为电容结构的电压值。显然，式(4)是一个非线性PD控制器，它通过一个电容结构对状态量e、ed同时提供约束，使控制参数大为减少。同样，若状态量选择为e、ei，则电容结构形成一种非线性PI控制器。

式(4)中，旋转角θ可以按照控制调试的经验准则来确定:当系统误差较大，控制系统主要考虑的是尽快减小误差，而对系统稳定性的考虑可以适当放宽，这时应加大系统的控制量;而当系统误差较小时，控制在误差归零之前的一段时间，应提前加入制动的控制量以防止系统超调。

按照这一思想可以建立如下的旋转角θ和误差状态的联系:

实际上，式(5)是将系统的控制误差e映射为图1中的旋转角θ，其中，θmin为最小误差emin所对应的旋转角;θmax为最大误差emax所对应的旋转角，emin通常为0，emax为最大误差。

在参数调试时，通常emax根据实际设备情况将emax固定为一个值，emax不需要很精确，只要保证系统大部分的误差状态e小于emax即可。若e＞emax，则采用如下的截断处理:

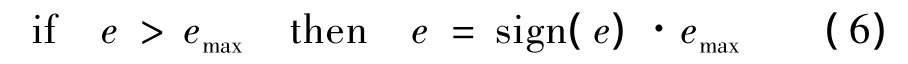
系统的控制性能主要通过θmax、θmin的调试来确定。

对于非最小相位系统的控制器设计，文献[4]提出一种通过改变负零点个数，进而改变负调类型的方法来抑制负调幅值。这一方法可以很方便地利用旋转电容结构来实现:当旋转角θ＜0时，显然，电容结构提供一个负零点;而当θ＞0时，电容结构提供正零点。可见，利用旋转角θ的变化，电容结构可以给出适合非最小相位系统所需的控制率。

2 仿真示例

下面通过仿真测试本文所提方法的控制性能，仿真对象为文献[12]所给出的水轮机系统，其传递函数为:

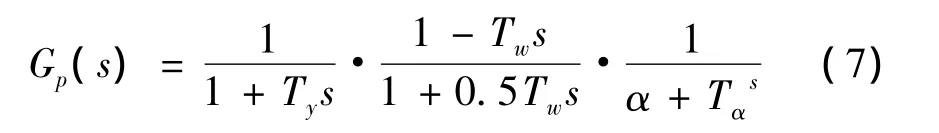
式中:Ty为接力器缓冲时间常数，Tw为水流惯性时间常数，Tα为发电机惯性时间常数，α为发电机负荷自调整系数。

显然，上述水轮机系统是一个典型的非最小相位系统，具有奇数个负零点。

令水轮机系统模型式(7)中的参数[12]为:Ty=0、Tw=0.8、α=0.2、Tα=0.96，利用遗传算法和模拟退火形成一种混合控制策略[12]，整定得到如下的PID控制参数:

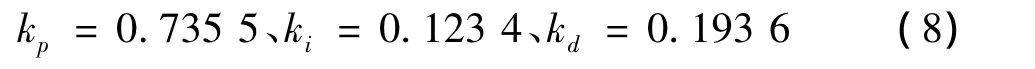
下面给出电容结构的控制效果。先不考虑电容结构的旋转，利用式(1)对线性控制器(8)进行非线性修正，按照文献[11]，式(1)的参数选择在线性PID的控制参数(8)的基础上进行微调。通过仿真，参数选择如下:

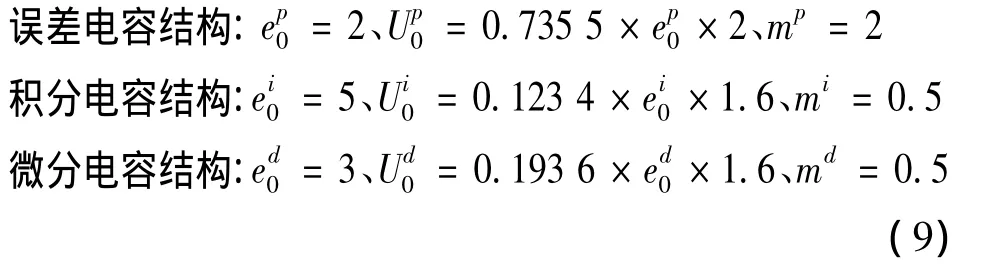
上述参数中，e0、U0、m分别为对应维的电极间距、电压以及非线性特征参数。其中，参数e0取一个估算值即可，参数m根据控制所需的非线性特点来选定，随着m的不同，参数U0需要作相应的调整。式(9)的控制效果见图2，相应的控制指标:在线性PID控制下，单位阶跃响应的负调值约为－0.41，而电容结构 PID控制下的负调值约为－0.263;两者的超调量相同，其峰值均为1.04;线性PID的调节时间约为5.5 s，而电容结构PID调节时间约为6 s.

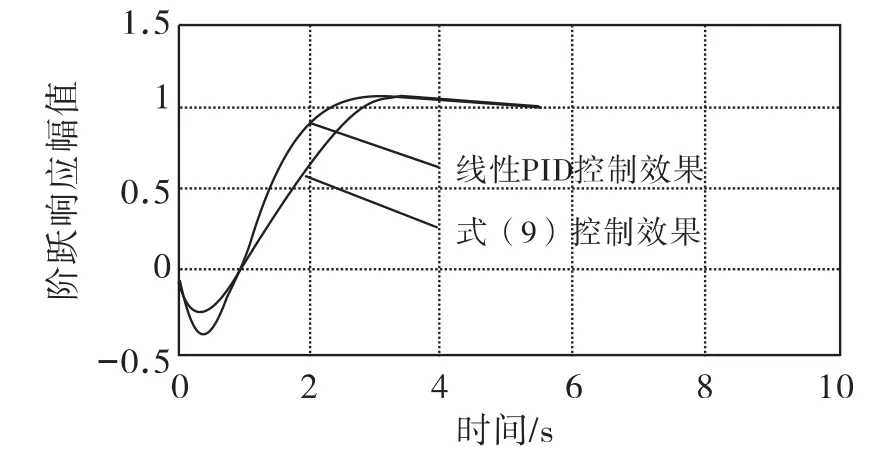
图2 基本形式的电容结构的控制效果Fig.2 Control effect on the basic form of capacitance structure

从总的效果来看，电容结构PID的控制效果要比线性PID的控制效果略好些。

进一步考虑旋转电容结构。将式(9)中的误差电容结构和微分电容结构合并为旋转电容结构，积分电容结构仍保持为单独的结构。旋转电容结构的状态量、控制作用分别为式(3)、(4)，旋转角和状态量的对应关系取为式(5)。

在式(9)的基础上，旋转电容结构的参数选择为:

旋转电容结构:

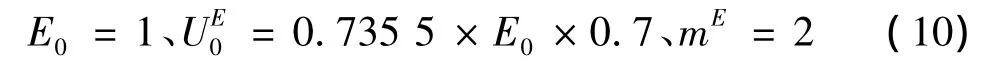
这里，为了限制旋转电容结构输出的控制量，对电极间距参数E0进行了截取处理。

旋转角和状态的对应关系按如下确定:由于在负调阶段，误差e大于设定值，因此取emin=0、emax=r，r为设定值;对应的旋转角为θmin=0、θmax通过调试确定为24°，采用式(5)计算旋转角，在负调阶段有θ＜0，而在其它时段有θ＞0.可见，电容结构的旋转能够方便地实现文献[4]所提出的通过改变负零点个数从而抑制负调的方法。

积分电容结构不参与旋转，可通过调试其参数重新选择。

积分电容结构:

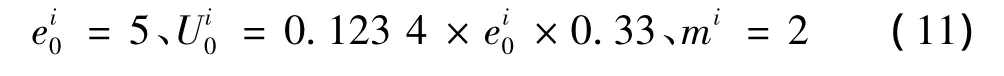
旋转电容结构的控制效果如图3所示，其具体的控制指标如下:阶跃响应的负调幅值为－0.18，超调幅值为1.02，调节时间约为5 s.

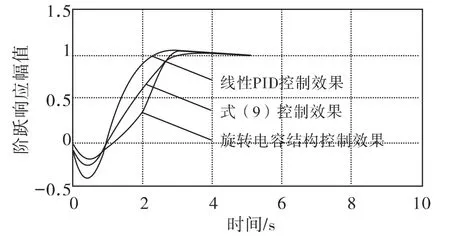
图3 旋转电容结构的控制效果Fig.3 Control effect on the rotating capacitance structure

电容旋转结构可以通过简单的旋转角度的调整来适应非最小相位系统的控制要求，因此，其控制效果要比非线性控制式(9)的效果要好。

4 结论

本文采用一种非线性控制方法对非最小相位系统的控制进行了讨论。利用电容电场作用和控制作用的相似性构造一种非线性函数，进而利用这一函数对线性PID控制器进行非线性修正;利用电容结构在空间的旋转形成一种适合非最小相位系统的控制方法。通过仿真表明，所提的控制方法非常灵活，可以根据被控对象的特性需要构造针对性的控制策略，并且其参数调试和常规PID控制相似，易于在工程中使用。

[1]ASTROM K，HAGGLUND T.PID Controllers:Theory，Design and Tuning[M].New York:ISA，1995.

[2]刘乐星，毛宗源.水轮机的GA2PID控制器研究[J].电力系统自动化，1997，21(12):41-43.

[3]王凌，李文峰，郑大钟.非最小相位系统控制器的优化设计[J].自动化学报，2003，29(1):135-140.

[4]何真，陆宇平，郑成军.一种新的非最小相位系统得控制方法[J].信息与控制，2006，35(5):561-563.

[5]王维杰，李东海，高琪瑞，等.一种二自由度PID控制器参数整定方法[J].清华大学学报:自然科学版，2008，48(11):1962-1966.

[6]孙建平，李晓燕，王立军，王俊.广义内模预测控制在非最小相位系统中的应用[J].电力科学与工程，2009，25(8):41-44.

[7]祝萌，吴晓男，于进勇.一种非最小相位导弹过载控制系统设计方法研究[J].弹箭与制导学报，2010，30(1):47-50.

[8]李东海，吴麒.非最小相位系统得智能控制方法[J].控制与决策，1996，11(6):633-637.

[9]LI T，SHIEH M.Design of a GA based fuzzy PID controller for non-minimum phase systems[J].Fuzzy Sets and Systems，2000，111(2):183-197.

[10]PARK S，PARK L，PARK C H.A neuro-genetic controller for non-minimum phase systems[J].IEEE Transactions on Neural Networks，1995，6(5):1297-1300.

[11]尚宏，陈志敏，任永平.一种新型非线性PID控制器及其参数设计[J].控制理论与应用，2009，26(4):439-442.

[12]李清生，王陵，郑大钟.水轮机系统的控制器整定研究[J].基础自动化，2001，8(3):10-12.