时滞不确定系统的支持向量机滑模控制

赵 倩，陈志梅，张井岗

(太原科技大学电子信息工程学院，太原030024)

在实际控制系统中普遍存在着时滞现象，而时滞的存在使得系统的控制品质变差，甚至会导致系统的不稳定，因此对时滞系统的控制成了控制领域的研究热点。现在处理时滞系统的方法主要有基于Riccati方程设计鲁棒控制器的方法、Smith预估策略、输出跟踪控制方法、LQR/LTR算法等[1-4]。变结构控制由于它的突出优点即滑动模态对系统内部参数变化及外界扰动具有不敏感性，为不确定性系统、非线性、时滞、时变及干扰源多的一类系统的鲁棒性设计提供了一种有效途径[5]。然而，其固有的抖振现象以及由于系统参数变化、外部干扰以及未建模动态等因素的影响，使得其要求的条件往往难以满足，限制了滑模控制的应用，因此与其它的理论与方法相结合成为滑模控制研究的一大发展趋势[6-7]。

神经网络作为一种通用函数逼近器，可以以任意精度近似任意非线性函数和动态系统，在针对不确定系统时，一般采用神经网络对不确定性上界进行自适应学习[8]。然而，神经网络仍有一些不易解决的难题，如难以确定神经网络的隐层节点数、存在过学习现象、训练过程中存在局部极小问题等。为了解决这些问题，Vapnik提出支持向量机(Support Vector Machine，SVM)即一种依据统计学习理论和结构风险最小化原理的新型学习机[9]。与神经网络相比，它的优点是训练算法中不存在局部极小问题，可以自动设计模型复杂度(例如隐层节点数)，不存在维数灾问题，泛化能力强，已在模式识别、信号处理、函数逼近等领域得到了应用[10]。

本文针对具有不确定参数和状态时滞的系统，基于LMI方法设计滑模控制器，引入支持向量机对不确定量在线逼近，通过学习获得其上界值，保证了系统的稳定性和强鲁棒性，有效地降低滑模控制固有的抖振现象，改善了系统的控制性能。

1 系统描述

考虑如下带有不确定性参数的时滞系统:

其中，x∈Rn为状态输入，u(t)∈Rm为控制输入，ξ(x，t)为系统所受的外部干扰，φ(t)∈Rn为连续的初值函数，而A、Ad和B为已知的具有合适维数的常值矩阵，常值时滞τ≥0，△A、△Ad和△B为系统的不确定性。对于系统式(1)作如下假设:

(i)假设系统的不确定性和外部干扰满足标准匹配条件，即存在有界矩阵和满足和

(ii)矩阵对(A+Ad，B)是可控的。

根据以上假设，系统式(1)可以描述成:

其中δ(x，t)为系统总的不确定性

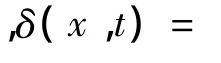
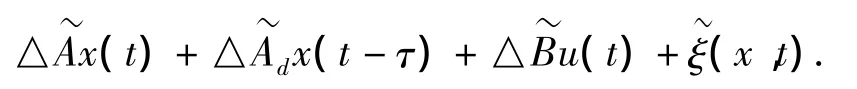
2 滑模控制器设计

引入如下的变换将系统式(2)转换为标准形式z=Tx，其中，T满足条件:

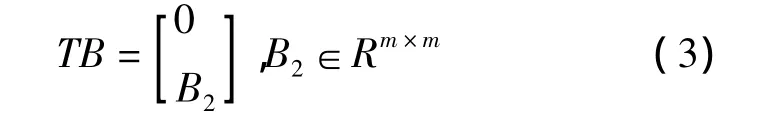
则可得:

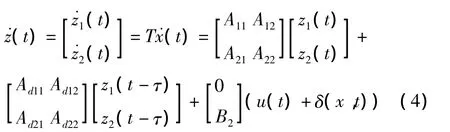
定义滑模函数

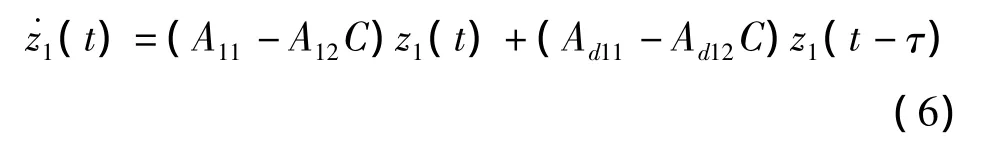
则:若存在正定对称矩阵Q∈R(n－m)×(n－m)、矩阵Y∈Rm×(n－m)和正实数^τ满足如下线性不等式(*是矩阵的对称块的转置):

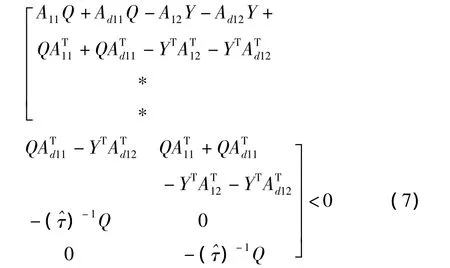
那么选择待定参数矩阵为C和C=YQ－1，则对所有满足0≤τ≤^τ的常值时滞τ，系统的滑动模态式(6)是渐进稳定的[11]。

对时滞系统式(4)，其滑模面由式(5)定义，则在控制律

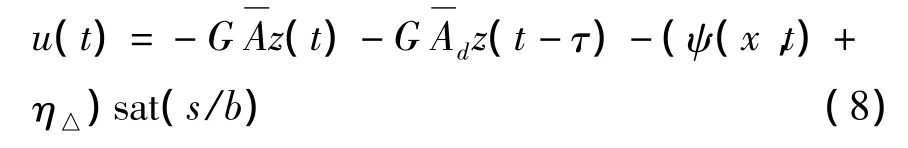
作用下，系统轨迹将在有限时间内到达滑模面并沿着滑模面运动。其中，η△＞0是标量，用于调整滑模面的趋近速度，ψ(x，t)为δ(x，t)的上界值[11]。

3 支持向量机学习不确定部分

式(8)中不确定性δ(x，t)的上界值ψ(x，t)假定已知，但在实际情况中，对于系统的不确定部分很难测量或者根本无法测量，因此控制律无法求取。本文引入支持向量机对未知的不确定部分进行自适应学习，利用支持向量机模型的输出代替不确定性。在具体对不确定部分进行学习时，首先利用输入变量和输出变量的样本对支持向量机进行训练，然后利用训练好的模型对输出变量进行估计。最后在非线性系统模型中，输入变量与输出变量之间的非线性函数关系由支持向量机的输出来实现[12]。具体的学习过程为:

设样本为n维向量，某区域的l个样本及其值表示(x1，y1)，…，(xl，yl)∈Rn×R，首先用一非线性映射ψ(·)把样本空间Rn从原空间映射到特征空间ψ(x)=(φ(x1)，φ(x2)，…，φ(xl)).在这个高维特征空间中构造最优决策函数y(x)=ω·φ(x)+b，这样非线性估计函数转换为高维特征空间中的线性估计函数。利用结构风险最小化原则，寻找ω，b，就是最小化，其中‖ω‖2是控制模型的复杂度，c是正规化参数，Remp为误差控制函数，即ε不敏感损失函数。

支持向量机估计算法的优化问题为:

建立Lagrange函数:

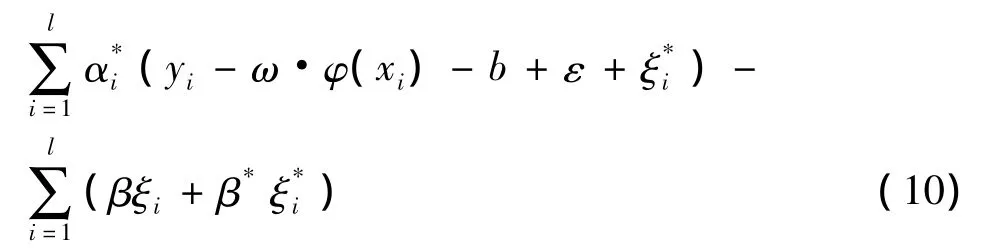
根据优化条件:

根据 Mercer’s条件，定义核k(xi，xj)=φ(xi)·φ(xj).则优化问题转化为:

选取核函数为径向基核函数:k(xi，xj)=exp(－‖xi－yj‖2/2σ2)。参数b用KKT条件可以求出:

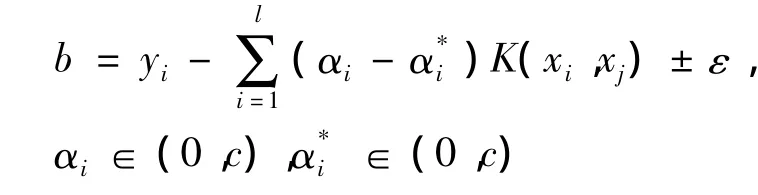
则支持向量机的输出为:

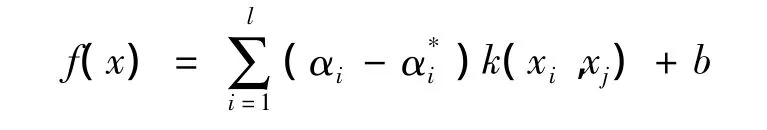
4 仿真研究

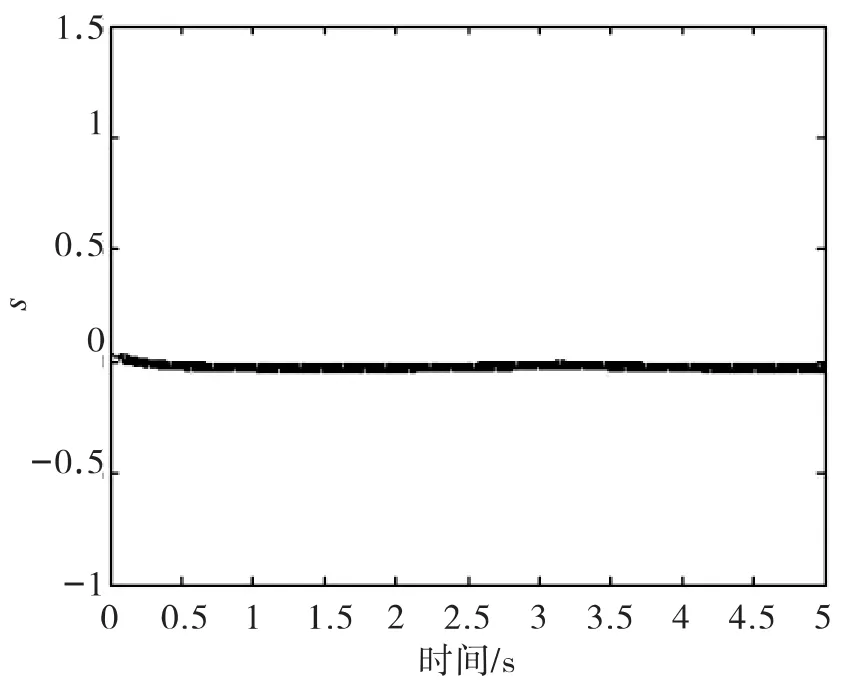
图1 滑模函数曲线Fig.1 Sliding mode function curve

图2 上界值假定已知的滑模控制器输出曲线Fig.2 SMC output curve based on assumed upper bound

图3 利用支持向量机学习的上界变化曲线Fig.3 Upper bound learned curve based on SVM

图1、图2为假定上界值为0.8时，滑模函数以及滑模控制器输出曲线;图3为利用支持向量机学习未知不确定部分上界值的变化情况;图4为采用基于SVM的滑模控制器输出曲线;图5和图6为系统状态响应曲线。

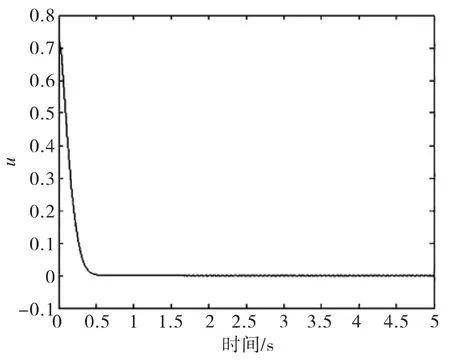
图4 基于SVM的滑模控制器输出曲线Fig.4 SMC output curve based on SVM

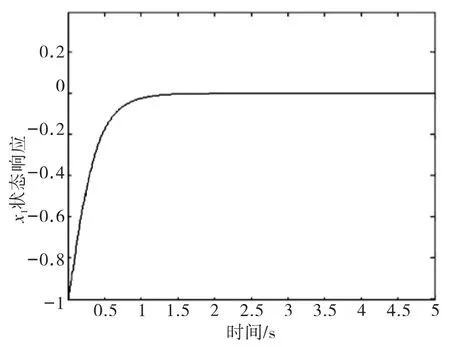
图5 x1状态响应曲线Fig.5 State response curve of x1

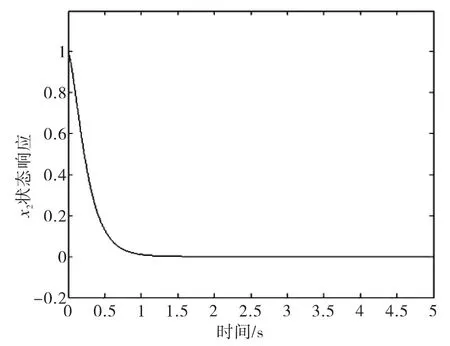
图6 x2状态响应曲线Fig.6 State response curve of x2

从仿真结果可以看出，系统状态在有限的时间内能够达到滑模面，采用基于SVM的滑模控制不仅能够获得不确定部分的上界值，同时有效地抑制了抖振，保证系统状态的渐近稳定性和鲁棒性。

5 结论

本文针对一类具有状态时滞的不确定系统，应用滑模控制理论，基于LMI方法设计了控制器，利用支持向量机自学习不确定部分未知上界。该方案克服了滑模控制需要已知系统不确定性上界的限制，同时保证了系统的渐近稳定性和鲁棒性，有效地削弱了抖振，提高了系统的性能。

[1]EL-KHEZALI R，AHMAD W H.Variable structure control of fractional time-delay systems[C]//2nd IFAC，Workshop on fractional differentiation and applications，Porto，Portugal，2006.

[2]AMAR SI-AMMOUR，SAID DJENNOUNE.A sliding mode control for linear fractional systems with input and state delays[C]//Maamar Bettayeb Commun Nonlinear Sci Numer Simulat，2009，14:2310-2318.

[3]张静梅，贾新春.不确定时变时滞线性系统的鲁棒采样控制[J].太原科技大学学报，2009，30(4):302-308.

[4]HE Y，LIU G P，REES D，M.W.H∞filtering for discrete-time systems with time-varying delay[J].Signal Processing，2009，89(3):275-282.

[5]EFE M O，UNSAL C，KAYNAK O，et al.Variable structure control of a class of uncertain systems[J].Automatica，2004，40:59-64.

[6]范志勇，张井岗.“倒三角”系统的神经滑模控制[J].太原科技大学学报，2010，31(4):271-274.

[7]WINSTON GARCIA-GABIN，DARINE ZAMBRANO，EDUARDO F.Camacho.Sliding mode predictive control of a solar air-conditioning plant[J].Control Engineering Practice，2009，17:652-663.

[8]高宏宇，邵克勇，李艳辉.不确定系统的上界自适应动态神经滑模控制[J].吉林大学学报:自然科学版，2010，28(3):292-297.

[9]VAPNIK V N.Statistical learning theory[M].New York:John Wiley and Sons Inc，1998

[10]ZHONG W M，PI D Y，SUN Y X.An Approach of Nonlinear Model Multi-step-ahead Predictive Control Based on SVM[J].Lecture Notes in Computer Science，2005，35(16):1036-1039.

[11]苏宏业，褚健，鲁仁全，等.不确定时滞系统的鲁棒控制理论[M].北京:科学出版社，2007.

[12]张明光，阎威武，李战明.基于支持向量机的非线性系统辨识研究[J].计算机应用研究，2006(5):47-48.