采用孔隙体积法计算平均毛管压力曲线

郭晓博

(大庆油田有限责任公司 勘探开发研究院，黑龙江 大庆，163712)

根据油气成藏理论，油气藏形成是由于毛管压力充当动力，使烃源岩中生成的油气逐渐驱替原始地层中的水，随着油气聚集程度提高，逐渐达到毛管力、浮力、重力之间的平衡。根据这个理论，假设油藏在开钻第1口井之前，油藏内外温度恒定，毛管压力、浮力、重力处于静态平衡状态(将砂岩定义为多孔隙结构体，没有等效为毛管束)，从自由能出发，用热动力学证明了毛管力与浮力、重力相互关系式，通过未固结砂岩的实验，对所有干净的未固结砂岩，Leverelt[1]提出了J函数的经验公式，认为J函数与饱和度存在相关关系。以这一理论为基础，很多测井工作者从毛管力出发，通过不同的方法解释含油饱和度，在不同油田都取得一定效果，同时也发现一些问题，总体来看，目前对于毛管力计算含油饱和度的前提条件在认识上还不统一。林茂杰等[2-6]认为可以用毛管力建立高度与饱和度的关系，进而确定油藏的平均含有饱和度；陈赓等[7-13]认为可以从毛管压力得到J函数与饱和度的关系，建立自由水面以上饱和度剖面；吕鸣岗等[14]应用Purcell方法，首先确定储层有效储层孔隙半径下限，再由平均毛管压力曲线获得地层原始平均含油饱和度；肖亮等[15-19]认为，进汞饱和度与渗透率有一定相关性，通过渗透率虚构毛管压力曲线，进而计算含油饱和度；梁忠奎等[11]认为毛管力可以用来计算低阻油藏饱和度；梁小磊[20]在低孔渗油藏用毛管力计算含油饱和度；章成广等[21-23]认为压汞过程中的润湿性问题还有待研究，这对饱和度的计算精度产生很大影响；林会喜等[24-26]认为，除了汞的润湿性问题外，力学平衡也还有待研究。目前测定毛管压力的方法主要有半渗透隔板法、压汞法、离心机法3种方法，半渗透隔板法测试时间长、测定压力范围小，离心法测试速度快，但是，测试压力低、设备昂贵，而压汞法测试速度快，压力范围大，是目前比较常用的一种方法。

1 J函数计算饱和度方法介绍

高度和毛管压力的关系为：

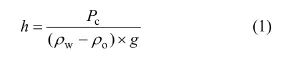
式中：h为自由水面以上的高度，m；ρw为水的密度，g/cm3；Pc为毛管压力；ρo为油的密度，g/cm3；g为重力加速度，g=9.81 m/s2。

毛管压力与饱和度具有一定相关性：

在试验岩石样本数量一定情况下，根据经验公式：

对所有样品用J函数进行平均化，将所有进汞压力点转化为J函数，对全部样本点的J和Sw进行回归，可以得到：

由式(1)，(3)和(4)可得：

式中：C为回归系数；k为渗透率；φ为孔隙度；σ为油水界面张力，N/m；θ为润湿接触角，(°)；Sw为含水饱和度。

J函数拟合示意图如图1所示。从图1可以看出，在回归前，同一个含油饱和度对应不同的J函数，说明油藏中各个点的孔渗不一样，有一定的非均质性；而回归后，J函数与饱和度形成唯一对应的关系。由于实际油藏中孔渗分布非常复杂，在垂向上孔隙半径分布不可能均匀分布，只能通过孔渗等效的方法，通过岩心样品的平均效应来代表实际油藏的平均孔渗。从以上分析可以得出，在J函数计算饱和度方法中需要注意：

(1)按式(3)进行J函数转化时，需使用每块样品的孔隙度、渗透率；

(2)式(4)所应用的样品要足够多，要能充分代表油藏的孔隙特征；

(3)J函数计算公式由连续砂岩模型推导出来，因此，在实际应用过程中，该公式可以应用于垂向上连通的砂体。

图1 J函数拟合示意图Fig.1 Sketch map of J function creating fit curve

2 存在的问题

在利用J函数计算含油饱和度的过程中，根据饱和度和高度的关系，对油藏建立饱和度剖面，油藏剖面如图2所示。岩心样品1，2和3分别取自油藏中A点、B点、C点，其孔隙度分别为1φ，2φ和3φ，渗透率分别为K1，K2和K3，样品的平均孔隙度和渗透率分别为φ和K。由3个样品的毛管压力曲线，通过J函数饱和度法得Sw=f(h,φ,K)的关系式。若3个样品孔渗变化较大，则回归出来的关系式相关系数过低，会造成3个点的饱和度计算值与实际值差别太大。

J函数计算饱和度法存在以下问题：一方面，式(5)中的孔隙度、渗透率是用油田中尽可能多的样品的平均孔隙度、平均渗透率来代表油藏的平均孔渗结构状况，是平均效应，而在计算饱和度剖面的过程中，变为油藏中每个点的孔、渗；若油藏中某些点的孔渗与平均孔渗差别太大，则会导致饱和度解释结果误差变大；另一方面，整个油藏中砂岩的孔渗差别很大，没有将砂岩分类，造成所有类型砂岩均使用同一个公式进行平均化，J函数关系式相关系数可能较低，从而使计算结果不够准确。

图2 岩心样品在油藏中的位置示意图Fig.2 Position of cores in reservoir sketch map

3 孔隙体积法重建毛管压力曲线

决定毛管压力曲线的根本地质因素是岩石本身的孔喉半径及分布，因此，提出一种的重建毛管压力曲线方法，有效解决平均化过程中出现的问题。

利用工区岩石的孔隙度、渗透率、岩石孔喉半径等参数，对砂岩进行总结分类，对每一类砂岩应用孔渗结构法重建毛管压力曲线，进而计算饱和度。

首先，考虑实验室条件与地下油藏条件的差异，将实验室测得压力转化为油藏条件下的油水界面张力。毛管压力曲线每个压力区间端点计算所对应的孔隙半径为：

在已知样品总体积、孔隙度的情况下，通过查找该压力区间端点的进汞饱和度，计算出该压力区间下孔隙半径区间的进汞体积，这个体积代表了样品中该孔隙半径区间所对应孔隙空间的体积Vij(Vij代表第i个样品的孔隙半径rj所对应的体积，0＜j＜k)，以此类推，可以得到所有样品的每个孔隙半径对应的孔隙体积的绝对值。利用式(7)综合计算所有样品的平均孔隙度：

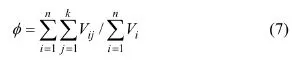
通过查找平均孔隙度所对应的渗透率，可以得到所有样品的平均渗透率。利用式(8)计算出所有样品每个孔隙半径所对应的孔隙空间占总岩石孔隙空间的比例：

结合式(6)，计算出对应的毛管压力，这样，每个孔隙半径对应的体积分数、毛管压力可以虚拟建造1条新的毛管压力曲线，用这条计算的虚拟毛管压力曲线代表整个油藏的平均毛管压力曲线。各等级孔喉体积与虚拟毛管压力曲线示意图如图3所示。这种方法既考虑了孔隙半径，又考虑了不同孔隙半径的分布情况，更加贴近油藏实际情况。

图3 各等级孔喉体积分数与虚拟毛管压力曲线Fig.3 Volume fraction of different pore throat and theoretical capillary curve

4 实例应用

非洲某国东部某区块，正断层发育，储层为古新世河流相沉积的砂岩，主力油层为S层和Y层，S层为曲流河沉积，油层厚度3～15 m，埋深700～1 100 m；Y层为辨状河沉积，油层厚度7～25 m，埋深1 100～1 500 m；部分油层为低阻油层，孔、渗差别大，非均质性强，根据孔隙度、渗透率、孔喉半径等将砂岩分为3类，如表1所示。

由表1可知：Ⅰ类砂岩孔隙度中等，渗透率小，孔喉半径小，整体物性差；Ⅱ类砂岩孔隙度大，渗透率中等，孔喉半径稍大，物性中等；Ⅲ类砂岩孔隙度、渗透率均较大，孔喉半径也较大，物性好。针对3种类型砂岩，利用孔喉结构法重建毛管压力曲线，分别建立3种不同类型砂岩的孔隙结构与虚拟毛管压力曲线，结果见图4～6。

通过虚拟毛管压力曲线，对该区主力油层3种不同类型的砂岩进行J函数转化。Ⅰ～Ⅲ类砂岩J函数回归饱和度图结果如图7～9所示。

从图7～9可见： J函数与含油饱和度有较好的线性关系，相关系数也比较高。Ⅲ类砂岩拟合过程中，曲线成两段式 (图9)，对两端分别进行直线拟合，相关系数也比较高。

根据以上结果，重新整理J函数回归过程，将式(4)变换为：

表1 砂岩分类Table1 Classification of sand

图4 Ⅰ类砂岩孔喉体积分数与虚拟毛管压力曲线Fig.4 Volume fraction of different pore throat and theoretical capillary curve of type Ⅰ sand

图5 Ⅱ类砂岩孔喉体积分数与虚拟毛管压力曲线Fig.5 Volume fraction of different pore throats and theoretical capillary curve of type Ⅱ sand

图6 Ⅲ类砂岩孔喉体积分数与虚拟毛管压力曲线Fig.6 Volume fraction of different pore throats and theoretical capillary curve of type Ⅲ sand

式中：a和b从拟合曲线得到。由式(1)，(3)，(9)可得：

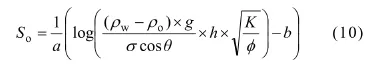
将该方法在研究地区进行应用，对3类砂岩分别建立饱和度-高度关系式，关系式相关系数均在97%以上，可信度较高。含油饱和度结果对比见表2。由表2可看出：Ⅱ类砂岩中，新、旧方法计算的含油饱和度与岩心分析测量值相差不大，在5%以内；在Ⅰ类和Ⅲ类砂岩中，旧方法计算的含油饱和度误差偏大，普遍大于10%，而采用新方法计算的含油饱和度误差在8%以内，明显优于旧方法的结果。

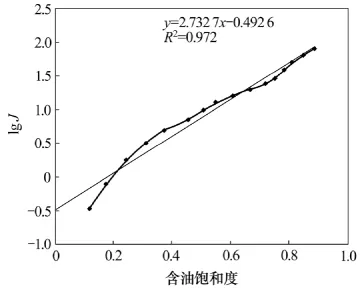
图7 Ⅰ类砂岩J函数回归饱和度图Fig.7 J function creating fit curve with saturation map of type Ⅰ sand

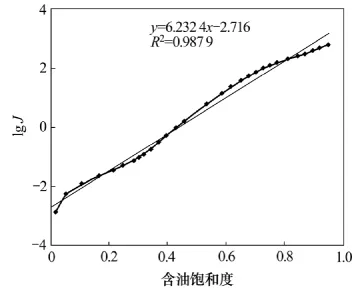
图8 Ⅱ类砂岩回归饱和度图Fig.8 J function creating fit curve with saturation map of type Ⅱ sand

图9 Ⅲ类砂岩回归饱和度图Fig.9 J function creating fit curve with saturation map of type Ⅲ sand

表2 含油饱和度解释结果对比Table2 Comparison of results of oil saturation

5 结论

(1)提出孔渗体积法重建毛管压力曲线，考虑储层中不同类型砂岩孔喉半径及分布情况，形成虚拟毛管压力曲线，为毛管压力曲线平均化提供了一种新思路。

(2)将虚拟毛管压力曲线方法应用于非洲某国东部某区块油藏砂岩，对3种类型油藏砂岩分别建立虚拟毛管压力曲线，J函数取对数后与含油饱和度曲线呈一段式线性相关或二段式线性相关，进行线性拟合后再计算饱和度，其结果精度较高。

[1]Leverett M C.Capillary behaviors in porous solids[J].Transactions of the AIME, 1941, 142: 152-169.

[2]林茂杰, 邹少春.用毛管压力曲线确定孔隙型气藏的原始含气饱和度[J].石油天然气工业, 1993, 13(2): 17-21.LIN Mao-jie, ZOU Shao-chun.Determining initial gas saturation of porosity gas reservoir using capillary pressure curve[J].Natural Gas Industry, 1993, 13(2): 17-21.

[3]张建国, 刘新福.毛管压力法确定含水饱和度及其与老测井解释方法的区别[J].石油勘探开发情报, 2001, 8(4): 61-65.ZHANG Jian-guo, LIU Xin-fu.Water saturation calculation using capillary pressure method and the differences ininterpretation[J].Petroleum Exploration and Development Information, 2001, 8(4): 61-65.

[4]芮捍东.渤海湾盆地东营凹陷原生岩性油藏含油性影响因素分析与定量预测[J].石油实验地质, 2009, 31(3): 221-224.RUI Han-dong.Influential factors analysis and quantitative prediction of oil-bearing characters of the original litholigical reservoirs of Dongying depression, the Bohaiwan Basin[J].Petroleum Geology & Experiment, 2009, 31(3): 221-224.

[5]Archer J S, Wall CG.Petroleum engineering principles and practice[M].Oxford: The Alden Press, 1986: 92-100.

[6]Welge H J, Bruce W A.A restored-state method for determination of oil in place and connate water[J].Production Practice and Technology, 1947: 166-174.

[7]陈康, 赵新军.确定储层含油饱和度的测井-毛管资料综合法[J].江汉石油学院学报, 1995, 17(2): 51-55.CHENG Kang, ZHAO Xin-jun.A method of calculating oil saturation from log and capillary pressure data[J].Journal of Jianghan Petroleum Institute, 1995, 17(2): 51-55.

[8]阎伟林, 田中元, 马陆琴.利用毛管压力资料和测井资料评价H油田碳酸盐岩储层的含油饱和度[J].大庆石油地质与开发, 2008, 27(3): 121-123.YAN Wei-lin, TIAN Zhong-yuan, MANG Lu-qin.Evaluation on oil saturation of carbonate reservoir in H oilfield using capillary pressure and logging data[J].Petroleum Geology & Oilfield Development in Daqing, 2008, 27(3): 121-123.

[9]廖敬, 彭彩珍, 吕文均, 等.毛管压力曲线平均化及J函数处理[J].特种油气藏, 2008, 15(6): 73-75.LIAO Jing, PENG Cai-zhen, LÜ Wen-jun, et al.Average of capillary pressure curve and handling of J function[J].Special Oil and Gas Reservoirs, 2008, 15(6): 73-75.

[10]管耀.利用毛管压力资料求原始含油饱和度方法探讨[J].勘探地球物理进展, 2009, 32(5): 365-369.GUAN Yao.Computing oil saturation using capillary pressure data[J].Progress in Exploration Geophysics, 2009, 32(5):365-369.

[11]梁忠奎, 周灿灿, 杨春梅, 等.利用烃柱高度计算含油饱和度在低阻油层中的应用[J].国外测井技术, 2010, 175: 40-42.LIANG Zhong-kui, ZHOU Can-can, YANG Chun-mei, et al.Using the height of hydrocarbon to calculate oil saturation in low resistance reservoir[J].World Well Logging Technology, 2010,175: 40-42.

[12]梁英, 武富礼, 杜彦军, 等.特低渗岩性油藏原始含油饱和度的确定方法[J].重庆科技学院学报: 自然科学版, 2010, 12(3):4-7.LIANG Ying, WU Fu-li, DU Yan-jun, et al.Calculation of original oil saturation in low permeability lithologic oil reservoir[J].Journal of Chongqing University of Science and Technology: Natural Sciences Edition, 2010, 12(3): 4-7.

[13]王培春, 吕洪志.低阻油层含水饱和度计算方法研究[J].中国海上油气, 2010, 22(4): 104-107.WANG Pei-chun, LÜ Zhi-hong.A research on the method to calculate water saturation for low-resistivity oil pays[J].China Offshore Oil and Gas, 2010, 22(4): 104-107.

[14]吕鸣岗, 毕海滨.用毛管压力曲线确定原始含油饱和度[J].石油勘探与开发, 1996, 23(5): 63-66.LÜ Ming-guang, BI Hai-bin.Initial oil saturation determination by capillary pressure curve[J].Petroleum Exploration and Development, 1996, 23(5): 63-66.

[15]肖亮, 梁晓东, 林雨静.储层原始含油饱和度评价新方法研究[J].石油地质与工程, 2007, 21(6): 53-55.XIAO Liang, LIANG Xiao-dong, LIN Yu-jing.Study on a new method for evaluating initial oil saturation of reservoir[J].Petroleum Geology and Engineering, 2007, 21(6): 53-55.

[16]肖亮, 刘晓鹏, 毛志强.结合NMR和毛管压力资料计算储层渗透率的方法[J].石油学报, 2009, 30(1): 100-103.XIAO Liang, LIU Xiao-peng, MAO Zhi-qiang.A computation method for reservoir permeability by combining NMR log and capillary pressure data[J].Acta Petrolei Sinica, 2009, 30(1):100-103.

[17]刘晓鹏, 肖亮, 张伟.储层毛管压力曲线构造方法及其应用[J].西南石油大学学报: 自然科学版, 2008, 30(6): 126-129.LIU Xiao-peng, XIAO Liang, ZHANG Wei.Constructing method and application of reservoir capillary curve[J].Journal of Southwest Petroleum University: Science & Technology Edition,2008, 30(6): 126-129.

[18]肖忠祥, 肖亮, 张伟.利用毛管压力曲线计算砂岩渗透率的新方法[J].石油物探, 2008, 47(2): 204-207.XIAO Zhong-xiang, XIAO Liang, ZHANG Wei.A new method for calculating sandstone permeability by using capillary pressure curves[J].Geophysical Prospecting for Petroleum, 2008,47(2): 204-207.

[19]童凯军, 单钰铭, 王道串, 等.基于毛管压力曲线的储层渗透率估算模型[J].石油与天然气地质, 2008, 29(6): 812-818.TONG Kai-jun, SHAN Yu-ming, WANG Dao-chuan, et al.Capillary-curve-based model for estimating reservoir permeability[J].Oil & Gas Geology, 2008, 29(6): 812-818.

[20]杨小磊.低孔低渗储层原始含油饱和度解释方法研究[J].国外测井技术, 2010(3): 10-12.YANG Xiao-lei.The study of saturation in low porosity and permeability reservoir[J].World Well Logging Technology,2010(3): 10-12.

[21]章成广, 秦瑞宝.用毛管压力曲线解释原始含水饱和度[J].江汉石油学院学报, 1999, 21(4): 8-10.ZHANG Cheng-guang, QIN Rui-bao.Calculating original water saturation by capillary curves[J].Journal of Jianghan Petroleum Institute, 1999, 21(4): 8-10.

[22]李传亮.用压汞曲线确定油藏原始含油饱和度的方法研究[J].新疆石油地质, 2000, 21(5): 418-419.LI Chuan-liang.On methodology for using mercury injection curves to determine original oil saturation of reservoirs[J].Xinjiang Petroleum Geology, 2000, 21(5): 418-419.

[23]唐衔, 侯加根, 许凡, 等.利用压汞曲线求取油藏原始含油饱和度的研究[J].重庆科技学院学报: 自然科学版, 2008, 10(5):23-26.TANG Xian, HOU Jia-gen, XU Fan, et al.Method of calculating reservoir original oil saturation by mercury injection curve[J].Journal of Chongqing University of Science and Technology:Natural Sciences Edition, 2008, 10(5): 23-26.

[24]林会喜.应用毛管压力资料求取含油饱和度应注意的问题[J].油气地质与采收率, 2003, 10(1): 17-19.LIN Hui-xi.The problems of utilizing capillary pressure data to get original oil saturation[J].Oil & Gas Recovery Technology,2003, 10(1): 17-19.

[25]朱家俊, 耿生辰, 林会喜, 等.也谈压汞资料与含油饱和度的关系[J].大庆石油地质与开发, 2003, 22(5): 32-34.ZHU Jia-jun, GENG Sheng-chen, LIN Hui-xi, et al.Relationship between capillary pressure data of intrusive mercury method and oil saturation[J].Petroleum Geology & Oilfield Development in Daqing, 2003, 22(5): 32-34.

[26]赵国欣, 朱家俊, 关丽.用毛管压力资料求取原始含油饱和度的方法[J].中国石油大学学报: 自然科学版, 2008, 32(4):38-41.ZHAO Guo-xin, ZHU Jia-jun, GUAN Li.Method of applying capillary pressure data to calculate initial oil saturation.Journal of China University of Petroleum: Edition of Natural Science,2008, 32(4): 38-41.