爆破震动频率对边坡稳定性的影响

明锋，祝文化，李东庆

(1.中国科学院 寒区旱区环境与工程研究所 冻土工程国家重点实验室，甘肃 兰州，730000;2.武汉理工大学 土木工程与建筑学院, 湖北 武汉，430070)

爆破振动对边坡稳定性的影响主要体现在两方面：一是导致岩体结构面抗剪强度参数降低；二是使坡体整体下滑力增大，可能导致边坡动力失稳[1]。岩质高边坡在开挖爆破作用下的稳定性分析是个很复杂的问题, 也是一个急待深入研究的领域。目前，对爆破荷载作用下边坡稳定性影响的研究较多。刘佳等[2]分析了地质背景、边坡结构类型、地形地貌、震源位置等因素对边坡稳定性的影响。舒大强等[3]在对高边坡多方案的动力反应计算的基础上，提出了一套计算爆破震动荷载和分析爆破地震对高边坡稳定影响程度的近似方法。谭文辉等[4]探讨了高边坡的动力特性和爆破震动加速度的分布规律。在边坡安全评价指标方面，Ling等[5]用拟静力的方法评价岩体边坡在地震激励及爆破振动作用下的稳定性；刘汉龙等[6]提出用最小平均安全系数作为评价指标；张建海等[7-8]提出用边坡动力安全系数时程中的最小安全系数作为评价指标。陈玲玲等[9]简述了岩质陡高边坡地震动力响应分析的基本原理与计算方法，建立了评价稳定性的计算公式。宋光明等[10]提出了一种基于边坡振动幅频特性的自振频率求算方法，并由实例验证了该方法。秋仁东等[11]研究了坡高、坡角及下覆岩层的弹性模量对岩质边坡自振周期的影响。徐继言等[12]研究了坡高、坡角、弹性模量及泊松比对边坡自振周期的影响, 建立了边坡自振周期的估算公式。在2002年意大利的莫利塞地震中发现，震害较重建筑的自振频率与地震波的卓越频率相近[13]。目前，多采用拟静力法和有限单元法计算边坡稳定安全系数。这两者都没有考虑爆破振动频率、材料的动力性质和阻尼性质等因素的影响[14-16]。由于开挖卸荷，边坡应力场进行了重分布。在爆破荷载的强烈震动作用下，很有可能引发滑坡、崩塌等现象。因此，研究爆破震动对边坡稳定性的影响，对边坡稳定性更具有现实意义。本文作者通过求解边坡自振频率的方法，调整输入荷载的频率，采用动力响应的时程分析方法，研究了在爆破荷载作用下的边坡稳定性。

1 数学模型

1.1 边坡振动的力学模型

岩质边坡受到爆破地震波作用而产生的振动形态十分复杂, 为了简化分析和减少计算量，对边坡及爆破震动进行一些基本假设[10]：

(1)将边坡视为各向同性的均质体。

(2)将爆破震动视为一种简谐震动波。

根据达朗贝尔原理，在爆破震动的短时作用力P(t)的作用下，任意时刻t，边坡体系在地震动时相应的运动方程为：

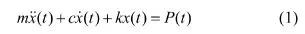
式中：m为岩体单元的质量；c为黏滞阻尼系数；k为岩体单元之间的弹性刚度；P(t)为爆破震动的短时持续作用力。

式中：ζ为阻尼比；γ为频率比；振幅，α为作用力的最大振幅，

边坡在振动过程中存在自由振动和受迫振动。在阻尼作用下，自由振动部分很快消失，只剩下受迫振动部分，从而可以得到其稳态响应：

根据式(3)，在不同的阻尼比下，振幅X同频率比γ的关系曲线如图1所示。从图1可以看出：当γ接近于1时，振幅X迅速增大；当γ大于1时，振幅X迅速减小；在γ=1处达到最大，即产生了共振现象。

图1 频谱特征曲线Fig.1 Amplitude-frequency characteristic curves

1.2 基于时程法的Sarma法

基于时程分析的Sarma法，考虑了爆破过程中条块还受到水平爆破震动惯性力FXi和竖直爆破震动惯性力FYi的作用，将该惯性力引入极限平衡计算[15]。将现场实测振动速度作用于模型，可求得不同位置的加速度。通过条分法确定各条块质量后，根据牛顿第二定律，则可求得条块上作用的水平、竖直向爆破震动惯性力FXi和FYi。为简化计算，施加在各个条块上爆破加速度，均以该条块形心处的加速度为准。求得爆破震动惯性力之后，结合块体极限平衡分析方法中的Sarma法, 即可求得对应于该时刻边坡的稳定性安全系数。

2 工程概况

以南水北调中线段某渠道开挖为例，该渠道为挖方段，挖方深度一般为16.5～27 m，最大挖深为40 m左右。一级～四级边坡系数均为1:0.4，五级坡边坡系数为1:0.7，一级马道以上每增高8 m设一级马道，马道宽2 m。岩性主要为奥陶系灰岩、白云质灰岩；局部地段上覆第四系黄土状壤土和粉质壤土，单层厚度一般为2～4 m。灰岩裂隙较发育，发育规律性差，部分地方已形成溶洞。裂隙面粗糙，多为方解石追踪充填。上部1～3 m灰岩多为强风化，岩体较破碎；下部灰岩为弱～微风化，岩体相对完整。

3 数值模拟

3.1 建立有限元模型

边坡是处于一定地质条件环境中的地质体，影响其振动特性的因素十分复杂[16]。根据前面对计算模型的简化假设，将边坡模型简化为均质岩质边坡。岩体的力学参数见表1，边坡有限元模型图见图2。

表1 岩体的物理力学参数Table1 Physics mechanics parameters of rock

图2 边坡的有限元模型Fig.2 Finite element model of slope

3.2 条块划分

在目前的边坡分析方法中，由于不确定滑面的位置，只能做一些假设，并利用有限元软件，采用二分法进行强度折减，并以塑性区贯通为判断依据，求得滑面的位置(图3)。

根据边坡静力分析求出的边坡的潜在滑移面，对潜在滑体进行条块的划分，滑体共划分为10个垂直条块(图4)。为了避免段位间的叠加，本次选取单段实测爆破的振动曲线。在荷载幅值不变的情况下，改变爆破频率，荷载形式及作用位置见图4。选择条块2，4，6，8，10的形心处作为A，B，C，D，E监测点。

图3 边坡潜在滑移面Fig.3 Potential sliding surface of slope

图4 边坡滑体条块划分Fig.4 Divide land slope into strip

3.3 模态分析

在ANSYS的模态分析中包含了多种模态提取方法，由于边坡的振动特性取决于其低阶频率及振型，因此本文采用子空间法(Subspace)提取了其前4阶固有频率及振型。

从图5可以看出：水平向地震作用时会激发边坡的第2阶振型，垂直向地震作用时会激发边坡的第4阶振型。

表2 边坡固有频率Table2 Natural frequency of slope Hz

图5 前4阶振型图Fig.5 First 4-order vibration shapes of slope

3.4 谐响应分析

在模态分析的基础上，利用ANSYS的谐响应分析模块对边坡进行共振响应分析。在边坡模型上输入最大值为17.5 cm/s速度简谐波进行激振，加载方向垂直于坡面(图4)，加载频率为0～40 Hz，采用完全法对该系统进行计算，位移、应力计算结果分别如图6～9所示。

从图6和7中可以看出：水平向位移主要是在第2阶固有频率处达到最大。越靠近临空面水平向位移越大，而且在边坡坡腰处达到最大。垂直地震作用时会激发边坡的第4阶振型(垂直振动)，在第4阶固有频率处产生共振现象，其他频率的地震波作用时则不会发生共振。

图6 不同测点水平位移频响曲线Fig.6 Frequency response curves of horizontal displacement for different dots of slope

图7 不同测点垂直位移频响曲线Fig.7 Frequency response curves of vertical displacement for different dots of slope

图8 不同测点水平应力频响曲线Fig.8 Frequency response curves of horizontal stress for different dots of slope

从图8和9可知，应力分析结果与位移分析结果相一致。

3.5 瞬态动力学分析

根据谐响应的计算结果，输入频率为14.815 Hz的荷载，其他条件与谱分析一样，采用瞬态动力学分析模块进行计算。选择A，C，E监测点，从位移、速度、及动态安全系数方面分析不同频率爆破荷载作用下边坡的动力响应特征。

图9 不同测点垂直应力频响曲线Fig.9 Frequency response curves of vertical stress for different dots of slope

3.5.1 速度时程曲线分析

不同测点水平和垂直速度时程曲线如图10和11所示。从图10和11可知：速度时程曲线，水平速度普遍要比垂直速度大，这与前面所得到的当固有频率为14.815 Hz时引起水平共振现象的结论相一致。随着距离的增加，水平、垂直速度均在衰减。

3.5.2 位移时程曲线分析

不同测点水平和垂直位移时程曲线如图12和13所示。从图12和13可知：边坡在共振时也存在放大效应，坡顶位移大于坡角位移，坡腰处的位移最大，说明边坡最容易引起破坏的部位在坡腰。水平向位移和竖直向位移均达到最大值。

图10 不同测点水平速度时程曲线Fig.10 Time-history curves of horizontal speed for different dots

图11 不同测点垂直速度时程曲线Fig.11 Time-history curves of vertical speed for different dots

图12 不同测点水平位移时程曲线Fig.12 Time-history curves of horizontal displacement for different dots

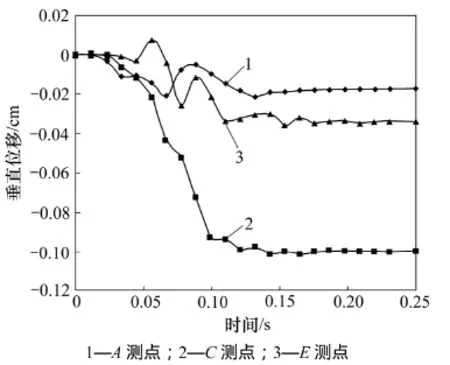
图13 不同测点垂直位移时程曲线Fig.13 Time-history curves of vertical displacement for different dots

3.5.3 动态安全系数时程曲线分析

根据最大单响药量为85 kg时测得的爆破震动曲线，计算了爆破震动主频分别为10.022 Hz，14.815 Hz，21.280 Hz时的3种工况，提取各工况条块形心处的加速度时程曲线。根据Sarma法原理，边坡动力稳性安全系数时程曲线如图14所示。

图14 安全系数时程曲线Fig.14 Time-history curves of safety coefficient

从图14可以看出：随着频率的增加，安全系数的最小值在提高。安全系数在静力安全系数附近振荡，这是由爆破地震波的相变作用引起的。由于爆破作用对安全系数的影响较为短暂，安全系数在经过一段时间振荡后，最终仍与天然状态下的安全系数相接近。

3.6 频率对边坡稳定性的影响

由前面的计算结果可以得到爆破主频与边坡稳定性的关系。爆破频率可由下式计算[17]：

式中：f为频率；Q为最大一段药量；R为爆心距；K，β为场地系数，可通过现场实验确定。

结合南水北调工程某渠道爆破施工，利用实测的爆破震动数据，通过回归得到了K=168.4，β=-0.75，相关系数为0.92。由此得到了特定爆破条件下主频的预测公式：

从式(5)可以看出：在传播介质及传播距离不变的情况下，可以减小装药量来提高爆破主频，这样避免与边坡固有频率接近，提高边坡稳定性安全系数。

4 结论

(1)根据结构动力学理论，利用达朗贝尔原理，构建了爆破地震波作用下均质边坡的数学模型，该模型可用单自由度阻尼系统的简谐振动方程来表示。

(2)通过模态分析，得到边坡的固有频率和振型。结合谐响应分析结果，得到水平向地震作用时会激发边坡的第2阶振型(水平向振动)，垂直向地震作用时会激发边坡的第4阶振型(垂直向振动)，边坡的振动主要发生在坡面处。

(3)通过瞬态分析，得到边坡表面振动速度、位移的分布情况。由于约束的原因，坡腰处的速度、位移最大，坡顶次之，坡脚最小。

(4)根据Sarma法原理，得到了边坡在爆破地震波作用下的安全系数。不同频率的波在边坡产生的峰值加速度不同，因此安全系数的变化幅度有所不同。

(5)随着频率的增加，边坡安全系数提高。在进行爆破施工作业时，可采取适当措施提高爆破地震波的主频，这样可以避免与边坡固有频率接近，达到提高边坡稳定性的目的。

[1]李育枢, 高广运, 李天斌.偏压隧道洞口边坡地震动力反应及稳定性分析[J].地下空间与工程学报, 2006, 2(5): 738-743.LI Yu-shu, GAO Guang-yun, LI Tian-bin.Analysis of earthquake response and stability evaluation for transverse slope at secund tunnel portal[J].Chinese Journal of Underground Space and Engineering, 2006, 2(5): 738-743.

[2]刘佳, 鲁海, 崔颖辉, 等.边坡稳定性的动力影响因素分析[J].北方工业大学学报, 2009, 21(1): 90-94.LIU Jia, LU Hai, CUI Ying-hui, et al.Research on stability of slopes under dynamic forces[J].Journal of North China University of Technology, 2009, 21(1): 90-94.

[3]舒大强, 何蕴龙, 董振华.岩质高边坡开挖爆破震动荷载及其对边坡稳定性影响的研究[J].工程爆破, 1996, 2(4): 39-43.SHU Da-qiang, HE Yun-long, DONG Zhen-hua.Research on vibration load from excavation blasting and its influence on stability of rock high-slope[J].Engineering Blasting, 1996, 2(4):39-43.

[4]谭文辉, 乔兰.爆破震动对公路边坡稳定性影响的数值模拟[J].岩石力学与工程学报, 2005, 24(增1): 4837-4842.TAN Wen-hui, QIAO Lan.Numerical simulation of blasting vibration on highway-slope stability[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(Supp1): 4837-4842.

[5]Ling H I, Cheng A H D.Rock sliding induced by seismic force[J].International Journal of Rock Mechanics and Mining Sciences, 1997, 34(6): 1021-1029.

[6]刘汉龙, 费康, 高玉峰.边坡地震稳定性时程分析方法[J].岩土力学, 2003, 24(4): 553-560.LIU Han-long, FEI Kang, GAO Yu-feng.Time history analysis method of slope seismic stability[J].Rock and Soil Mechanics,2003, 24(4): 553-560.

[7]张建海, 范景伟, 何江达.用刚体弹簧元求解边坡、坝基动力安全系数[J].岩石力学与工程学报, 1999, 18(4): 387-391.ZHANG Jian-ha, FAN Jing-wei, HE Jiang-da.Dynamic safety evaluation of slopes or dam foundation using rigid body-spring element method[J].Chinese Journal of Rock Mechanics and Engineering, 1999, 18(4): 387-391.

[8]薄景山, 徐国栋, 景立平.土边坡地震反应及其动力稳定性分析[J].地震工程与工程振动, 2001, 21(2): 117-120.BO Jing-shan, XU Guo-dong, JING Li-ping.Seismic response and dynamic stability analysis of soil slopes[J].Earthquake Engineering and Engineering Vibration, 2001, 21(2): 116-120.

[9]陈玲玲, 陈敏中, 钱胜国.岩质陡高边坡地震动力稳定分析[J].长江科学院院报, 2004, 21(1): 33-35.CHEN Ling-ling, CHEN Min-zhong, QIAN Sheng-guo.Stability analysis of high-steep rocky slope under earthquake loads[J].Journal of Yangtze River Scientific Research Institute, 2004,21(1): 33-35.

[10]宋光明, 史秀志, 张劲松, 等.利用爆破振动观测求解边坡自振频率[J].金属矿山, 2001(3): 4-6.SONG Guang-ming, SHI Xiu-zhi, ZHANG Jin-song, et al.Working out the natural frequency of slope on the basis of blast vibration monitoring[J].Metal Mine, 2001(3): 4-6.

[11]秋仁东, 石玉成, 付长华.高边坡在水平动荷载作用下的动力响应规律研究[J].世界地震工程, 2007, 23(2): 131-138.QIU Ren-dong, SHI Yu-cheng, FU Chang-hua.General laws of dynamic responses of the high slope under horizontal dynamic input[J].World Earthquake Engineering, 2007, 23(2): 131-138.

[12]徐继言, 刘红帅, 高山.均质岩石边坡自振周期及其估算方法研究[J].世界地震工程, 2009, 25(1): 64-69.XU Ji-yan, LIU Hong-shuai, GAO Shan.Study on natural period of homogeneous rock slope and its estimation method[J].World Earthquake Engineering, 2009, 25(1): 64-69.

[13]Mucciarelli M, Masi A, Gallipoli M R, et al.Analysis of RC building dynamic response and soil-building resonance based on data recorded during a damaging earthquake[J].Bulletin of the Seismological Society of America, 2004, 94(5): 1943-1953.

[14]刘红帅, 薄景山, 耿冬青, 等.岩质滑坡稳定性有限元分析[J].岩土力学, 2004, 25(11): 1786-1790.LIU Hong-shuai, BO Jing-shan, GENG Dong-qing, et al.Rock landslide stability analysis by finite element method[J].Rock and Soil Mechanics, 2004, 25 (11): 1786-1790.

[15]许红涛, 卢文波, 周创兵, 等.基于时程分析的岩质高边坡开挖爆破动力稳定性计算方法[J].岩石力学与工程学报, 2006,25(11): 2213-2219.XU Hong-tao, LU Wen-bo, ZHOU Chuang-bing, et al.Time history analysis method for evaluating dynamic stability of high rock slope under excavation blasting[J].Chinese Journal of Rock Mechanics and Engineering, 2006, 25(11): 2213-2219.

[16]祁生文, 伍法权, 刘春玲, 等.地震边坡稳定性的工程地质分析[J].岩石力学与工程学报, 2004, 23(16): 2792-2797.QI Sheng-wen, WU Fa-quan, LIU Chun-ling, et a1.Engineering geology analysis on stability of slope under earthquake[J].Chinese Journal of Rock Mechanics and Engineering, 2004,23(16): 2792-2797.

[17]张立国, 龚敏, 于亚伦.爆破振动频率预测及其回归分析[J].辽宁工程技术大学学报, 2005, 24(2): 187-189.ZHANG Li-guo, GONG Min, YU Ya-lun.Forecast and regression analysis of blasting vibration frequency[J].Journal of Liaoning Technical University, 2005, 24(2): 187-189.