基于晶界离散分布的多晶硅薄膜晶体管直流模型*

严炳辉 李斌† 姚若河 吴为敬

(1．华南理工大学电子与信息学院，广东广州510640;2．华南理工大学材料科学与工程学院，广东广州510640)

多晶硅薄膜晶体管(TFT)在大规模有源矩阵显示器、大容量存储器等领域得到了广泛的应用［1－2］．业界需要既能准确反映多晶硅TFT物理特性，又便于电路仿真的TFT电流解析模型．因此，多晶硅TFT模型研究已引起广泛的关注［3－6］．

多晶硅TFT沟道中存在着晶粒与晶界势垒，增加了TFT伏安特性的复杂性及模型建模的困难．目前有两类多晶硅TFT 的解析模型［3－8］:(1)基于阈值电压的分区模型［3－5］，该类模型可反映在栅电压的控制下晶界势垒对TFT的伏安特性的影响，但必须引用光滑函数连接各个分区，增加了模型参数和模型的复杂程度;(2)基于表面势的模型［6－8］，该类模型可通过单一的电流方程表示各个工作区，简化了模型参数，但必须假定晶界陷阱均匀分布于整个沟道中，并忽略晶界势垒对载流子输运的影响，偏离了多晶硅TFT的物理特性，给器件仿真带来误差［9］．此外，漏压会改变晶界势垒分布，从而影响沟道有效迁移率，而上述两类模型均忽略这一特点．

有鉴于此，文中根据基于表面势模型的建模思想，将多晶硅TFT沟道按晶粒个数分成若干个小TFT，以解决晶界势垒不利于沟道表面势求解的问题，并结合各小TFT电流相等的原理，建立多晶硅TFT的直流电流模型．该模型考虑了晶界势垒离散分布对TFT伏安特性的影响，可用单一解析方程来描述多晶硅TFT的亚阈值区、线性区和饱和区的漏电流．最后通过仿真验证模型的有效性．

1 模型建模

考虑晶界势垒的沟道表面势求解模型如图1所示．该模型假设其各晶粒大小相等，各晶粒间界与沟道垂直;晶粒串联排列在TFT沟道中，每个晶粒间界和两旁的半个晶粒组成的结合体为一个小TFT，也就是将晶界置于小TFT的沟道中间，将晶粒正中间作为其左边小TFT的漏端和右边小TFT的源端，如图1所示．根据上述模型，求出多晶硅TFT源、漏两端的表面势，结合沟道电流连续性原理来确定各小TFT源端和漏端的表面势函数，进而求出各晶界势垒高度和各个小TFT的沟道迁移率，最后求得多晶硅TFT的漏电流方程和沟道有效迁移率的表达式．

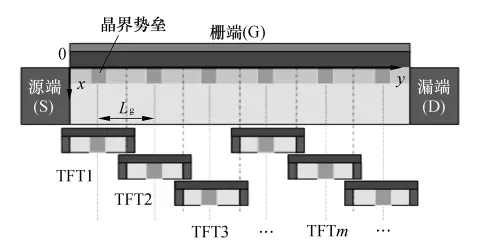
图1 多晶硅TFT分成若干小TFT的示意图Fig．1 Schematic diagram of small TFTs within poly－Si TFT

1．1 小TFT表面势ψs及自由电荷浓度Ui

对于本征多晶硅TFT，施加栅压Vgs后，沟道中晶粒内部产生感生电荷，同时表面势也发生变化，其一维泊松方程为

式中:ψ为沟道表面势;x为氧化层与晶粒中间的界面处，沿沟道深度方向的空间位置;Lg为晶粒大小;εSi为硅材料的介电常数;n为自由载流子密度(体密度)为硅的本征载流子浓度，V为沟道电势，φt为热电压，φt=kT/q，k为玻尔兹曼常数，T为温度，q为电子电量;NT为晶粒中间恰好出现自由载流子时，俘获电荷的晶界陷阱浓度．随着栅压继续增大，俘获电荷的晶界陷阱继续增加，但不影响晶粒中间处的表面势，仅影响晶界势垒高度．

利用高斯定理可得栅电压与表面势的关系表达式:

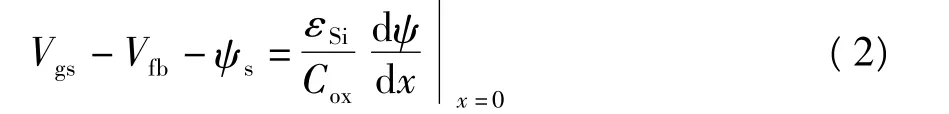
式中，表面势ψs为ψ在x=0处的值，Vfb为平带电压，Cox为单位面积上的栅电容．

沟道中表面势发生变化，同时产生感生电荷．根据电荷守恒定律，沟道感生电荷QC由自由电荷QI与被陷阱俘获的电荷QT组成，即

由式(2)－(4)得到QI与表面势的关系:

结合式(3)和(6)可求得漏、源两端的自由电荷浓度(面密度)，但沟道内各个小TFT的自由电荷浓度(面密度)及表面势还需结合沟道电流方程求得．

为了方便计算，假设沟道各位置的迁移率相等，并忽略晶界势垒对沟道表面势的影响，则TFT沟道的电流方程为

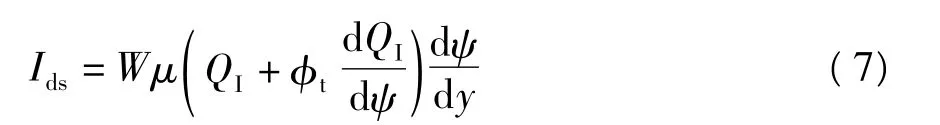
式中，W为TFT沟道宽度，μ为迁移率，y为从源端到漏端的沟道坐标．

对式(7)求积分，可得漏电流:

式中，L为沟道长度，ψss和ψsd分别为多晶硅TFT源端和漏端的表面势．

由式(5)－(8)得到表面势与y的关系:

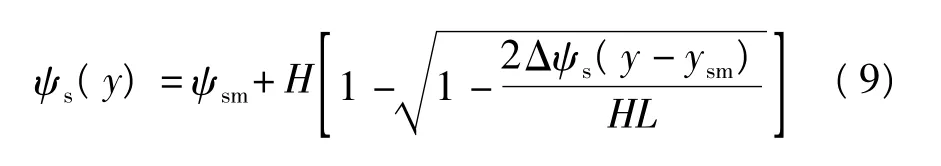
式(9)即是沟道表面势分布函数，结合式(6)可求得沟道自由电荷分布函数．然而，由于晶粒离散分布于沟道，因此，第m个小TFT漏端的电荷浓度和表面势应取y=mLg处的值，源端的电荷浓度和表面势应取y=(m－1)Lg处的值．根据自由电荷与晶界势垒的关系，可求解出第m个小TFT中的晶界势垒高度及迁移率．

1．2 晶界势垒高度与小TFT的迁移率

小TFT中晶界陷阱俘获载流子，使其两旁产生耗尽区，形成晶界势垒［10］．晶界势垒会阻碍晶粒中自由载流子的输运，从而降低小TFT的迁移率．

晶粒内感生电荷的浓度比较低时，所有感生电荷会被晶界陷阱俘获，晶粒完全耗尽;当感生电荷的浓度增加到一定值时，继续增加感生电荷会减小耗尽区，晶粒部分耗尽，此时，晶界势垒达到最大值．此后晶界势垒会随感生电荷增加而降低，因此晶粒部分耗尽时，晶界势垒与自由电荷浓度的关系为［10］

式中，b=8CoxVB0εSit－1ch(qNst)－2，VB0为晶界势垒的最大值，Nst为俘获电荷的晶界陷阱浓度，tch为自由载流子厚度．对于本征多晶硅TFT，当栅极电压较低，即沟道晶粒的费米能级在本征费米能级附近时，晶界势垒可达到最大值．因为晶粒间界存在大量的带尾态，随着费米能级向带隙边缘移动，将有更多的晶界陷阱俘获电荷，所以 Nst远大于 NT．此外，根据Dimitriadis的实验结果［11］，在实际的多晶硅TFT中，晶粒完全耗尽时，晶界势垒高度与最大值相近，其差别对电流的影响可以忽略，因此可用式(10)表示晶粒完全耗尽时的晶界势垒高度．

漏端电压的作用使得自由载流子在沟道各个小TFT中的分布不均匀，导致各晶界势垒高度分布不均匀，如图2所示．

图2 漏压作用下多晶硅TFT中晶界势垒分布图Fig．2 Distribution of grain－boundary barriers in poly－Si TFT under the drain bias

实际上，因为小TFT的沟道长度远小于多晶硅TFT，所以小TFT的源、漏两端载流子浓度相差极小，即 Ui(mLg)≈Ui((m －1)Lg)．结合式(6)和(10)，第m个小TFT的晶界势垒可表示为

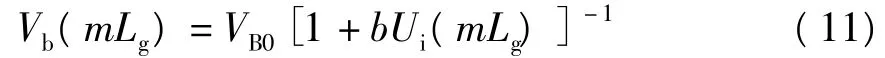
由式(11)可知，从源端到漏端方向上晶界势垒逐渐增高，因此沟道中晶界势垒的平均高度也随之增高，文中定义为漏致晶界势垒不均匀分布效应．此效应是由于漏电压作用下沟道载流子浓度沿漏端方向逐渐降低，使得相应位置的晶界势垒升高而产生．与此相反，在多晶硅TFT沟道横向电场作用下，晶界两旁的耗尽区中，迎着电场方向一边的耗尽区宽度会减小，由此降低晶界势垒高度，即漏致势垒降低(DIGBL)效应［11］．因此考虑 DIGBL效应后晶界势垒的表达式修正为

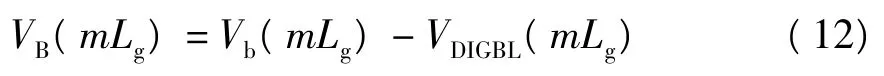
式中，VDIGBL为漏致晶

界势垒降低量［12］，VDIGBL(mLg)=为修正参数，N为自由载流子浓度i(体密度)，Ni(mLg)=CoxUi(mLg)(qtch)－1，E(mLg)为沟道横向电场．

由E=dψ/dy和式(9)，即可求得第m个晶粒处的横向电场:

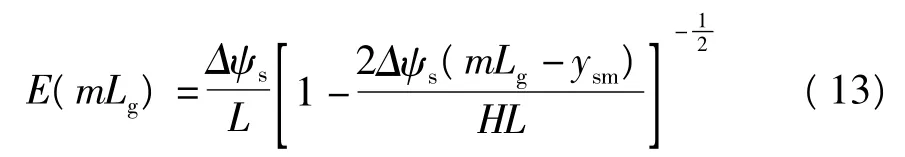
在多晶硅TFT中，晶粒迁移率主要由晶粒间界决定，根据Yang［4］的研究结果可知，沟道中第m个小TFT的迁移率可表示为

式中，μgb为小TFT的迁移率系数．

1．3 多晶硅TFT漏电流

考虑晶界势垒对迁移率的影响后，修正电流方程(7)，得到第m个小TFT的电流方程为

由于流过各个小TFT的电流相等，即

由式(5)、(6)、(14)和(16)可得多晶硅TFT的电流方程为

式中:μeff为多晶硅TFT的有效迁移率，

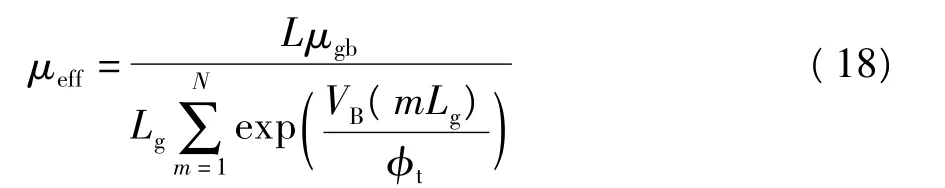
N为多晶硅TFT沟道中小TFT的总数．式(17)和(18)是基于晶粒离散分布的多晶硅TFT直流电流模型．若晶界势垒高度为0，则式(17)可简化为基于表面势的SOI MOSFET电流模型．所以文中模型与通用的MOSFET模型有一致性，便于电路仿真．

2 模型验证和结果分析

为验证文中模型的有效性，将模型的仿真结果与文献［4］的实验数据进行比较．仿真所用的参数值见表1．不同宽长比的多晶硅TFT的输出特性如图3所示．从图3可见，模型仿真结果在较大的栅压范围内与实验数据吻合得较好．由于文中模型没有考虑kink效应［13］，因此在高漏电压时实验数据比仿真结果稍大．在相等的漏电压和栅电压条件下，TFT2的漏电流仿真结果与实验数据之间的偏差比TFT1大．这是由于短沟的TFT2比TFT1具有更强的沟道电场，致使前者的kink效应更明显，其漏电流更大，因此造成上述差别．

表1 仿真中所用的参数Table 1 Parameters used in simulation

图3 两种不同晶体尺寸的多晶硅TFT输出特性的仿真结果与实验数据比较Fig．3 Comparison between simulated results and experimental data of output characteristics for poly－Si TFT with two different transistor sizes

图4 两种不同晶体尺寸的多晶硅TFT的有效迁移率与漏电压的关系Fig．4 Relationship between the effective mobility and the drain voltage for poly－Si TFT with two different transistor sizes

为进一步验证多晶硅TFT的有效迁移率与漏电压的关系．从文献［4］的输出特性数据中提取有效迁移率数据，并将其与文中模型(式(18))的仿真结果进行比较，结果如图4所示，二者具有较好的一致性．由图4可知，当TFT工作在线性区时，沟道有效迁移率受漏电压的影响表现为:漏致晶界势垒的不均匀分布效应明显超过漏致势垒的降低效应，因此有效迁移率随漏电压增加而降低;在较高栅压下，晶界势垒降低，有效迁移率受漏电压影响的程度减弱;相比TFT1，沟道较短的TFT2的有效迁移率受漏电压的影响更小，这是由于沟道较短，导致漏致晶界势垒的不均匀分布效应减弱，同时漏致晶界势垒的降低效应增强，两者共同作用使短沟道TFT的有效迁移率对漏电压的敏感度降低．由此可知，晶界势垒的存在使多晶硅TFT的有效迁移率受制于漏电压，进而影响TFT的伏安特性．当然，在实际的多晶硅TFT沟道中，晶粒大小不一、晶向各异、晶界的位置随机分布．文中为了方便描述多晶硅TFT的电学特性，借鉴现有模型［3－8］的建模方法，假设各晶粒大小相等、各晶界陷阱分布情况相同，因此造成实验数据和模型仿真结果之间的偏差(如图4所示)．然而，文中还讨论了多晶硅TFT的有效迁移率与漏电压的关系，所提模型能较准确地解释有效迁移率随漏电压变化的趋势，模型仿真结果和实验数据之间的误差较小，平均误差在8%以内，在多晶硅TFT模型所容许的范围．

3 结语

文中考虑了多晶硅TFT中晶粒间界的离散分布，采用基于表面势模型的建模方法，建立了多晶硅

TFT的直流电流模型．该模型考虑了漏致晶界势垒的不均匀分布效应和降低效应，用单一的漏电流方程来描述多晶硅TFT的电流特性，能合理解释多晶硅TFT的有效迁移率随漏电压增大而降低的现象．

模型仿真结果与实验数据吻合得较好，从而验证了模型的有效性．

［1］ Meng Z，Wong M．Active－matrix organic light－emitting diode display realized using metal－induced unilaterally crystallized polycrystalline silicon thin－film transistors ［J］．IEEE Transactions on Electron Devices，2002，49(6):991－996．

［2］ Sato A，Momiyama Y，Nara Y，et al．A 0．5μm EEPROM cell using poly－Si TFT technology［J］．IEEE Transactions on Electron Devices，1993，40(11):2126．

［3］ Hatzopoulos A T，Tassis D H，Hastas N A，et al．On－state drain current modeling of large－grain poly－Si TFTs based on carrier transport through latitudinal and longitudinal grain boundaries［J］．IEEE Transactions on Electron Devices，2005，52(8):1727－1733．

［4］ Yang G Y，Hur S H，Han C H．A physical－based analytical turn－on model of polysilicon thin－film transistors for circuit simulation［J］．IEEE Transactions on Electron Devices，1999，46(1):722－728．

［5］ 姚若河，欧秀平．低掺杂多晶硅薄膜晶体管阈值电压的修正模型［J］．华南理工大学学报:自然科学版，2010，38(1):14－17，43．Yao Ruo－he，Ou Xiu－ping．Modified model of threshold voltage for thin－film transistors with low－doped polysilicon［J］．Journal of South China University of Technology:Natural Science Edition，2010，38(1):14－17，43．

［6］ Chen R，Zheng X，Deng W，et al．A physics－based analytical solution to the surface potential of polysilicon thin film transistors using the Lambert W function ［J］．Solid State Electron，2007，51(6):975－981．

［7］ Deng W，Zheng X，Chen R，et al．Subthreshold characteristics of polycrystalline silicon TFTs ［J］．Solid State Electron，2008，52(5):695－703．

［8］ Bindra S，Haldar S，Gupt R S．Modeling of kink effect in polysilicon thin film transistor using charge sheet approach［J］．Solid State Electron，2003，47(4):645－651．

［9］ Wong M，Chow T，Wong C C，et al．A quasi two－dimensional conduction model for polycrystalline silicon thinfilm transistor based on discrete grains［J］．IEEE Transactions on Electron Devices，2008，55(8):2148－2156．

［10］ Serikawa T，Shirai S，Okamoto A，et al．A model of current－voltage characteristics in polycrystalline silicon thinfilm transistors［J］．IEEE Transactions on Electron Devices，1987，34(2):1727－1733．

［11］ Dimitriadis C A，Tassis D H．On the threshold voltage and channel conductance of polycrystalline silicon thinfilm transistors［J］．Journal of Applied Physics，1996，79(8):4431－4437．

［12］ Benzarti W，Plais F，Luca A D，et al．Compact analytical physical－based model of LTPS TFT for active matrix displays addressing circuits simulation and design ［J］．IEEE Transactions on Electron Devices，2004，51(3):345－350．

［13］ 陈婷，李斌．多晶硅薄膜晶体管 kink效应的建模［J］．微电子与计算机，2008，25(6):222－224．Chen Ting，Li Bin．Modeling of kink effect in polysilicon TFT ［J］．Microelectronics and Computer，2008，25(6):222－224．