基于MFD的路网宏观交通状态及影响因素研究*

朱琳 于雷，2 宋国华

(1．北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京100044;2．德克萨斯南方大学，美国德克萨斯州休斯顿77004)

城市道路为网络结构，内部各要素之间直接或间接相连．在机动车不普及的过去，路网内各部分车辆运行畅通，相互之间的关系显得不是很紧密．但随着当前城市机动化的迅速发展，道路系统逐渐趋向饱和，交通运转已经“牵一发而动全身”，区域性的交通问题日益突出．因此，对于交通管理与服务而言，也必须保持全局观，从整个道路网络的大局出发，站在宏观角度解决局部的交通瓶颈问题．对于路网系统而言，传统的对于交叉口、路段的研究和分析方法并不完全适应，而需要基于网络的宏观交通理论与方法．

对于路网宏观交通问题的研究历史并不短暂，Wardrop［1］建立了城市路网的区间平均速度估算模型，模型中考虑了流量、平均道路宽度和绿信比3个因素的影响;Herman等［2-3］将路网中的车辆分为运动车辆和停止车辆两类，并引入二流理论(Two-Fluid Theory)论证了路网中平均行程速度与停车比例系数之间存在指数关系;Godfrey［4］发现了路网平均流量与平均密度之间存在相关性;Daganzo等［5］对此进行了更深入的分析，分析了路网宏观层次上流量、速度和密度等基本交通流参数之间的定量关系，并基于传统交通流基本图模型提出了路网交通流的宏观基本图模型(MFD)的概念．

国内对于路网宏观层面的交通特征及状态研究主要集中在近几年，张和生等［6］提出通过对路段和路口连通性分析研究区域交通状态;姚智胜等［7］、冮龙晖［8］、邹亮等［9］则采用数据融合技术对路网交通检测器数据进行交通参数获取及路网状态判别;王殿海等［10］提出运用二流理论推导路网宏观交通参数之间的函数关系，建立路网宏观交通状态判别模型，并利用最小二乘法标定获取模型关键参数．

从上述国内外研究中可以发现，现有对于路网宏观交通特征研究主要目的在于获取路网交通运行的外在特征，而对于宏观状态形成及变化的影响因素缺乏深入的分析，这对于有针对性的制定区域交通管理和控制措施缺乏足够的支持．加之国内对于路网宏观交通流问题缺乏系统性的分析和应用研究，因此，文中提出以路网交通管理和控制的需求为基本出发点，利用交通流宏观基本图模型为基础研究城市路网的宏观交通问题．

围绕区域路网的“宏观交通状态”，依次从以下几个方面开展相关研究:在介绍交通流MFD模型及其矢量构建方法基础上，挑选以北京西三环为中心的区域路网为对象，构建MFD并实现交通流特征参数的标定;利用不同年份、不同日期的交通流数据，基于MFD中流量－密度散点分布，研究路网宏观交通状态的时间差异;基于MFD所呈现的交通流“磁滞现象”，研究分析影响路网宏观交通状态的根本原因;最后，分析路网结构、交通需求、出行路径等因素对路网宏观交通状态的影响．

1 宏观基本图模型及矢量求解

传统交通流模型是采用统计方法分析历史数据而建立起来的参数关系模型，包括流量－速度模型、流量－密度模型以及速度－密度模型，由于采用关系图的形式直观描述问题，因此，也被称为交通流基本图模型，通常被用于描述单个断面或路段的交通流行为特征．Daganzo等［5］提出了 MFD的概念，从路网整体结构出发，分析道路多个断面或区域路网多条道路的空间平均交通流变量之间的关系．在过去三、四十年中，对于宏观交通流模型的研究主要建立在结构简单、交通畅通的真实路网中或者虚拟的路径选择方式以及静态交通需求条件下，而缺乏针对复杂的城市路网交通流宏观特性的深入研究［11-13］．近几年，大量实测数据分析和仿真研究确定了均衡及非均衡动态交通环境下的宏观交通流变量之间的关系［14-15］，但对于国内复杂的城市及区域路网交通流MFD模型结构及特征等尚未进行分析，更缺乏基于MFD的路网宏观交通运行状态的研究．

最基础的路网宏观交通流参数是全部车辆的平均速度、平均流量和平均密度，因此，基础MFD模型也是描述三者之间的关系．文中基于Edie对于路网三参数的定义［16］，在MFD中采用流量、速度、密度并通过简单算数平均进行求解，即:

式中，qu、ku、vu分别为路网平均流量、密度、速度值，N为分析的检测断面或路段数．

在二维坐标系中表示参数之间的关系，以流量－密度关系为例，如图1所示，基本图曲线上的任一点坐标为(ki，qi)，从原点到坐标点连线的斜率就是速度．对于式(1)，可采用矢量平均算法．假设均匀路网，所有断面流量－密度服从相同的关系图，首先计算两个断面的平均流量、平均密度，根据断面交通流状态(即断面车流密度与临界密度kc的大小关系)不同，矢量平均有3种情况，如图2所示．对于路网内多个断面的平均流量－平均密度关系模型，可采用相同的矢量求解方法．

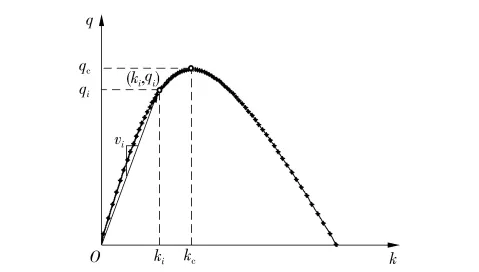
图1 流量－密度关系模型的矢量表达形式Fig．1 Vector expression of flow-density relationship model

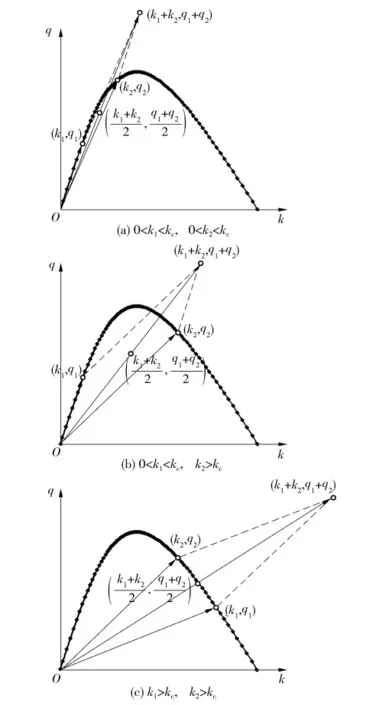
图2 流量－密度关系模型的矢量算法Fig．2 Vector algorithm of flow-density relationship model

采用矢量算法求得路网交通流参数关系散点图后，基于Van Aerde模型［17］可标定交通流宏观基本图的特征参数，即:路网平均自由流速度FS、临界速度(通行能力下的速度)SC、通行能力CAP和阻塞密度JD．

2 路网宏观交通状态实测分析

以北京市西三环及周边区域路网为研究对象(如图3所示)，以实测的微波检测交通流数据为基础，利用MFD矢量算法得到路网平均流量－平均密度关系基本图，分析路网宏观交通状态的时变特征．

图3 北京西三环区域路网图Fig．3 Western 3rd ring-road area network in Beijing

2．1 路网交通流MFD模型

筛选2006年3天和2007年10个周二的RTMS数据，建立两个年份的西三环路网平均流量－平均密度关系散点图，并基于Van Aerde模型［16］标定交通流特征参数，得到路网交通流宏观基本图模型，如图4所示．2007年路网宏观交通流的自由流速度、临界速度和通行能力均有下降，而阻塞密度升高，但4个参数的变化幅度均很小，这说明2007年西三环路网的宏观性能有轻微下降．考虑数据样本量和误差，两个年份的路网宏观交通状态基本一致．

学校可以开展针对任务型教学法的观课、评课比赛。通过学习其他教师的教学优势，提高自身素质，定期检查教案，评比教案。教师需要反复收集材料，处理材料，设定任务，精算时间。这是一个班级成功的关键。备课是一项艰苦的心理活动，教师必须在有限的时间内计划好所有的步骤，准备应对紧急情况的策略。与没有任何准备的纯教学相比，它有不同的效果。在任务的设计上，一个课时的任务数量要根据教学内容来设置。它不能太多或太少。Skehan曾说过，“任务型教学的核心是让学生通过学习语言完成任务。”[1]任务设置必须有针对性。通过完成这项任务，学生将掌握一些技能。老师应该掌握这项工作的困难程度。

在图4中，两个年份的大部分路网平均流量－平均密度关系散点分布在高流量区间，结合图2的MFD矢量求解方法，说明大部分时间段西三环路网内同时存在拥堵路段和畅通路段;而图4中高密度区间没有样本点，说明西三环路网内始终有部分路段交通运行畅通，而这部分路段具有潜在服务能力．

2．2 路网宏观交通状态的时间分布差异

分析不同日期的西三环路网平均流量－平均密度散点分布情况．以2006年3月16日(周四)、17日(周五)和18日(周六)连续3天的西三环路网平均流量－平均密度关系散点图为例．图4(a)为3天数据样本集成后的标定结果，表1是对3天的路网宏观交通流特征参数分别标定的结果，图5中用不同形状散点标出了3天路网平均流量－平均密度关系散点的分布情况．

图4 路网平均流量－平均密度关系图Fig．4 Relationship diagram of average flow and average density on the network

表1 3天路网宏观交通流特征参数标定结果Table 1 Statistical results of frequency distribution of traffic densities on links at different times

图5中，非阴影部分的路网平均流量－平均密度(即低流量、低密度)的关系散点分布集中，而阴影部分散点较分散，且当路网平均密度越接近通行能力下的密度kc时，对应的平均流量值跨度越大，且不同天的分布值域不同．图5显示3天的kc均接近40veh/km/lane，当路网平均密度为kc时，16日对应的路网平均流量跨度最大，为［1160，1540］;17日对应值域次之，为［1220，1465］;18日对应值域最小，为［1340，1500］．散点分布越分散，说明不同时间间隔的路网宏观交通状态越不稳定．

图5 不同天的路网平均流量－平均密度关系图Fig．5 Relationship diagram of average flow and average density on the network of different days

将一天24h划分为5个时段，图6为17日和18日5个时段的平均流量－平均密度关系散点分布情况．

图中显示:(1)同一天不同时段的流量－密度散点分布位置不同，而同一时段的散点较集中．如图6(a)中17日0:00－7:00、20:00－24:00之间的散点主要分布在低密度、低流量区域;7:00－10:00，路网平均密度更多高于kc、平均流量略低于通行能力;10:00－17:00间的平均流量分布区间最高，平均密度在kc两侧;尽管17:00－20:00间部分散点的平均密度也位于kc两侧，但对应的平均流量值较10:00－17:00间的流量值低．图6(b)中，18日不同时段的平均流量－密度关系散点同样分布在不同区间．(2)对比工作日与周末的部分时段，路网平均量－平均密度散点分布区间不同，在上午7:00－10:00间，17日路网平均密度聚集在kc右侧区域，而18日则分布在kc左侧区域．这是因为在工作日，该时段为出行高峰，而周末上午出行时间推迟，高峰尚未到达．

2．3 路网宏观交通状态的磁滞现象

如上文所述，在不同时间段，路网平均流量－平均密度散点在MFD中的分布位置不同，例如:对比17日10:00－17:00和17:00－20:00两个时段，当路网平均密度接近kc时，平均流量却有较大偏差;对比18日7:00－10:00和17:00－20:00两个时段，有相似的情况．

为进一步分析该特征，选取3月17日中午12:00至凌晨0:00间的数据绘制路网平均流量、平均密度时变曲线，以及路网平均流量－密度关系折线图，如图7所示．

图6 不同时段路网平均流量－平均密度关系图Fig．6 Relationship diagram of average flow and average density on the network at different times

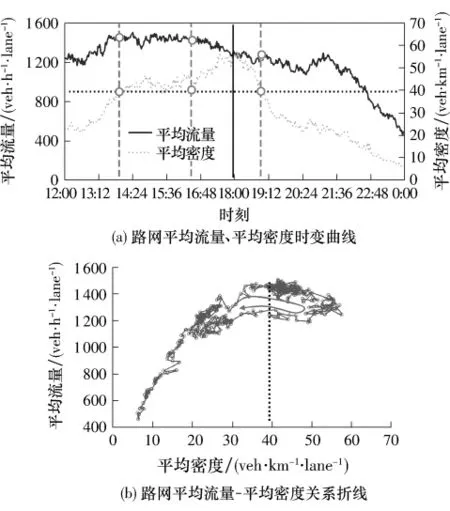
图7 路网平均流量－平均密度时变关系Fig．7 Time-varying relationships of average flow and average density on the network

“磁滞现象”是路网宏观交通状态在时间维度上呈现的另一重要特征，该现象通常出现在路网拥堵发生前后．

3 路网宏观交通状态偏差原因分析

根据MFD矢量求解方法，表征路网宏观交通状态的MFD模型源于单个路段交通流模型．Cassidy等［20］曾采用矢量相加的方法将二维坐标系中的单个断面交通流基本图集成为多个断面的交通流基本图模型，结果表明宏观交通变量散点位置与各断面交通流状态密切相关．Geroliminis等［15］曾指出交通流宏观基本图模型受路网内各路段或检测断面车流密度影响．因此，本节基于实测数据分析各时段路网内路段交通状态差异，探讨宏观交通状态的偏差原因．

根据上文分析，挑选3月17日西三环路网中4个时刻(13:54、16:30、18:54 和20:00)，对比分析路网内56个检测断面车流密度的统计分布情况，如图7(a)所示，13:54、16:30和18:54 3个时间点对应的路网平均密度为40veh/km/lane，20:00对应的路网平均密度为25veh/km/lane．统计结果如图8和表2所示，图8中横坐标表示车流密度分组，根据统计的密度值范围，将断面车流密度按大小划分为20组，以8veh/km/lane为划分区间，最小值为0，最大值为160veh/km/lane．

图8 不同时间检测断面车流密度频数分布Fig．8 Frequency distribution of traffic densities on links at different times

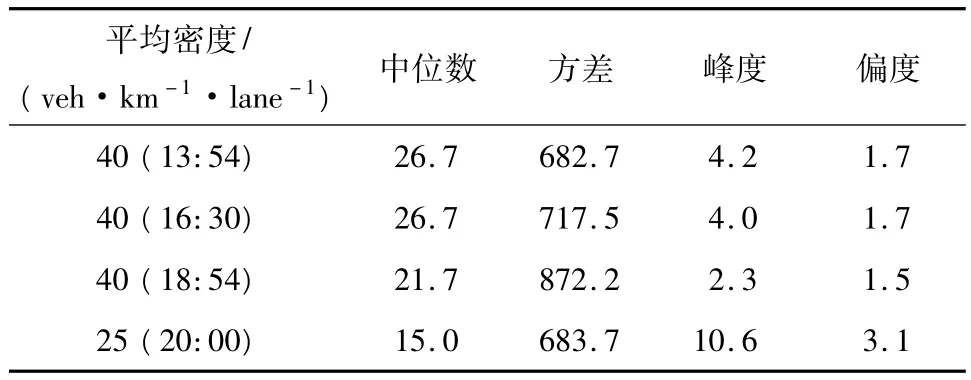
表2 不同时间检测断面车流密度统计分布结果Table 2 Statistical results of frequency distribution of traffic densities on links at different times

从图8和表2中，对比20:00路网车流密度频数分布与其它3个时间点差异更加明显，对应的平均密度、平均流量与其它三组均不同．尽管13:54、16:30和18:54路网平均密度相同，但各检测断面的车流密度频数分布不尽相同，前2个时间分布曲线接近，对应的平均流量值也接近．表2和图8中显示18:54车流密度频数分布峰度偏低，可以看出该时刻高密度的比例较高;偏度与其它两个时刻略有不同，说明分布曲线形状也略有差异．由此可见，路网中各路段车流状态分布是影响路网宏观交通状态的根本原因，而路网内高密度路段的数量和分布是影响路网整体性能的重要因素．

结合图7，18:54路网交通流平均密度处于下降过程，交通状态逐渐好转，但图8和表2结果显示，尽管此时交通需求减少，畅通路段增多，但由于拥堵路段无法迅速消散，拥堵路段比例仍较高，因此，路网平均流量回升速度低于平均密度下降的速度，实际服务的车流量低于高峰之前，即13:54和16:30．由此可见，重点治理拥堵路段问题是防止路网性能下降的重要环节．

4 路网宏观交通状态影响因素仿真分析

研究不同交通条件对路网宏观交通状态的影响是实施路网交通管理与控制的重要依据．因此，基于上文实测数据分析结果，接下来将从交通系统的3个可控要素出发，即路网结构、交通需求以及出行习惯，利用仿真方法说明三要素的变化对路网车流密度时空分布的影响，继而论证三要素对路网宏观交通状态的影响．仍以西三环路网为研究对象，利用仿真模型INTEGRATION构建仿真平台，通过输入不同的要素变量构建不同的交通运行环境．每个方案仿真时长为2h，OD矩阵的输入间隔为15 min，仿真结果的输出间隔为5min，仿真输出结果包括路网每条路段的流量、密度、速度．

4．1 路网结构

通过构建西三环路网及其子路网交通流MFD模型，研究不同区域路网宏观交通状态的差异．

对比两个不同范围的路网:第1个路网是图3中所示西三环区域路网，东西方向距离约3．5km，南北方向距离约12．5km，区域内包含快速路、主干路、次干路和支路等不同等级和功能的路段;第2个路网为西三环子路网，仅包含图3中西三环紫竹桥北至航天桥南约4．5 km的快速路交通走廊及东西方向约1．5km范围内的相交道路．分别向两个路网加载相同背景的交通需求，仿真得到路段流量、密度，集成路网平均流量和平均密度，绘制两个路网的平均流量－平均密度关系如图9所示．

图9显示，两个路网的平均流量－平均密度关系图不同．对于西三环大路网而言，路段数量多，等级差别大，且非干道型的次干路和支路比例较大，不同等级道路上车流状况差异大，集成后的路网平均流量、密度值偏小，得到的路网通行能力、阻塞密度均较低;而子路网范围小且大部分路段为快速路或主干路，路面交通状况差异小，因此路网平均流量及密度均偏高，通行能力、阻塞密度较高．

图9 不同路网平均流量－平均密度关系图Fig．9 Relationship diagrams of average flow and average density on different networks

由此可见，对于不同规模和结构的路网而言，宏观交通状态差别较大，路网结构越均匀，各路段交通状态差异越小，路网整体性能越高．因此，交通管理中应引导交通出行向主干道、次干道、支路等道路均衡发展，协调各等级道路之间的功能，从而提高路网的实际服务能力．

4．2 交通需求

从交通需求总量和时变比例两个角度，分别研究交通需求对路网宏观交通特征的影响．

(1)提高交通需求总量，分析路网宏观交通状态的变化．

分别向西三环路网中加载两组交通需求，第1组为采集的基础交通需求，第2组将基础交通需求总量提高20%，仿真测试并绘制路网车流密度时空分布图以及平均流量－平均密度关系图，如图10所示．

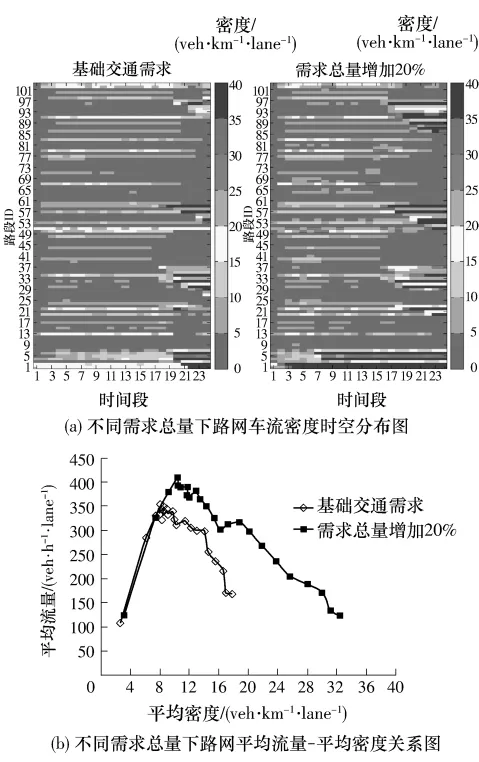
图10 不同需求总量下路网宏观交通状态Fig．10 Macroscopic traffic conditions on the network under different traffic demands

图10(a)为5min间隔输出的西三环主路各路段车流密度．可以看出，交通需求增加后，路网内主要的高密度路段基本一致，但两种方案下相同路段上的密度时间分布不同，部分路段提前进入拥堵．图10(b)显示，交通需求增加后，路网宏观交通状态发生变化，平均流量－平均密度关系曲线的峰值升高，即路网平均通行能力和阻塞密度均提高．对比两种方案的结果:①在仿真初期，平均流量－平均密度关系变化趋势基本一致，此时路网处于畅通状态，路网内交通流分布一致;②增加西三环路网的交通需求，路网通行能力、阻塞密度升高，说明之前由于路网车流分布不均衡导致路网性能下降，实际路网仍有潜在能力;③当路网平均流量达到最大值后迅速下降，密度持续增加，仿真后期，增大交通需求，平均密度升高，但平均流量降低，路网实际服务量下降．

(2)固定交通需求总量，对比均匀时变需求与非均匀时变需求对路网宏观交通状态的影响．

分别向路网内加载均匀时变和非均匀时变的OD矩阵，仿真测试并绘制路网车流密度时空分布图和路网平均流量－平均密度关系图，如图11所示．

图11(a)中显示在均匀需求下路网内车流密度分布均匀，且密度值较低;当交通需求随时间波动时，仿真后40min路网内部分路段车流密度升高，导致路网内滞留车辆逐渐增多、路网平均流量下降(如图11(b)所示)．图11(b)中显示，当均匀加载OD矩阵时，除最初10 min外，其它时段内路网平均流量在通行能力附近波动，平均密度略有升高．

由此可见，交通需求会影响路网宏观交通状态，交通管理者应紧紧抓住这一因素制定相关交通需求控制策略．例如:①尽管交通需求增加提高西三环路网最大通行能力，但却极易引发车流聚集，路网拥堵，总的交通服务量下降．因此，当交通需求达到一定程度时应采取交通限行政策，如尾号限行、车辆限购等．②尽管交通需求时变比例不同，但西三环路网通行能力没发生变化，而需求波动越大，路网越容易发生拥堵，整体性能下降．因此，交通管理者可以据此制定错峰上下班等出行限制和引导措施．

图11 不同时变需求下路网宏观交通状态Fig．11 Macroscopic traffic conditions on the network under different time-varying demands

4．3 路径选择方式

在确定西三环仿真平台中其它输入参数后，选择INTEGRATION模型中的分组反馈选择方式和个体反馈选择方式［21］，分别进行情景仿真．绘制两种路径选择方式下的路网车流密度时空分布图和平均流量－平均密度关系图，如图12所示．

图12(a)显示，当驾驶员路径选择行为调整为个体反馈方式后，路网内部分路段车流很快聚集并迅速蔓延，高密度的路段明显增多，且较分组反馈方式，车流密度分布位置发生变化．对应图12(b)中流量－密度关系曲线，不同路径选择方式影响了路网MFD的形状，改变了路网阻塞密度．选择分组反馈方式，运行中的大部分时间内，路网平均流量在通行能力处波动，之后随着路网密度增大，平均流量迅速下降．选择个体反馈方式，路网平均流量到达通行能力后便处于持续下降趋势，但流量下降速度较慢，路网平均密度也持续升高，且阻塞密度远大于分组反馈方式．

由此可见，驾驶员路径选择方式是影响路网宏观交通状态的另一个重要因素，改变了路网内的交通拥堵时空分布情况，也影响了路网宏观交通状态．据此，交通管理者可结合路网宏观交通状态及变化规律，引导居民调整出行习惯，并通过实施先进的交通信息诱导策略引导驾驶员选择合理的出行路径，从而提高路网整体交通性能和服务水平．

5 结语

以提供交通管理与控制决策支持为最终目标，通过引入交通流宏观基本图(MFD)模型，选取北京西三环区域路网为实例，研究了路网宏观交通状态的时变特征及“磁滞现象”，分析了不同时刻路网宏观交通状态的偏差原因，并探讨了3个交通要素对路网宏观交通状态的影响，结果表明:不同规模和结构的路网通行能力、阻塞密度不同;交通需求总量增加，路网平均通行能力、阻塞密度会增大，但路网更易发生拥堵;交通需求时变波动较大时，路网更易发生拥堵、性能变差;改变车辆路径选择方式没有改变路网评价通行能力，但路网拥堵演变过程改变，阻塞密度不同．文中首次将交通流宏观基本图的理论与方法引入北京市路网宏观交通问题的研究中，并重点从交通管理与控制的角度出发，系统地阐述了不同交通要素对路网宏观交通特征的具体影响，为进一步开展从宏观角度研究城市交通性能及拥堵问题奠定基础．后续还将继续开展路网车流时空分布与宏观交通状态之间关系的定量研究，从而为从微观到宏观层面的交通拥堵治理、交通控制策略制定提供决策支持．

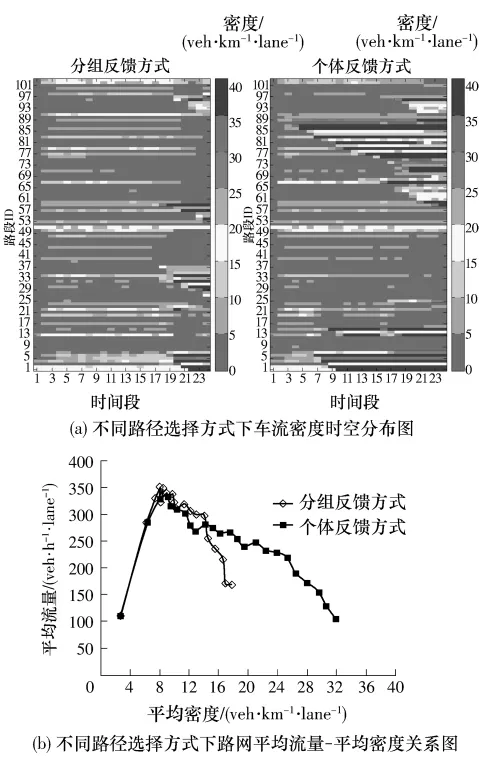
图12 不同路径选择方式下路网宏观交通状态Fig．12 Macroscopic traffic conditions on the network under different routing choice methods

［1］ Wardrop J G．Some theoretical aspects of road traffic research［J］．Proceeding of the Institution of Civil Engineers，1952，1(3):325-362．

［2］ Herman R，Prigogine I．A two-fluid approach to town traffic［J］．Science，1979，204(4389):148-151．

［3］ Herman R，Ardekani S．Characterizing traffic conditions in urban areas ［J］．Transportation Science，1984，18(2):101-140．

［4］ Godfrey J W．The mechanism of a road network［J］．Traffic Engineering and Control，1969，11(7):323-327．

［5］ Geroliminis N，Daganzo C F．Existence of urban-scale macroscopic fundamental diagrams:some experimental findings［J］．Transportation Research Part B:Methodology，2008，42(9):759-770．

［6］ 张和生，张毅，胡东成，等．区域交通状态分析的时空分层模型［J］．清华大学学报:自然科学版，2007，47(1):157-160．

Zhang He-sheng，Zhang Yi，Hu Dong-cheng，et al．Spatialtemporal hierarchical model for area traffic state analysis［J］．Journal of Tsinghua University:Science and Technology，2007，47(1):157-160．

［7］ 姚智胜，邵春福．基于状态空间模型的道路交通状态多点时间序列预测［J］．中国公路学报，2007，20(4):113-117．

Yao Zhi-sheng，Shao Chun-fu．Road traffic multi-sport time series forecasting based on state space model［J］．China Journal of Highway and Transport，2007，20(4):113-117．

［8］ 冮龙晖．城市道路交通状态判别及拥挤扩散范围估计方法研究［D］．长春:吉林大学交通学院，2007．

［9］ 邹亮，徐建闽，朱玲湘．基于融合技术的道路交通状态判别模型［J］．清华大学学报:自然科学版，2007，47(S2):1822-1825．

Zou Liang，Xu Jian-min，Zhu Ling-xiang．Traffic state classification model of travel times based on the fusion technique［J］．Jouranl of Tsinghua University:Science and Technology，2007，47(S2):1822-1825．

［10］ 王殿海，陈松，魏强，等．基于二流理论的路网宏观交通状态判别模型［J］．东南大学学报:自然科学版，2011，41(5):1098-1103．

Wang Dian-hai，Chen Song，Wei Qiang，et al．Discrimination model for macroscopic traffic comditions of urban networks using two-fluid theory［J］．Journal of Southeast U-niversity:Natural Science Edition，2011，41(5):1098-1103．

［11］ Williams J C，Mahmassani H S，Herman R．Urban traffic network flow models［J］．Transportation Research Record:Journal of the Transportation Research Board，1987，1112:78-88．

［12］ Ardekani S，Herman R．Urban network-wide traffic variables and their relations ［J］．Transportation Science，1987，21(1):1-16．

［13］ Olszewski P，Fan H S，Tan Y W．Area-wide traffic speedflow model for the Singapore CBD ［J］．Transportation Research Part A:Policy and Practice，1995，29(4):273-281．

［14］ Gonzales E J ，Chavis C ，Li Y，et al．Multimodal transport in Nairobi，Kenya:insights and recommendations with a macroscopic evidence-based model［C］∥90th Transportation Research Board Annual Meeting CDROM，#11-3045．Washington D C:［s．n．］，2011．

［15］ Geroliminis N，Sun J．Properties of a well-defined macroscopic fundamental diagram for urban traffic［J］．Transportation Research Part B:Methodology，2011，45:605-617．

［16］ Edie L C．Discussion of traffic stream measurements and definitions［C］∥Proceeding of the 2nd International Symposium on the Theory of Traffic Flow．Paris:［s．n．］，1963:139-154．

［17］ Rakha H．Validation of van aerde’s simplified steadystate car-following and traffic stream model［J］．Transportation Letters:The International Journal of Transportation Research，2009，1(3):227-244．

［18］ Gayah V V，Daganzo C F．Clockwise hysteresis loops in the macroscopic fundamental diagram:an effect of network instability［J］．Transportation Research Part B:Methodology，2011，45(4):643-655．

［19］ Geroliminis N，Sun J．Hysteresis phenomena of a macroscopic fundamental diagram in freeway networks［J］．Transportation Research Part A:Policy and Practice．2011，45(9):966-979．

［20］ Cassidy M J，Jang K，Daganzo C F．Macroscopic fundamental diagram for freeway networks:theory and observation［C］∥90th Transportation Research Board Annual Meeting CD-ROM，#11-0657．Washington D C:［s．n．］，2011．

［21］ Van A M．INTEGRATION release 2．30 for windows-user’s guide，volume Ⅰ ＆ volume Ⅱ:advanced model features［R］．Blacksburg U S:Michel Van Aerde＆ Associates，Ltd．，2010．