露天转地下最佳开采模式
王新民,赵建文,张钦礼,吴鹏
(中南大学 资源与安全工程学院,湖南 长沙,410083)
露天转地下开采是集露天和地下2种工艺要素为一体的综合性技术。这种技术可以充分回收矿产资源,提高经济效益,更是一种经济上合理、技术上可行的资源回收方法。目前,露天转地下开采平稳过渡技术内涵及外延尚不完整和明确,为露天采矿和地下采矿的单一集合,仅对露天转地下开采中存在的某些问题进行了探索,如产量衔接、边帮残矿开采、开拓方法等,露天转地下开采关键技术的研究仍处在理论探索阶段[1]。对于露天转地下矿山,必须预先进行露天转地下过渡阶段的开拓系统、采矿方法、安全技术措施的统一规划,兼顾露天、地下安全生产要求,尤其是安全高效的开采模式的确定是实现露天转地下开采平稳过渡的关键。露天转地下最佳开采模式的研究应包括如下内容:采矿方法;保护地表、利于环境恢复;开拓系统布置;产能衔接、安全过渡;地压控制;有效回收资源,损失率、贫化率及保安矿柱的规划等[2]。可见:最佳开采模式的选择是一个涉及多层次、多因素、多目标、多指标的决策过程。对于这样复杂的系统工程,由于地质资料的误差、一些统计方法的局限性、某些价格指标的不确定性、只能定性而不能定量描述的影响因素以及不可预见的各方面因素等,使得最佳开采模式的选择具有极大的模糊性、随机性和未知性。它的推理、判断大多是模糊推理、模糊判断,因而做出的决策也是模糊决策[3]。目前,有些系统工程将模糊数学(Fuzzy)应用于方案的选择中,为在复杂系统设计过程中把那些只能定性描述的模糊概念、模糊推理、模糊判断及模糊决策数学化、定量化提供了理论依据[4-7]。但是,该原理很少应用于开采模式的选择,仅利用模糊数学理论无法确定复杂的指标体系的权重,权重仅通过专家的主观评审选取,带有一定的主观性。层次分析法(AHP)能够通过划分相互联系的各有序层次,把复杂系统问题的各因素、条理化,根据对一定客观现实的判断就每一层次相对重要性给予定量表示,利用数学方法确定表达每一层次的全部元素的相对重要次序的权值[8-9]。本文将层次分析法和模糊数学理论结合起来应用到开采模式选择这个复杂的系统工程中,建立开采模式综合评判模型,用层次分析法客观地确定各因素的权重,再根据模糊数学理论建立模糊综合评判,从而确定露天转地下的最佳开采模式。
1 开采模式综合评判模型构建
在评价对象及因素的选择基础上,根据模糊数学方法构建分层次的指标体系。该指标体系共分为3个层次,分别是目标层U,第一指标层Ui,第二指标层Uij。综合评价(U)的指标体系:一是开拓系统(U1),由于开拓系统已经形成,在评定时只能评价不同的开采模式对现有开拓系统的适应性,即方案灵活适应性(U11);二是采矿方法(U2),可以从采充总成本(U21),采场生产能力(U22),矿石损失率(U23),矿石贫化率(U24),采切比(U25),采空区最大暴露面积(U26),通风条件(U27),实施难易程度(U28);三是边坡稳定性(U3),可以从井下最大涌水量(U31)、炸药单耗(U32)、地质构造(U33)(用地质构造表征岩体结构弱面分析)。
2 层次分析法确定影响因素的权重向量
2.1 构造判断矩阵
在AHP的使用过程中,无论建立的层次结构还是构造判断矩阵,人的主观判断、选择、偏好对结果的影响极大,判断失误可能造成决策失误。AHP的本质是试图使人的判断条理化,但所得到的结果基本依据人的主观判断,当决策者的判断过多的受主观偏好影响,而产生某种对客观规律的歪曲时,AHP的结果不可靠[10]。要使AHP的决策结论尽可能符合客观规律,决策者必须对所面临的问题有比较深入和全面的认识。通过查阅大量文献,并请教相关的专家学者,分析露天转地下开采模式选择的特点构造判断矩阵(表 1)。

表1 判断矩阵U-UiTable 1 Judgment matrix U-Ui
(1) 判断矩阵 U-Ui的元素 wij按行相乘,得到各行元素乘积Mi:

(2) 计算Mi的n次方根:

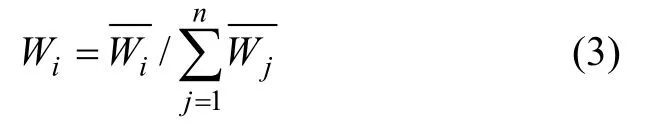
(4) 计算判断矩阵的最大特征根:
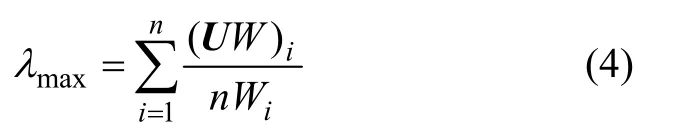
(5) 求判断矩阵的一致性指标CR:

式中,i=1,2,…,n;CI=(λmax-n)/(n-1);RI为平均随机一致性指标。
CR<0.10,说明判断矩阵具有满意的一致性,这样就完成了U-Ui判断矩阵的层次单排序计算。
同理,可得U2-U2j,U3-U3j判断矩阵如表2和3所示。
各二级评价指标的权重系数如下:
(1) U1-U1j:W1=[1],λmax=1,CI1=0,RI1=0,CR1=0;
(2) U2-U2j:W2=[0.314 7,0.314 7,0.130 6,0.130 6,0.083 6,0.047 6,0.030 5,0.019 5]l,λmax2=8.561 5,CI2=0.080 2,RI2=0.080 2,CR2=0.056 9<0.1;

表2 判断矩阵U2-U2jTable 2 Judgment matrix U2-U2j
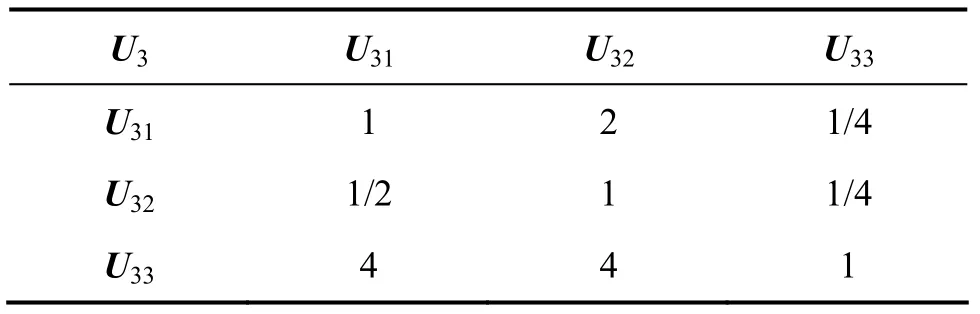
表3 判断矩阵U3-U3jTable 3 Judgment matrix U3-U3j
(3) U3-U3j:W3=[0.208 1,0.131 1,0.660 8]t,λmax3=3.053 6,CI3=0.026 8,RI3=0.52,CR3=0.051 6<0.1。
2.2 层次总排序计算

由CR=0.054 9<0.1可知,层次总排序计算结果(表4)具有满意的一致性。
2.3 隶属矩阵的确定
定量指标的隶属度由隶属函数法确定,非定量指标采用相对二元比较法[11]确定。
针对定量指标所采用的隶属函数法是指对n个方案的m个指标组成的目标特征值矩阵为:
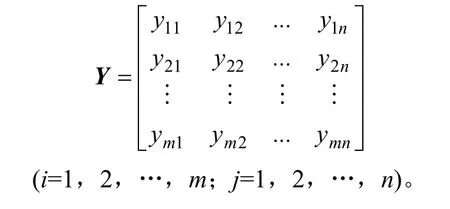

表4 层次总排序权值Table 4 Hierarchy total sorting weights
定量指标可以分为收益性指标与消耗性指标 2类。对于收益性指标,指标越大越好;对于消耗性指标,指标越小越好。则目标相对隶属度公式如下:收益性指标公式 rij=yij/maxyij;消耗性指标公式:rij=minyij/yij。对其进行规格化,得到目标相对隶属度矩阵:
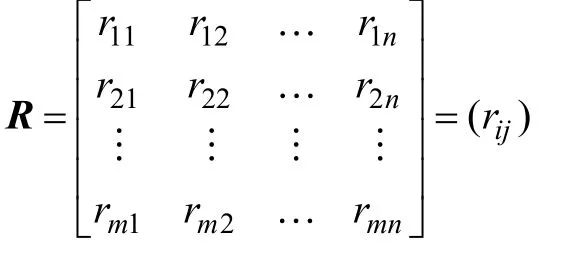
针对非定量指标,采用相对二元比较法。
设系统有待进行重要性比较的目标因素集:X={X1,X2,X3,…,Xm},研究目标集X中的目标就“重要性”进行二元对比的定性排序。目标集中的目标Xk与 Xl作二元对比,即若 Xk比 Xl重要,则令排序标度 ekl=1,elk=0;若 Pk与 Pl同样重要,则令 ekl=0.5,elk=0.5;若 Pl比 Pk重要,则令 ekl=0,elk=1(k,l=1,2,…,m)。由此可得二元比较矩阵E:
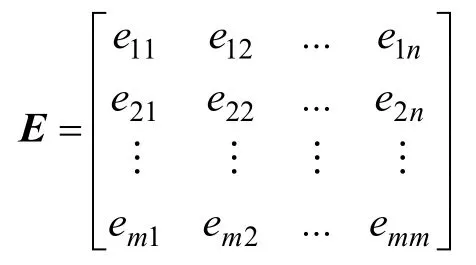
当0≤eij≤1;eij+eji=1;eij=eji=0.5(i=j)时,称矩阵E为关于重要性的有序二元比较矩阵,eij为目标i对j关于重要性作二元比较时,目标i对于j的重要性模糊标度;eji为目标j对于i的重要性模糊标度。将此矩阵按行排序,则(i≠j,i=1,2,…,m)序号表示了目标的相对重要性,根据排序查语气算子与定量标度表[12-13](见表5),可得到非定量指标的隶属度。
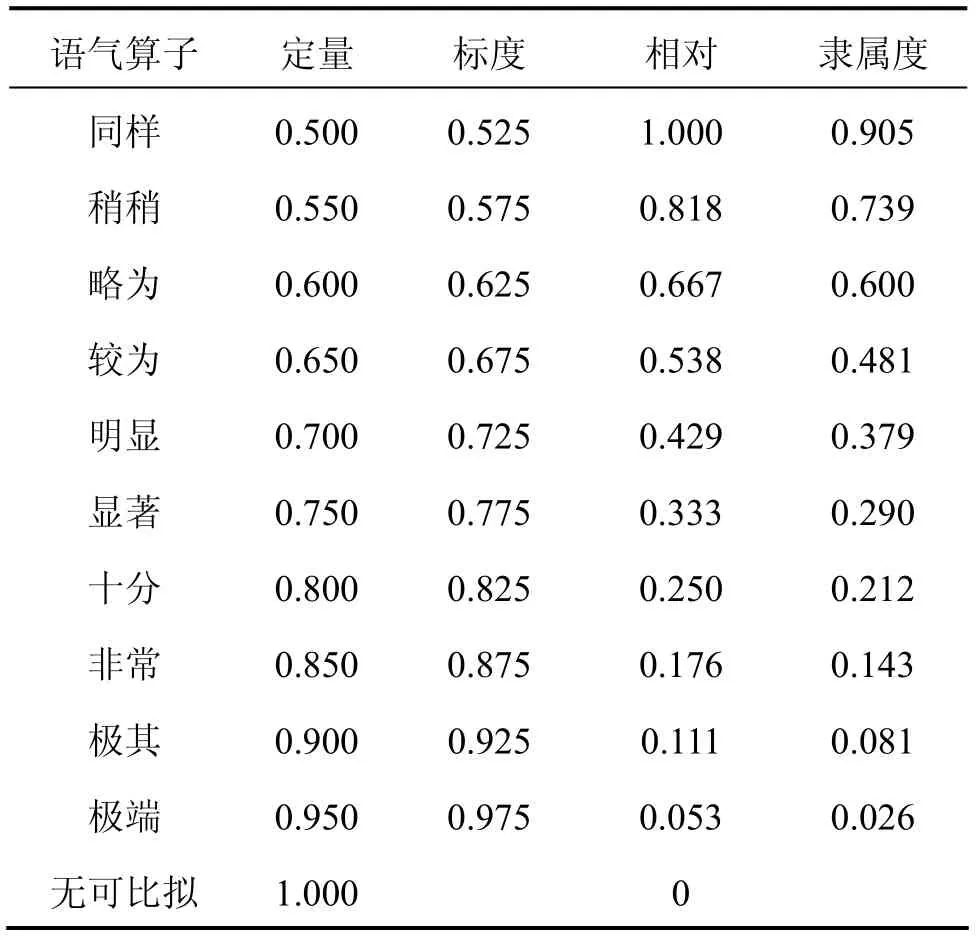
表5 语气算子与定量标度相对隶属度关系表Table 5 Relative membership degree relationship between particle operator and ration mark
3 综合评判
现针对石人沟铁矿露天转地下最佳开采模式的选择,运用上述方法进行综合评判。露天矿转地下开采模式有空场法、充填法及崩落法等,而适合石人沟铁矿的开采模式(以采矿方法分类)有无底柱分段崩落法(简称崩落法开采模式)、分段凿岩阶段出矿法(简称空场法开采模式)、分段凿岩阶段出矿嗣后充填法(简称阶段充填法开采模式)、上向水平分层充填法(简称分层充填法开采模式)等4类开采模式[14-16]。采用建立的露天转地下开采模式综合评判模型对拟选用的4类开采模式进行综合评判,综合评价指标体系见表 6。其中地质构造因素为定性表达的因素,根据评分标准(表7)来确定,规定Ⅰ级评8分,Ⅱ级6分、Ⅲ级4分、Ⅳ级2分;由于不同的采矿方法爆破当量不一样,炸药单耗大的,爆破当量大,因此在评定井下爆破当量时,用炸药单耗来评价。
结合石人沟铁矿情况,根据收益性与消耗性定量指标的隶属函数法,对指标体系中的9个定量指标计算。定量指标的特征向量矩阵:

(1) 根据各采矿方案灵活适应性的特点,得特征向量矩阵:

则隶属度矩阵R25=[0.026 0.875 1 0.875]。
(2) 根据各方案的通风条件,得特征向量矩阵:

则隶属度矩阵R26=[0.0260.290 0.975 0.975]。
(3) 根据各方案的施式难易程度,得特征向量矩阵:

则隶属度矩阵R27=[0.026 0.290 0.975 0.975]。
综合以上可得到综合隶属度矩阵:
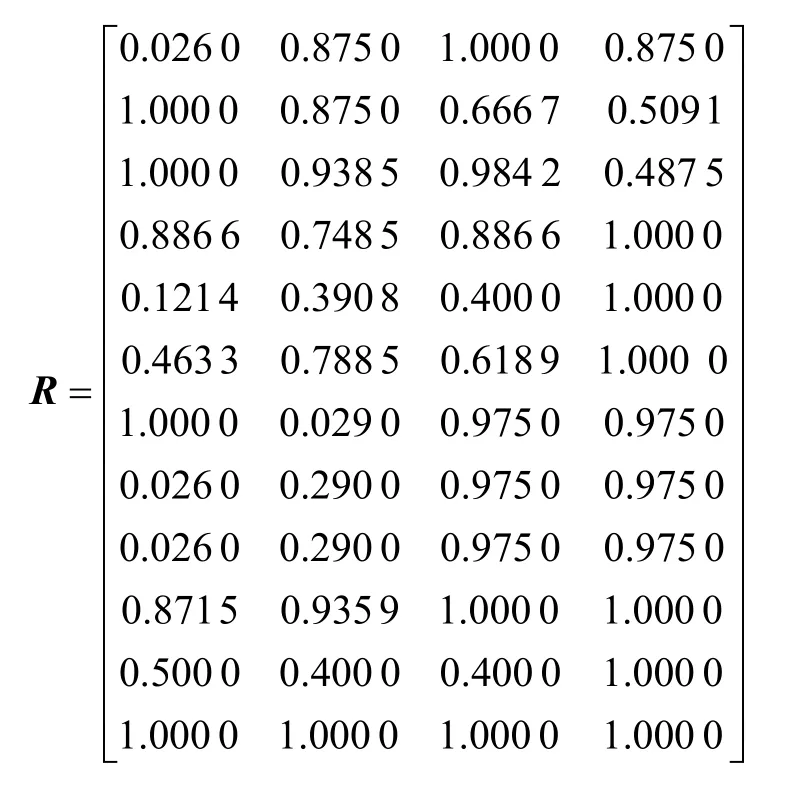
由评价矩阵 R(隶属度矩阵)以及判断矩阵 U,可得方案集A的综合评价为
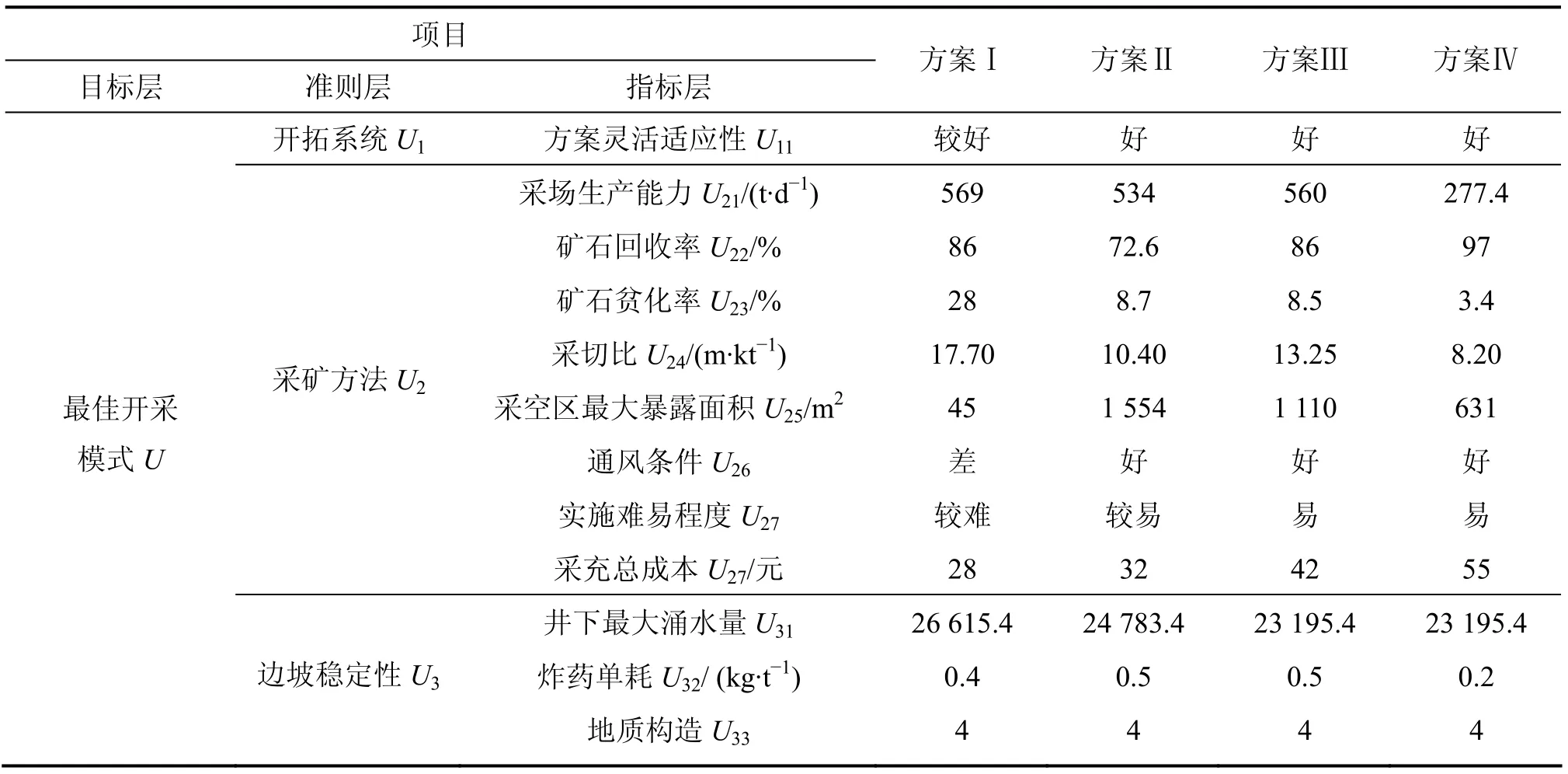
表6 各方案的综合评价指标体系Table 6 Comprehensive evaluation index system of each shame

表7 定性因素评分标准Table 7 Rating criteria of qualitative factors

B=UR=(0.458 2 0.843 2 0.898 8 0.807 5),即各方案的综合优越度为:方案Ⅲ,89.88%;方案Ⅱ,84.32%;方案Ⅳ,80.75%;方案Ⅰ,45.82%。则方案中,崩落法开采模式远劣于空场法及充填法开采模式,其优劣次序为方案Ⅲ,方案Ⅱ,方案Ⅳ,方案Ⅰ,即方案Ⅲ(分段凿岩阶段出矿嗣后充填法开采模式),为最佳开采模式。
通过石人沟矿山的生产实践,验证了本方法的实用性,有效地降低了采矿成本,采场安全、稳定性好,各项技术指标也优于类似矿山,取得了良好的效果,为其他矿山露天转地下开采模式的选择提供了借鉴。
4 结论
(1) 针对金属矿山露天转地下开采这一特定条件,构建了露天转地下开采模式综合评判模型,通过综合分析确定了评判模型的12个评价指标,并利用层次分析法计算指标权重,且通过判断矩阵一致性检验确定合理的权重向量。
(2) 用层次分析法和模糊数学理论建立模糊综合评判模型对石人沟露天转地下开采模式的选择进行分析,得出方案集A的综合评判向量为(0.458 2,0.843 2,0.898 8,0.807 5),从而选用方案Ⅲ,即分段凿岩阶段出矿嗣后充填法开采模式。将研究成果应用于石人沟铁矿,验证了本方法的实用性,为其他矿山露天转地下开采模式的选择提供了借鉴。
(3) 运用层次分析法—模糊数学理论对石人沟铁矿拟选用的开采模式进行了综合评价和模糊综合评判选择,避免了因素过多而难于分配权重的弊端,也避免了单因素决策的片面性和人们主观认识差异所引起的决策失误,特别是在各种影响方案选择的指标出现优越性交叉时,能够做出更为科学、准确、有理论依据的判断。同时,该综合评判模型为矿山露天转地下开采模式的选择提供了新的思路和可靠的技术支撑。
[1]龚清田. 浅析露天转地下开采的几个问题[J]. 有色冶金设计与研究, 2005, 26(4): 1-3.GONG Qing-tian A discussion on some problems in changing open pit mining into underground mining[J]. Nonferrous Metals Engineering & Research, 2005, 26(4): 1-3.
[2]田泽军, 南世卿, 宋爱东. 露天转地下开采前期关键技术措施研究[J]. 金属矿山, 2008(7): 27-30.TIAN Ze-jun, NAN Shi-qing, SONG Ai-dong. Key technical measures in the early period of transition from open-pit to underground mining[J]. Metal Mine, 2008(7): 27-30.
[3]方述成, 汪定伟. 模糊数学与模糊优化[M]. 北京: 科学出版社, 1997: 127-173.FANG Shu-cheng, WANG Ding-wei. Fuzzy mathematics and fuzzy optimization[M]. Beijing: Science Press, 1997: 127-173.
[4]颜春萍. 人机系统价值的模糊综合评价[J]. 湖南科技大学学报: 自然科学版, 2007, 22(1): 78-80.YAN Chun-ping. Fuzzy comprehensive evaluation of human-machine system value[J]. Journal of Hunan University of Science and Technology: Science Edition, 2007, 22(1): 78-80.
[5]周海浪, 曾庆元. 结构振动的模糊可靠性分析[J]. 中南工业大学学报: 自然科学版, 2003, 34(6): 645-647.ZHOU Hai-lang, ZENG Qing-yuan. Fuzzy reliability analysis of structure vibration[J]. Journal of Central South University of Technology: Natural Science, 2003, 34(6): 645-647.
[6]罗一忠, 吴爱祥, 胡国斌, 等. 采场人-机-环境系统可靠性模糊综合评价[J]. 中南大学学报: 自然科学版, 2006, 37(4):804-809.LU Yi-zhong, WU Ai-xiang, HU Guo-bin, et al. Reliability fuzzy comprehensive evaluation of Man-Machine-Environment system in stope[J]. Journal of Central South University: Natural Science,2006, 37(4): 804-809.
[7]鲁光银, 韩旭里, 朱自强, 等. 地质灾害综合评估与区域模型[J]. 中南大学学报: 自然科学版, 2005, 36(5): 877-881.LU Guang-yin, HAN Xu-li, ZHU Zi-qiang, et al. Synthetic evaluation and classification model of geological hazards[J].Journal of Central South University : Natural Science, 2005,36(5): 877-881.
[8]Liu W J, Li Y M. Optimal Adaptive fuzzy control for a class of nonlinear systems[C]//2003 International Conference on Machine Learning and Cybernetics. Xi’an, 2003: 50-53.
[9]Lee H, Tomizuka M. Robust adaptive control using a universal approximation for SISO nonlinear systems[J]. IEEE Trans Fuzzy Systems, 2000, 8(1): 95-106.
[10]李俊芳, 吴小萍. 基于AHP—FUZZY多层次评判的城市轨道交通线网规划方案综合评价[J]. 武汉理工大学学报, 2007,4(2): 205-208.LI Jun-fang, WU Xiao-ping. Synthetic evaluation for urban rail transit line network planning scheme based on AHP—FUZZY method[J]. Wuhan Engineering University, 2007, 4(2): 205-208.
[11]刘增良. 模糊技术与应用选编(2)[M]. 北京: 北京航空航天大学出版社, 1997: 28-46.LIU Zeng-liang. The fuzzy technology and the select material of application (Ⅱ)[M]. Beijing: Beihang University Press, 1997:28-46: 28-46.
[12]Chan P T, Rad A B, Wang J. Indirect adaptive fuzzy sliding mode control, Part Ⅱ: Parameter Project and Supervisory Control[J].Fuzzy Sets and Systems, 2001, 122(1): 31-34.
[13]Xin L L,Geng H, Wang Y M, et al. General limited information diffusion method of small-sample information analysis in insurance[J]. Journal of Shanghai University: English Edition,2007, 11(3): 259-262.
[14]马旭峰, 徐帅, 刘显峰. 眼前山铁矿露天转井下采矿方法研究[J]. 金属矿山, 2008(5): 37-39.MA Xu-feng, XU Shuai, LIU Xian-feng. Research on mining method of Yanqianshan Iron Mine in Transition from open-pit to underground mining[J]. Metal mine, 2008(5): 37-39.
[15]孟桂芳. 露天转地下开采方案的选择和确定[J]. 矿业工程,2009, 7(1): 18-19.MENG Gui-fang. Selection & determining of alternatives to turn open pit mine into underground mine[J]. Mining Engineering,2009, 7(1): 18-19.
[16]毛凤海, 安龙, 李少辉. 铁蛋山矿床露天转地下开采的实践[J]. 金属矿山, 2010(6): 23-25.MAO Feng-hai, AN Long, LI Shao-hui. Practice of transferring from open-pit to underground mining in tiedanshan ore deposits[J]. Metal mine, 2010(6): 23-25.

