基于混沌理论和小波变换的微弱周期信号检测方法

邓宏贵，曹文晖，杨兵初，梅卫平，敖邦乾

(中南大学 物理科学与技术学院，湖南 长沙，410083)

微弱信号不仅意味着信号的幅度很小，而且主要是被噪声淹没的信号，微弱是相对噪声而言的。微弱信号检测是研制出在强噪声下对微弱信号快速、准确、高灵敏度的采集和处理技术，为了检测被噪声覆盖的微弱信号，自20世纪50年代以来，人们进行了长期的研究工作。其处理方法上时域和频率并行发展，分析噪声产生的原因和规律，研究被测信号的特点、相关性以及噪声的统计特性，以寻找出从噪声中检测出有用信号的方法。1992年Mallat提出了奇异性检测理论，提出模极大值重构算法[1]。1995年Coifman等[5]提出了平移不变量小波去噪法。这2种方法对含有若干奇异点的信号去噪效果较好，但是算法复杂，计算速度太慢。随后David等[3-4]提出在二进小波变换基础上的小波阈值去噪概念。此方法计算速度快，适应性广，因此，在许多领域得到了广泛的应用。基于混沌理论的信号处理是近 10年刚发展起来的一门新兴交叉学科，混沌中信号检测和提取具有重要的理论和实践意义。Haykin等[5]利用相空间重构技术和神经网络建模方法研究了在混沌背景下小目标的检测，提出相干检测和非相干检测方法。Huang等[6]利用混沌的窄带特性，使用小波多分辨率分析实现混沌和掩藏在其中的目标信号的分离。Leung等[7]利用混沌具有有限维的特性，提出最小相空间体积法，成功实现了混沌噪声中AR模型参数估计和正弦信号频率估计。此外聂春燕等[8-11]采用混沌理论在微弱信号检测方面进行大量研究。以上这些单用小波分解或混沌系统提取信号的方法都只能在特定条件下取得较好的效果，但是，在强噪声干扰下，混沌相空间结构遭到破坏，这些方法就很难检测出存在的信号。本研究结合小波阈值去噪[12]的能力和混沌系统对噪声的免疫力以及对周期弱信号的敏感性进行信号检测，首先利用小波变换的平滑作用对包含噪声的信号进行简单的有限离散二进小波变换处理，并根据小波分解尺度确定阈值去噪深度，然后把重构的信号作为混沌系统的策动力并入混沌系统，根据梅尔尼科夫判据判断混沌的混沌态，完成信号的检测。

1 小波变换原理

小波变换是1种窗口大小固定但时间窗和频率窗都可以改变的时频局部化分析方法。设ψ (t) ∈ L2(R)(L2(R)表示平方可积的实数空间)，其傅里叶变换为ψ(ω)。当ψ(ω)满足相容性条件时，称ψ(t)为1个基本小波或母小波。将母函数ψ(t)经过伸缩和平移后就可以得到 1个小波序列，所以，对于任意的函数f(t)∈ L2(R )，它的连续小波变换为：

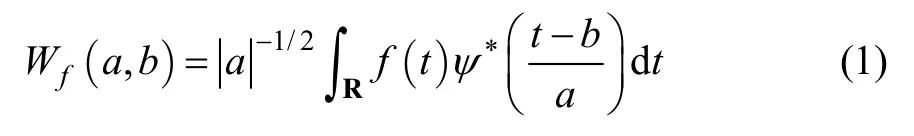
其中：a∈R；b∈R；a≠0；a为伸缩因子；b为平移因子。

其逆变换为

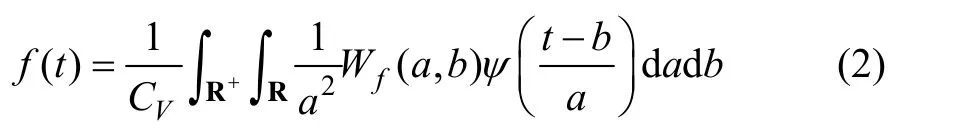
2 检测信息的小波变换去噪

假设从含噪声数据 f(t)复原信号 AS(t)，f(t)=AS(t)+n(t)，n(t)为噪声信号。对信号 f(t)用母小波ψ( t) 的平移和伸缩进行二进离散小波变换。

2.1 小波分解和分解尺度的确定

选择1个小波基对采集到的信号进行分解并确定小波分解层数J。

在实际应用中，一般根据Mallat[13]快速算法实现小波变换，若 fk为信号 f(t)的离散采样数据，则fk=c0,k，f(t)的正交小波变换分解公式为：

其中：k=0, 1, …, N-1。噪声在小波较高分解层上的小波系数较小，可以忽略。而净信号在小波较高分解层中的小波系数较大，即带噪声的信号在小波较高分解层中的小波系数主要是净信号的小波系数。根据这一特性，采用下列方法确定带噪信号的小波分解层数：设当在小波分解第j层中的逼近小波系数和细节小波系数分别为Cj,k和Dj,k。其中，Dj,k的均值为：

方差均值为：

式中：Nj是第j层中细节小波系数Dj,k的个数。则第j层中净信号细节小波系数为：

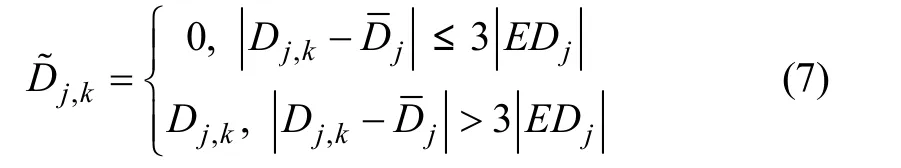
第j层中净信号细节小波系数为：

由ε决定小波分解层，设定1个阈值η (一般η取0.9196较适合)，当ε＜η，说明第j层中噪声的小波系数较大，需要继续进行小波分解。当ε＞η时，说明第j层中噪声的小波系数较小，主要是净信号的小波系数，小波分解截止，得到J。

2.2 作用阈值改进

对小波分解的小波系数选择一个阈值，并对细节系数作阈值处理，即将小波系数绝对值小于等于阈值的全置零，只保留大于阈值的小波系数；由前面第一步分析可知，若阈值δ取得太大，则信号损失太多，若取得太小，则保留有很多细节，去除噪声不干净，影响滤波效果。考虑后面还要把信号导入混沌系统，混沌系统对噪声有很强的免疫能力，适当把在不同分解层上的阈值值取小些，这样可以有效保留微弱的有用信号。由噪声小波变换特性可知：噪声在小波变换后的小波系数均值为0，方差为的白噪声，随着尺度j增加，白噪声小波系数幅值将减小。高斯白噪声是李氏指数(Lipschitz Exponent) α＜0分布。离散的白噪声几乎处处奇异，在小波多尺度分解中，随着尺度的增加，有效信号的小波系数比较清楚，而白噪声的小波逐渐消失。Donoho和Johnstone提出过广义阈值处理：

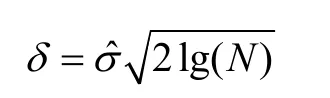
本研究对其进行修正：

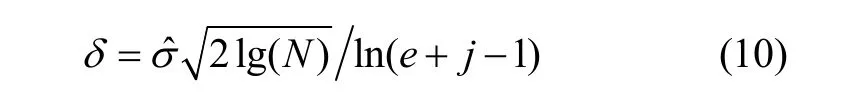
在实际应用中，由于噪声方差σˆ一般是不可知的，去噪处理时可以取可以看到这是一个单调递减函数，随着j的增大，阈值δ逐渐减少。这正好与当尺度增加噪声的幅值减少一致，并且在当j=1时，正好成为Donoho和Johnstone提出的阈值公式。

2.3 对小波变换系数进行硬阈值处理及重构

(1) 根据上一步，对信号进行 J尺度小波分解，得到逼近近似信号CJ和细节信号Dj(j=1, …, J)，保持逼近近似信号CJ不变。

(2) 对J尺度上的DJ，其信噪比比较高，有用信号的能量较大，占有大部分，因此阈值的选取应该更小，以免去除过多有用信号，选取阈值为：

式中：Jσ为信号在J尺度上的方差。

(3) 对细节信号Dj，j=1, 2, …, J-1，信噪比较低，有用信号的能量与噪声的能量比较接近，阈值应在高点，我们用改进的阈值式进行阈值处理，其随着尺度j的变化，与噪声的小波变换各尺度上的传播特性一致。

(4) 重构信号，根据 Mallat快速算法对小波信号进行重建。其重构后信号算法为：

3 小波去噪信号作为策动力导入混沌检测系统

3.1 改进Duffing方程

Holmes型Duffing振子具体形式如下：

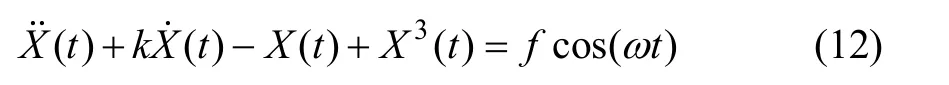
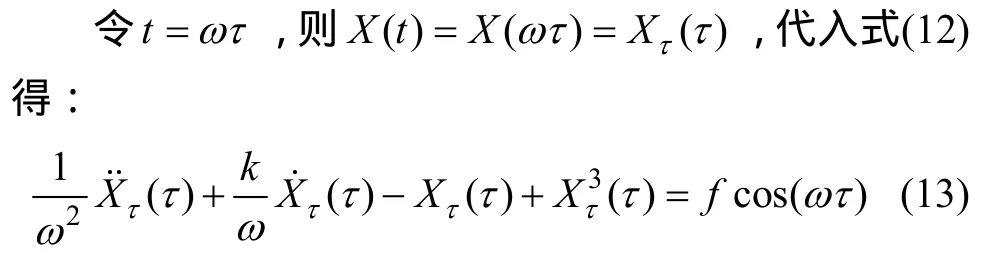
写成状态方程形式为：

3.2 Duffing系统的混沌判据

对于特定系统 Duffing方程来讲，当阻尼比、待测周期信号幅值及策动力频率之间满足一定关系时，混沌系统将进入混沌状态。改进的 Duffing方程的同宿轨道方程的梅尔尼科夫(Melnikov)[14]函数为：

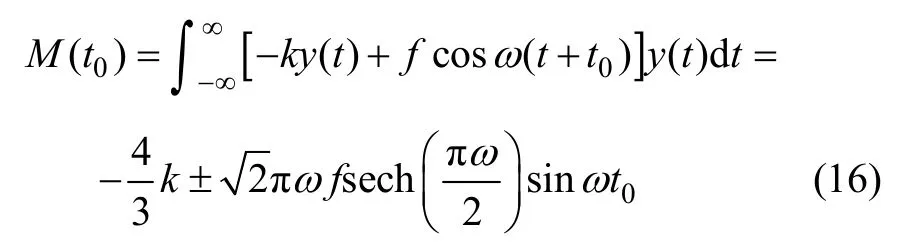
根据梅尔尼科夫判据，系统出现Smale变换意义下的混沌运动的条件是梅尔尼科夫函数存在简单零点，即系统过鞍点(0，0)的鞍点型不动点的稳定不变流形与不稳定不变流形横截相交，系统出现横截同宿点，f/k的最小值称为混沌的阈值，即：

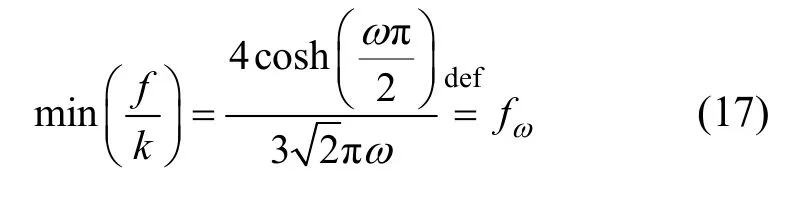
式(17)表明：混沌的阈值与周期策动力频率有关，其关系曲线图如图1所示。当周期策动力频率ω较低时，阈值较低，且变化不大，但随着ω的增加，混沌阈值迅速增大，即在给定的阻尼比k下，f较小的低频段摄动就会使系统发生混沌，而高频段摄动则需要较大的 f，这样可以确定系统进入大周期运动状态的阈值。将判据输入计算机可以判断系统输出状态是处在混沌态还是周期态，避免了直接观察混沌和间歇性运动态分辨不明显的缺陷。

图1 混沌阈值和频率关系图Fig.1 Function of frequency and threshold

3.3 Duffing振子检测重构信号方法

确定频率后，让混沌系统处在混沌临界状态。将经过去噪后频率为的待测周期信号加入系统本身的策动力频率为ω=ω0的Duffing方程时，系统策动力为这时，Duffing方程演化为：

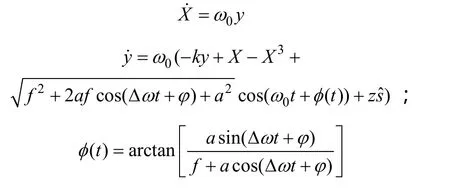
由于加入了周期信号，调节好0ω，其时域图会呈现间歇性混沌现象，实验表明：当待测信号和策动力的频率差Δω=0时，系统始终处于混沌状态或稳定周期运动状态；如图3所示。当0≤Δω≤0.03时，由于Δω很小，F(t)变化比较缓慢，远远慢于相变过程，系统对策动力的缓变能够很好地响应，说明振子相变对小信号很敏感。此时，周期和混沌运动是周期分明出现的，即出现间歇性混沌现象。如图 4所示，其周期为：

当Δω＞0.03时，相变的速度过快，系统较难保证较长时间稳定的混沌或周期运动状态，即较难辨别出有规律的间歇混沌现象，正说明了 Duffing振子的相变对频差较大的周期信号具有较强免疫力，即对频率相同或相差较小的信号敏感。

根据以上分析，本研究利用混沌阵列扫描的方法来实现对强噪声背景下周期弱信号的检测，确定待测信号的频率和幅值。

3.3.1 利用振子阵列测量待测信号的频率

设想使用一有限的阵列，如图2所示，阵列中各振子的固有频率在 1～10之间，使之成为公比为 1.03的等比数列。则振子阵列由78个阵元组成，取ω1=1，ω2=1.03，ω3=(1.03)2，…，ω78=(1.03)77=9.738。这里之所以选择公比为1.03，是考虑到当待测信号和策动力的频率差Δω＞0.03时，很难观测到间歇性混沌现象，故相邻 2阵元 ωk和 ωk+1的振子频率相差不能大于0.03ωk，即 ωk+1-ωk≤0.03ωk，所以，ωk+1/ωk≤1.03，其各振子的固有频率是公比为1.03的等比数列。

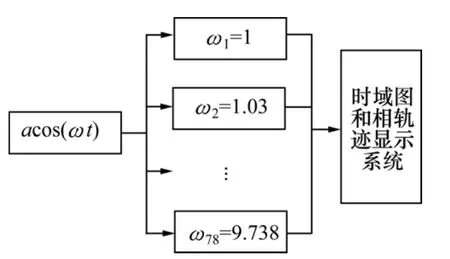
图2 振子阵列实验框图Fig.2 Oscillator arrays experiment diagram

图3 Duffing振子大尺度周期运动图(Δω=0)Fig.3 Great scale periodic movement state of Duffing oscillator (Δω=0)

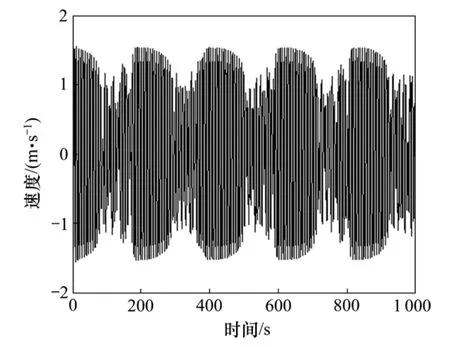
图4 间歇性混沌运动现象Fig.4 Intermittent chaotic motion

如果频率在 1～10之间的信号被输入到阵列中，根据梅尔尼科夫判据确定阈值f′，使系统为混沌临界状态，那么，在且仅在2个相邻的振子上发生稳定的间歇性混沌现象，假如为第k与第k+1个振子，其他振子仍然处于混沌状态，所以，待测信号频率ω必定满足：

根据式(18)，通过测量两振子间歇性混沌的周期就可以精确地确定信号的频率待测信号频率为：

3.3.2 相位锁定测量待测信号的幅值

在频率测定时，间歇性周期段中振幅最大的时刻是系统相位和待测信号相位相同的时刻，通过锁相实现幅值测定。锁相后慢慢减小f至f′′，使系统重新回到混沌状态，此时，信号幅值为a f′ f′′= - 。

4 小波阈值去噪和混沌系统结合的周期微弱信号检测

基于前面的分析以及对小波阈值去噪和混沌系统检测信号算法的改进，本文作者提出如图5所示原理的算法，先用小波函数将待测信号进行自适应多尺度小波变换、灵活的去噪处理和重构信号，再把重构信号后的信号作为混沌振子的策动力并入混沌系统，调节混沌检测频率。通过观察混沌系统的时域图或相空间重构图状态变化，即可以检测出淹没在强噪声中的周期微弱信号。

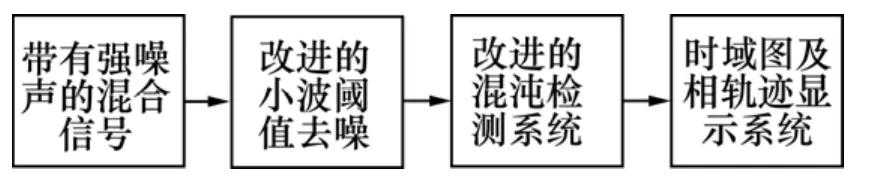
图5 信号检测的基本原理Fig.5 Basic principle diagram of signal test

5 仿真测试和分析

为了验证本研究方法的有效性和优越性，分别对混沌系统、小波-混沌系统[15]和改进的小波-混沌系统用MATLAB7在不同频率下进行仿真测试，并对最低门限和信噪比进行比较分析，用强白噪声和周期微弱信号的混合信号作为待测信号(如图 6所示)。采用本研究提出的算法对信号进行检测，在试验了sym8，db4，haar和coif1等常用几个小波函数后，选用db4作为信号去噪的小波函数，混沌系统采用四阶Runge-Kutta法，取步长h=0.01，k=0.5，初值选为(1，1)，调节频率ω，阈值根据梅尔尼科夫函数确定，使混沌系统处在周期临界状态(如图7所示)。

(1) 加入纯噪声信号：将高斯白噪声zs引入系统，并不断调整噪声方差，发现混沌系统仍处在混沌状态。这说明混沌系统对噪声有一定的免疫能力。

(2) 加入混有噪声的周期信号：固定噪声不变，用3种方法检测频率分别为ω=1下的混合信号，并且逐次递减周期信号的幅值(0.000 01)，反复测试，通过程序判别和观测得到相应的最低门限和信噪比(SNR)，如表1所示。

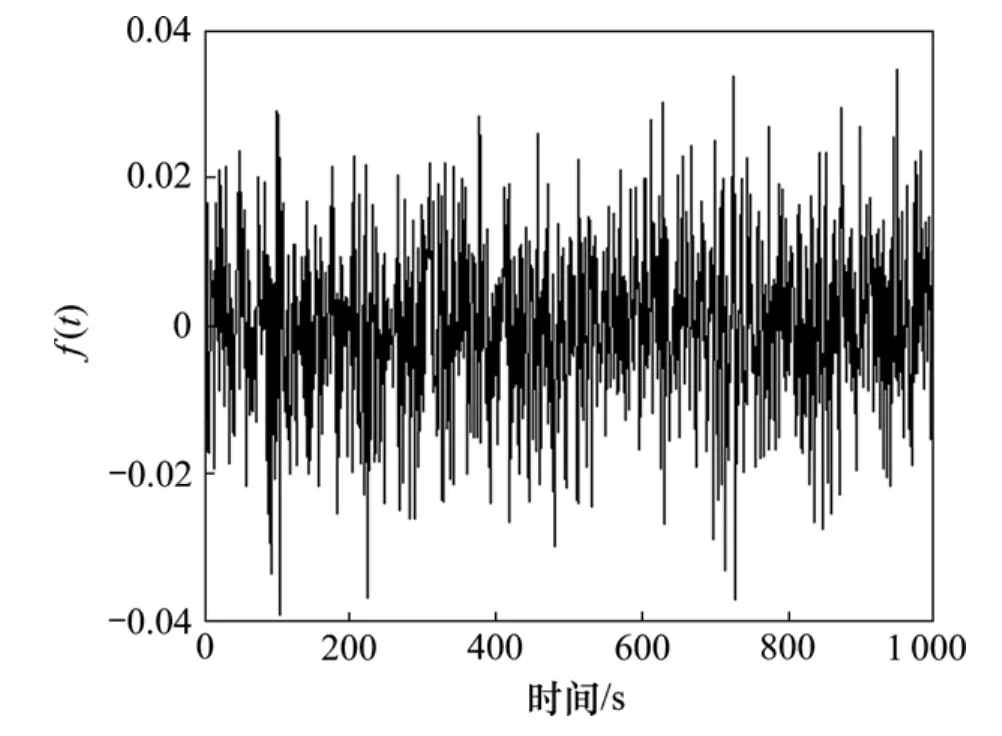
图6 混有强噪声的原始信息Fig.6 Original signal with strong noise

图7 混沌相轨迹的临界状态Fig.7 Phase trajectory of chaotic boundary state

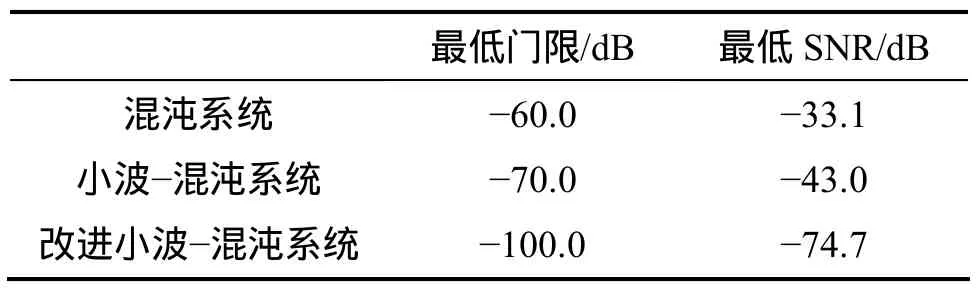
表1 不同检测方法的检测结果比较Table 1 Test results of different methods

(3) 频率和幅值测定：用本研究方法检测f(t)=0.000 245cos(1.02t)+n(t)的周期混合信号，把信号经过小波去噪后，再并入混沌系统。发现相轨迹在ω0=1和ω0=1.03上会转换为大尺度周期运动，时域图呈现间歇混沌现象(如图 8所示)。可得到Δω1=2π/301.75，Δω2=2π/638.41，得ω= 1.020 5 rad/s；同时检测的幅值a f′ f′′= - =0.000 242。

图8 间歇混沌现象时域图Fig.8 Time-domain plots of intermittent chaotic motion

从检测出的信号幅值看，存在一定误差，这误差部分是由于小波阈值去噪处理后信号的减弱，部分是混沌检测的最低门限和最低信噪比而导致的。但是，其检测出的频率误差非常小，在 0.04%以内。从最低检测门限和最低信噪比看，本研究的微弱信号检测方法明显优于混沌系统和小波-混沌系统，证明了本方法可以用于一定环境下的信号检测。

6 结论

(1) 根据小波变换的多分辨率和混沌系统对噪声的免疫功能以及对微弱周期信号的敏感性，通过对小波阈值去噪方法进行改进和采用梅尔尼科夫混沌判据，提出结合小波阈值去噪和混沌 Duffing振子的微弱周期信号检测新方法。

(2) 该检测方法克服了以往小波分解对尺度确定的盲目性和阈值选择的不合理性以及对混沌临界状态与周期态区别的模糊性。

(3) 该方法直观、高效且检测精度高，能有效检测到较强噪声背景下的微弱周期信号。

[1]Mallat S, Hwang W L. Singularity detection and processing with wavelets[J]. IEEE Transactions on Information Theory, 1992,38(2): 617-643.

[2]Coifman R R, Donoho D L. Translation-invariant denoising wavelet and tatistics[M]. New York: Springer-Verlag, 1995:125-150.

[3]David L D. De-noising by soft-thresholding[J]. IEEE Transactions on information theory, 1995, 41(3): 613-627.

[4]LIN Ya-ting, CAI Jian-li. A new threshold function for signal denoising based on wavelet transform[J]. IEEE Computer Society, 2010: 1(3): 200-203.

[5]Haykin S, Li X B. Detection of signal in chaos[J]. Proceeding of IEEE, 1995, 83(1): 94-122.

[6]HUANG Xian-gao, XU Jian-xue. Unmasking chaotic mask by a wavelet multiscale decomposition algorithm[J]. International Journal of Bifurcation and Chaos, 2001, 11(2): 561-569.

[7]Leung H, HUANG Xing-ping. Sinsoidal frequency estimation in chaotic noise[J]. ICASSP, 1995, 2(3): 1344-1347.

[8]聂春燕. 混沌理论及基于特定混沌系统的微弱信号检测方法研究[D]. 长春: 吉林大学通信工程学院, 2006: 1-134.NIE Chun-yan. Research on the weak signal detection method based on the chaos theory and specific chaotic system[D].Changchun: Jilin University. School of Communication Engineering, 2006: 1-134.

[9]李月, 祁放, 张铭, 等. 微弱正弦信号的一种新的混沌检测系统[J]. 仪器仪表学报, 2004, 25(4): 19-20.LI Yue, QI Fang, ZHANG Ming, et al. The detection of weak sine signals using special chaotic system[J]. Chinese Journal of Scientific Instrument, 2004, 25(4): 19-20.

[10]汪金山, 汪晓东, 施晓钟, 等. 基于 Duffing混沌系统微弱信号检测的数值分析[J]. 仪器仪表学报, 2005, 26(8): 33-34.WANG Jin-shan, WANG Xiao-dong, SHI Xiao-zhong, et al.Numerical analysis for weak signal detection based on duffing chaotic system[J]. Chinese Journal of Scientific Instrument, 2005,26(8): 33-34.

[11]张健, 王竹萍, 吕宁, 等. 基于混沌理论的检测技术进展[J].电子器件, 2005, 28(2): 307-311.ZHANG Jian, WANG Zu-ping, LU Ning, et al. Development of detection technology based on chaos theory[J]. Journal of Electron Devices, 2005, 28(2): 307-311.

[12]ZHU Lai-dong, LIAN Xiao-qin, JIANG Yuan-zhi. Application of wavelet transform in signal de-noising and realization with Matlab[J]. Beijing Technology and Business University, 2009,27(2): 46-49.

[13]Mallat S. A theory for multiresolution signal decomposition; the wavelet representation[J]. IEEE Trans Pattern Anal and Machine Intell, 1989, 11(7): 647-693.

[14]刘曾荣. 混沌的微扰判据[M]. 上海: 上海科技教育出版社,1994: 114.LIU Zeng-rong. Perturbation criteria for chaos[M]. Shanghai:Shanghai Science and Technology Education Press, 1994: 114.

[15]张勇, 纪宝宜. 基于混沌振子和小波理论检测微弱信号的研究[J]. 电子测量技术, 2009, 32(6): 40-43.ZHANG Yong, JI Bao-yi. Study of weak signal detection based on chaotic oscillator and wavelet theory[J]. Electronic Measurement Technology, 2009, 32(6): 40-43.