液力缓速器部分充液流场大涡模拟及特性预测

李雪松，程秀生，苗丽颖

(吉林大学 汽车工程学院，吉林 长春，130022)

液力缓速器作为一种辅助制动装置，依靠工作轮内液流的作用将车辆的动能转化为液体的热能，再通过冷却器散热的方式实现车辆制动[1]。当液力缓速器工作在部分充液工况下，其内部是复杂的黏性、不可压缩、非稳态气-液两相流动，流场测试试验较复杂，且设备昂贵。随着计算机技术和计算流体动力学的迅速发展，对液力缓速器内流场进行数值模拟的方法比较经济可行。为全面揭示液力缓速器流场的内部特性以及内外特性之间的变化规律，目前国内学者常用雷诺平均法(RNS)进行流场的数值计算[2-4]，其弊端是忽略了湍流的若干细节，所以，对封闭的雷诺时均方程进行求解并不能有效地模拟流动中分离、涡旋以及扩散等现象[5]。本文作者借助CFD软件平台，采用更为准确的大涡模拟法对液力缓速器部分充液流场进行数值模拟，获取液力缓速器内部流场速度和压力分布特性，以及不同充液率下内流场结构的变化和两相体积分布情况，并基于流场数值解计算液力缓速器的外特性。

1 控制方程及计算模型

大涡模拟(LES)是介于直接数值模拟(DNS)与雷诺平均法(RANS)之间的一种湍流数值模拟方法,是目前CFD研究的热点之一[6-8]，其基本假设是：动量、能量、质量方程及其他标量主要由大涡输运；流动的几何和边界条件决定了大涡的特性，而流动特性主要在大涡中体现；小尺度涡旋受几何合边界条件影响较小，并且各向同性，直接求解大涡，而小尺度涡对大尺度涡运动的影响则通过一定的模型在针对大尺度涡的瞬时N-S方程体现出来[9]。

LES的控制方程是对N-S方程在波数空间或者物理空间进行过滤得到的，通过去掉比过滤宽度或者给定物理宽度小的涡旋，得到其控制方程：

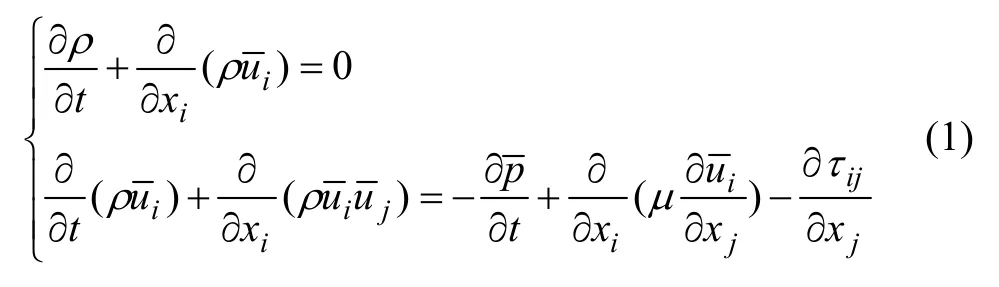
为使控制方程组封闭，必须建立亚格子尺度模型(SGS模型)，目前应用最广泛的漩涡黏性模型方程为：

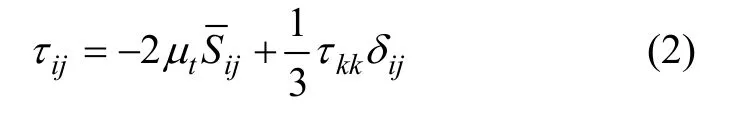
式中：δij是“Kronecker delta”符号(当i=j时，δij=1；当 i≠j时为亚格子尺度的湍动黏度，根据Smagorisnsky-Lily模型定义，其中LS为网格滤波宽度。

式中：k为 VonKarman常数，k＝0.418 7；CS为Samagorin常数，CS=0.1；d为到最近的壁面的距离；V为计算单元体积。

根据液力缓速器样机建立的三维模型以及提取的计算区域网格模型分别如图1和图2所示。定子和转子循环圆有效直径分别为293 mm和296 mm，其叶片数量分别为34和36，均为40°前倾叶片。考虑到液力缓速器定子内有进出油口，定子叶片厚度不同，工作流道几何结构不是周期对称，因此，选取整个流道空间作为计算模型，网格单元总数为794 640个。

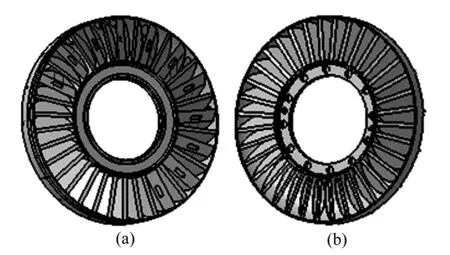
图1 液力缓速器CAD模型Fig.1 Hydraulic retarder CAD model

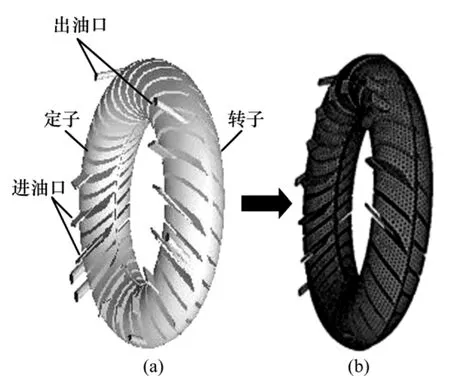
图2 液力缓速器计算网格模型Fig.2 Computational mesh models of hydrodynamic retarder

2 数值计算方法

2.1 控制方程的分离式求解法

流场数值计算的本质就是求解离散后的控制方程组，其基本过程是在空间上将计算域离散成许多小的体积单元，在每个体积单元上对离散后的控制方程组进行求解。求解方法可分为分离式求解法和耦合式求解法。分离式求解法通常用于不可压缩流体数值计算，其求解时同时考虑所有控制单元，顺序、逐个地求解各变量代数方程组。目前工程上使用最广泛的压力修正法，其单个时间步的求解过程如图3所示。本文运用大涡模拟法对液力缓速器内不可压缩的三维瞬态流场进行模拟，也必须采用分离式求解法求解其控制方程组[10-11]。

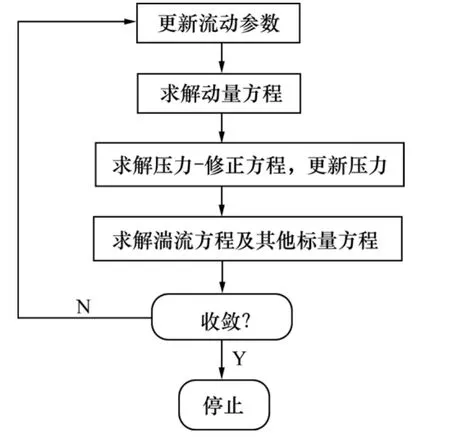
图3 分离求解法计算流程图Fig.3 Flow chart for segregated method

2.2 可动区域耦合计算的滑动网格法

液力缓速器的瞬态特性主要体现在其工作腔内液体的流动状态为湍流非稳态流动，当转子转速一定、工作腔内充液率保持不变时，转子和定子之间相对位置的不断变化引起工作流道内的流场特性呈现周期性的变化，当缓速器工作腔内的充液率及转子转速不断变化时，工作流道内呈现复杂的非稳态流动形态。

为了对转子和定子工作流道进行统一计算，对转子和定子的接合面采用了滑动网格理论来传递两个区域之间的参数。滑动网格法是模拟多移动参考系流场的最精确的瞬态计算方法，其基本原理为：将计算区域中相邻子单元的分界面互相耦合形成“网格分界面”，数值计算中单元区域在离散步骤中沿着网格分界面相互滑动(旋转或平移)，同时分界面也随时间发生变化(如图 4所示)[12]。滑动网格模拟的瞬态问题大部分是时间周期性的，即计算区域的速度是周期复现的。

设T为瞬态计算的周期，在计算区域的一些流动特性函数Φ为

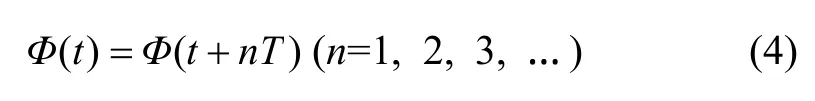
转子在一个周期T内运动2π，又其转速为1 200 r/min，则计算周期T可用下式计算：

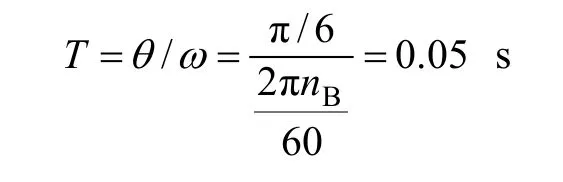
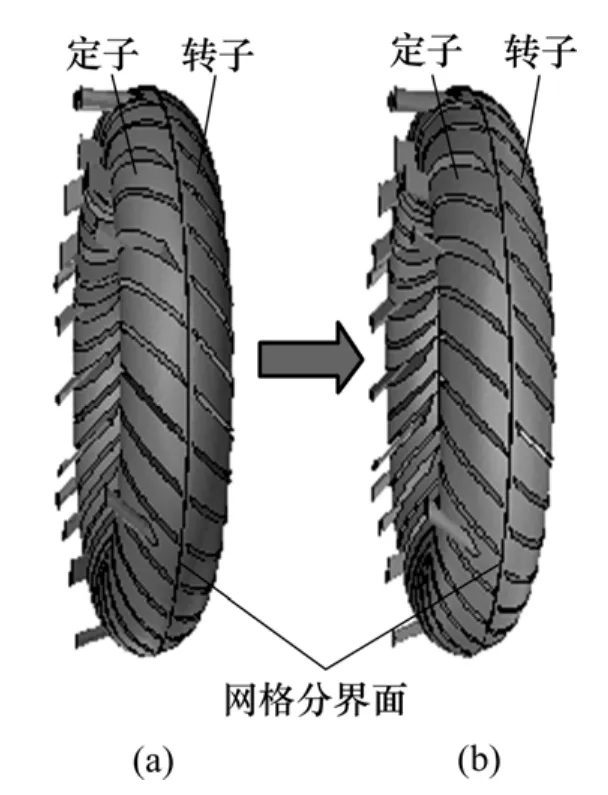
图4 网格滑移前后叶轮之间相对位置Fig.4 Relative position of impellers for sliding mesh theory

单位时间步长以不大于单位网格单元大小为选取原则，文中选取的单位时间步t=0.12 ms。

液力缓速器工作在部分充液状态时，气相与液相之间相互混掺，将混合模型与欧拉模型交替运用在其两相流数值计算中，在多相流模型中首先采用混合模型获得初始解，并以此作为起点，启动欧拉模型继续计算。在制动特性研究中往往关心液力缓速器内外特性的关系，即转子转速、充液率以及制动转矩的变化规律，而这主要是由液相起支配作用，因此设定液相为主相，气相为附加相。

假设液力缓速器内的循环液体作等温流动且没有泄露，认为其在流动过程中为不可压缩黏性流体，且流体与叶轮间的流固耦合作用不致引起流道的变形。流道内壁与叶片表面近壁处速度场计算采用速度无滑移边界条件，进出油口采用压力边界条件。

3 数值计算结果分析

为了准确掌握液力缓速器内部分充液时的流场分布特性，对转子转速为1 200 r/min，充液率f分别为25%和75%的数值计算结果进行对比分析。

3.1 节面流场特性分析

液力缓速器内不同充液率下叶片压力面的静压力分布如图5所示。较高的充液率能导致较大的静压力，因为当转子转速相同时，充液率越大，流体密度也越大，则引起的静压力越大。将不同流动单元中压力面的静压分布(图 5中(Ⅰ)～(Ⅳ))对比分析发现：其分布趋势相同，即从循环圆中心到外环，静压力递增，入口处出现局部高压区，主要是由于定-转子之间过大的转速差导致此处所受液流冲击最大所致；在循环圆中心，涡旋和二次流现象频繁，因此存在环形低压区。充液率较高时，叶片内的压差较大，液力损失也大。

不同充液率下吸力面的静压力分布如图6所示。由于入油口分布在不同流动单元内叶片吸力面上，因此不同流动单元内吸力面静压分布差别较大(图 6中(Ⅰ)～(Ⅳ))。转子叶片中，液流离心力作用使得叶片根部出现高压区；定子吸力面内没有大面积高压区，低压区则是由于冲向压力面的液流在吸力面产生了尾流造成的。由图6中(Ⅲ)和(Ⅳ)可见：定子叶片的进油口附近压力较低，正是为了保证液流以高速进入工作腔。

3.2 弦面流场特性分析

图7所示为不同弦面相对速度矢量分布。中间弦面的涡旋及二次流动现象几乎均布在各流动单元内两叶轮的交接处，这主要是由于压力面和吸力面之间存在较大压差。此外，该弦面内流体质点间的相对剧烈运动也是导致涡旋形成的重要因素，充液率越高，涡旋在各流动单元内分布越均匀[13-14]。如图中A处所示，充液率较低时，在进油口较集中的部分流动单元内出现了逆流以及小涡旋。

图8所示为相对应的弦面静压力分布图。从整体来看，不同充液率时压力分布趋势相同。充液率为75%时，整个弦面内的压力差以及吸力面与压力面之间的压差较25%充液时大。压力差是使液流偏离循环流动方向形成二次流的重要因素[15]，与图7对比可发现逆流及二次流较明显的部分流动单元内，其静压值也偏低。

图5 压力面静压分布Fig.5 Static pressure distribution of pressure surface

图6 吸力面静压分布Fig.6 Static pressure distribution of suction surface

图7 弦面相对速度矢量分布Fig.7 Velocity vector distribution of chord surface

图8 弦面静压分布Fig.8 Static pressure distribution of chord surface

3.3 液相体积分布

图9所示为不同充液率时的液相体积分布。由于液体在工作腔内的循环流动，使液相主要集中在流道外环，而气相分布在内环。充液率为75%时，工作流道的大部分区域被液相占据，而在循环圆中心区域形成气环；充液率为25%时，气相占据了工作区域的大部分空间。

4 性能预测与试验对比

通过对液力缓速器内流场进行瞬态数值计算，可以得到转子叶片表面的速度和压力梯度，据此获得转子叶片表面各单元的压力和剪切力，再通过对旋转轴求矩可得到该单元对旋转轴的作用力矩。对所有转子叶片表面单元进行积分求和即可得到流体作用在转子上的总力矩。滑动网格模拟的瞬态问题与时间t有关，经过若干周期，转矩T已经随时间进行周期性变化，因此可以进行数据采集。

表1和表2所示分别为数值计算结果以及在汽车动态模拟国家实验室液力传动试验台获得的试验数据。由表1，2和图10可知：基于三维瞬态流场数值解的转矩计算结果与试验测试结果吻合较好，最大相对误差在8%以内，说明采用的数值计算方法可以较准确地预测液力缓速器的性能。

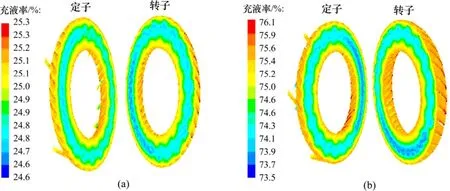
图9 液相体积分布Fig.9 Volume distribution of liquid-phase

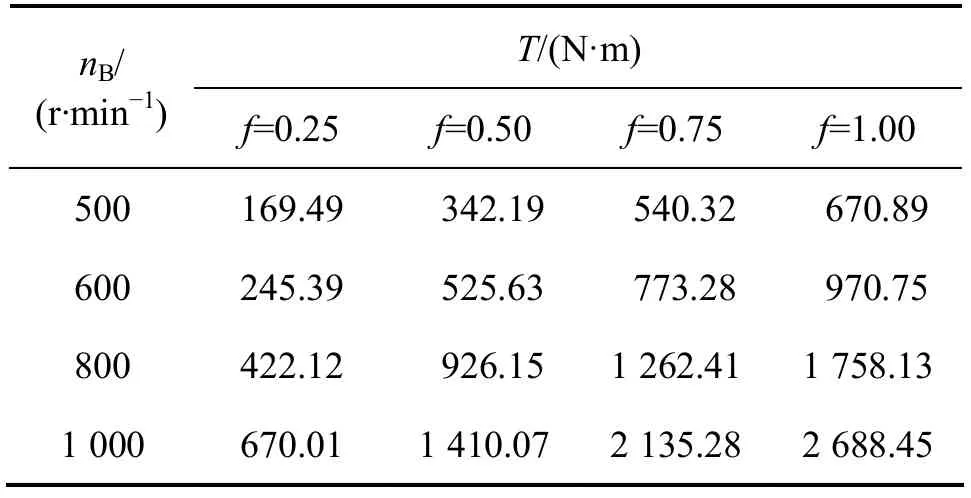
表1 数值计算结果Table 1 Numerical simulation results

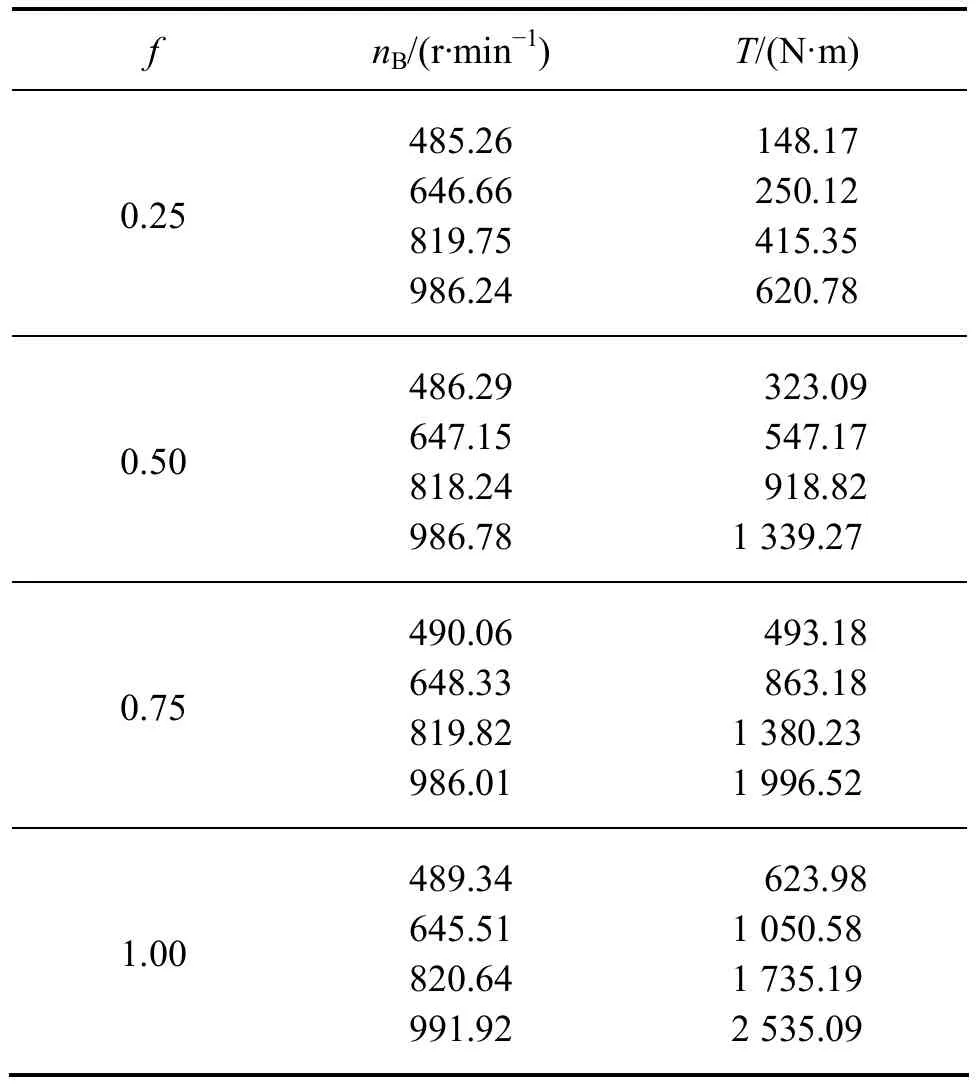
表2 试验数据结果Table 2 Experimental data results

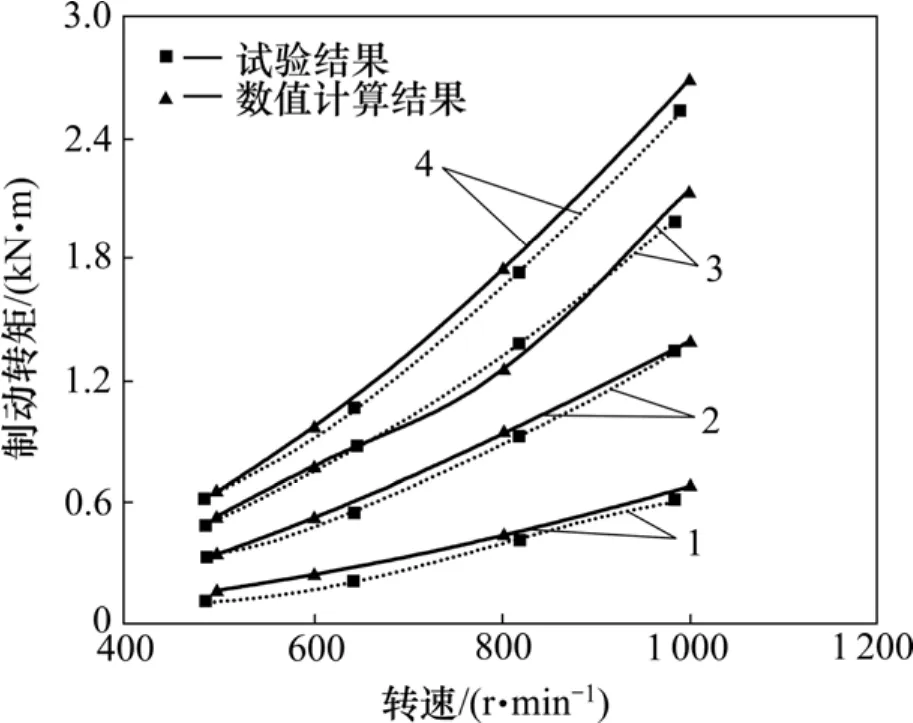
图10 数值计算结果与试验结果对比Fig.10 Comparison of numerical results with experiments

5 结论

(1) 通过定性对比发现，采用大涡模拟法，并利用滑动网格理论处理定-转子之间的流动参数传递，可以较准确地模拟液力缓速器内气-液两相流场的真实流动状态，并预测其性能。

(2) 外特性数值计算结果与试验结果吻合良好，因此可以用软件计算来代替部分试验工作，其结果可用于液力缓速器的设计及其结构优化。

[1]何仁. 汽车辅助制动装置[M]. 北京: 化学工业出版社, 2005:19-21.HE Ren. Automotive auxiliary braking system[M]. Beijing:Chemical Industry Press, 2005: 19-21.

[2]何延东, 马文星, 刘春宝. 液力偶合器部分充液流场数值模拟与特性计算[J]. 农业机械学报, 2009, 40(5): 24-28.HE Yan-dong, MA Wen-xing, LIU Chun-bao. Numerical simulation and characteristic calculation of hydrodynamic coupling[J]. Transaction of CSAM, 2009, 40(5): 24-28.

[3]严军, 何仁, 鲁明. 液力缓速器变叶片数的三维数值模拟[J].江苏大学学报: 自然科学版, 2009, 30(1): 27-31.YAN Jun, HE Ren, LU Ming. Numerical simulation of hydraulic retarder with different blade number[J]. Journal of Jiangsu University: Natural Science Edition, 2009, 30(1): 27-31.

[4]张德生, 赵继云, 刘立宝, 等. 基于 CFD 的桃形腔偶合器流场分析及结构优化[J]. 中国矿业大学学报, 2010, 39(5):687-692.ZHANG De-sheng, ZHAO Ji-yun, LIU Li-bao, et al. Flow field analysis and structure optimization of peach shaped chamber hydrodynamic coupling based on CFD[J]. Journal o f China University of Mining & Technology, 2010, 39(5): 687-692.

[5]才委, 马文星, 褚亚旭, 等. 液力变矩器导轮流场数值模拟与试验[J]. 农业机械学报, 2007, 38(8): 11-14.CAI Wei, MA Wen-xing, CHU Ya-xu, et al. Numerical simulation and experimental research on flow field in the stator of a torque converter[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(8): 11-14.

[6]Brandt T T. Usability of explicit filtering in large eddy simulation with a low-order numerical scheme and different subgrid-scale models[J]. International Journal for Numerical Methods in Fluids, 2008, 57(7): 905-928.

[7]ZHANG Yan-hong, YANG Chao, MAO Zai-sha. Large eddy simulation of the gas-liquid flow in a stirred tank[J]. AICHE Journal, 2008, 54(8): 1963-1974.

[8]Grigoriadis D G E, Bartzis J B, Goulas A. Efficient treatment of complex geometries for large eddy simulations of turbulent flows[J]. Computers and Fluid, 2004, 33(2): 201-222.

[9]王福军. 计算流体动力学分析—CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004: 139-142.WANG Fu-jun. Computational fluid dynamics analysis:Principle and application of CFD software[M]. Beijing: Tsinghua University Press, 2004: 139-142.

[10]Felten F, Fautrelle Y, Du Terrail Y, et al. Numerical modeling of electrognetically-riven turbulent flows using LES methods[J].Applied Mathematical Modelling, 2004, 28(1): 15-27.

[11]Feiz A A, Ould-Rouis M, Lauriat G. Large eddy simulation of turbulent flow in a rotating pipe[J]. International Journal of Heat and Fluid Flow, 2003, 243(3): 412-420.

[12]FLUENT Inc. FLUENT user’s guide[M]. Fluent Inc, 2003:239-244.

[13]Mary I, Sagaut P. Large eddy simulation of flow around an airfoil near stall[J]. AIAA Journal, 2002, 40(6): 1139-1145.

[14]Julian R E, Smolarkiewicz K. Eddy resolving simulations of turbulent solar convection[J]. International Journal for Numerical Method in Fluids, 2002, 39(9): 855-864.

[15]Bai L, Fieblg M, Mitra N K. Numerical analysis of turbulent flow in fluid couplings[J]. ASME Journal of Fluids Engineering,1997, 119(3): 569-576.