剪切波沿钢筋纵向入射时钢筋与混凝土间黏结力拟静力解析解
匡健,谢超,刘又文
(1. 广东省建东工程监理有限公司,广东 广州,510500;2. 湖南大学 机械与运载工程学院, 湖南 长沙,410082)
黏结是钢筋和混凝土形成整体、共同工作的基础,其实质是钢筋与混凝土接触面上所产生的沿钢筋纵向的剪应力,即通常所说的黏结应力。钢筋混凝土的黏结应力和滑移是钢筋混凝土结构理论的基本问题,它不仅是裂缝和变形研究的基础,也是有限元分析中不可缺少的内容。蒋德稳等[1-2]通过拔出型实验验证钢筋与混凝土之间黏结力与滑移量的线性本构模型,实验结果表明:在各级荷载下,钢筋上多个结点的滑移量理论值与实验值相吻合,误差很小,说明线性本构模型可以方便地运用于工程实际中。吴庆等[3]通过对混凝土试块中不同直径和保护层厚度的变形钢筋和光面钢筋进行拔出试验, 得到了不同类型试件的平均黏结应力-平均滑移关系曲线,描述了各种试件的破坏过程,对锈蚀钢筋混凝土黏结性能退化机理进行了分析,阐述了不同加速锈蚀方法、锈蚀程度、钢筋直径、保护层厚度以及箍筋等因素对钢筋与混凝土黏结性能的影响,与本文理论分析的结果规律一致。另有大量理论及实验研究[4-10]表明:各种钢筋与混凝土的黏结应力和滑移量是随界面上位置而变化的,且受到不同外荷载形式及钢筋混凝土结构的影响。许多钢筋混凝土结构因承受重复荷载作用而导致整体刚度下降、裂缝扩展、混凝土疲劳破坏、钢筋(光圆钢筋或变形钢筋)与混凝土间黏结力退化以及相对滑移增长等原因导致整个结构失效。因此,研究钢筋与混凝土间黏结力及相对滑移与钢筋混凝土结构的影响规律是非常重要的。抗震问题已经成为城市工程抗震和防灾减灾研究的重要组成部分, 在地层中一些地下钢筋混凝土工程结构发生较大变形和位移的部位可能会出现严重的地震损坏,因此,对其抗震问题应给予高度重视。在此,本文作者基于拟静力假设[11],从剪切波沿钢筋纵向入射时钢筋混凝土的弹性响应入手进行研究,虽不能获得结构地震反应的时间历程,但能够解得地震中混凝土剪应变最大时刻的结构响应,对求解钢筋混凝土黏结力和滑移量的极限值是一种简单实用的方法;结合弹性复势方法[12-14]获得剪切波纵向入射时钢筋混凝土黏结力及滑移量的封闭解析解,获得黏结力及滑移量随界面上不同点角度变化的数值曲线,并分析钢筋直径、动剪切模量、保护层厚度及箍筋直径与间距对黏结力及滑移量的影响规律。
1 模型的提出与求解
图1所示为钢筋混凝土单元,其中:无穷大基体Ⅱ为混凝土,圆柱形夹杂体Ⅰ为钢筋;当剪切波纵向入射时,γff为自由场中混凝土结构中的最大剪应变,μs为与之相应的动剪切模量。原问题被简化成为1个反平面剪切问题。
运用弹性平面复势方法并参考文献[13],假设

应力分量可表示为:
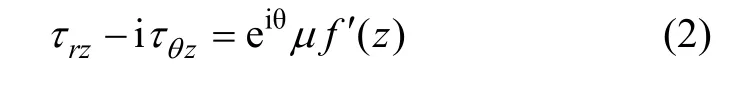
其中:w为纵向位移;τrz和τθz为沿钢筋纵向的切应力。
定义区域Ⅰ和Ⅱ的应力函数分别为:
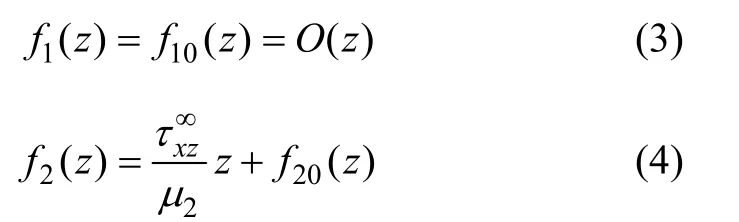
其中:
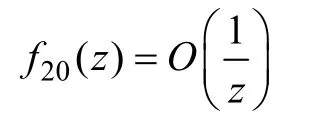
其一阶微分形式为:
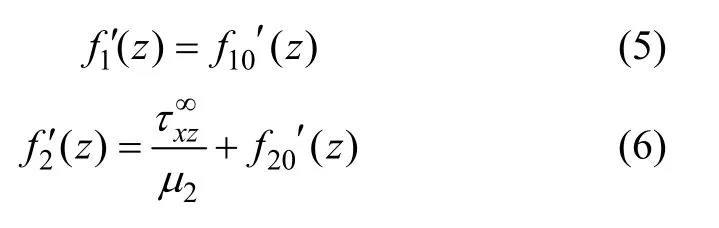
其中:
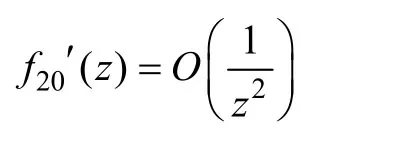
定义辅助应力函数为:
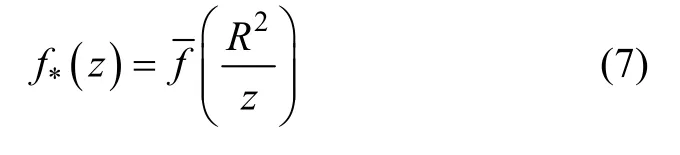
一阶微分形式为:
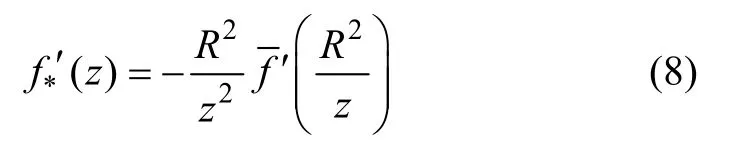
其中:R为钢筋半径。相应的区域Ⅰ辅助应力函数可表示为:
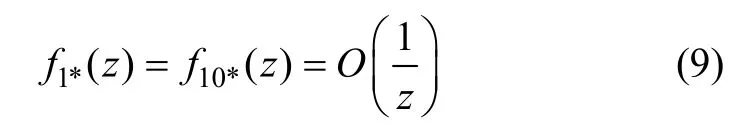
一阶微分形式为:
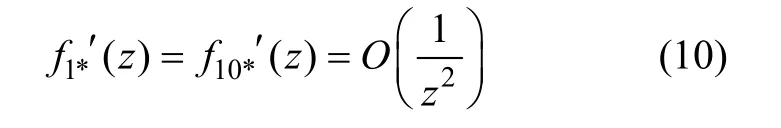
相应的区域Ⅱ辅助应力函数可表示为:
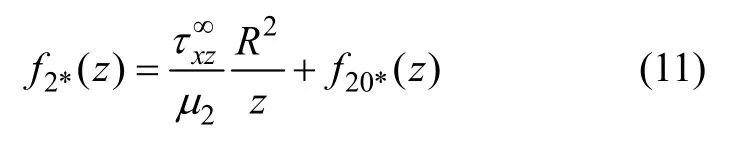
其中:
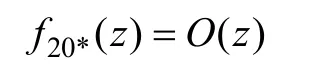
一阶微分形式为:
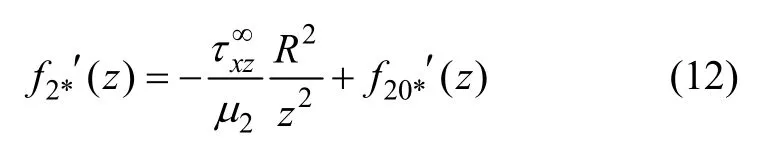
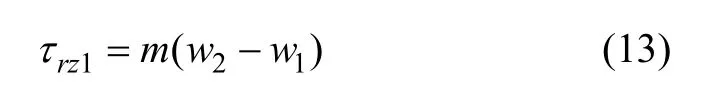
界面应力连续条件为:

将式(5),(6),(10)和(12)代入式(2)和式(14),则表示为:

将式(15)中奇性主部移至方程右边得:
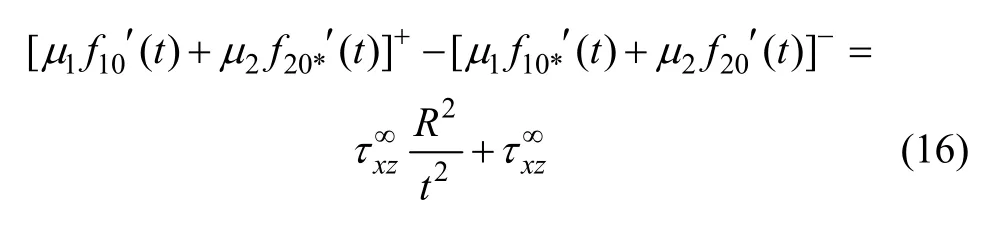
运用Plemej公式可得以下2个积分:
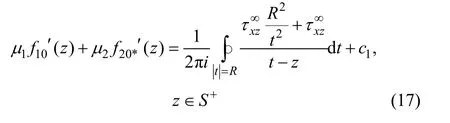
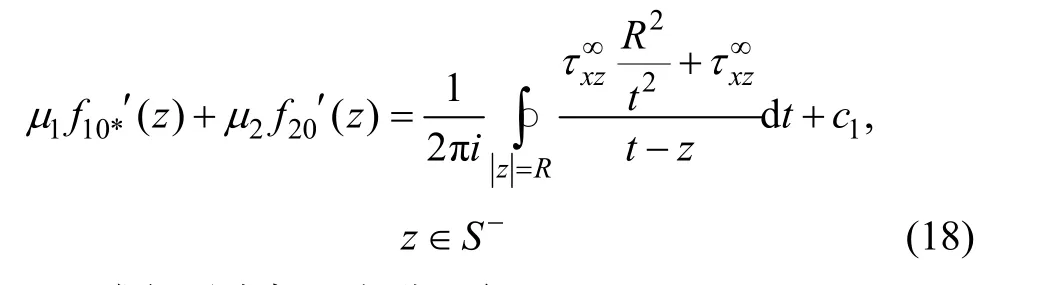
求解以上柯西积分可得:
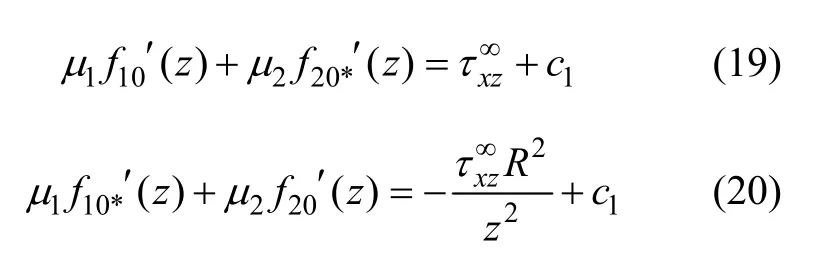
根据式(20),经比较可得c1=0。考虑线性滑移边界条件(13)式,可得:
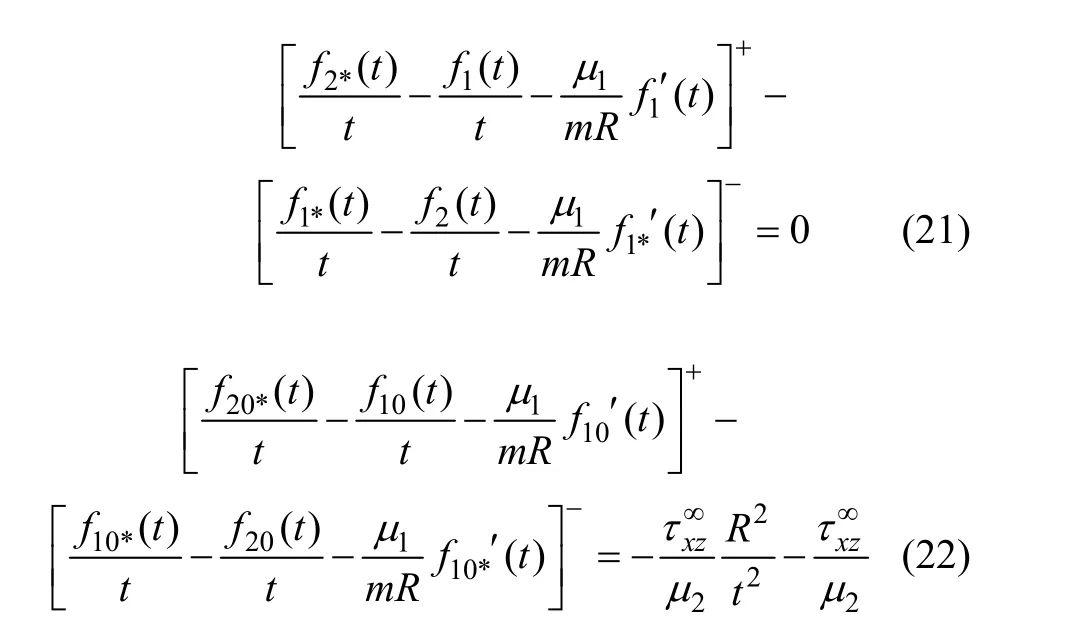
运用Plemej公式可得:
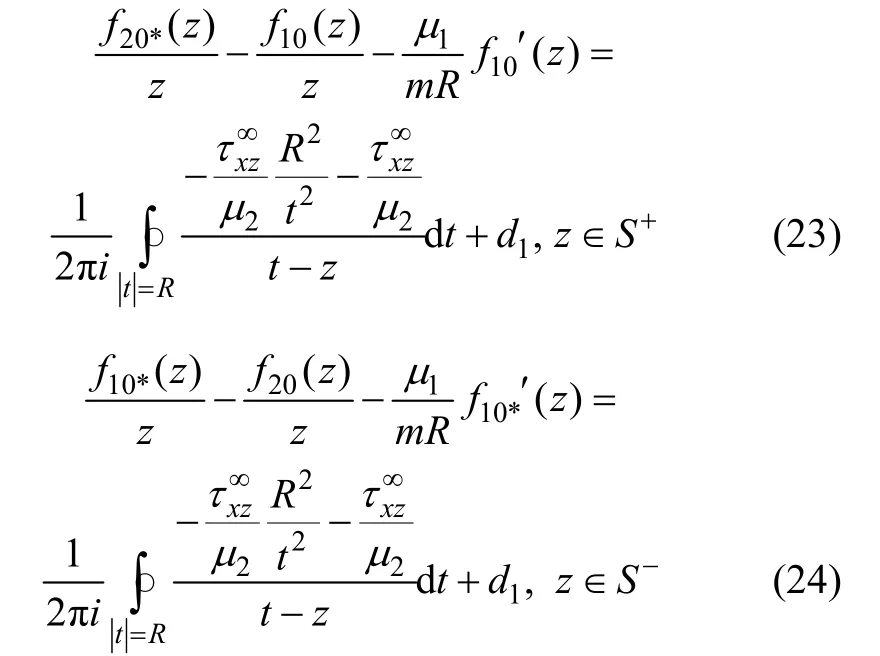
求得以上柯西积分的解为:
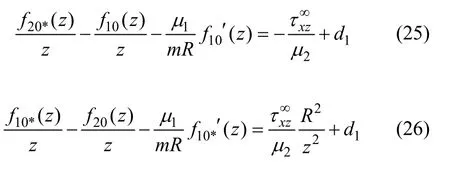
根据(26)无远处比较可得d1=0。联立式(20)与(26)可得应力函数:
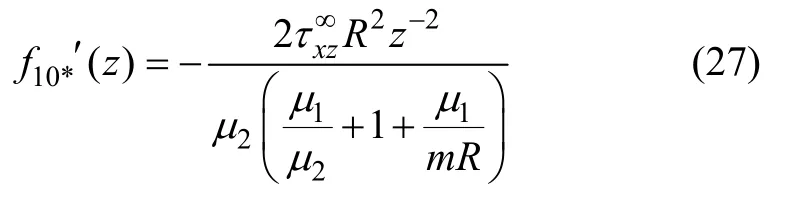
将式(27)代入式(20)可得:
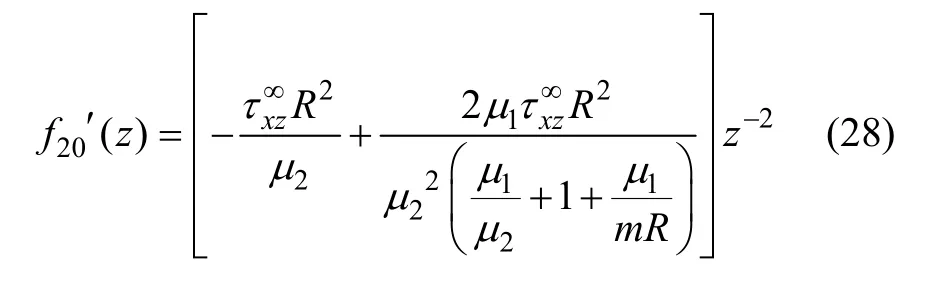
联立式(19)和(25),可得应力函数:
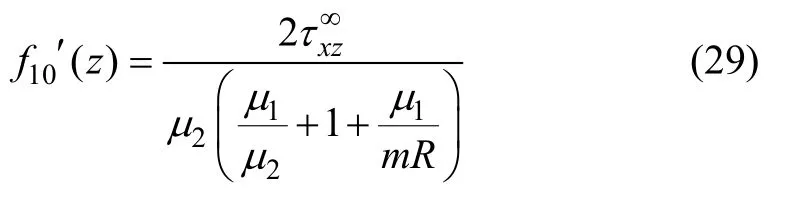
将式(29)代入式(19),可得:
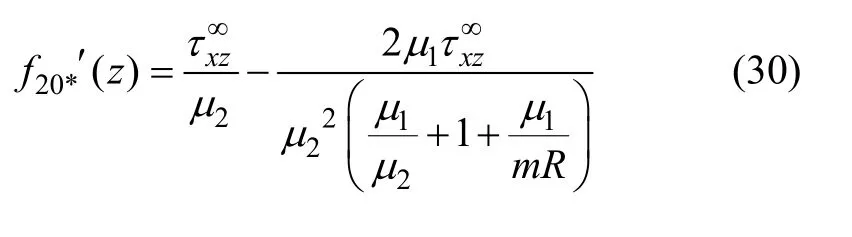
钢筋与混凝土界面滑移应力与滑移量的弹性解析解可表示为:
2 算例分析与讨论
设截面面积为250 mm×250 mm的钢筋混凝土构件中混凝土强度为C40,混凝土轴心抗拉强度ft=1.71 MPa,弹性模量E2=32.5 GPa,泊松比ν2=0.2,钢筋型号为HRB335,钢筋抗拉强度fy=300 MPa,弹性模量E1=200 MPa,泊松比ν1=0.3。文献[15]中对混凝土材料进行的动力试验表明,混凝土的动弹量比静弹模量高 30%~50%。采用以上数据并结合式(31)和(32)对钢筋与混凝土界面上的黏结力及滑移量进行数值分析。
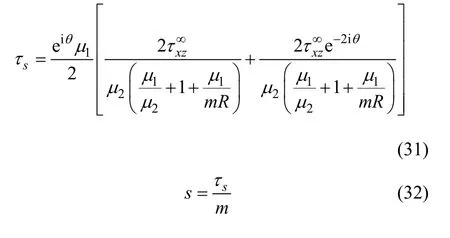
当混凝土保护层厚度为c=25 mm,采用双肢箍筋φ8@100 mm,动剪切模量为1.3倍静剪切模量时,不同直径的钢筋对钢筋与混凝土界面上不同点的黏结力及滑移量的影响曲线如图2和3所示。从图2和图3可以看出:当选用的钢筋直径越小时,钢筋与混凝土间黏结力越大,而滑移越小;钢筋直径越大,则钢筋与混凝土间黏结力越大,而滑移越大。
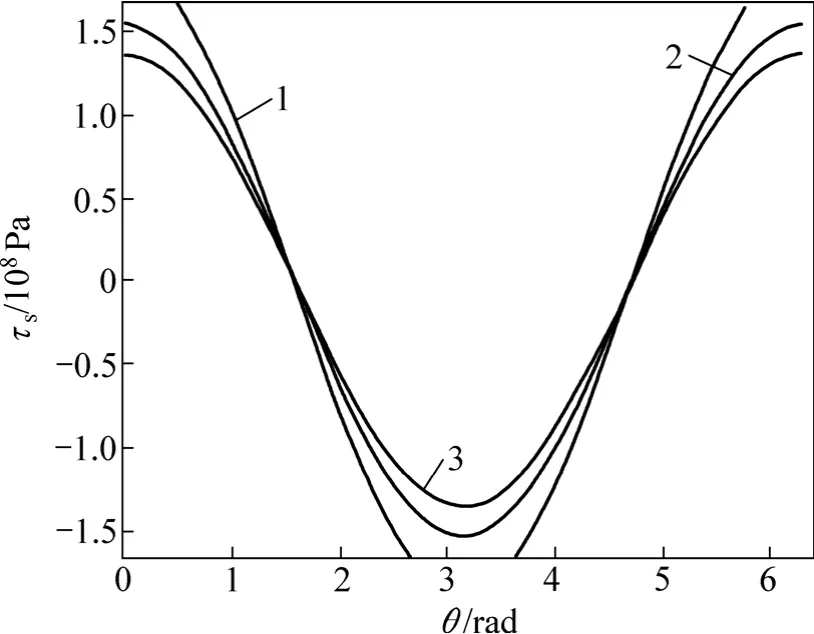
图2 不同直径d的钢筋对钢筋与混凝土界面上不同点的黏结力τs的影响曲线Fig.2 Influence curves of bond stress between rebar and concrete with different diameters of rebar
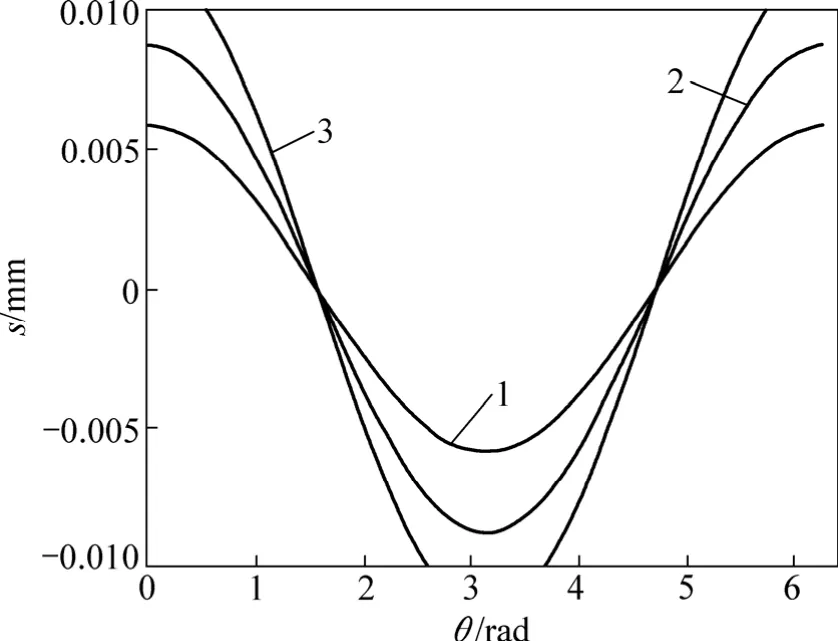
图3 不同直径d的钢筋对钢筋与混凝土界面上不同点的滑移量s的影响曲线Fig.3 Influence curves of slip between rebar and concrete with different diameters of rebar
当混凝土保护层厚度c=25 mm,钢筋直径d=8 mm时,采用双肢箍筋φ8@100 mm,不同动剪切模量对钢筋与混凝土界面上不同点的黏结力及滑移量的影响曲线如图4和图5所示。从图4和图5可以看出:当动剪切模量越大时,钢筋与混凝土间黏结力及滑移量都越大; 动剪切模量越小,则钢筋与混凝土间黏结力及滑移量都越小。
当钢筋直径为d=8 mm,采用双肢箍筋φ8@100 mm,动剪切模量为1.4倍静剪切模量时,不同混凝土保护层厚度对钢筋与混凝土界面上不同点的黏结力及滑移量的影响曲线如图6和图7所示。从图6和图7可以看出:混凝土保护层越厚时,钢筋与混凝土间黏结力越大,混凝土保护层越薄,则钢筋与混凝土间黏结力越小,而滑移量却没有明显变化。
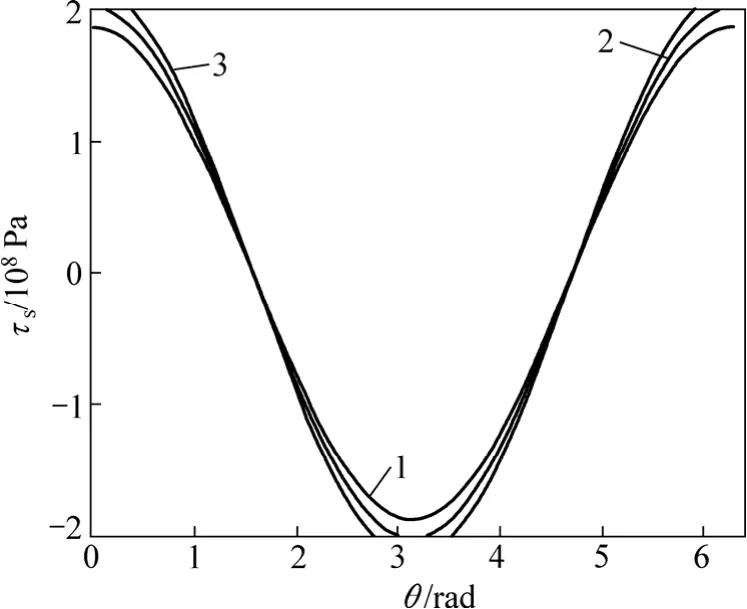
图4 不同动剪切模量μs对钢筋与混凝土界面上不同点的黏结力τs的影响曲线Fig.4 Influence curves of bond stress between rebar and concrete with different dynamic shear modulus
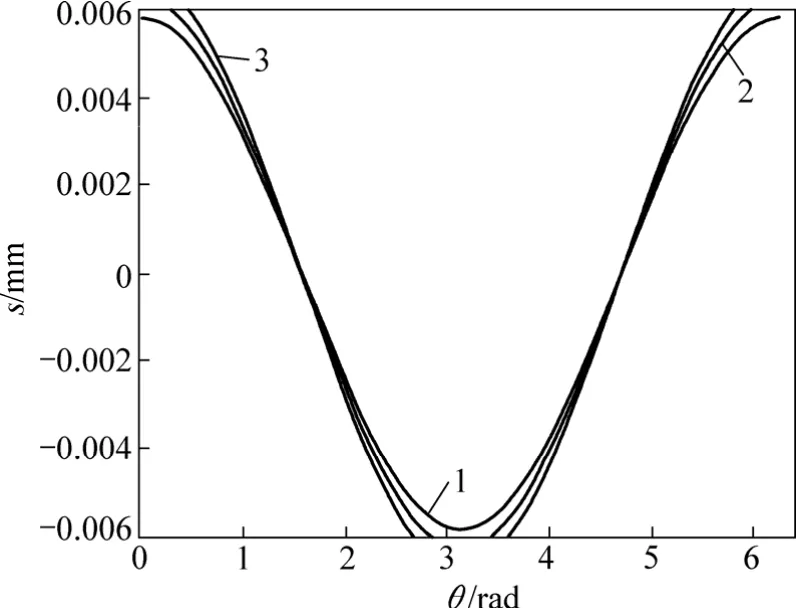
图5 不同动剪切模量μs对钢筋与混凝土界面上不同点的滑移量的影响曲线Fig.5 Influence curves of slip between rebar and concrete with different dynamic shear modulus
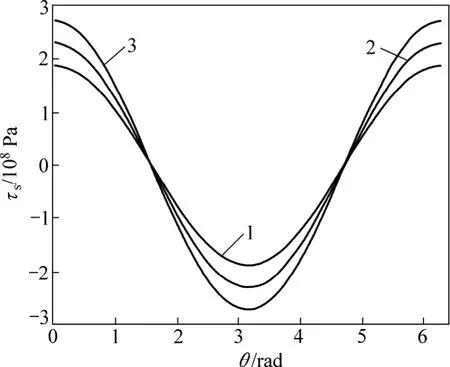
图6 不同混凝土保护层厚度c对钢筋与混凝土界面上不同点的黏结力τs的影响曲线Fig.6 Influence curves of bond stress between rebar and concrete with different thicknesses of concrete cover
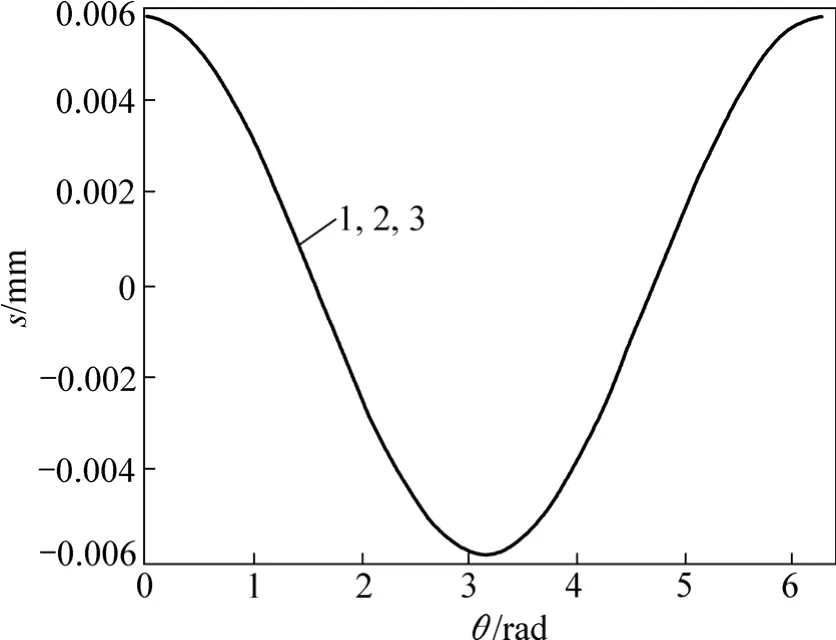
图7 不同混凝土保护层厚度c对钢筋与混凝土界面上不同点的滑移量s的影响曲线Fig.7 Influence curves of slip between rebar and concrete with different thicknesses of concrete cover
当混凝土保护层厚度为 25 mm,钢筋直径为 8 mm,采用双肢箍筋φ8@lmm,动剪切模量为1.3倍静剪切模量时,不同箍筋间距对钢筋与混凝土界面上不同点的黏结力及滑移量的影响曲线如图8和图9所示。从图8和图9可以看出:箍筋间距对黏结力及滑移量的影响很微弱。
当混凝土保护层厚度为 25 mm,钢筋直径为 8 mm,采用双肢箍筋φD@100 mm,动剪切模量为 1.3倍静剪切模量时,不同箍筋直径对钢筋与混凝土界面上不同点的黏结力及滑移量的影响曲线如图10和图11所示。从图10和图11可以看出:箍筋直径越大,黏结力越大;箍筋直径越小,则黏结力减小,而滑移量没有明显变化。
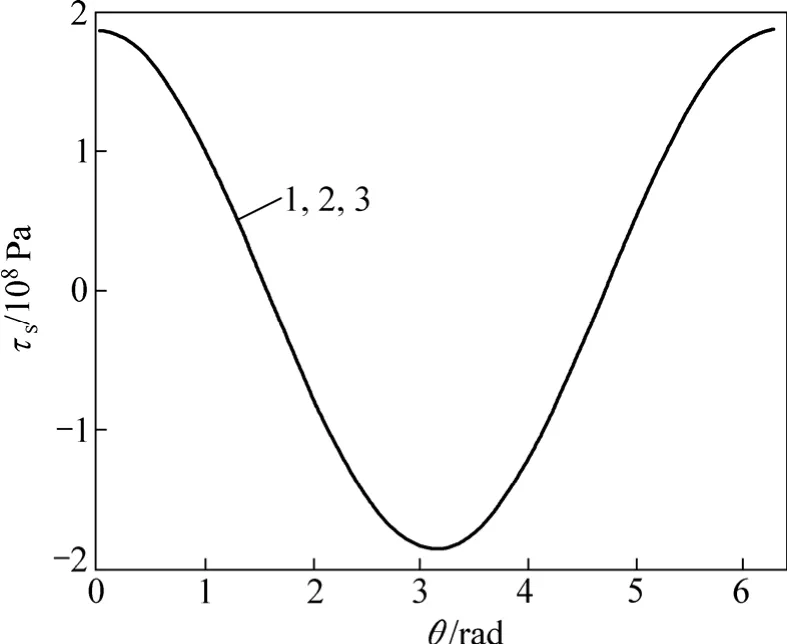
图8 不同箍筋间距l对钢筋与混凝土界面上不同点的黏结力τs的影响曲线Fig.8 Influence curves of bond stress between rebar and concrete with different spacings of stirrup
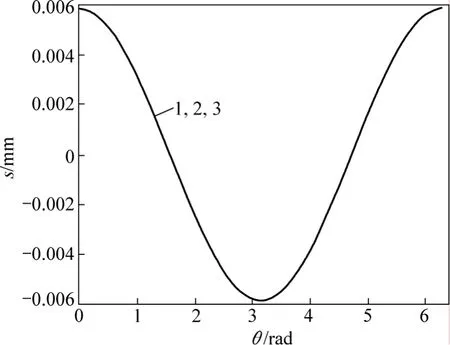
图9 不同箍筋间距l对钢筋与混凝土界面上不同点的滑移量s的影响曲线Fig.9 Influence curves of slip between rebar and concrete with different spacings of stirrup
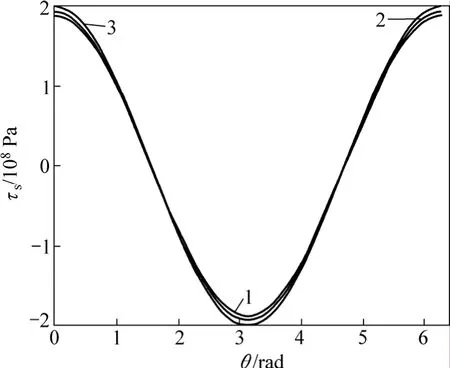
图10 不同箍筋直径D对钢筋与混凝土界面上不同点的黏结力τs的影响曲线Fig.10 Influence curves of bond stress between rebar and concrete with different diameters of stirrup
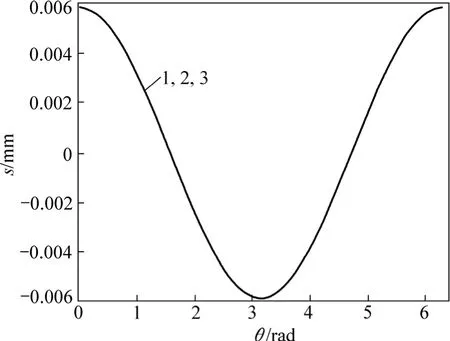
图11 不同箍筋直径D对钢筋与混凝土界面上不同点的滑移量s的影响曲线Fig.11 Influence curves of slip between rebar and concrete with different diameters of stirrup
3 结论
(1) 当选用的钢筋直径越小时,钢筋与混凝土间黏结力越大,而滑移量越小;钢筋直径越大,则钢筋与混凝土间黏结力越大,而滑移量越大。
(2) 当动剪切模量越大时,钢筋与混凝土间黏结力及滑移量都越大;动剪切模量越小,则钢筋与混凝土间黏结力及滑移量越小。
(3) 当混凝土保护层越厚时,若钢筋与混凝土间黏结力越大,混凝土保护层越薄,则钢筋与混凝土间黏结力越小,而滑移量没有明显变化。
(4) 箍筋间距对黏结力及滑移量的影响都很微弱。
(5) 当箍筋直径越大时,黏结力越大;箍筋直径越小,则黏结力越小,而滑移量没有明显变化。
(6) 本文所采用的钢筋与混凝土之间滑移的线性本构模型可合理运用到实际工程中, 而通过平面线弹性力学所获得黏结力及滑移量封闭形式解答亦可供钢筋混凝土结构设计参考。
[1]蒋德稳, 邱洪兴. 拔出型试验钢筋与混凝土间滑移量的简化解法[J]. 东南大学学报,2009, 39(4): 831-834.JIANG De-wen, QIU Hong-xing. Simplified solution of the slip between rebar and concrete based on pull-out test[J]. Journal of Southeast University, 2009, 39(4): 831-834.
[2]赵羽习, 金伟良. 钢筋与混凝土黏结本构关系的试验研究[J].建筑结构学报, 2002, 23(1): 32-37.ZHAO Yu-xi, JIN Wei-liang. Experimental study on bond constitutive relation between rebar and concrete[J]. Journal of Building Structures, 2002, 23(1): 32-37.
[3]吴庆, 袁迎曙, 蒋建华, 等. 锈蚀钢筋与混凝土黏结机理试验研究[J]. 中国矿业大学学报, 2009, 38(5): 685-691.WU Qin, YUAN Yin-shu, JIANG Jian-hua, et al. Experimental research on the bonding between corroded reinforcement bar and concrete[J]. Journal of China University of Mining and Technology, 2009, 38(5): 685-691.
[4]Balazs G L. Cracking analysis based on slip and bond stress[J].ACI Material Journal, 1993, 90(4): 340-348.
[5]Ayoub A, Filippou F C. Mixed formulation of bond-slip problems under cyclic loads[J]. Journal of Structural Engineering,1999, 125(6): 661-671.
[6]Russo G, Pauletta M. A simple method for evaluating the maximum slip of anchorages[J]. Materials and Structures, 2006,39(10): 533-546.
[7]Byung H O, See H K. Advanced crack with analysis of reinforced concrete beams under repeated loads[J]. Journal of Structural Engineering, 2007, 133(3): 422-420.
[8]Somayaji S, Shan S P. Bond stress versus slip relation-ship and cracking response of tension member[J]. Proceedings of ACI Journal, 1981, 78(3): 217-224.
[9]Cosenza E, Manfredi G, Rdeakfonzo R. Development length of FRP straight rebar[J]. Composites: Part B, 2002, 33(2): 493-504.
[10]牟晓光, 王清湘, 司炳君. 重复荷载下高强钢筋与混凝土黏结性能的试验研究[J]. 土木工程学报, 2006, 39(8): 1-6.MOU Xiao-guang, WANG Qing-xiang, SI Bing-jun. An experimental study of the bonding behavior between high-strength steel bar and concrete under repeated loadings[J].China Civil Engineering Journal, 2006, 39(8): 1-6.
[11]张栋梁, 杨林德, 谢永利, 等. 盾构隧道抗震设计计算的解析解[J]. 岩石力学与工程学报,2008, 27(3): 544-549.ZHANG Dong-liang, YANG Lin-de, XIE Yong-li, et al.Analytical solution for aseismic design calculation of shield tunnels[J]. Chinese journal of Rock Mechanics and Engineering,2009, 27(3): 544-549.
[12]Muskhelishvili N I. Some basic problems of the mathematical theory of elasticity[M]. Groningen, Holland: Noordhoff Ltd,1953: 64-123.
[13]Xie, C, Liu, Y W, Fang, Q H, et al. Cracking characteristics of mixed mode dislocations near a lip-like mode crack[J].Theoretical Applied Fracture Mechanics, 2009, 51(2): 139-143.
[14]Liu Y W, Xie C, Jiang C Z, et al. Analytical solution for a strained reinforcement layer bonded to lip-shaped crack under remote mode III uniform load and concentrated load[J]. Applied Mathematics and Mechanics, 2010, 31(9): 1125-1140.
[15]郑永来, 周橙, 黄炜, 等. 动态弹性模量的实验研究[J]. 河海大学学报, 1998, 26(2): 31-35.ZHENG Yong-lai, ZHOU Cheng, HUANG Wei. Experimental study on dynamic elastic modulus[J]. Journal of Hohai University, 1998, 26(2): 31-35.

