高频地波雷达射频干扰分离方法研究
王 赞 陈伯孝 张各各
(西安电子科技大学 雷达信号处理重点实验室,陕西 西安710071)
引 言
高频地波雷达在工作时经常受到短波通信、广播等射频干扰(RFI)的影响,严重降低了其工作性能。针对射频干扰的各种特性,国内外学者提出了一系列抑制方法,如自适应空域滤波或相干旁瓣对消[1-2]、借助水平极化辅助天线的空间极化滤波[3-4]、基于特征子空间的正交投影[5-6]、时域剔除和线性预测插值[7]及射频干扰时域和距离域抑制方法[8],在一定程度上减轻了射频干扰对高频地波雷达的影响,但它们同时也存在一些缺陷,如空域处理会因干扰的空间非平稳性会降低算法性能,且对于小型阵列雷达,空域自适应处理可能导致目标方向响应的畸变;时域剔除和线性预测插值法一般适合射频干扰较弱的白天,对于常出现于夜间的射频干扰[15],由于其强度大且出现时间占据调频周期的大部分,从而导致抑制效果变差,因此,如何减少这些射频信号对雷达的干扰以保证目标信息的准确提取是高频地波雷达的重要研究课题之一。
独立分量分析[9](ICA)由 Pierre Comon于1994年提出,是一种新的多维数字处理技术,该技术能把传感器接收到的混合信号通过ICA分析进行重构,将混合信号中的各信号分量分离出来。近年来经过许多学者的研究和改进,ICA已成为盲信号处理领域中的主流算法之一,并广泛应用于数字通信、生物医学和图像处理等领域。在雷达领域,ICA已经应用于SAR图像处理和DOA估计等方面。
常规ICA算法有应用条件的限制,只能在接收通道个数M不少于信号源个数N的情况下对混合信号实现分离。大型阵列高频地波雷达通常满足这个应用条件,因此,ICA可直接用于雷达回波的信号分量分离,但小型阵列高频地波雷达接收端天线个数少,极端情况下可能只有单根接收天线[10],通常不满足这个应用条件,导致ICA算法不能用于该类型的高频地波雷达。本文提出的ICA干扰分离方法突破了以往文献中ICA算法应用条件限制,将ICA算法应用于小型阵列高频地波雷达,在定义了信号伪周期性的基础上,利用目标回波和射频干扰分别具有伪周期性和广义周期性、高频地波雷达能够进行长时间相干积累等特点,在慢时间维把目标回波与射频干扰分离,并对分离出来的目标回波作进一步处理得到目标的距离信息和速度信息。
1 理论分析
假设高频地波雷达发射端为岸基等距线阵,发射信号为线性调频中断连续波(FMICW),接收端为安装在舰船上的单根天线。仅考虑需要分离的混合信号中只含有一个目标回波和一个射频干扰,以及高斯白噪声的情况。本节将给出目标回波信号和射频干扰信号的模型。
1.1 目标回波模型
1.1.1 目标回波模型
雷达发射信号形式[12]为
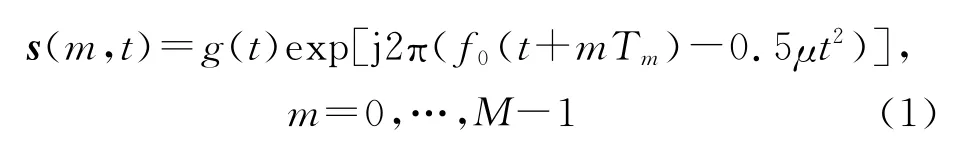
雷达接收端对接收到的回波信号经去调频、去载频、低通滤波器滤除栅瓣后,可等效为发射线性调频连续波(LFMCW)信号。则第m个调频周期低通滤波器输出的回波信号可表示为
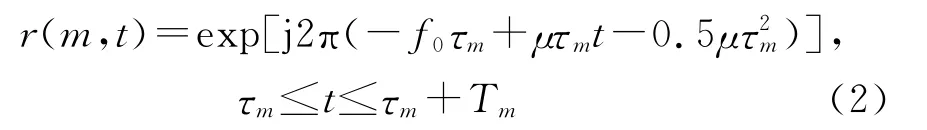
式中τm为第m个调频周期回波信号时延。
1.1.2 射频干扰模型
短波通信等射频干扰一般为窄带信号,因此,可将干扰用如下的数学模型[8]描述
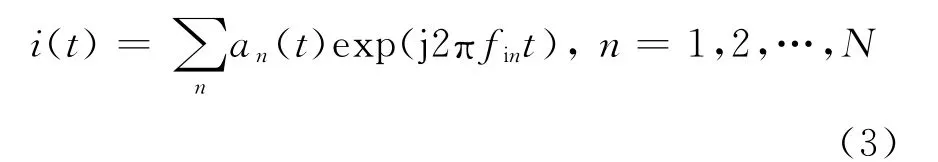
式中:an(t)和fin分别为第n个干扰的复包络和载频;an(t)一般为慢时变的随机变量。对第n个干扰进行时域分析,混频参考信号为
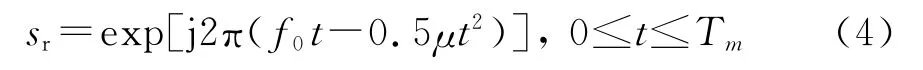
因此,第m个调频周期,混频输出的干扰信号为
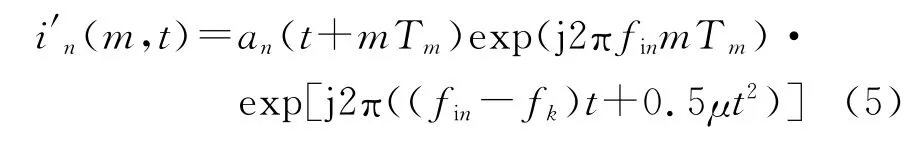
由式(5)可知混频后的射频干扰变换为线性调频信号,其调频斜率与混频参考相反。此时射频干扰频率扩展,覆盖了雷达的全频带。但经低通滤波器滤波,只有部分频率的射频干扰被保留,其他频率的干扰被滤除掉,对应到时域可得射频干扰只存在于调频周期的部分采样点。低通滤波输出的射频干扰可近似表示为
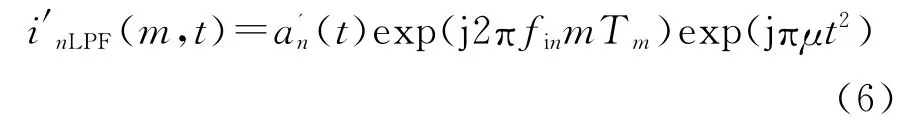
1.2 ICA算法基本原理
M个接收通道接收的混合信号xT=[x1,x2,…,xM]T,对应表示成N 个统计独立的信号源s=[s1,s2,…,sN]的线性组合

式中:[·]T表示转置;A∈CM×N为一个未知的混合矩阵,ICA的任务就是运用一种学习算法找出分离矩阵W∈CN×M,使得y=Wx=WAs,如果y=[y1,y2,…,yN]T中各分量之间相互独立,即满足WA=I,则y中的分量yi可近似认为是s中的分量sj.
根据学习算法的选取不同,可得到不同的ICA算法,常用的学习算法包括基于峭度的算法、基于负熵的算法以及自然梯度法等。采用自然梯度法[16]作为ICA的学习算法,算法的学习规则为
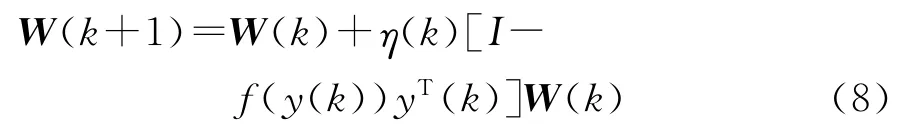
式中:k表示算法的第k次迭代;η(k)为收敛速率;W为所要估计的分离矩阵;y为混合信号各信号分量的估计值;f(y)为非线性激活函数,该函数的合理选取是学习算法收敛的关键,文献[11]详细介绍了各种非线性激活函数的特性与选择方法。
在对接收的混合信号作ICA处理之前,需要先对它作预处理[11],其中包括中心化处理和白化处理[11]。中心化处理就是混合信号减去其均值,使其变为零均值矢量,即

式中E[·]示均值。白化处理即是利用主分量分析(PCA)网络对中心化之后的混合信号x进行线性变换Q,得到v=Qx,v中各分量互不相关,Q∈CN×M为白化矩阵,N为独立信号源s的个数,M为接收到的混合信号个数。白化矩阵Q为

式中:Λ=diag(λ1,λ2,…,λN)是混合信号相关矩阵Rx=E{xxT}的N个最大特征值组成的对角阵;U∈CM×N是Λ对应的N个特征向量组成的矩阵。当M>N时,白化矩阵Q可将混合信号的维数M 阶降到N阶。经过白化处理后,原混合信号转化为

式中,B∈CN×N为新的混合矩阵,由信号源s的统计独立性可得
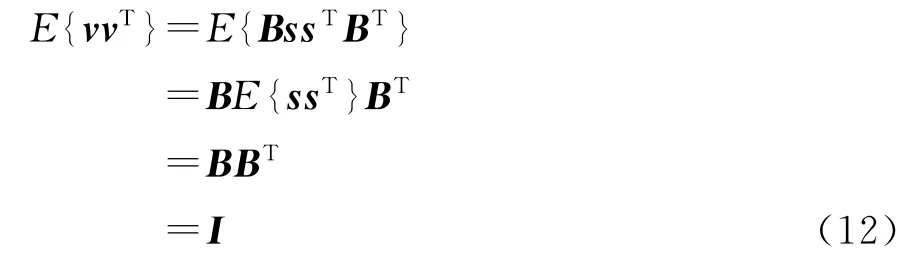
由式(12)可知新的混合矩阵B为正交矩阵,原本求分离矩阵W的问题转化为求正交分离矩阵BT的问题。因此,白化处理是通过对混合信号的奇异值分解(SVD),确定混合信号的信号分量个数、完成各信号分量去相关处理,同时降低获取各信号分量所需线性空间维数,减少ICA处理的计算量。
1.3 信号周期性分析
1.3.1 周期信号定义的拓展
文献[13]给出了周期信号的定义,即周期信号满足
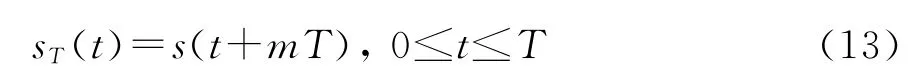
式中T为信号sT的周期。
文献[14]给出了广义周期信号的定义,即广义周期信号满足
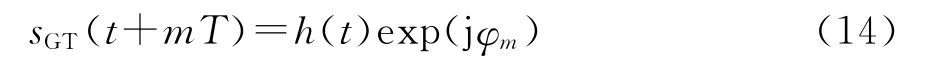
式中:h(t)为sGT在第一个周期的信号波形;φm为信号sGT的第m个周期相对于h(t)的相位差;exp(jφm)是关于周期T的慢时间项。由式(14)可知:当φm=0时,式(14)退化为式(13).可知广义周期信号是周期信号的延拓,具有更广泛的适用范围。
给出伪广义周期信号的定义,即伪广义周期信号满足
与式(14)相比,伪广义周期信号增加了exp(jφmt),该项为与慢时间m和快时间t相关的相位项。φm为此信号的第m个周期相对于h(t)的相位差,当φm=0时,式(15)退化为式(14)。可知伪广义周期信号是广义周期信号的延拓,比广义周期信号具有更广泛的适用范围。
1.3.2 目标回波周期性分析
由1.1.1节可知:经混频和低通滤波后第m个调频周期目标回波如式(2)所示,讨论目标相对于接收站为静止和匀速直线运动两种情况。
当目标相对于接收站静止时,在一个相参积累周期内任取第m1个调频周期和第m2个调频周期的目标回波,它们的比值为
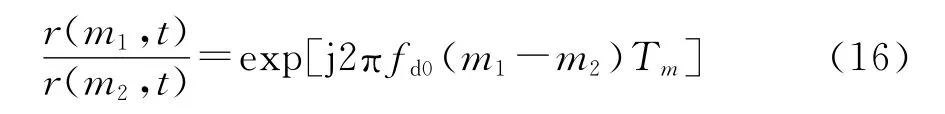
式中,由于目标等效速度为0,因此,其对应的多普勒频率fd0=0,则式(16)中r(m1,t)=r(m2,t),可知当目标相对于接收站静止时,目标回波信号是具有周期性的。
当目标相对于接收站作匀速直线运动时,在一个相参积累周期内任取第m1个调频周期和第m2个调频周期的目标回波,它们的比值为
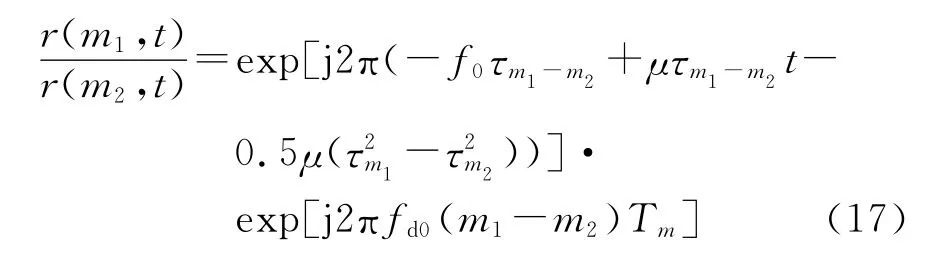
式中:τm1-m2=τm1-τm2.分析式(17)中各项,exp[j2πfd0(m1-m2)Tm]、exp(-jπμ(τ2m1-τ2m2))与exp(-j2πf0τm1-m2)为慢时间项,exp(j2πμτm1-m2t)为与慢时间m和快时间t相关的相位项。因此,目标作匀速直线运动时的第m个调频周期的回波信号可写成伪广义周期信号的形式
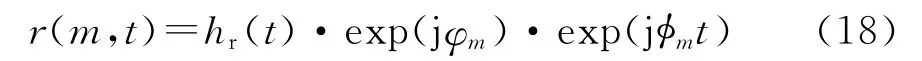
式中:
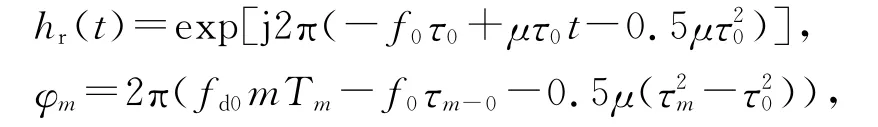
φm=2πμτm-0在m 个调频周期里φm是否近似为0,主要取决于调频斜率μ、目标等效速度˜v0以及调频周期Tm.岸-舰双基地高频地波雷达的检测目标以低速的舰船目标为主,目标最大等效速度取vmax=25m/s,调频周期Tm通常取0.5s,调频斜率μ=1e5.在上述条件下,由于目标等效速度过低,因此目标回波信号在任意相邻m0个调频周期内具有广义周期性,且目标等效速度越小,m0的取值越大。因此可以确定当目标相对于接收站作匀速直线运动时,目标回波信号具有伪广义周期性。
1.3.3 射频干扰周期性分析
由1.1.2节可知,经混频和低通滤波后第m个调频周期射频干扰如式(6)所示。在一个相参积累周期内任取第m1个调频周期和第m2个调频周期的第n个射频干扰,它们的比值为
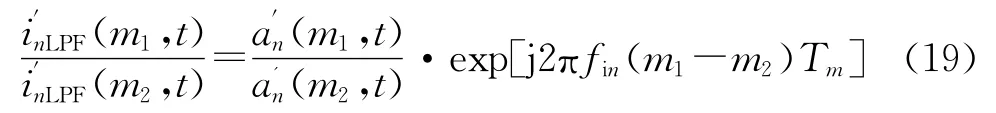
式中等号右边两项均为慢时间项,射频干扰信号具有广义周期性。把第m个调频周期的第n个射频干扰写成广义周期信号的形式
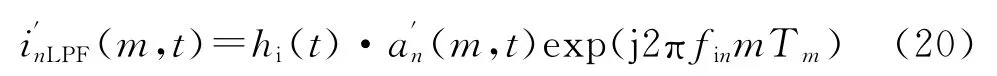
式中,hi(t)=exp(jπμt2).
1.4 ICA单通道干扰分离方法
1.4.1 方法原理
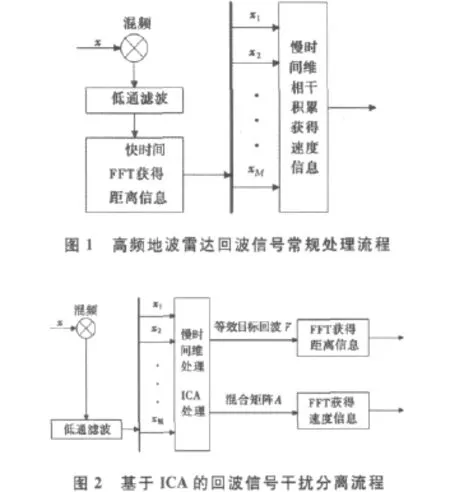
高频地波雷达能够对接收信号作长时间的相干积累,通常积累的周期数M在128~256之间(本文取M=128),令一个相干积累周期(即M 个调频周期)的回波信号表示为x=[x1,x2,…,xM],xm表示第m个调频周期的回波信号,常规的处理流程如图1所示,即雷达首先对每个调频周期的回波信号都做快时间维处理,求出目标的距离信息,然后将x构造为矩阵形式做慢时间维处理,求出目标的速度信息。由于目标回波在目标相对接收站等效静止和匀速直线运动时,分别具有周期性和伪广义周期性,射频干扰具有广义周期性,因此,本文拟对单接收通道一个相干积累周期的回波信号x作如图2所示的处理,即先构造x为矩阵形式,在慢时间维用ICA对M个调频周期的回波信号作联合处理,分离出等效目标回波并得到混合矩阵A,再分别对和其在A中对应的某一列向量作快速傅里叶变换(FFT)处理得到目标的距离信息和速度信息。
分析混合矩阵A中包含目标速度信息的原因,以及匀速运动目标的回波信号对等效目标回波个数的影响:
在ICA处理前需要对M个调频周期的回波信号作PCA白化处理以确定信号分量的个数。
1)假设回波信号中包含N个统计独立的周期信号或广义周期信号,经SVD分解后大特征值个数与信号分量个数N相同,即周期信号和广义周期信号经ICA处理得到的等效信号个数与原信号中信号分量个数一致。但由于广义周期信号各调频周期之间存在慢时间项exp(jφm)的差异,因此可以推断该项在PCA白化处理过程中成为混合矩阵A中的某一列向量。对于周期信号,由于无exp(jφm)的差异,因此,在PCA白化处理过程中周期信号对应A中的某列向量应为全1的列向量。
2)假设回波信号中只包含一个匀速运动目标的回波信号,该信号具有伪广义周期性,以式(19)的回波信号为例,在PCA白化处理过程中伪广义周期信号的慢时间项exp(jφm)成为混合矩阵A中的某一列向量,而φm中包含目标的速度信息,因此混合矩阵A中也包含了该信息。又由于伪广义周期信号各调频周期之间存在exp(jφmt)的影响,因此原有的一个信号源经SVD分解后变为多个相同的等效信号源,其个数与目标等效速度有关,速度越小个数越少,速度越大个数越多。图3说明了目标在不同运动速度下,其回波经SVD分解后得到大特征值的个数。
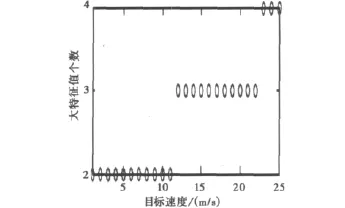
图3 目标速度与大特征值个数的对应关系
此外,因为式(19)的目标回波中还包含慢时间项exp(-j2πf0τm),该项对目标速度信息的估计有一定影响,所以在PCA和ICA处理前需对混合信号作相位补偿,消除exp(-j2πf0τm)对目标速度信息估计的影响。图2中慢时间维ICA处理步骤如下:
1)预处理混合信号x∈CM×1得到新的混合信号v∈CN×1.
2)选取N×N阶随机阵W作为初始分离矩阵(W=[w1,w2,…,wN]T).
3)选取非二次函数f(y),令n=1.
4)k=k+1,计算y(t)=wTn(k)v(t).
5)利用公式(8)给出的学习算法计算wn(k+1),利用 Gram-Schmidt正交化将wn(k+1)与w1,w2,…,wn-1,wn+1,…,wN去相关。
6)当|wn(k+1)-wn(k)|<ε时,令n=n+1,转向步骤(4),直至n=N;
7)y(t)=Wv(t),到分离信号。
8)由分离信号y和原混合信号x估计出混合矩阵A.
1.4.2 分离性能分析指标
分离性能分析主要考察分离算法恢复混合信号中各信号分量波形的程度,文献[15]给出了基于分离信号与源信号相关程度的算法性能评价准则,以分离信号yi与源信号sj的相关系数作为度量
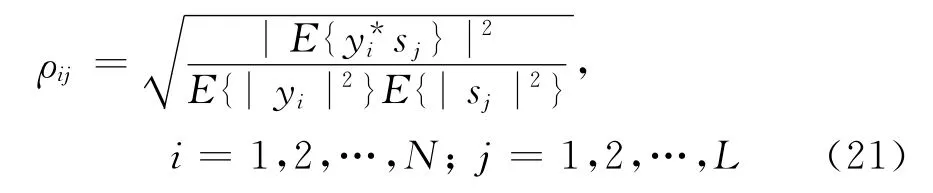
式中:ρij值越接近1,分离信号yi越接近源信号sj,即sj的波形恢复的越好;ρij值趋于0,分离信号yi与源信号sj不相关。
2 实验结果分析
假设雷达发射工作的载频为f0=6.75MHz,脉冲宽度Te=0.3ms,脉冲重复周期Tr=1ms,调频周期为0.45s,调频带宽Bm=60kHz,积累周期为128;接收回波中存在一个目标,其距离R=203 km,速度v=15m/s,一个射频干扰信号,其信号载频为6.745 173MHz,信干比为-46dB,信噪比为-10dB.
仿真实验1:本文所提ICA干扰分离方法抑制干扰的效果。实验给出了用本文方法做单通道干扰分离前后的距离维和多普勒维的功率谱,如图4和图5所示,根据仿真条件图4(a)给出了经低通滤波后某个周期回波信号以及其中各分量的时域波形。图4(b)到图4(d)为回波信号未经ICA干扰分离的距离谱、多普勒谱。可以看出目标的距离-多普勒谱比射频干扰的低10dB左右。
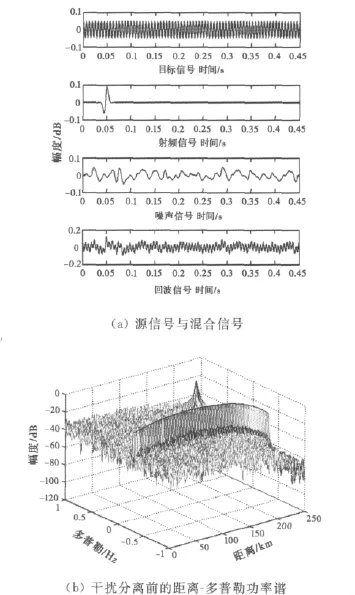
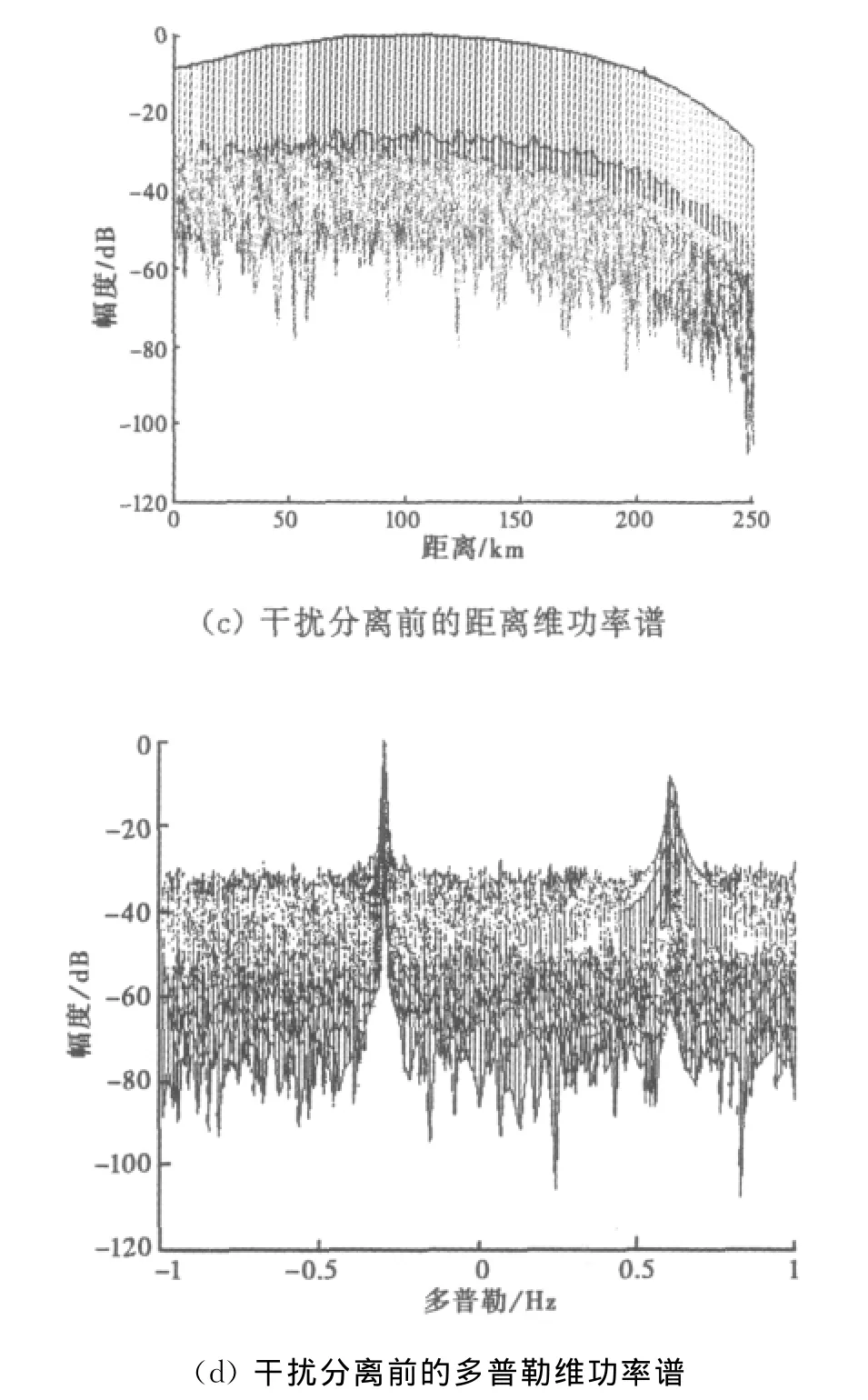
图4 射频干扰分离前的距离维和多普勒维的功率谱
图5(a)为回波信号作ICA处理之后分离出来的几个时域波形,由于目标回波信号具有伪周期性,因此分离出来与其相关的波形有3个,分别为第2、3、4个波形,第1个波形为射频干扰信号的时域波形。图5(b)到图5(d)为图5(a)中第4个分离信号的距离维与多普勒维的功率谱。可以看出图5(c)中目标距离单元前后沿的旁瓣比主瓣低了40dB,图5(d)旁瓣比主瓣低了20dB,说明经过ICA处理,射频干扰信号对目标回波的影响大大降低。
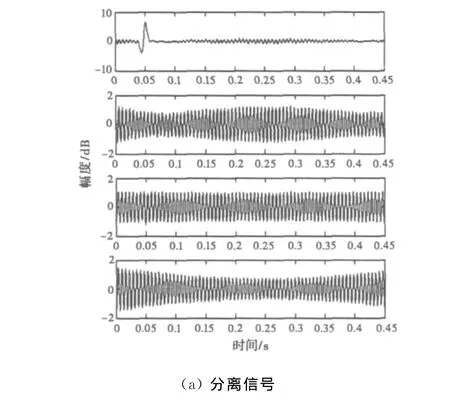
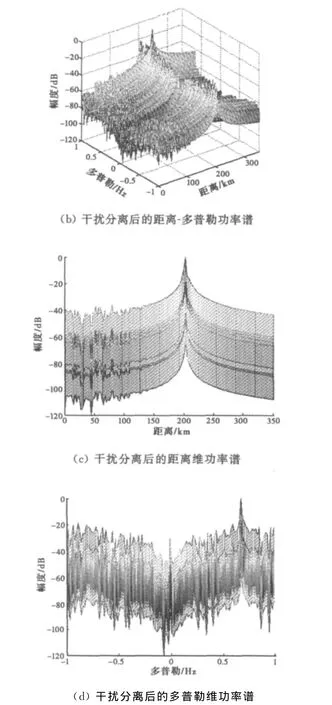
图5 利用ICA作射频干扰分离后的距离维和多普勒维的功率谱
仿真实验2:常规剔除法抑制干扰的效果。实验给出了用常规的剔除法抑制射频干扰后的距离维与多普勒维功率谱,如图6所示,由图6(b)可知,剔除法分离干扰后目标距离单元前后沿的旁瓣比主瓣低了20dB,劣于本文方法,图6(c)中旁瓣比主瓣低了20dB左右,与本文方法相当,总体来看本文方法优于常规的剔除法。
仿真实验3:性能分析。实验给出了利用式(21)对本文方法作性能分析的结果。表1所示为分离后各信号与源信号的相关系数:
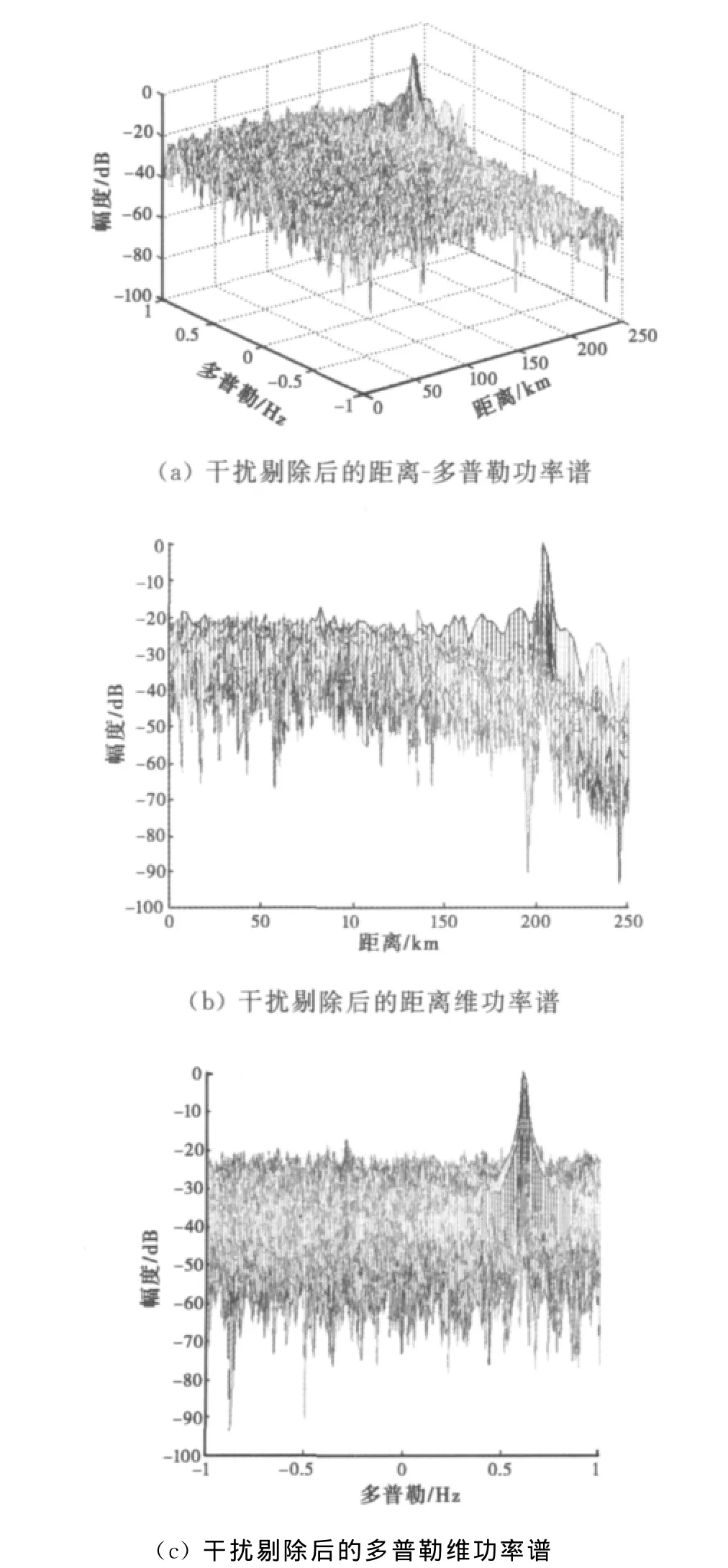
图6 利用剔除法作射频干扰分离后的距离维和多普勒维的功率谱
其中:源信号分别为目标回波、射频干扰、白噪声,ICA分离后的信号1~4分别表示图5(a)中的第1~4个信号。从表1可以看出,本文方法具有良好的分离性能,分离信号4作为目标回波信号的估计信号,其与射频干扰的分离效果最好。
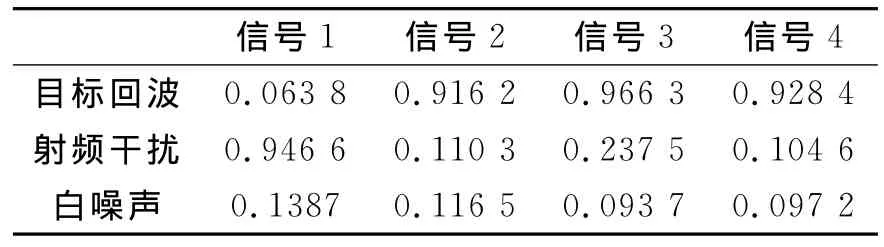
表1 分离后各信号与源信号的相关系数
3 结 论
由于常规的ICA方法要求处理通道个数大于信号源个数才能实现信号分离,不能直接用于小型阵列高频地波雷达,因此本文拓展了信号周期性的定义,提出了信号伪周期性的概念,在此基础上分析目标回波信号和射频干扰信号的周期性,并利用信号周期性以及高频地波雷达相干积累时间长的特点,在慢时间维对积累周期内M个调频周期的回波用ICA作联合处理,实现目标回波与射频干扰的分离。仿真实验证明了单通道情况下的ICA干扰分离方法的有效性。
[1]苏洪涛,保 铮,张守宏.自适应地波超视距雷达高频通信干扰抑制[J].电波科学学报,2003,18(3):270-274.SU Hongtao,BAO Zheng,ZHANG Shouhong.A-daptive HF-communication interference mitigation in HF-GWR[J].Chinese Journal of Radio Science,2003,18(3):270-274.(in Chinese)
[2]WAN Xianrong,KE Hengyu,WEN Biyang.Adaptive cochannel interference suppression based on subarrays for HFSWR[J].IEEE Signal Processing letters,2005,12(2):162-165.
[3]LEONG H.Adaptive nulling of skywave interference using horizontal dipole antennas in a coastal surveillance surface wave radar system[C]//Proc of IEEE Radar Conference.Edinburgh,October 14-16,1997:26-30.
[4]张国毅,刘永坦.高频地波雷达多干扰的极化抑制[J].电子学报,2001,29(9):1206-1209.ZHANG Guoyi,LIU Yongtan.Polarization suppression of multidisturbance in HF ground wave radar[J].Acta Elactronica Sinica,2001,29(9):1206-1209.(in Chinese)
[5]ZHOU Hao,WEN Biyang,WU Shicai.Dense radio frequency interference suppression in HF radar[J].IEEE Signal Processing letters,2005,12(5):361-364.
[6]张雅斌,陈伯孝,张守宏.舰载无源综合脉冲雷达射频干扰抑制[J].西安电子科技大学学报,2007,34(4):514-517.ZHANG Yabin,CHEN Boxiao,ZHANG Shouhong,et al.Cochannel interference suppression for the shipbased passive synthetic impulse and aperture radar[J].Journal of Xidian University,2007,34(4):514-517.(in Chinese)
[7]ZHOU Hao,WEN Biyang,WU Shicai,et al.Radio frequency interference suppression in HF radar[J].IEE Proc of Electronics Letters,2003,39(12):925-927.
[8]刘春波.岸-舰双基地高频地波SIAR相关技术研究[D].西安:西安电子科技大学,2008.LIU Chunbo.Study on Coast-ship Bistatic HF Surface Wave SIAR System and Relevant Techniques[D].Xi’an:Xidian University,2008.(in Chinese)
[9]COMON P.Independent component analysis-a new concept[J].Signal Process,1994,36(3)287-314.
[10]CHEN Baixiao,CHEN Duofang,ZHANG Shouhong.Experimental system and experimental results for coast-ship bi/multistatic ground-wave over-the-horizon radar[C]//International conference on Radar.Shanghai,October 16-19,2006:36-39.
[11]CICHOCKI A,AMARI S.自适应盲信号与图像处理[M].北京:电子工业出版社,2005.
[12]陈多芳.岸-舰双基地波超视距雷达若干问题研究[D].西安:西安电子科技大学,2008.CHEN Duofang.Study on Some Issues of Coast-Ship Bistatic Surface Wave Over-the-horizon Radar[D].Xi'an:Xidian University,2008.(in Chinese)
[13]CHENG H,TANG B,DU J J,et al.Single channel pulse train radar signal separation using algebraic method[C]//IET International Radar Conference.Guilin,April 20-22,2009:382-385.
[14]彭 耿,王丰华,黄知涛,等.单通道混合信号中周期信号的盲分离[J].湖南大学学报,2010,37(4):42-45.PENG Geng,WANG Fenghua,HUANG Zhitao,et al.Blind periodic signal separation of single channel composite signal[J].Journal of Hunan University,2010,37(4):42-45.(in Chinese)
[15]倪晋平,马远良,孙 超.用独立分量分析算法实现水声信号盲分离[J].声学学报,2002,27(4):321-326.NI Jinping,MA Yuanliang,SUN Chao.Blind separation of underwater acoustic signals via independent component analysis algorithms[J].Acta Acustica,2002,27(4):321-326.(in Chinese)
[16]AMARI S,CHEN T P,CICHOCKI A.Stability analysis of adaptive blind source separation[J].Neural Networks,1997,10(8):1345-1351.

