相干源诱偏下极化对相位干涉仪导引头测角影响研究

张 亮 徐振海 吴迪军 王雪松

（国防科技大学电子科学与工程学院，湖南 长沙410073）

引 言

反辐射导弹（ARM）具有高速、宽工作频带、高灵敏度等优点，是击毁敌方雷达设施和有源电子干扰设施的强有力武器，对雷达的生存构成了致命的威胁［1－3］。对付ARM的措施主要有以下几种：建立专门的反辐射告警系统、采用先进的雷达体制、采用雷达诱饵技术和实施硬杀伤措施［4］。其中，雷达有源诱饵技术是一种较为经济有效的对抗手段。

被动雷达导引头大都采用单脉冲测角技术，具有作用距离远、体积小、智能化高、抗干扰能力强等优点，但是由于受客观条件限制，导引头天线的波束宽度不能太窄，使得导引头角度分辨能力弱，这成为诱偏系统对抗反辐射武器的重要突破口。为了进一步提高测角精度，目前国内外的被动雷达导引头（PRS）大都采用相位干涉仪进行测向。文献［5］推导了多点源作用下合成电磁场模型，分析了有源诱偏对反辐射导弹的诱偏效果。文献［6］分析了相干源诱偏下比相PRS的测角性能，指出在相干源诱偏下PRS将跟踪雷达和诱饵的合成相位中心，跟踪角度不固定且不断变化。文献［7］分析了ARM干涉仪导引头对线性调频信号（又称为chirp信号）辐射源的测角问题。以上文献考虑了雷达和诱饵辐射场的幅度和相位对导引头测角性能的影响，但忽略了雷达、诱饵信号以及导引头接收天线的极化方式的影响。而文献［5］虽然在建模时提及了雷达和诱饵辐射场的极化方式，但在后续的分析及仿真中并未研究极化对被动导引头接收信号的影响。

根据极化电波接收理论可知，若来波极化与接收天线极化互为共轭时，天线接收功率达到最大；若来波极化与接收天线极化互为正交时，天线接收功率达到最小［8］。这体现了极化对接收信号功率的影响。另一方面，天线空域极化特性理论指出［9－12］：天线的极化方式与空间观测位置有关，并且随着空间指向的不同，同一空间位置接收到的天线辐射电磁波的极化不同。雷达天线在扫描过程中，天线辐射场的极化方式也有所不同。而诱饵天线受成本、尺寸等因素限制，一般不扫描，且为了覆盖大空域，主瓣通常很宽，其极化方式一般认为较为稳定。因此，在计算导引头天线的接收电压时，不可忽略极化的影响。

在考虑了雷达信号和诱饵信号的幅度、相位和极化方式以及导引头接收天线的极化方式的基础上，建立了相干两点源诱偏下干涉仪导引头的数学模型，并详细地分析了极化对干涉仪导引头测角性能的影响，重点关注了雷达天线极化变化对导引头测角性能的影响。

1 数学模型

1.1 信号模型

相位干涉仪原理如图1所示，天线A和天线B接收的信号经过鉴相器后得到两天线接收信号的相位差Φ，则入射角θ可用式（1）得到［13］

式中：d表示相位干涉仪基线长度；λ表示入射信号的波长。

图1 相位干涉仪的测向原理

假设构成干涉仪的天线A和天线B具有相同的增益特性和极化矢量h，诱偏系统由雷达和一个相干诱饵辐射源组成，雷达和诱饵的频率相等，入射角度分别为θ1和θ2，信号复包络为a1（t）和a2（t），极化矢量为h1和h2.则干涉仪天线阵的接收信号为

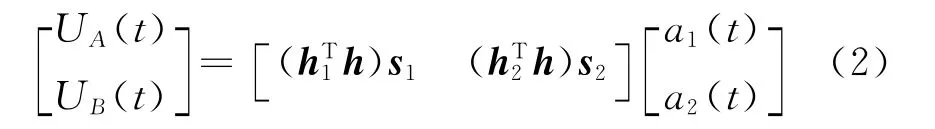
式中：s1和s2为雷达和诱饵的空域导向矢量，满足s＝ ［1，ej2πdsinθ／λ］T.由 于 诱 饵 与 雷 达 信 号 相 干，有a2（t）＝kejΔφa1（t），k和 Δφ为两信号的功率比和初始相位差，得到

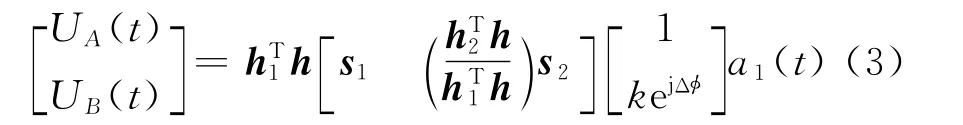
1.2 干涉仪输出相位差分析

定义两个复合因子κ和ψ为考虑极化影响后导引头天线接收的诱饵信号与雷达信号的功率比与幅度差：κ＝kξ，ψ＝Δφ＋δ，则天线A与天线B接收信号的相位差可表示为

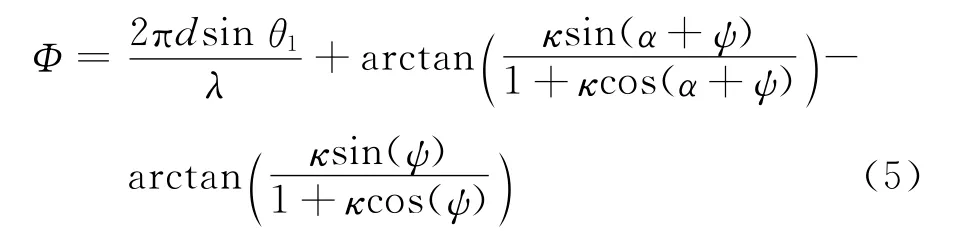
式中α＝2πd（sinθ2－sinθ1）／λ.可以看出，两天线输出的相位差是诱饵和雷达信号的幅度比k、到达角θ2和θ1、初始相位差Δφ、极化矢量h2和h1以及导引头天线的极化矢量h的函数。

2 极化对干涉仪测向的影响分析

引入庞加莱（poincare）极化球［8］，定义 mp为接收天线与来波的极化匹配系数［8］

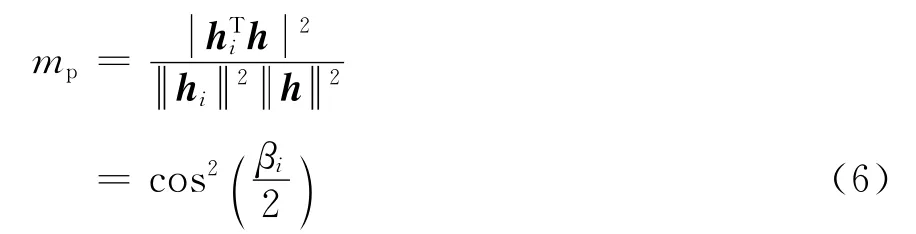
式中i＝1、2，βi为接收天线的共轭极化点h＊与来波极化点所夹的球心角。由于 h2＝ h12＝h22＝1，因此

可以看出，极化会在很大程度上影响导引头接收的两辐射源功率比κ.

一般，PRS跟踪角度总是在功率较大的辐射源附近变化［6］，其跟踪方向还与δ有关，在一定的κ下，PRS跟踪角度将随δ的变化而改变。假设雷达和诱饵的入射方向不变，即θ1、θ2固定，功率比k（k≠0、∞）和初始相位差Δφ给定，讨论极化对PRS跟踪方向的影响。

1）κ＝0时，即ξ＝0，h和h2互为交叉极化，这时Φ＝2πdsinθ1／λ，PRS跟踪雷达信号。

2）κ→∞时，即ξ＝∞，h和h1互为交叉极化，这时Φ＝2πdsinθ2／λ，PRS跟踪诱饵信号。

3）κ＝1时，即ξ＝1／k，容易得到：干涉仪输出的相位差只有两个取值，且在Δφ＋δ＝π和α＋Δφ＋δ＝π附近，Φ发生π的突变。突变点的δ满足

在突变点之外，相位差Φ ＝πd（sinθ1＋sinθ2）／λ，PRS跟踪诱饵与雷达的相位中心；在突变点之间，相位差Φ＝πd（sinθ1＋sinθ2）／λ－π.

4）在δ的取值范围内，干涉仪输出角度θ还有可能取得极值点，这时的PRS跟踪偏差最大。当κ一定时，对相位差Φ求导

由∂Φ／∂δ＝0求Φ的极值点，得到：α／2＋ψ＝nπ（n为整数），即

这时干涉仪输出的相位差为

5）κ＜1时，即ξ＜1／k，干涉仪输出角度θ在θ1附近变化。若极化矢量h、h1和h2使得δ满足

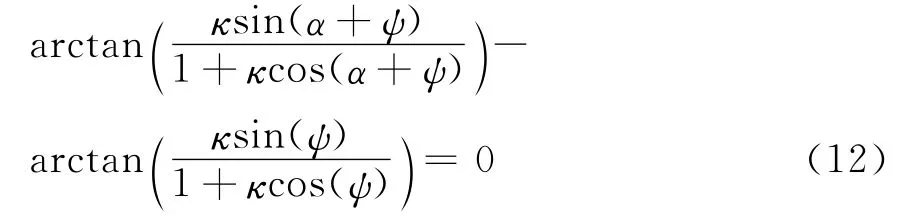
则由式（5）可得PRS跟踪雷达。这时要求m为奇数

若忽略其他因素，考虑极化在δr附近变化时引起导引头相位误差为ΔΦ，将式（9）以增量表示，并将式（13）代入，得

式中

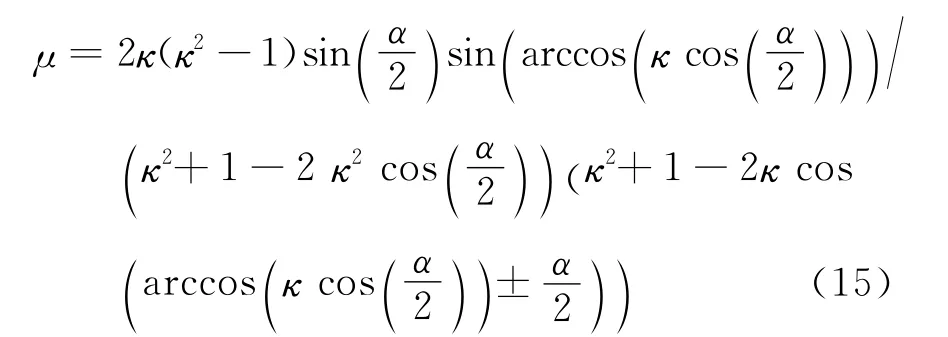
若导引头允许测角误差为Δθ，根据文献［1］中测角误差公式

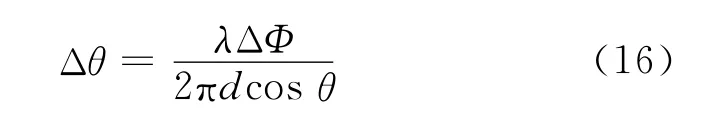
最终得到

因此，当满足

时，PRS跟踪雷达附近，其中μ与δr的“±”相对应。

6）κ＞1时，即ξ＞1／k，干涉仪输出角度θ在θ2附近变化。将式（5）重新写成

相应地，若使得δ满足

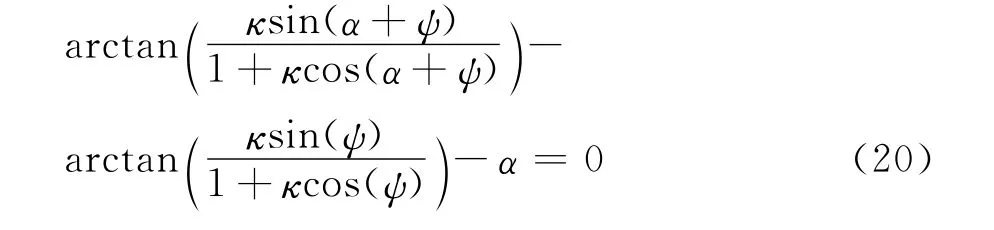
则PRS跟踪诱饵。这时要求

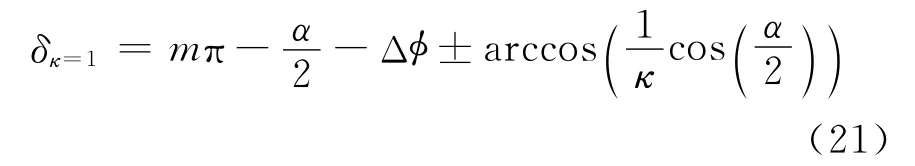
同上所述，当满足

时，PRS跟踪诱饵附近，其中μ满足

3 仿真分析

假设雷达和诱饵的入射方向θ1和θ2不变，取θ1＝0°，θ2＝15°，入射信号波长为λ，相位干涉仪的基线长度d＝λ／2，雷达和诱饵的初始相位差Δφ＝π／12。若δ在［0，2π）之间变化，得到PRS的指向角度随极化因子δ和κ的变化曲线，如图2所示。从图中可以看出，当κ＜1时，PRS的指向角度在雷达附近变化，当κ＝0.7时，PRS在π－α／2－π／12±arccos（κcos（α／2））附近跟踪雷达，且在π－α／2－Δφ处跟踪偏差达到最大；当κ进一步减小到0时，PRS指向0°，跟踪雷达。当κ＞1时，PRS指向诱饵附近，当 κ＝1.4 时，PRS 在 π －α／2－ π／12±arccos（cos（α／2）／κ）附近跟踪诱饵，并在π－α／2－Δφ处跟踪偏差最大；当κ增大到100时，PRS指向15°，跟踪诱饵。当κ＝1时，合成相位差在π－π／12－α和π－π／12处发生π的跳变，PRS的两个指向角度为7.5°和－60.5°.仿真结果与前面的理论分析一致。

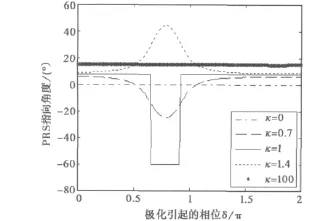
图2 PRS指向角度随极化因子的变化

为了分析雷达极化对单极化干涉仪测角性能的影响，假设诱饵信号为水平极化，导引头接收天线为右旋圆极化，雷达信号的极化在poincare球上变化，其坐标为 （g′1，g′2，g′3）.得到κ和δ 的表达式

当雷达信号极化从poincare球北极至南极变化时，κ的变化区间为若功率比则在球上存在“κ＝1极化环”，当雷达极化落入该圆环时，κ＝1.由式（26）容易得到，该极化环与z轴垂直，见图3，且满足g′3＝k2－1.处于该环以南的极化点使得κ＞1，PRS指向角度在θ2附近变化，越靠近南极，κ越大，PRS指向角度越可能趋近诱饵；当雷达极化对应南极点（右旋圆极化）时，β1＝π，则κ→∞，PRS跟踪诱饵；处于该环以北的极化点使得κ＜1，PRS指向角度在θ1附近变化，越靠近北极，κ越小，PRS指向角度越可能趋近雷达。

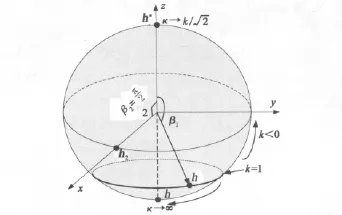
图3 极化影响在poincare球上的描述

考虑到PRS的指向角度还受δ的影响，上述仿真条件不变，PRS测角误差Δθ为3°，图4描绘了当PRS指向角度满足1，2）时，雷达极化在poincare球上对应的分布，为了方便显示，将图4（a）、（b）和（c）的z轴进行了翻转。仿真条件：a）诱饵与雷达的功率比k＝0.7，Δφ＝π／12；b）k＝0.9，Δφ＝π／12；c）k＝1，Δφ＝π／12；d）k＝0.7，Δφ＝0；e）k＝0.7，Δφ＝π／2；f）k＝0.7，Δφ＝π.从图4可以得到以下结论：

1）PRS测角性能与极化有关。若其他仿真条件相同，当雷达极化处于某些区域时，PRS跟踪雷达（蓝色区域）或诱饵（绿色区域），雷达极化的相位分别满足式（18）和式（22）。

2）当雷达极化处于右旋圆极化附近时，κ→∞，PRS指向诱饵。

3）若Δφ给定，随着k的增大，绿色区域有所扩张，蓝色区域减少，当k增大到一定程度，不存在蓝色区域。这说明功率比的增大，虽然有利于保护雷达，但是有可能增加暴露诱饵的风险。

4）若k给定，随着Δφ不同，绿色区域和蓝色区域的分布发生很大的变化。假设雷达信号的极化矢量分布在某特定区域（如左旋圆极化附近），当Δφ＝0时，PRS无法跟踪雷达；但是当Δφ＝π／2时，图4（e）中显示PRS均指向雷达。

若雷达极化为垂直极化，其他仿真条件不变，功率比k＝0.7，Δφ分别为0、π／2和π，则右旋圆极化导引头的指向角度分别为3.1°、－14.3°和5.5°，导引头不能分辨雷达和诱饵。

若导引头接收天线的极化方式可变，诱饵信号极化不变，雷达信号极化为垂直极化，导引头接收天线的极化在poincare球上变化，其坐标为 （g1，g2，g3）。则κ和δ的表达式为

容易得到，“κ＝1极化环”与x轴垂直，满足g1＝－cos（2arctan（1／k））。图5描绘了当PRS指向角度满足时，导引头极化在poincare球上对应的分布，功率比k＝0.7，图5（a）、（b）和（c）中 Δφ分别为0、π／2和π，并将z轴进行了翻转。从图5可以看出，若导引头极化处于图中蓝色区域，PRS跟踪雷达；处于绿色区域，PRS跟踪诱饵，说明变极化导引头通过改变导引头的极化方式，可以使PRS跟踪雷达或诱饵。相对于上述单一右旋圆极化的导引头，变极化导引头对雷达和诱饵的分辨能力有了很大的改善。

4 结 论

从干涉仪测向原理和极化接收理论入手，推导了相干源诱偏下PRS跟踪角度的数学模型，指出PRS跟踪角度不仅受诱饵和雷达信号的幅度比、到达角和初始相位差的影响，还与两信号的极化矢量以及导引头接收天线的极化矢量有关。推导了导引头分别跟踪雷达和诱饵时极化应满足的条件，并采用poincare极化球描述了极化对PRS跟踪角度的影响，进一步指出变极化导引头通过改变导引头的极化方式，可以使PRS跟踪雷达或诱饵，这一结果说明极化信息的利用将有可能改善导引头对雷达和相干源诱饵的分辨。仿真结果验证了结论的正确性。

［1］司锡才.反辐射导弹防御技术导论［M］.哈尔滨：哈尔滨工程大学出版社，1997.

［2］ZHOU Weiguang，LUO Jirun.Performance evaluation of radar and decoy system counteracting anti－radiation missile［J］.IEEE Trans on Aerospace and Electronic Systems，2011，47（3）：2026－2036.

［3］周伟光，王华彬，罗积润.雷达诱饵合成场对反辐射导弹测向系统的影响［J］.电子与信息学报，2009，31（4）：981－984.ZHOU Weiguang，WANG Huabin，LUO Jirun.Effects of the electromagnetic－field－combined profile of radar and decoy on direction－finding system of anti－Radiation Missile［J］.Journal of Electronics ＆Information Technology，2009，31（4）：981－984.（in Chinese）

［4］周伟光，王华彬，罗积润，等.雷达配置诱饵对抗反辐射导弹的仿真［J］.电子与信息学报，2010，32（6）：1370－1376.ZHOU Weiguang，WANG Huabin，LUO Jirun，et al.Simulation of radar equipped with decoys for counteracting anti－radiation missile［J］.Journal of Electronics＆Information Technology，2010，32（6）：1370－1376.（in Chinese）

［5］周伟光，王华彬，罗积润.多辐射源合成场对反辐射导弹的诱偏作用［J］.电子学报，2008，36（6）：1193－1197.ZHOU Weiguang，WANG Huabin，LUO Jirun.Modeling of electromagnetic－field－combined profile of multiple radiation sources as well as its decoying effect on ARM［J］.Acta Electronica Sinica，2008，36（6）：1193－1197.（in Chinese）

［6］曲志昱，司锡才，谢纪岭.相干源诱偏下比相被动雷达导引头测角性能分析［J］.系统工程与电子技术，2008，30（5）：824－827.QU Zhiyu，SI Xicai，XIE Jiling.Analysis of phase－comparison passive－radar－seeker angle measurement with decoy of coherent source［J］.Systems Engineering and Electronics，2008，30（5）：824－827.（in Chinese）

［7］李兴华，顾尔顺.ARM干涉仪导引头对chirp信号辐射源测角误差研究［J］.系统工程与电子技术，2008，30（12）：2349－2351.LI Xinghua，GU Ershun.Study on error in chirp radiator direction－finding using ARM interferometer seeker［J］.Systems Engineering and Electronics，2008，30（12）：2349－2351.（in Chinese）

［8］庄钊文，肖顺平，王雪松.雷达极化信息处理及其应用［M］.北京：国防工业出版社，1999.

［9］罗 佳，王雪松.天线空域极化特性的表征及分析［J］.电波科学学报，2008，3（4）：620－629.LUO Jia，WANG Xuesong.Description and analysis of spatial polarization characteristics of antenna［J］.Chinese Journal of Radar Science，2008，23（4）：620－629.（in Chinese）

［10］李金梁，戴幻尧，王雪松，等.抛物面反射天线的空域瞬态极化特性研究［J］.电波科学学报，2009，24（1）：126－131.LI Jinliang，DAI Huanyao，WANG Xuesong，et al.Virtual polarization receiver based on the spatial polarization characteristics of antenna［J］.Chinese Journal of Radar Science，2009，24（1）：126－131.（in Chinese）

［11］戴幻尧，李永祯，王雪松，等.相控阵天线空域极化特性的高频仿真分析［J］.电波科学学报，2011，26（2）：316－322.DAI Huanyao，LI Yongzhen，WANG Xuesong，et al.High frequency simulation analyses of spatial polarization characteristic of phased array antenna［J］.Chinese Journal of Radar Science，2011，26（2）：316－322.（in Chinese）

［12］刘 勇，戴幻尧，王雪松，等.空域虚拟极化滤波原理及实验结果［J］.电波科学学报，2011，26（2）：272－278.LIU Yong，DAI Huanyao，WANG Xuesong，et al.Principle and experimental results of spatial virtual polarization filtering algorithm［J］.Chinese Journal of Radar Science，2011，6（2）：272－278.（in Chinese）

［13］司锡才，赵建文.宽频带反辐射导弹导引头技术基础［M］.哈尔滨：哈尔滨工程大学出版社，1996.