线性调频步进信号雷达目标运动参数估计方法

何 劲 张 群 罗 迎 朱小鹏 邓冬虎

（空军工程大学电讯工程学院，陕西 西安710077）

引 言

逆合成孔径雷达（ISAR）主要通过发射线性调频信号来实现对运动目标的高分辨成像［1－2］，但线性调频信号的带宽制约了雷达成像分辨率的提高，因此，人们开展了线性调频步进信号雷达的研究。线性调频步进信号雷达通过序贯发射多个频率步进的线性调频信号来合成高分辨的目标距离像，可以在不增加系统瞬时带宽的情况下用数字信号处理的方法提高成像分辨率并解决普通步进频率信号高数据率与雷达作用距离之间的矛盾，所以在近年来被广泛应用于雷达成像领域［3－4］。但线性调频信号属于多普勒敏感信号，这种信号体制的雷达容易受到目标运动的影响，发生目标运动速度与距离耦合的问题，所以利用线性调频步进信号雷达对运动目标进行成像时首先需要解决运动参数估计及补偿的问题［5］。

线性调频步进信号属于频率步进信号的一种，因此，频率步进信号雷达的目标运动参数估计方法大多可以用于线性调频步进信号雷达。典型的目标运动参数估计方法主要包括最小脉组误差法、最小熵准则法、最大似然估计法、时域互相关法以及频域互相关法等［6－12］，但这些方法有的运算量较大，有的抗噪性较差，有的较为耗费系统资源［13］。本文在对线性调频步进信号雷达回波进行分析的基础上，提出了一种基于维格纳分布（WVD）、Radon变换和二值数学形态学的线性调频步进信号雷达目标运动参数估计方法。首先根据回波信号具有的线性调频特性，利用WVD 将其变换成直线，通过Radon变换估计直线斜率以完成对目标运动参数的估计。其次，针对部分目标散射点较多的情况，引入二值数学形态学方法提高运动参数估计精度；针对目标存在的变速运动情况，通过最小二乘算法拟合出目标在不同时刻的运动速度变化曲线，完成对变速目标的径向速度补偿。仿真实验验证了本文算法具有较高的效率和较好的抗噪性能。

1.线性调频步进信号雷达回波分析

线性调频步进信号波形的频率随时间变化关系如图1所示，其中每一个子脉冲都是一个线性调频信号，每一簇脉冲串中的第i个子脉冲信号的表达式为（设信号起始时间为－Tp／2）

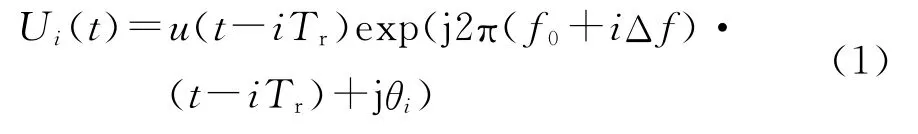
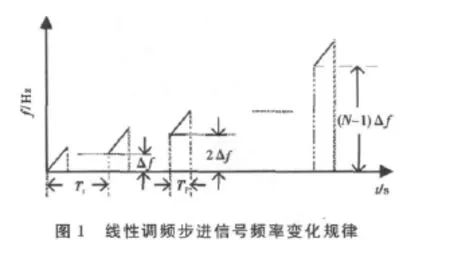
式中：0≤i≤N－1，N为每一簇子脉冲串中的步进频率数；u（t）＝rect（t／Tp）·exp（jπμt2）为线性调频子脉冲，t为快时间（即脉冲串内的时间），μ为子脉冲调频斜率，Tp为子脉冲宽度，Tr为子脉冲重复周期；f0＋iΔf为第i个调频步进子脉冲的载频；θi为第i个子脉冲初相。

假设点目标到雷达的初始距离为R，并以速度vr远离雷达运动，c为电磁波速度，则t时刻目标与雷达的距离R（t）≈R＋vriTr，第i个子脉冲的回波信号可写为

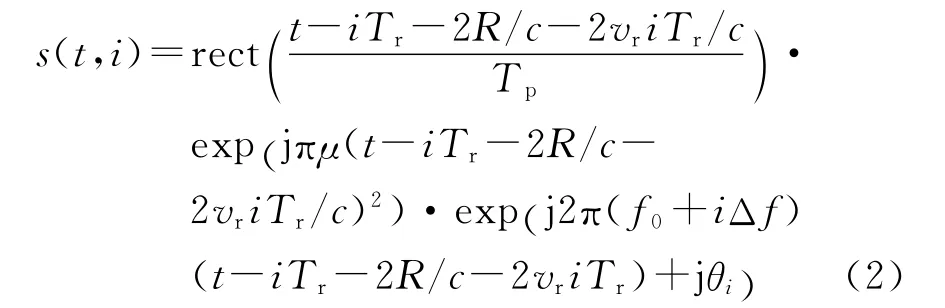
对目标的回波信号做“dechirp”处理，即让参考信号与回波信号进行共轭相乘可以获得目标的粗分辨距离像。在此基础上再对各次子脉冲做二次脉压就可以获得目标的精分辨距离像。假设参考信号可以表示为

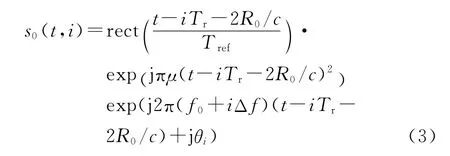
式中：R0为参考点到雷达距离；Tref是参考信号脉宽，比Tp略大。“dechirp”处理后可得

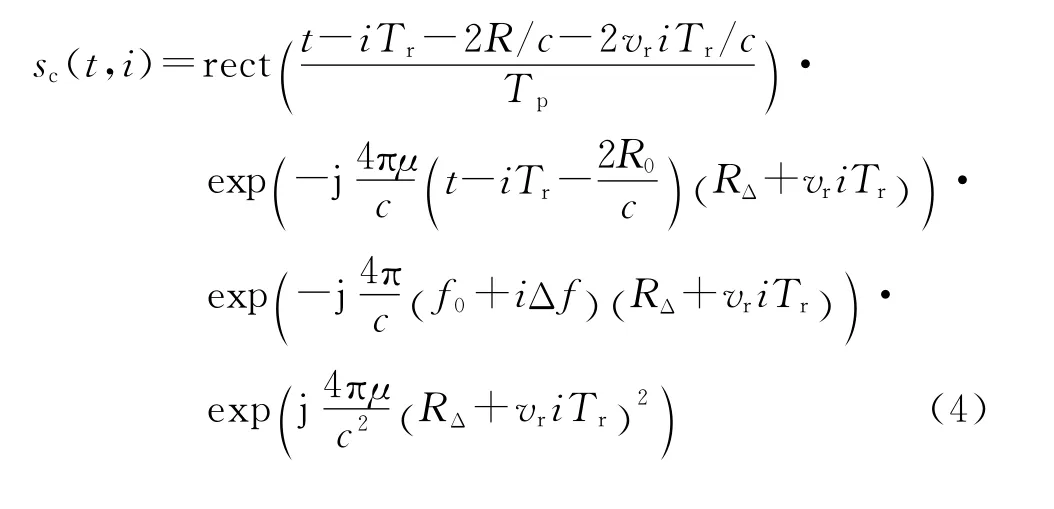
式中，RΔ＝R－R0.以参考点的时间为基准，即令t′＝t－iTr－2R0／c，对式（4）作关于t′的傅里叶变换，并去除剩余视频相位项和包络斜置项后，可以得到［14］

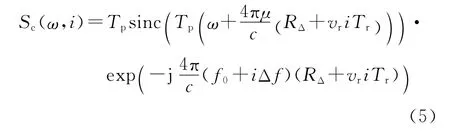
从式（5）可以看出，如果目标的径向速度vr＝0，是一个峰值在ω＝－4πμRΔ／c处的sinc函数，此即点目标的粗分辨一维距离像。通常目标的径向长度会小于不模糊距离区间长度，因此，在得到粗分辨距离像的基础上，对该距离单元进行采样就能获得目标上各散射点的全部信息。令ω＝－4πμRΔ／c，对各次粗分辨距离像做关于i的傅里叶变换，可以得到

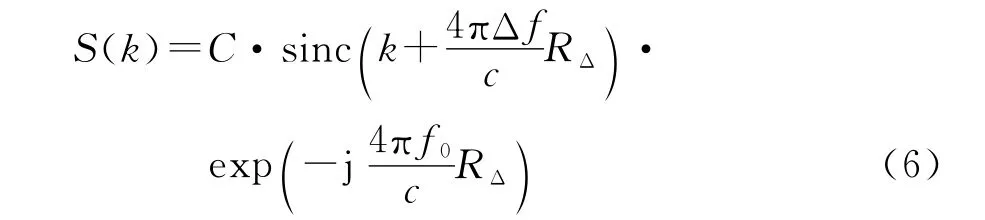
实际情况下目标的径向速度会导致一维距离像包络峰值的偏移、展宽和能量的发散并影响二维成像结果。因此，需要在成像之前进行补偿。当目标的径向速度vr≠0时，对式（5）的相位关于i求导数，可以推出目标精分辨距离像将在式（7）所给出的k处出现峰值。

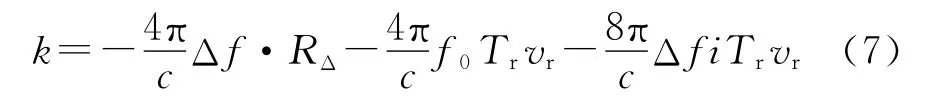
式（7）中共包含三个相位项，第一项为距离项，它与式（6）中峰值的位置相同，反映的是目标散射点的真实位置；第二项为由目标径向速度引起的距离像走动；第三项是由速度vr与子脉冲个数i的耦合引起的，它会导致精分辨距离像峰值的展宽，目标运动速度越快，该项的影响越大［15］。

精分辨像由粗分辨像作N点离散傅里叶变换得到，其频率范围为 ［－π，π］，这一频率范围决定了精分辨像的成像距离范围，如果k的取值超出［－π，π］后，散射点的峰值位置将发生卷绕，即出现距离模糊。要避免距离模糊必须满足即

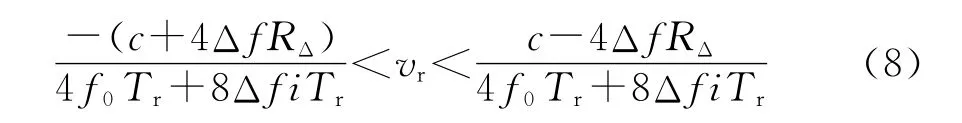
假设散射点到参考点的距离RΔ＝5m，雷达信号的载频f0＝20GHz，频率步进值Δf＝5MHz，子脉冲重复周期Tr＝100μs，子脉冲i＝60，则避免距离模糊的径向速度vr的范围为（－32.679 7m／s，16.339 9m／s）.普通的运动目标（如飞机等）的径向速度肯定将超过这一范围，因此，距离模糊是不可避免的，需要进行补偿。

3.基于时频分析的目标运动参数估计和补偿

2.1 匀速运动目标速度估计

设式（5）的相位为Φ（i），将其展开可得

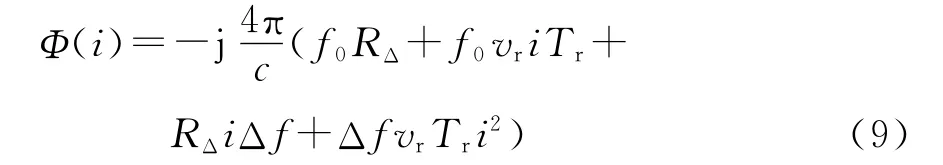
可以看出，Φ（i）中包含了关于子脉冲数i的一次项和二次项，可以近似为一个关于i的线性调频信号。由于线性调频信号的WVD体现为直线特征，直线的斜率就是信号的调频斜率，因此，考虑首先获得信号Sc（ω，i）的WVD分布，并在此基础上通过Radon变换检测得到直线的截距和斜率。由于直线斜率b＝－ΔfvrTr／c，Δf和Tr为已知的雷达信号参数，所以可以由此推出目标的径向速度vr.令A＝Tpsinc（Tp（ω＋4πμ（RΔ＋vriTr））／c），fc＝－2（f0vrTr＋RΔΔf）／c，K＝ －4ΔfvrTr／c，g＝－2f0RΔ／c，将Sc（ω，i）重新写为

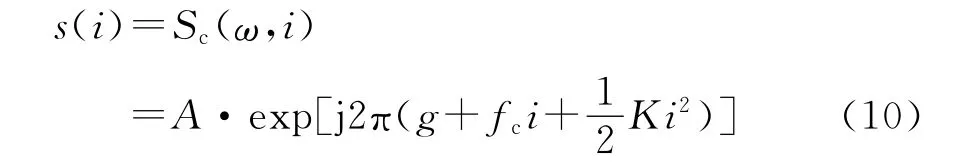
s（i）的WVD 可以表示为

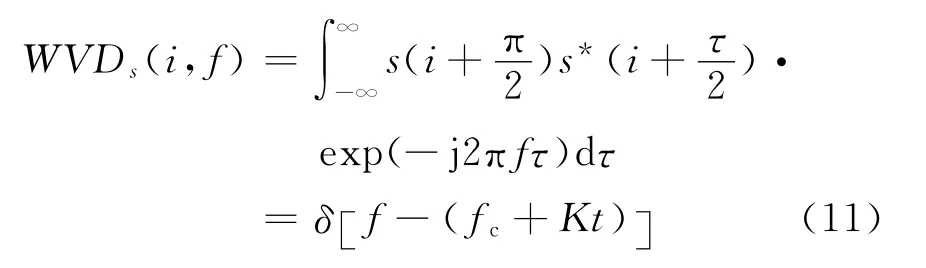
从式（11）可以看出，Sc（ω，i）的WVD 在时频面呈现出沿直线广义分布的冲激直线谱，信号的起始频率和调频斜率分别对应直线的截距和斜率，只要检测出直线的斜率就可以推出运动目标的径向速度。但由于目标包含的散射点数量很多，回波信号并不是一个简单的单分量线性调频信号，而是由多个不同散射点的回波组成的一组具有相同调频斜率、不同起始频率的多分量线性调频信号，不同分量之间的WVD会存在交叉项，因此，通过重排平滑处理来解决这一问题，即对Sc（ω，i）进行重排维格纳分布（RSPWVD）。

对Sc（ω，i）进行RSPWVD 包括两个步骤，首先用二维低通滤波器Φ（t′，f′）对Sc（ω，i）的 WVD 进行平滑处理，其次通过改变平均点归属，重新分配平均点到时频分布能量的引力重心来避免信号能量的扩散。假设引力重心对应的坐标和可以表示为［16］

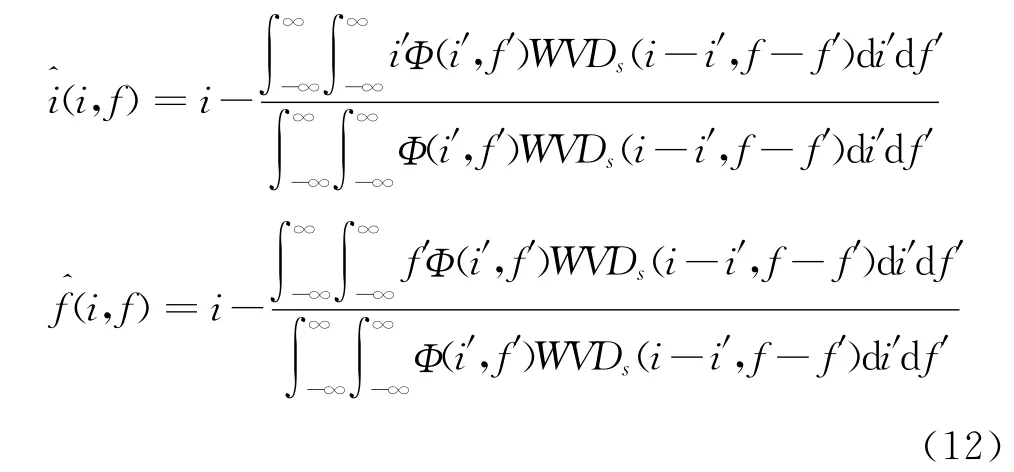
则Sc（ω，i）的RSPWVD 可表示为［16］

得到Sc（ω，i）的RSPWVD 后，通过 Radon变换求解直线的斜率。假设平面（x，y）上存在任意二维函数f（x，y），当x＝ucosθ－vsinθ，y＝usinθ＋vcosθ时，它的Radon变换可以表示为

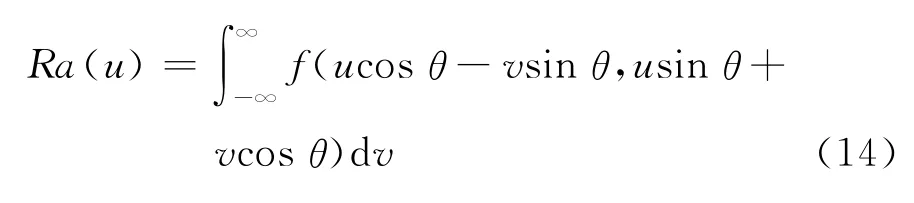
Ra（u）是u和θ的二维函数。令K＝－cosθ，fc＝u／sinθ，在 Radon平面上，参数（K，fc）处将会呈现尖峰，而其他地方，积分能量会减小。因此，通过Radon变换可以检测到RSPs（i′，f′）的斜率，即Sc（ω，i）的调频斜率。利用估计的调频斜率可以得到运动目标径向速度的估计值＾vr，并以此为依据构造补偿因子H 对Sc（ω，i）进行补偿。对补偿后的Sc（ω，i）作关于i的快速傅里叶变换，即可以得到较为精确的目标精分辨距离像。

当雷达分辨率较高，回波信号中包含的目标散射点太多时，利用RSPWVD对回波信号进行处理可能仍然会遇到问题，由于所有散射点的回波具有相同的斜率，我们考虑进一步利用图像处理方法来获得更准确的目标速度估计，主要步骤包括：

1）设置合适阈值，将回波信号的RSPWVD转换为二值图像；

2）利用膨胀处理将图像平滑化。根据二值数学形态学，设f为图像中的目标区域，用结构元素a对f进行膨胀记为f⊕a，定义

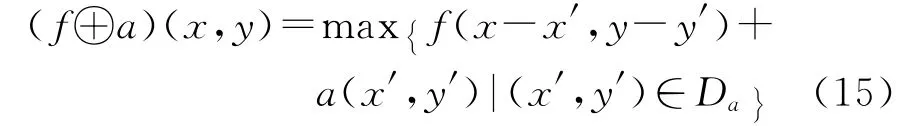
式中：Da是a的定义域；f（x，y）在f的定义域外假设为－∞.可以认为结构元素关于其原点旋转并在图像中的所有位置平移，在每个平移位置，将结构元素的值与图像像素值相加并计算出最大值。

3）对膨胀处理后的图像进行边缘检测会得到两条斜率相同的直线，利用Radon变换进行检测可以得到两个具有相同θ的峰值，从而推出直线斜率及目标的径向速度。

2.2 变速运动目标速度估计

由于成像时间通常较短，当目标平稳飞行时，可以认为目标的径向速度在整个成像过程中是近似不变的，只需要对一簇回波进行时频分析就能有效估计出目标径向速度。但如果目标在做机动飞行，其径向速度将发生瞬时变化，所以，本文对变速目标进行速度估计时，在对多簇不同时刻回波脉冲进行时频分析的基础上，采用最小二乘法拟合出目标在整个成像过程中的速度变化曲线，以实现更加精确的径向速度补偿。

由于每一个脉冲簇的持续时间极短，通常只有数毫秒，因此可以认为目标在每一个脉冲簇的时间内是近似做匀速运动，即可以利用上述方法估计出目标在各脉冲簇内的速度，在此基础上进一步用最小二乘算法拟合出目标在整个成像时间内的速度变化曲线。假设在成像时间Tc内利用n簇回波信号估计出的n个速度值构成一系列的散点f（xi，yi），i＝1，2，…n，其中x轴表示时间，y轴表示速度。则可以通过寻找使误差ei＝f（xi）－yi平方和最小的曲线f（x）来实现速度曲线的拟合，即求解

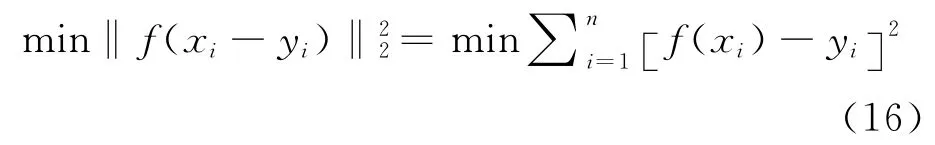
通过曲线拟合，成像过程内各个时间点的目标径向速度估计值都可以得到，因此，可以在此基础上完成径向速度的补偿。

3.仿真分析

3.1 匀速运动目标运动参数估计及成像

实验1：速度估计实验

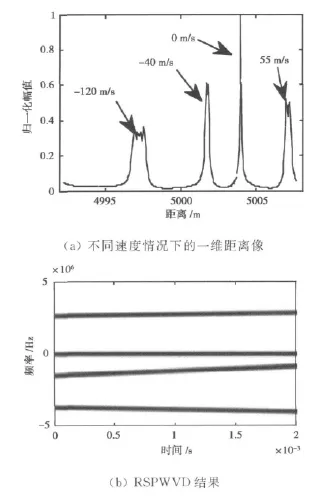
首先对基于时频分析的目标运动参数估计方法进行验证。假设雷达发射的线性调频步进信号的起始载频为30GHz，信号脉宽为0.976 562 5μs，子脉冲间隔为7.812 5μs，每一簇脉冲共包含256个子脉冲，子脉冲的带宽为3.906 25MHz，子脉冲之间的单位步进频率为3.906 25MHz，合成带宽为1 GHz，脉冲重复频率为500Hz，即在1s内发射了500簇脉冲串。假设存在四个点目标，与雷达的初始距离为5 004m，瞬时的径向速度分别为0m／s，55m／s，－40m／s和－120m／s.图2（a）为四个点目标的一维距离像，可以看出，当目标径向速度为零时，峰值点明显；当目标存在径向速度时，一维距离像的幅值会降低，而且会出现不同程度的展宽、平移，甚至卷绕，速度越大，展宽和平移越明显。因此，如果在补偿径向速度前进行回波信号重构，是无法准确找到散射点的真实位置的。图2（b）为对“dechirp”后的回波信号进行重排WVD 变换的结果，当径向速度为0时，直线的斜率为0，当径向速度不为0时，直线的斜率受到速度的影响各不相同。图2（c）是对直线进行Radon变换后的结果，一共包含四个峰值点，分别与图2（b）中四条直线相对应，不同斜率的直线在Radon变换域中的峰值位置各不相同。从中可以计算出直线的斜率并推导出四个点目标的速度分别为0m／s，55.02m／s，－40.01m／s和－120.03m／s，速度估计误差均不超过0.01%，这说明了本文速度估计算法的有效性。

实验2：成像实验

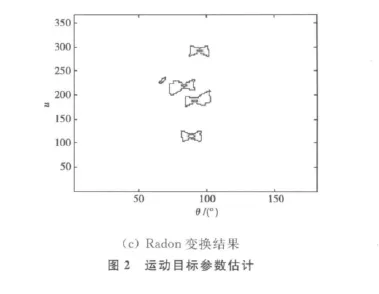
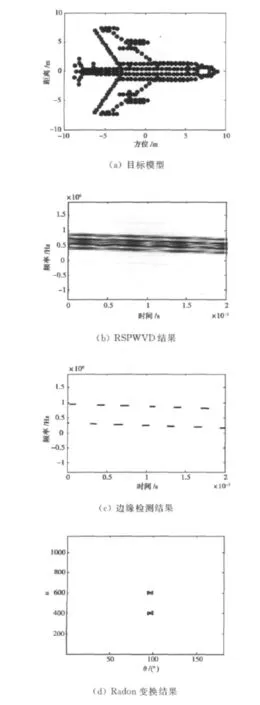
假设雷达发射信号的参数与实验1相同，对图3（a）所示的飞机模型进行成像实验，飞机与雷达的初始距离为20km，飞行径向速度均为120m／s，以45°的俯仰角朝斜上方飞行，每一簇脉冲串的持续时间为2ms，成像时间约为3.93s，相对于雷达的转角为0.033rad，对应的方位分辨率为0.15m，仿真过程中假设目标与雷达的距离能够较为准确的测量，利用基于参考点的补偿方法完成平动补偿，测速结果如图3所示。

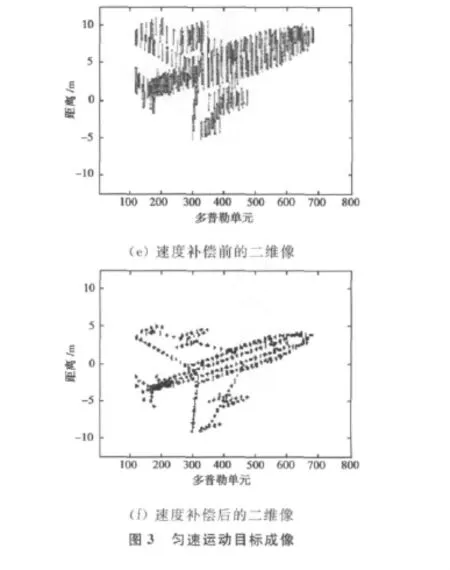
对第20簇脉冲的回波信号进行“dechirp”处理和RSPWVD后，得到的结果如图3（b）所示，为一组具有相同斜率的直线，由于散射点较多，回波信号的RSPWVD仍然受到了交叉项的影响。按照2.1节所述的步骤对图3（b）进行处理，得到的边缘检测结果如图3（c）所示，是两条具有相同斜率的直线，对直线进行Radon变换，得到的结果如图3（d）所示，两条直线在Radon域具有相同的θ值，通过计算可以估计出目标的径向速度为120.67m／s，误差率为0.46%，这说明了本文速度估计算法的有效性。图3（e）和图3（f）分别为补偿前后的二维成像结果，补偿后图像的质量得到了较为明显的改善。

3.2 变速运动目标运动参数估计及成像

假设雷达发射信号参数不变，飞机在整个成像时间内做匀加速运动，径向速度初始值为100m／s，加速度为10m／s2，以45°的俯仰角朝斜上方飞行。假设方位向分辨率与距离向分辨率相同，均为0.15m，合成孔径长度为666.67m，成像时间约为4.115s.由于每一簇脉冲串的持续时间为2ms，所以在成像时间内共可以发射2 057簇脉冲串，即可以完成2 057次测速。目标在整个成像时间内的速度变化如图4（a）所示，利用本文算法对所有脉冲簇进行处理后可以得到2 057个速度值，对这些速度值进行最小二乘拟合，得到的结果如图4（b）所示，拟合得到的结果与真实值基本相符。图4（c）为利用估计出的速度完成径向运动补偿后得到的目标二维像，成像结果基本克服了目标径向速度的影响。

3.3 噪声对速度估计的影响分析

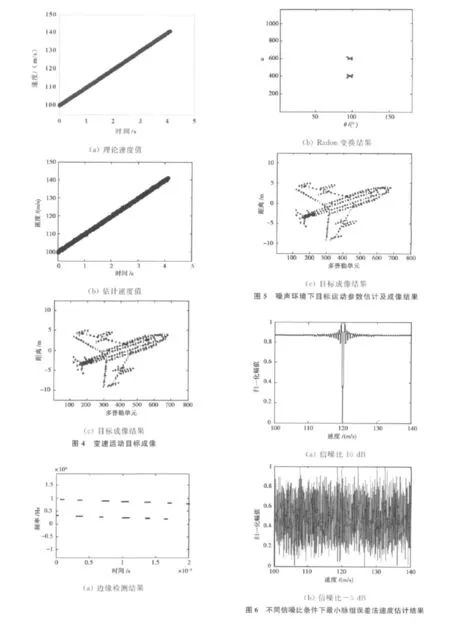
为了进一步证明本文算法的性能，在仿真中对含噪的回波信号进行处理，并与经典的最小脉组误差法进行比较。假设雷达发射信号的参数不变，飞机与雷达的初始距离为20km，飞行径向速度均为120m／s，以45°的俯仰角朝斜上方飞行，当接收端信噪比为－5dB时，利用时频分析和Radon变换的回波信号进行分析的结果如图5（a）、（b）所示。可以看出，由于Radon变换具有较强的鲁棒性，在一定噪声的影响下，仍然能较为准确地测到目标的运动速度。最终得到的速度估计值为120.87m／s.利用估计的速度进行径向运动补偿，得到的二维成像结果如图5（c）所示，基本克服了目标径向速度的影响。利用最小脉组误差法对目标速度进行估计的结果如图6所示，图6（a）和图6（b）分别是接收端信噪比为10dB和－5dB时的结果，当接收端信噪比为10dB时，速度估计误差为0.5m／s，当接收端信噪比为－5dB时，估计失效。因此，本文算法的抗噪性能要强于经典的最小脉组误差法。除此之外，利用最小脉组误差法进行速度估计需要具备一定的先验知识以确定速度搜索的范围，如果搜索范围过大则会影响速度估计的效率，而本文算法则不需要先验知识。

4.结 论

针对目标运动过程中径向速度对线性调频步进信号成像结果带来的展宽和徙动的影响，本文提出了一种基于时频分析的目标运动参数估计方法，利用目标回波信号与子脉冲序列之间的线性调频关系，通过WVD和Radon变换对目标的径向速度进行估计，得到了目标在不同时刻的运动参数，并结合二值数学形态学、图像边缘检测和最小二乘拟合方法实现了对多散射点目标径向速度的估计。实验结果表明：利用本文方法估计的速度进行径向运动补偿后，可以得到较好的目标二维像。

［1］陈文驰，刘 飞.一种低信噪比下的ISAR成像实现方法［J］.电波科学学报，2010，25（3）：585－589.CHEN Wenchi，LIU Fei.An implementation method of ISAR imaging at the low SNR level［J］.Chinese Journal of Radio Science，2010，25（3）：585－589.（in Chinese）

［2］崔艳鹏，胡建伟，杨绍全.一种基于SVM的超分辨成像算法研究［J］.电波科学学报，2009，24（3）：566－570.CUI Yanpeng，HU Jianwei，YANG Shaoquan.A super－resolution algorithm for radar imaging based on SVM［J］.Chinese Journal of Radio Science，2009，24（3）：566－570.（in Chinese）

［3］王虹现，全英汇，邢孟道，等.步进线性调频信号舰船ISAR成像的实时信号处理［J］.数据采集与处理，2011，25（3）：401－406.WANG Hongxian，QUAN Yinghui，XING Mengdao，et al.Real－time data process for ISAR imaging of ship targets using stepped－chirp signal［J］.Journal of Data Acquisition and Processing，2011，25（3）：401－406.（in Chinese）

［4］袁昊天，文树梁，程 臻.调频步进信号高速运动目标径向速度精确测量技术研究［J］.电子学报，2009，37（3）：649－654.YUAN Haotian，WEN Shuliang，CHENG Zhen.Accurate velocity measurement of high speed moving target about stepped－frequency chirp signal［J］.Acta Electronica Sinica，2009，37（3）：649－654.（in Chinese）

［5］李 眈，龙 腾.步进频率雷达目标去冗余算法［J］.电子学报，2000，28（6）：60－64.LI Dan；LONG Teng.Targets redundance removed algorithms of step frequency radar［J］.Acta Electronica Sinica，2000，28（6）：60－64.（in Chinese）

［6］ZHANG Q，YEO T S，DU G.ISAR Imaging in strong ground clutter by using a new stepped－frequency signal mode.IEEE Transactions on GRS，2002，49（3）：2759－2755.

［7］CHEN H Y.A new approach for synthesizing the range profile of moving targets via stepped－frequency waveforms.IEEE GRS Letters，2006，3（3）：406－409.

［8］王鹏宇，宋 千，金 添.步进频率SAR快时间多普勒效应补偿新方法［J］.电子与信息学报，2009，31（9）：2053－2058.WANG Pengyu，SONG Qian，JIN Tian.A new fasttime Doppler effect compensation method applied to step frequency SAR system［J］.Journal of Electronics Information Technology，2009，31（9）：2053－2058.（in Chinese）

［9］原浩娟，高梅国，牟建超.基于多普勒通道对齐的多帧步进频信号速度补偿方法［J］.电子与信息学报，2009，31（7）：1659－1663.YUAN Haojuan，GAO Meiguo，MU Jianchao.Multiframe stepped－frequency signal processing based on Doppler bin alignment［J］.Journal of Electronics Information Technology，2009，31（7）：1659－1663.（in Chinese）

［10］HE S，ZHU Y F，ZHAO H Z，et al.Analysis of rotating structures for stepped frequency radar［C］∥IEEE International Conference on Radar.Adelaide，Australia，2008：386－390.

［11］吴晓芳，刘 阳，王雪松，等.基于频率步进雷达时间－距离像的宽带微动特征提取［J］.电子学报，2009，37（7）：1416－1421.WU Xiaofang，LIU Yang，WANG Xuesong，et al.Feature extraction of wide－band micro motions based on stepped－frequency radar time－range profiles［J］.Acta Electronica Sinica，2009，37（7）：1416－1421.（in Chinese）

［12］SCHIMPF H，WAHLEN A，ESSEN H.High range resolution by means of synthetic bandwidth generated by frequency－stepped chirps［J］.Electron Letter，2003，39（18）：1346－1348.

［13］曹宇飞，屈晓光，黄培康.双载频步进频率雷达精确速度测量方法［J］.电子与信息学报，2009，31（5）：1113－1116.CAO Yufei，QU Xiaoguang，HUANG Peikang.Precise velocity measurement approach in dual－carrier－frequency stepped－frequency radar［J］.Journal of Electronics Information Technology，2009，31（5）：1113－1116.（in Chinese）

［14］LUO Y，ZHANG Q，QIU C W，et al.Micro－Doppler effect analysis and feature extraction in ISAR imaging with stepped－frequency chirp signals，IEEE Transactions on GRS，2010，48（4）：2087－2098.

［15］李亚超，梁 毅，邢孟道，等.基于线性调频步进ISAR参数估计和成像算法研究［J］.电子学报，2008，36（2）：2464－2472.LI Yachao，LIANG Yi，XING Mengdao，et al.Estimation of motion parameters and research of imaging algorithm based on LMFS ISAR［J］.Acta Electronica Sinica，2008，36（2）：2464－2472.（in Chinese）

［16］AUGER F，FLANDRIN P.Improving the readability of time－frequency and time－scale representations by the reassignment method［J］.IEEE Trans on SP，1995，43（5）：1068－1089.