基于Rogowski谐振原理及小波能谱的暂态保护

牟龙华，张 鑫，朱吉然，2

（1.同济大学 电气工程系，上海201804；2.湖南省电力公司科学研究院，湖南 长沙410007）

配电网络的继电保护大多采用基于工频量的保护原理，存在处理时间长或对通信要求高等问题，对供电可靠性的影响较大.对于传统的三段式过流保护而言，配电网结构复杂，采用工频保护不仅参数整定困难，并且速度慢、快速保护范围有限，难以满足保护的要求.

暂态行波保护原理为配电网保护提供了新的解决思路.利用故障产生的暂态行波信号在线路区内外差异的特征可以构成具有全线速动性的保护方案.此类保护成立条件在于故障暂态分量在边界两侧存在明显差异，并且该差异具有规律性可被提取作为保护判据［1］.在高压输电线路中，由于各段线路边界处串联有一定频带的阻波器，加之母线杂散电容的存在，将相应高频暂态成分限制在故障区段内，从而形成区段保护判据.

本文提出一种基于Rogowski线圈谐振原理和小波能谱的配电网暂态保护新方案，即在线路边界接入基于Rogowski线圈的谐振装置，其二次负载端接入谐振电容和负阻抗变换器，从而改变线路边界谐振处暂态信号传输特性，以此区分区内外故障，实现配电网的全线速动保护.

1 基于Rogowski谐振原理的暂态保护

基于Rogowski线圈谐振原理保护方案的实现思路如图1所示.图中：S1，S2分别为系统的两个电源；C1，C2和C3分别为母线N，M和P的对地等效电容.在配电网络各线路边界处接入基于Rogowski线圈的谐振装置（罗氏谐振装置），该装置通过改变线路边界处暂态行波的传输特性为区分区内外暂态信号提供边界条件.

图1 基于罗氏谐振装置的暂态保护原理图Fig.1 Transient traveling wave protection based on Rogowski resonance theory

1.1 Rogowski线圈基本原理

Rogowski线圈即在一个截面均匀的非磁性材料的骨架上均匀地绕上测量导线，由于其不存在磁饱和动热稳定性问题，具有频带宽、自身上升时间小等特点，适于测量快速变化的电流，具有很好的频率特性［2］.Rogowski线圈的等效电路如图2所示.图中：I1，I2分别为一次载流线路和Rogowski线圈电流；U1，U2分别为一次侧电压和Rogowski线圈输出电压；R1，L1是一次线路等效电阻和电感；R2，L2为Rogowski线圈内部电阻和自感；Cc为线圈内部分布电容（由于该电容很小，在计算时忽略不计）；Zload为线圈负载；M为线圈与被测载流导体之间的互感，取决于线圈的结构参数及位置；ω为角频率；j为虚数.

图2 Rogowski线圈等效电路图Fig.2 Equivalent circuit of Rogowski coil

根据图2电路可得方程：

求解式（1）和（2）联立的方程组可得：

由式（3）可以得到Rogowski线圈等效到一次侧的等效阻抗Z1，表达式如下：

R1、L1值很小.由式（5）可以看出，为了提高Z1值，可以合理选择负载阻抗Zload，使得jωL2和Zload在一定频率下处于谐振状态；但互感M为μH级，谐振频率处Z1的值将主要取决于R2.为保证谐振频率处Z1具有更大突变值，引入负阻抗变换器将R2抵消，此时Zload电路如图3所示.R3，R4分别为两个运算放大器反馈电阻；RL为负载电阻；I3为输入电流；U2，U3分别为电容C2两侧的电压.

图3 Rogowski线圈负载等效电路图Fig.3 Equivalent circuit of Rogowski coil load

根据文献［3］可知当R3＝R4时，Z3＝U3／I3＝－RL.选取RL＝R2，即可将罗氏线圈内阻R2抵消，使得L2和C2处于谐振状态.选择具有较大互感M的Rogowski线圈，则在该谐振频率处一次侧等效阻抗Z1将发生突变，从而改变线路边界折反射系数的频谱特性，创造线路边界条件.

罗氏线圈通常是均匀密绕在一个塑料棒构成的环形骨架上，骨架的横截面一般为圆形或矩形.考虑到6～10kV及以下电压等级配电线路供电电缆的常用外径，参照文献［4］中的罗氏线圈优化设计准则，为达到较好的边界效果，本文中罗氏谐振装置采用骨架截面为圆形的线圈，骨架截面中心到骨架中心的距离A＝100mm，骨架截面半径B＝20mm，匝数N＝3 000，用Φ0.6mm的铜线绕制，空气导磁系数为μ0，根据公式及电桥法可得到线圈内阻R2＝37.28Ω，自感L2＝27.78mH，互感M＝9.26μH.

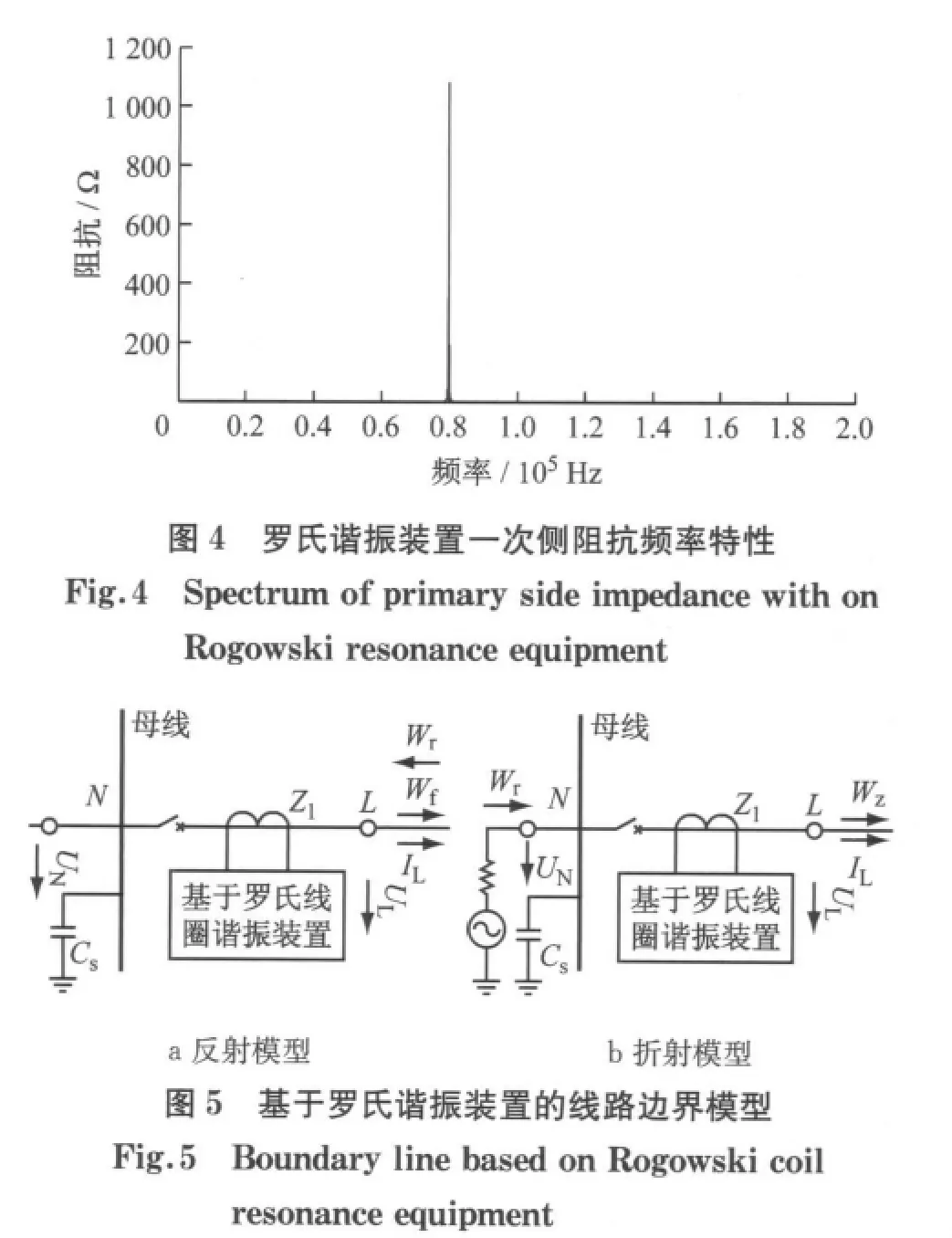
由图4可看出，一次侧等效阻抗Z1在谐振频率附近呈现高阻抗（约1 100Ω，而在其他频带阻抗则很小，不会对工频电流和配网的运行产生影响.

1.2 基于罗氏谐振原理的线路边界频率特性

当线路发生故障时，故障点处暂态行波特征主要由线路边界折反射系数的频谱特征所决定.影响线路边界折反射系数的因素包括母线对地等效电容、线路故障时接地电阻等.

以下分析接入罗氏谐振装置的线路边界对暂态行波的影响，即线路边界折反射系数的频率特性.线路边界反射模型如图5a所示.图中：UN为电压额定电压；IL，UL分别为故障点L处的行波电流和行波电压；CS为母线对地等效电容；Z1为罗氏谐振装置等效到一次侧阻抗；ZC为线路波阻抗；前行波Wr、反行波Wf及电压、电流参考方向如图所示.折射模型如图5b所示，假设故障处附加电源Us经故障过渡电阻Rg连接到母线N，电源产生入射波Wr＝Us，Wr经过线路边界到故障点L产生折射波Wz.

根据行波理论以及基尔霍夫电压（KVL）定理可以求得线路边界反射系数Kf（s）和折射系数Kz（s）［5－6］为

式中：s为拉氏变换复数因子.

式中：Rg为故障点过渡电阻；Z′t为阻波器等值阻抗.

按照1.1节选取罗氏谐振装置参数，其他参数：Zc＝300Ω、CS＝0.01uF和Rg＝10Ω，根据式（6）和式（7）作出线路边界频率特性如图6所示.

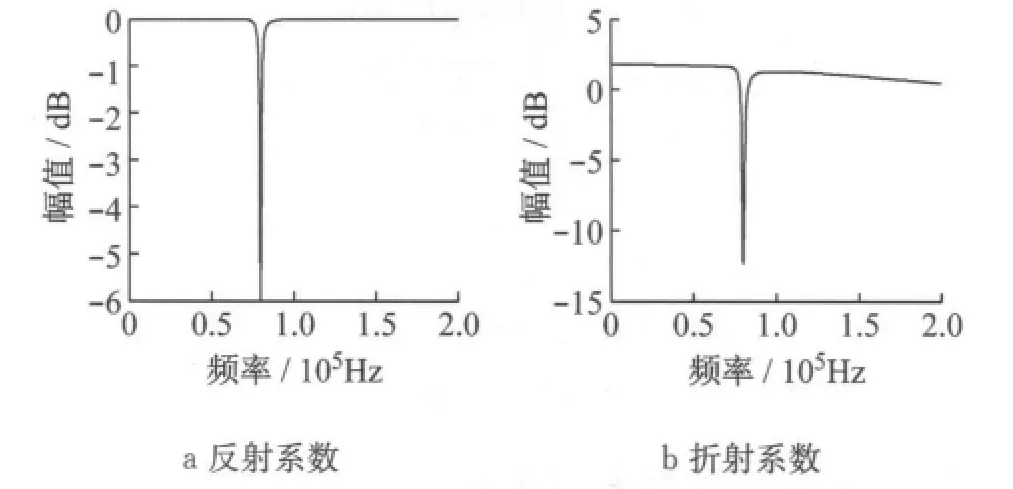
图6 基于罗氏谐振装置线路边界频率特性Fig.6 Spectrum of boundary line based on Rogowski resonance equipment

由图6可看出：罗氏谐振装置对于线路边界折、反射系数的影响效果显著，使得反射系数在谐振频带内有较小的衰减（约6dB），而折射系数在该频带内有较大的衰减（约15dB），从而导致区内外暂态行波频谱特性的差异.

2 基于模极大值和能谱的暂态保护

单端测量的故障暂态行波在线路上的来回折反射使得暂态分量的频谱随时间变化［7］，因此不可使用Fourier变换来分析故障暂态分量.而小波变换具有良好的频域和时域特性，为分析故障暂态信号在某时间段内具体频带的频谱提供了很好的途径.

2.1 小波基的选择

暂态保护要求分析故障暂态量特定时段特定频段内的频谱特性，这就要求小波具有良好的时频定位效果.并且为了保证没有冗余的信号表示和完美的信号重构以及计算的实效性和快速性，要求小波为紧支撑的正交小波［8］.同时由于需要提取暂态信号不同频段内的信号，要求小波分频严格，能量集中［9］.因此，本文选择具有紧支撑的正交小波Db4小波进行故障暂态信号的分析和能谱的提取.

2.2 基于小波模极大值的故障启动判据

故障暂态信号突变点必定是奇异的，可以用奇异性指数Lipschitzα来描述信号的奇异性，从而检测或识别暂态信号的突变点［10－12］.本文利用小波变换模极大值在多尺度上的综合表现来判断信号突变点，作为暂态保护的故障启动判据.

2.3 基于小波多分辨率的能谱提取

假设对经过归一化频率的暂态信号x（n）作多尺度小波变化，在第j（j＝1，2，3，…，J）尺度下对应的高频分量为Dj，低频分量为Aj.信号分解后对应归一化频率范围如图7所示.图中，G（ω）为高通滤波器，H（ω）为低通滤波器.

图7 二进制小波变换信号分解示意图Fig.7 Schematic diagram of binary wavelet transform signal decomposition

当实际采样频率为300kHz时，对暂态信号进行尺度j＝5层分解后，得到小波系数为d1（n），d2（n），d3（n），d4（n）和d5（n），分别对应的频段为75～150kHz，37.5～75kHz，18.75～37.5kHz，9.375～18.75kHz和4.687 5～9.375kHz.

根据Parseval定理可知：对于正交小波基，原始信号的能量和展开系数的能量存在等价关系［13－14］.对应第j（j＝1，2，3，4，5）尺度高频信号能量Pdj为

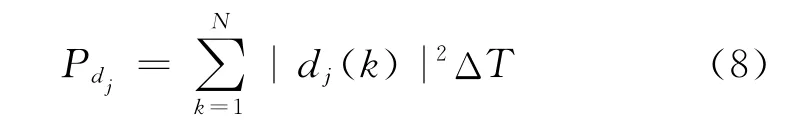
式中：N为采样点个数，ΔT为采样点间隔.

本文中经过db4小波分析提取5个尺度高频能量Pdj（j＝1，…，5）.Pd1对应75～150kHz范围内能量，Pd2对应37.5～75kHz范围内能量，Pd3对应18.75～37.5kHz范围内能量，Pd4对应9.375～18.75 kHz范围内能量，Pd5对应4.687 5～9.375kHz范围内能量.由于Pd1为谐振点所在频带内信号能量，区内和区外故障在此频带内能量差异最大.区内外故障在低频段内差异不大，故选取两个低频段内信号能量Pd4和Pd5作为参考，将谐振频段能量Pd1与低频段能量Pd4、Pd5作比较，构建能量比例系数λp1和λp2：

2.4 基于小波能谱的暂态保护流程图

基于小波能谱的暂态保护流程如图8所示.具体过程为：

（1）暂态保护实时提取电流信号，若发生突变，则启动故障判断程序，通过正交小波变换计算模极大值，判断是否模极大值越限.

（2）若越限，则利用模极大值确定故障发生时刻，然后提取故障时间段内各频段内的高频和低频信号并计算对应能量大小.

（3）计算故障判据，并延时判断故障是否依然存在，若存在则发出跳闸指令，否则返回.

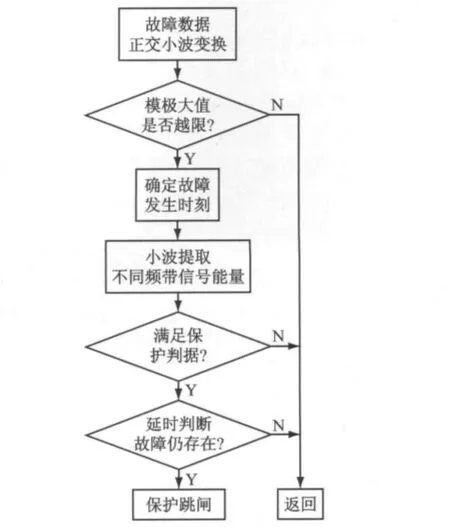
图8 基于小波能谱的暂态保护流程图Fig.8 Flow chart of transient protection based on wavelet energy spectrum

3 仿真及结果分析

为验证本文提出的基于罗氏谐振装置暂态保护方案的有效性，使用PSCAD／EMTP软件搭建仿真模型如图9所示.系统频率为50Hz，电源电压为35 kV，电源容量为10MVA，线路采用FD（frequency dependent）模型.模型仿真3段配电线路，M、N、P和Q为各段母线.对应线路NP而言，F1为区内故障，F2则为区外故障.MN、NP和PQ线路长度各为10km，根据文献［15］可知母线处电容经处理后一般选取2 000～15 000pF，因此母线对地等效电容取0.01uF.系统采样频率选300kHz，故障类型为A相接地，故障发生时刻为A相电压过零后30°，故障接地电阻大小为0.1Ω.线路边界罗氏谐振装置参数可根据1.1节设置.

图9 基于罗氏谐振装置的暂态保护仿真模型Fig.9 Transient protection simulation model based on Rogowski coil resonance equipment

3.1 故障启动元件

由于故障点处小波变换后的模极大值随着小波尺度的增大而增大，由此可确定故障发生时刻并作为故障启动元件.对仿真得到的故障信号作3尺度小波变换，提取得到的暂态电流多尺度波形如图10所示，由此可确定故障发生时刻.

图10 基于模极大值的故障时刻定位Fig.10 Fault location based on modulus maximum value

3.2 提取故障信号的高频和低频信息能量

确定故障时刻后，提取故障暂态特征明显的时间段内信号.以母线N处保护装置为例，仿真发生在F1处区内故障和F2处区外故障两种情况，分析母线N处暂态电流信号.对该区段内信号进行db4小波变换，提取故障电流不同频带信号，且通过式（8）～（10）计算能量Pdj及对应能量比例系数λp1和λp2.

表1所示为区内外故障对应各频段信号能量大小和能量比例系数.由表1可知：能量比例系数λp1和λp2在区内、区外故障情况下有较大差异，其中λp1的差异基本保持在一个数量级，具体判据需要通过对不同的故障状况统一分析后综合选择.

3.3 各种不同故障状况仿真

接下来分析不同故障类型、不同故障时刻以及不同的故障接地电阻大小情况下暂态信号能量的区别，验证本文提出保护方案在不同故障情况下的可靠性，并获得通用的保护判据.

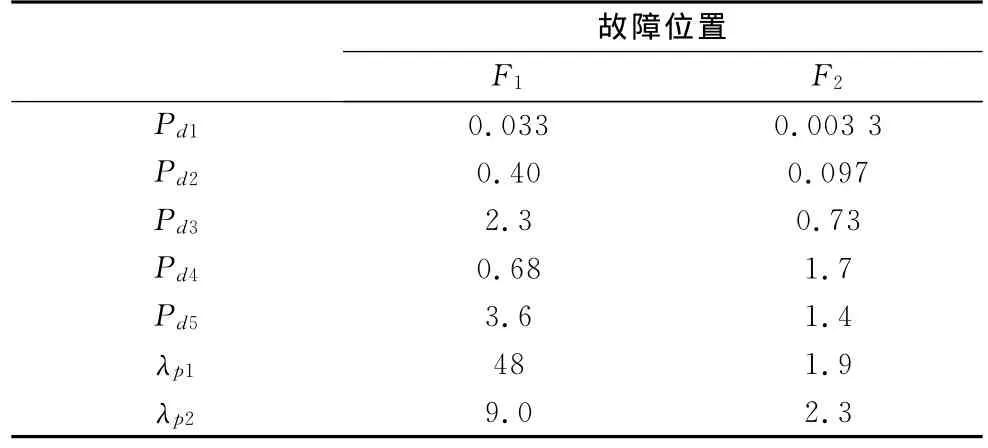
表1 不同频段暂态信号能量及能量比例系数Tab.1 Transient signal energy and energy ratio coefficient of different frequency band 10－3

3.3.1 不同故障类型

对不同故障类型AB、ABG和ABCG进行仿真，计算暂态能量和能量比例系数见表2.可以看出能量比例系数基本延续表1特征，对于不同的故障类型，设置合适的保护整定值，选取λp1和λp2作为判据均能可靠区分开区内外故障.

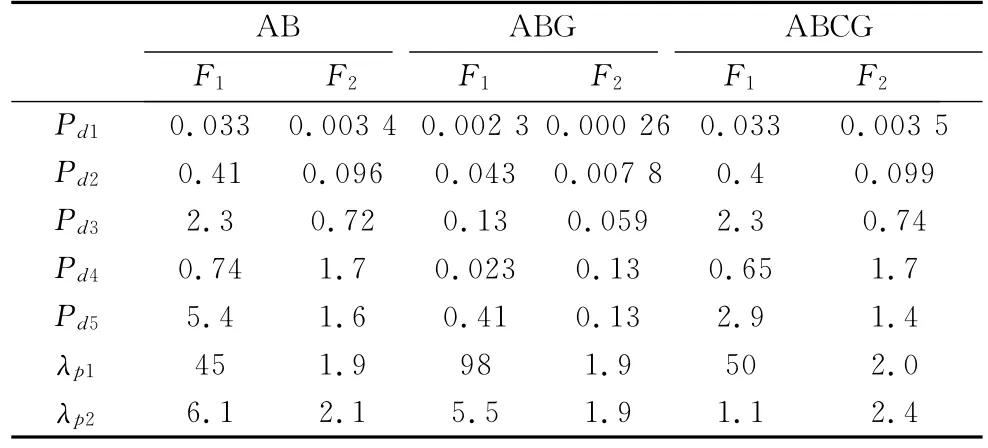
表2 不同故障类型暂态信号能量Tab.2 Transient signal energy of different fault types 10－3

3.3.2 不同故障时刻

故障发生时刻对故障暂态信号能量的影响比较大［6］.由表3可知，故障发生时刻靠近过零点时，F1和F2处接地故障对应的能量比例系数λp2差异很小.但随着故障时刻离过零点距离增大，在区内外故障对应λp2差异明显.而比例系数λp1依然保持良好的差异特性，在不同故障时刻均有数量级的区别.

表3 不同故障时刻暂态信号能量Tab.3 Transient signal energy of different fault time 10－3

3.3.3 不同故障接地电阻大小

选取不同阻值的故障接地电阻进行仿真，结果见表4.由表可知：随着故障接地电阻的增大，λp1差异减小，但是对于不同接地电阻，基本保持一个数量级差异.而λp2在不同故障接地电阻情况下，相同故障区内判据不在同一数量级，因此不能作为保护判据.

表4 不同故障接地电阻暂态信号能量Tab.4 Transient signal energy of different fault resistance

综上仿真结果，选定能量比例系数λp1作为保护判据，设定合适的整定阈值即可以可靠地区分区内和区外故障，具有很好的通用性.

4 结论

提出一种基于罗氏谐振装置和小波能谱的配电网单端暂态保护新方案，并通过PSCAD／EMTDC仿真验证了该方案的有效性.获得以下结论：

（1）在配电网边界处接入罗氏谐振装置，可以改变线路边界处暂态行波折反射系数的效果，由此区分区内外暂态行波信号.

（2）利用小波多分辨率分析可以方便地提取故障行波不同频段内的暂态信号，且谐振频带内的暂态能量在区内外故障差别最大.

（3）利用谐振频带信号能量与低频段信号能量比值作为暂态保护判据，能够可靠地区分区内外故障；该判据在不同故障类型、不同故障时刻以及不同故障电阻下都具有很好的选择性.

（4）利用配电线路的单端暂态信息，可以有效地区分区内外故障.保护的数据窗口选取故障后1／20周波，即1ms暂态电流高频分量，与传统工频保护相比，大大提升了保护的实时性、快速性.

［1］哈恒旭，张保会，吕志来.边界保护的理论基础（第一部分）：故障暂态分析［J］.继电器，2002，30（9）：7.HA Hengxu，ZHANG Baohui，LV Zhilai.The basic theories of boundary protection （Part I）：fault transient analysis［J］.Relay，2002，30（9）：7.

［2］邹积岩，段雄英，张铁.罗柯夫斯基线圈测量电流的仿真计算及实验研究［J］.电工技术学报，2001，16（1）：81.ZOU Jiyan，DUAN Xiongying，ZHANG Tie.The simulating calculation and experimental research of Rogowski coil for current measurement［J］.Transactions of China Electro technical Society，2001，16（1）：81.

［3］项经猛.负阻抗变换器的实现与应用研究［J］.襄樊学院学报，2005，23（5）：58.XIANG Jingmeng.A study of the realization and application of negative impedance converter［J］.Journal of Xiangfan University，2005，23（5）：58.

［4］周文中，赵国生，李海洋.Rogowski线圈测量误差分析及改进措施［J］.电力系统保护与控制，2009，37（20）：99.ZHOU Wenzhong，ZHAO Guosheng，LI Haiyang.Error analysis and improved method of Rogowski coil［J］.Power System Protection and Control，2009，37（20）：99.

［5］刘浩芳，王增平，徐岩，等.超高压输电线路波过程及暂态电流保护性能分析［J］.电网技术，2006，30（3）：71.LIU Haofang，WANG Zengping，XU Yan，et al.Analysis of transmission process of fault－generated travelling wave along EHV transmission lines and performance of transient current protection［J］.Power System Technology，2006，30（3）：71.

［6］史燕琨，肖湘宁，邹积岩.基于边界保护的配电网故障区段无通信定位方法［J］.电网技术，2009，33（4）：87.SHI Yankun，XIAO Xiangning，ZOU Jiyan.A noncommunication fault section location method for power distribution system based on boundary protection［J］.Power System Technology，2009，33（4）：87.

［7］陈皓.电力系统故障暂态信号的功率谱估计［J］.电力自动化设备，2002，22（6）：12.CHEN Hao.Power spectral estimation of power system fault transient signal［J］.Electric Power Automation Equipment，2002，22（6）：12.

［8］Sakis Meliopoulos A P，Lee C H.An alternative method for transient analysis via wavelets［J］.IEEE Trans on Power Delivery，2000，15（1）：114.

［9］陈小勤，何正友，符玲.基于小波能谱的电力暂态信号分类识别方法［J］.电网技术，2006，30（17）：59.CHEN Xiaoqin，HE Zhengyou，FU Ling.Electric power transient signals classification and recognition method based on wavelet energy spectrum［J］.Power System Technology，2006，30（17）：59.

［10］马丹丹，王晓茹.基于小波模极大值的单端行波故障测距［J］.电力系统保护与控制，2009，37（3）：55.MA Dandan，WANG Xiaoru.Single terminal methods of traveling wave fault location based on wavelet modulus maxima［J］.Power System Protection and Control，2009，37（3）：55.

［11］刘涛，曾祥利，曾军.实用小波分析入门［M］.北京：国防工业出版社，2006.LIU Tao，ZENG Xiangli，ZENG Jun.Practical wavelet analysis getting started［M］.Beijing：National Defense Industry Press，2006.

［12］董新洲，葛耀中，徐丙垠.输电线路暂态电流行波的故障特征及其小波分析［J］.电工技术学报，1999，14（1）：59.DONG Xinzhou， GE Yaozhong， XU Bingyin.Fault characteristic of transient current travelling waves and its analysis with wavelet transform［J］.Transactions of China Electrotechnical Society，1999，14（1）：59.

［13］范春菊，郁惟镛，Li K K.基于暂态能量的输电线路速动保护方案［J］.电网技术，2006，30（14）：77.FAN Chunju，YU Weiyong，Li K K.A transient energy based fast protection scheme for transmission lines［J］.Power System Technology，2006，30（14）：77.

［14］Megahed A I，Moussa A M，Bayoumy A E.Usage of wavelet transform in the protection of series－compensated transmission lines［J］.IEEE Trans.on Power Delivery，2006，21（3）：1213.

［15］田书，张胜朝.选择性井下高压电网行波距离保护研究［J］.工矿自动化，2008，3：19.TIAN Shu，ZHANG Shengchao.Research of selective distance protection of traveling wave for underground high voltage power network［J］.Industry and Mine Automation，2008，3：19.