一种基于贝叶斯理论的软件可靠度评估方法

许金超，曾国荪，王 伟

（1.同济大学 电子与信息工程学院，上海201804；2.同济大学 嵌入式系统与服务计算教育部重点实验室，上海201804）

软件测试是由人工或自动的方法来执行或评价系统或系统部件的过程，以验证它是否满足规定的需求，或识别出期望的结果和实际结果之间有无差别.现代软件工程中软件测试是不可缺少的一个环节.随着软件规模越来越大，软件产品的逻辑功能和系统结构越来越复杂，有限的时间和资源范围内设计和选择测试用例以获得足够的测试覆盖率变得越来越难.通过分析软件中的因果关系采用严格的测评方法评估软件是否达到可靠性目标可以为测试人员提供决策支持，因此成为了学术界和工业界的一个重要研究方向.

贝叶斯方法利用先验认识对参数进行估计这一特点使得该方法在软件可靠性的估计中得到了广泛的应用.Littlewood等［1］提出了基于贝叶斯方法的Littlewood－Verrall 模 型，Becker 和 Oikonomou等［2－3］各自给出了软件失效估计的不同贝叶斯方法.Miller等［4］提出了基于输入域的软件可靠性评估的贝叶斯方法.Cukic等［5］讨论了在利用或不利用对系统可靠性的主观认识的情况下采用贝叶斯理论对可靠性进行估计的方法.张德平等［6］给出了一种基于先验知识的快速学习算法，并利用此算法来优化测试过程，从而降低测试成本.

已有的这些评估方法难以有效地收集与表示软件失效时间数据，从而限制了这些方法在可靠性评估中的应用.并且方法都相对复杂、误差较大，测试的持续期太长，导致某些高可靠性指标的验证不易实现.工程中实用的可靠性估计方法应该能够简化计算过程，最大化复用已有的测试数据，减少测试用例的数量，为何时进行单元测试、何时进行集成测试提供决策依据.随着面向对象技术的广泛应用，大规模软件通常划分为多个模块进行开发测试，这些模块的测试结果和整个软件的测试成败有直接联系.本文通过建立软件内部模块影响关系图利用贝叶斯方法计算出模块需要的测试用例数目和每个模块的可靠度，进而评估整个程序的可靠性.该评估方法能够给出每一模块的可靠程度的精确数值且计算简单，可以直观地为测试过程提供决策依据，减少测试用例数量，解决了已有可靠性估计方法中存在的部分问题.

1 模块影响关系

软件是由软件模块构成的集合，令P表示一个软件，定义P＝｛M1，M2，M3，M4，…｝，其中M1，M2，M3，M4，…是P中的所有软件模块.

定义1 如果模块M测试出错，可能会导致模块N出错，则称M影响N，记作如果M测试出错不会导致模块N出错，则称M不影响N，记作

定义2 给定软件模块M和N，如果不存在模块K∈P，使得同时成立，则称M直接影响N，记作

定义3 程序P的模块影响关系图是一个二元组＜V，E＞，其中V代表软件中的所有模块，E表示V中模块间的直接影响关系.

对于模块影响关系图中不受其他模块影响的节点称为底层节点，除此之外的其他节点称为上层节点.一般说来，一个模块影响的模块越多，则它的测试结果对整个程序的影响越大，对它的可靠性要求就更严格，这种节点的重要性更高.图1给出了一个模块影响关系图的实例，实例中的模块选自一个游戏软件，图中每个模块对应游戏中的一个类，图中AnimatePlayer直接影响3个模块，因此上层节点AnimatePlayer的重要性比底层节点MPlayer高.

对于设计不好的软件系统，会存在软件模块间高耦合的情况，从而造成模块间出现循环依赖的影响关系，从而在模块影响关系图中出现环路.为了利用贝叶斯方法研究各个模块的测试可靠度，需要消除图中的环路.可以用2种方法消除图中的环路.第1种方法是分析具体应用程序，修改其源代码，改进程序的实现方式，消除代码间的循环依赖关系，然后重新构建模块影响关系图.在不方便修改源代码的情况下，可以采用第2种方法，这种方法将存在循环依赖关系的环上的所有节点视作一个整体，在图中作为一个单独的节点存在，然后将指向环上节点的边统一指向该节点.循环这个步骤，直至图中不出现回路.最终得到一个贝叶斯网络.

图1 模块影响关系图实例Fig.1 Example of module influence relation ship diagram

2 基于贝叶斯理论的软件测试

程序的可靠度是对整个程序成功执行的期望，而系统的成功执行意味着程序的所有模块必须全部按用户的期望执行.模块M的可靠度可以通过下次测试是否成功的概率进行估值，记模块M的可靠度为（M）.

2.1 单模块的可靠度评估

对每个单独的模块来说，测试结果只有2种：成功或者失败.单模块的软件测试是一个二项式分布，可以运用贝叶斯方法直接估计后验测试成功概率.

命题1设M为软件P中的一个模块，如果用二项事件（成功／失败）描述测试结果，当对M进行n次测试后，测试成功的次数为u，测试失败的次数为v，则模块M测试成功的后验概率服从β分布，其密度函数为

式中，θ为模块测试成功的概率，单模块M的可靠度（M）可用M第n＋1次测试成功的概率给出

式中：E（·）表示数学期望；0＜θ＜1；参数u，v＞0.

命题1为单测试模块的可靠性提供数值估算，式（2）给出了直接计算模块可靠度方法.但是一个模块可能只进行过很少几次测试，不足以用来评估目标模块的可靠度.为了拥有足够的把握确认对的估计，需要度量的置信水平.令－ε，＋ε）为的置信度为γ的置信区间，ε代表了一个可以接受的错误水平，则可用如下公式计算的置信度：

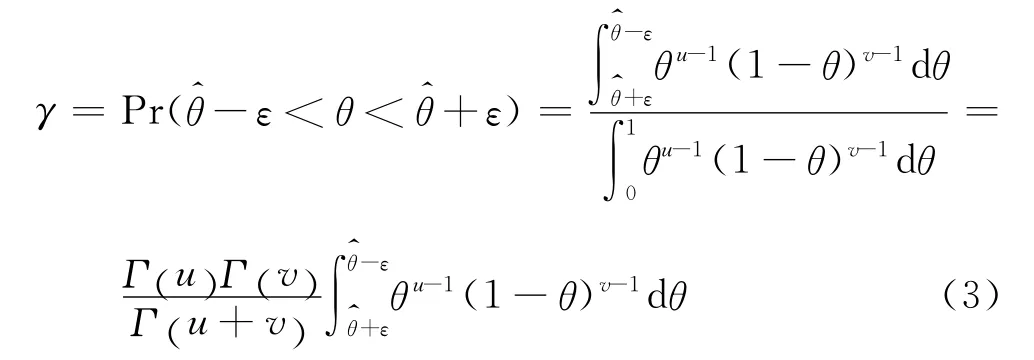
由于区间估计的置信度与精度相互制约，当测试总次数n固定时，精度与置信度不可能同时提高，为此在保证置信度前提下尽量提高精度.即先选定一个置信度阈值γ0，然后通过增加总的测试次数n提高精度，当精度达到可接受的水平，即γ≥γ0时，可根据这时的测试结果进行可靠度计算.通过推导可得到需要的样本容量n0同ε和γ0之间的关系

2.2 存在直接影响关系的2个模块的可靠度评估

若M和N为P中的2个模块，且且由命题1可以直接求得M的可靠度.观察可知N的可靠度取决于M的可靠度（M）和M测试正确的前提下N自身的可靠度，为了表述方便，将依赖于影响模块的可靠度称作推荐可靠度，记作（N），则有（N）＝（M）；将不考虑影响模块的时候自身的可靠度称作直接可靠度，记作（N），这可由式（2）进行计算.合并这二者，可得N的可靠度，由以下公式给出：

λ的选择由测试人员对两者的重要性判断给出.一般说来，对于上文中的M和N的关系，可以直观认为计算时（N）比（N）更重要.因此λ由下式给出：

式中：le为N中受M影响的代码行数；la为N中总代码行数.

2.3 多模块可靠度评估

若L，M，N是P中的3个模块此时L的可靠度取决于M和N的可靠度以及M，N测试通过前提下的可靠度.因此有

式中：（L）可以由式（2）计算得出，而（L）即M，N的联合可靠度（M，N）的评估又分2种情况.

命题2 设对M和N的总测试次数为n1和n2，其中测试成功次数为u1和u2，测试失败的次数为v1和v2.则（M，N）的估计为

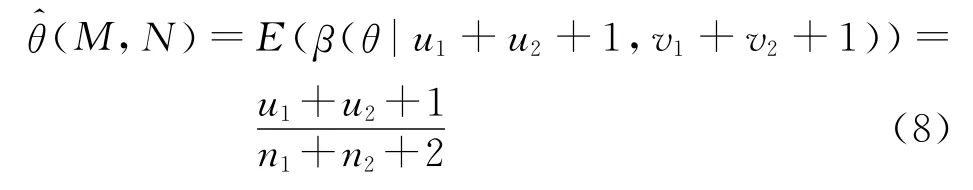
当直接影响L的模块不止一个时，不难对式（8）进行推广，同时结合前面对模块可靠度准确性分析可得

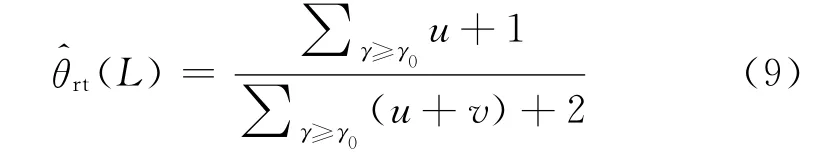
这里为了保证联合可靠度的置信水平，首先要求每个单独的模块都应该满足γ≥γ0.

这种情况下L的可靠度不仅取决于L自身的可靠度和M，N本身的可靠度，另外还和影响M，N从而间接影响L的模块的可靠度有关系.因此这种情况下对式（8）进行扩展得

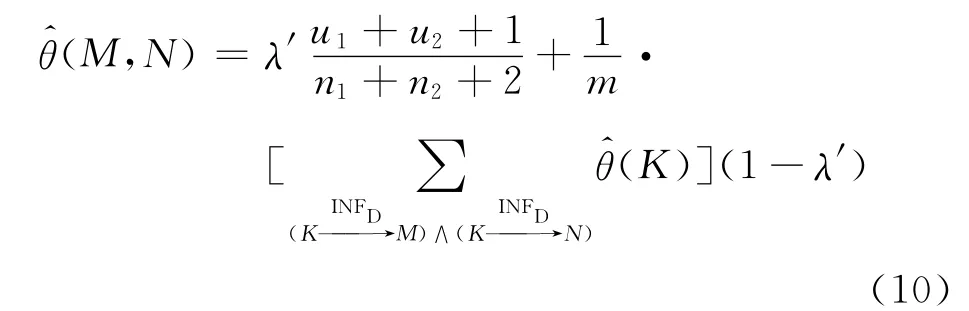
式中：m为满足条件的K的个数；λ′为M，N中除K以外的代码行数与M，N中总代码行数的比值.类似的有，当影响模块多于2个时式（10）推广为

2.4 可靠度评估在测试过程中的应用

式（1）～（11）给出了利用贝叶斯理论对软件模块可靠度进行估值的计算方法.在实际测试过程中，必须做好测试记录，它是可靠度评估的基本依据.整个测试过程描述如下：测试一个程序，首先根据程序分解后的模块间影响关系构建贝叶斯网络，统计每个模块的影响模块数量，对每个模块根据其重要程度确定置信度和置信区间，然后根据这些参数确定每个模块的用例数量并进行测试，并使用测试结果对模块的可靠度进行估值，如果可靠度达到了模块的测试要求，则认为该模块测试成功，否则对软件进行修复并产生新的测试用例继续测试.在保证程序的每个底层模块测试成功的前提下再对上层模块进行测试和可靠度计算.重复这一过程，直至所有模块可靠度都达到其设计指标.

3 应用和实验

3.1 应用示例

该框架曾应用在一款Android平台手机游戏的自动化测试中，测试游戏由Java开发，共有25个模块组成，根据各个节点间影响关系构建的贝叶斯网络有8个底层节点，17个上层节点.测试过程中，设定所有模块的置信度阈值为0.98，设定模块AnimatePlayer，NpcPlayer和Effect可以接受的错误水平ε＝0.12，则由式（4）可计算出n0＝159.896，即需要的测试用例至少为160个；模块EnemyPlayer的ε＝0.08，至少需要测试用例360个；其他模块的ε＝0.15，至少需要测试用例103个.选择其中的一部分模块来描述模块可靠度的计算过程，选择的部分模块之间的影响关系如图1.表1给出了最底层节点的测试成功次数和失败次数以及计算出的底层节点可靠度.可以看到全部满足可靠度阈值，因此可以继续进行上层节点的可靠度计算.

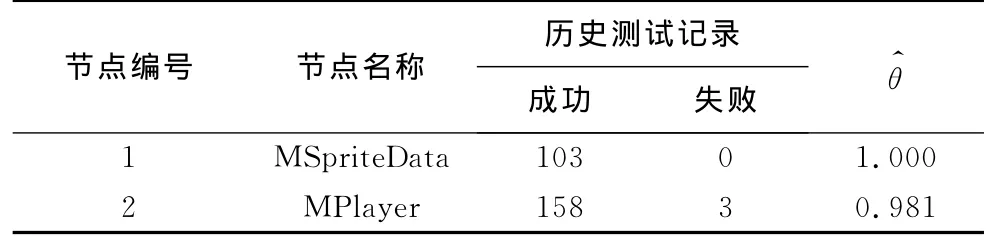
表1 底层节点测试数据和可靠度Tab.1 Test data and reliability of bottom nodes

经观察，MPlayer共56行，MSprite共有代码132行，和MSpriteData类相关代码15行.可以求得λ1＝0.886，故（MSprite）＝0.114×1＋0.886×0.990＝0.991.AnimatePlayer类中共有代码1 543行，和MPlayer和MSprite相关的代码有116行，因此其他模块可靠度见表2，最终得（GameCenter）＝0.981，可知这部分模块和整个程序的可靠度全部大于阈值，测试通过.

表2 上层节点测试数据和可靠度Tab.2 Test data and reliability of upper layer nodes

3.2 实验分析

为了验证本文的可靠度评估方法用于指导软件测试时的优势及是否能够有效提高软件测试的效率和成本，进行了该方法与随机测试策略、学习策略［6］的比较.在随机测试策略中测试用例根据均匀分布随机地在测试用例集中选取，也就是说，每一个可行的测试用例行动在测试中都以相同的机会被选取.学习策略是一种基于Markov决策过程的策略，它运用交叉嫡的方法搜索最优的测试剖面，从而优化软件测试，减少测试用例数.实验中测试目标是目标程序最终测试失败的概率低于3%，实验过程中采用10个不同的测试用例集分别进行了10次测试，10次测试中分别达到这一要求时3种方法分别使用的最小用例数目如图2所示.

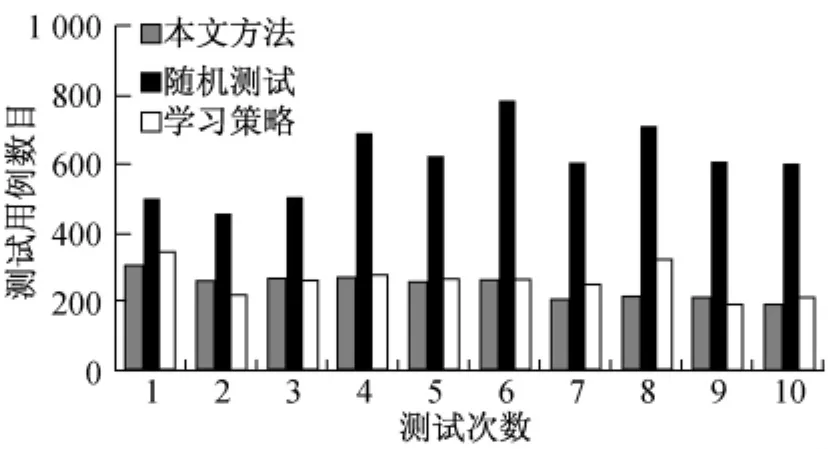
图2 3种测试策略的测试成本Fig.2 Test cost of three testing strategies

10次测试实验中本文方法的平均测试用例数为242.9，和学习策略基本持平，随机测试的平均测试成本在三者中最高为608.3.测试结果表明，本文给出的方法在用于软件测试时虽然不能保证每次测试成本都比随机测试小，但其平均测试成本会远远低于随机测试的平均成本.实验过程中得知，同学习策略相比，尽管在测试成本上并不占太大优势，然而本文方法实现更为简单，计算快速直观，测试用例数目相对保持稳定，能够缩短测试的总时间.

在整个项目的测试过程中使用该评估方法能够准确把握各模块的可靠程度，从而有针对性地设计测试用例，减少了不必要的测试，缩短了项目的交付时间.

4 结语

通过分析软件模块间的影响关系，基于测试数据，利用贝叶斯方法为各个软件模块计算一个数值表示的可靠度.通过模块间的影响关系，并对可靠度进行排序，可以确定测试过程中要重点测试的模块，减少不必要的测试.该方法不但能快速准确地得到评估结果，也可以为模块的测试用例数量提供参考.

［1］Bev Littlewood，John Verrall.A Bayes reliability model with a stochastically monotone failure rate［J］.IEEE Transaction on Reliability，1976，23：108.

［2］G Becker，L Camarinopoulos.A Bayesian estimation method for the failure rate of a possibly correct program［J］.IEEE Transaction on Software Engineering，1990，16：1307.

［3］Kostas Oikonomou.Predictive with the dynamic Bayesian gamma mixture model［J］.IEEE Transaction on Systems，Man and Cybernetics，1997，27：529.

［4］Keith Miller，Larry Morell，Noonan Park，et al.Estimating the probability of failure when testing reveals no failures［J］.IEEE Transactions on Software Engineering，1992，18（1）：33.

［5］B Cukic，D Chakravarthy.Bayesian framework for reliability assurance of a deployed safety critical system［C］／／Proceedings of the 5th IEEE International Symposium on High Assurance Systems Engineering.New York：Computer Society，2000：321－329.

［6］张德平，聂长海，徐宝文.基于Markov决策过程用交叉熵方法优化软件测试［J］.软件学报，2008，19（10）：2770.ZHANG Deping，NIE Changhai，XU Baowen.Cross－entropy method based on Markov decision process for optimal software testing［J］.Journal of Software，2008，19（10）：2770.