大跨径三塔缆索承重桥力学与经济性能

周云岗，肖汝诚

（同济大学 土木工程学院，上海200092）

20世纪末以来，大跨度缆索承重桥发展迅速，斜拉桥进入了超千米级时代，悬索桥也将实现3 300m超长跨径.然而，随着跨径的增大，传统缆索承重桥将面临诸如静动力稳定性下降、缆索利用效率变差等问题［1－3］.为克服这些难题，设计师们提出了组合缆索承重桥和多塔缆索承重桥等方案.组合缆索承重桥，如日本备赞濑户大桥、美国旧金山－奥克兰西海湾桥等，若中部无岛屿，须在江海中修建索塔、辅助墩或锚碇等构件，不利于通航，且造价较高，而多塔缆索承重桥建造了多个中塔，既提高了通航能力，降低了造价，又减少了水中作业，降低了施工难度，在海峡工程应用中具有技术优势［4］，是未来缆索承重桥发展的一个重要方向.

近年来，越来越多的多塔缆索承重桥应用于工程实践，结构体系的研究成果也逐渐增多.多塔悬索桥方面，文献［5］研究了主跨为3 000m的三塔悬索桥静力稳定性和颤振特性.文献［6］以智利查考桥设计方案为背景，比较了三塔悬索桥与共锚悬索桥的结构特点.文献［7］和［8］通过力学参数研究分别阐述了主跨为2 000m和1 545m的三塔悬索桥的力学特点.文献［9］阐述了韩国新千年桥的概念设计.多塔斜拉桥方面，文献［10］通过参数分析和气动选型研究了香港的青马大桥的气动稳定性.文献［11］研究了多塔斜拉桥的非线性特性和稳定性.文献［12］提出了钢与混凝土混合型桥塔，并将之应用于多塔斜拉桥，研究了主跨为200m的七塔八跨斜拉桥的静动力特性.文献［13］论述了提高多塔缆索承重桥整体刚度的措施.文献［14］研究了三塔协作体系的竖向刚度等.多塔协作桥方面，文献［15］针对西海峡通道从概念上初步对比了传统悬索桥、三塔悬索桥和三塔斜拉桥的优缺点.然而，当前研究成果大多局限于特定桥型，且研究内容集中在结构的力学性能方面，对上述3种桥型缺乏全面系统的对比.

针对上述问题，笔者首先以主跨为1 400m三塔缆索承重桥的3种桥型为研究对象，全面系统地对比研究三者的力学性能、经济性能和施工方法，获得三塔缆索承重桥的推荐桥型.

1 力学性能研究

1.1 研究方案

1.1.1 研究的思路

桥型体系力学性能研究的目的是摸清各种桥型的综合力学特点及其适用范围，为桥型选择及方案试设计提供依据.研究各种桥型：①力学特征；②关键部位力学响应的量化关系；③存在的关键力学问题；④静力稳定性是否可能控制设计；⑤自振特性具有哪些规律，对抗风抗震有哪些影响等.

建立三维有限元分析模型，研究3种桥型在典型荷载下的力学响应最终给出三者的力学特点.特别说明，3种桥型梁、塔的截面几何特性相同.由于桥型体系研究的重点是各桥型之间的定性关系及同桥型的力学特点，核心是梁、塔，而其截面几何特征对整体力学特征影响较小.因此，采用相同的截面既能使计算结果正确地反映其力学，又能使其响应值更具可比性，并为方案试设计提供参考，如选择合适的材料、构形和几何特性.

1.1.2 模型的建立

根据传统大跨径缆索承重桥的工程实例及科研成果，初步拟定3种桥型的总体布置方案如图1所示，重要的结构参数如表1所示，表中Ls为边跨跨径，Lm为中跨跨径，f为主缆名义垂度，H为索塔总高，h为桥面以上塔高.边界条件方面，3种桥型主梁的横向自由度与索索塔和主梁的典型截面几何特性如表2所示.塔横梁或辅助墩耦合，竖向自由度与辅助墩或悬索桥的边塔横梁耦合，释放纵向自由度.主缆的锚点、索塔及辅助墩的底部均固结.

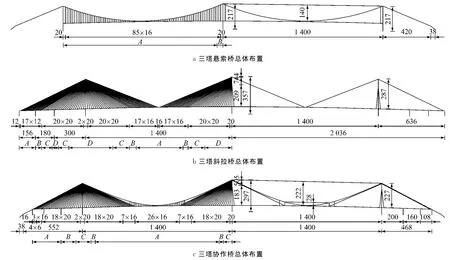
图1 三塔缆索承重桥立面布置（单位：m）Fig.1 Elevation of three－tower cable－stayed supported bridge（unit：m）

结构的材料根据已有工程实例确定，主要构件的材料为：索塔采用C50混凝土；辅助墩采用C40混凝土；主梁采用Q370qd钢材；主缆采用预制平行钢丝索股，每股由Φ5.3mm镀锌高强钢丝组成，钢丝标准抗拉强度为1 860MPa，运营状态安全系数为2.5；斜拉索采用Φ7mm镀锌平行钢丝成品索，抗拉强度1 770MPa，运营状态安全系数为2.5；吊索为销接式，采用Φ5mm镀锌高强预制平行钢丝束，抗拉标准强度为1 670MPa.

表1 各种桥梁体系的结构参数Tab.1 Structure properties of three bridges m

表2 塔、梁典型截面参数Tab.2 Properties of typical cross－sections

缆索承重桥是由塔、梁、索组成的柔性结构，属于高次超静定结构，缆索的初始内力直接影响着结构体系的表现.在研究其力学特性时必须首先确定结构的合理成桥状态，计算出较优的初始缆索力，以此状态作为结构分析的基础.结构分析采用更新的拉格朗日列式（U.L列式）的有限位移理论［3］，主梁和索塔采用非线性梁单元模拟，斜拉桥和协作桥的斜拉索采用8段杆单元模拟，恒载索力优化采用基于ANSYS的1阶方法.

1.1.3 工况的选择

一般公路桥梁跨径越大恒载所占比重越大，因此在恒载作用下结构内力响应是衡量其力学性能的重要指标之一，对于缆索承重桥表现为合理成桥状态的确定.活载是桥梁结构的基本可变荷载，其响应与加载形式有关，即按最不利位置加载.同时，结构整体升降温时主梁和缆索系统产生较大的伸缩量，直接或间接地迫使主塔偏位、主梁挠曲，进而造成较大的内力响应.此外，大跨径缆索承重桥的迎风面较大，极限静阵风作用时结构静阵风效应较大，往往会成为控制设计的主要因素.由此，着重考察上述4种典型工况，具体如表3所示.

构荷载设计值参照苏通长江大桥、泰州长江大桥和舟山连岛工程等大型桥梁的设计条件确定，具体取值为：一期恒载按材料密度确定，二期恒载按70 kN·m－1考虑；汽车荷载采用公路－Ⅰ级，按双向8车道计算；设计基本风速根据我国交通规划情况，按江浙沪长江沿线及沿海连岛工程、广东沿海及琼州海峡等地区确定，根据《公路桥梁抗风设计规范》（JTG／T D60－01—2004）附录表 A，100年一遇条件下，上海基本风速为33.8m·s－1，舟山为40.5 m·s－1，湛江为39.4m·s－1，海口为38.4m·s－1.假定取最不利荷载计算，即假定设计基本风速为40.5m·s－1.

表3 典型荷载工况Tab.3 Typical load case

1.2 静力特性

1.2.1 恒载效应对比

考虑几何非线性，经索力优化后，获得3种桥型的合理成桥状态.主梁恒载应力如图2所示.总体上，三者的主梁弯矩基本相等，其值取决于索距，而主梁轴力相差很大.斜拉桥主梁的最大轴压力为349 MN，约为协作桥的1.7倍，而悬索桥主梁的轴力基本为零.由此，恒载作用下，斜拉桥主梁的上、下缘应力基本相等，约为协作桥的2倍，而远大于悬索桥.

图2 3种桥型主梁恒载应力Fig.2 Stress diagram of beam due to dead load

索塔恒载应力如图3所示.恒载作用下，3种桥型索塔的弯矩较小，均以受压为主，且相差不大.悬索桥的边、中塔塔根轴力分别为1 010，1 010MN，斜拉桥分别为1 310，1 280MN，协作桥分别为1 180，1 160MN.可见，三者相差不大，差值主要由索塔高度不同引起的.索塔的应力图体现了索塔的内力特征.

1.2.2 活载效应对比

活载作用下，3种桥型的主梁应力和挠度包络如图4所示.3种桥型的主梁活载轴力均较小，而主梁活载弯矩较大.悬索桥最大轴力和弯矩为12.7MN，228MN·m，斜拉桥为49.3MN，296MN·m，协作桥为43.2MN，186MN·m，对应的轴应力和上下缘弯曲应力分别为5，47和69MPa，19，61和89 MPa以及17，39和56MPa.可见，活载作用下，主梁的弯曲应力占主导地位，故主梁应力包络图与主梁弯矩包络图相似.由主梁应力图可知，斜拉桥主梁不利受力位置为最外侧4～6根斜拉索范围内和边跨辅助墩处，协作桥为拉吊过渡区和辅助墩处，悬索桥为中塔处.

图3 3种桥型索塔恒载应力Fig.3 Stress diagram of tower due to dead load

3种桥型的活载挠度最大值基本位于同一区域，悬索桥最大挠度为2.25m、斜拉桥为3.26m、协作桥为2.63m.可见，相同条件下，三塔悬索桥刚度较大，这是因为斜拉体系的斜拉索垂度效应较大，降低了结构的刚度.中塔主缆抗滑移稳定性方面，悬索桥主缆抗滑移系数为2.3，协作体系为1.6，小于规范容许值2.5.可见，悬索桥主缆的抗滑移性能优于协作桥.

索塔活载应力包络如图5所示，3种桥型的索塔轴力基本相等，而弯矩相差较大.边塔方面，悬索桥和协作桥以受压为主，斜拉桥以受弯为主，体现了悬索体系的边主缆对边塔的约束作用.中塔方面，三者均以受弯为主，且悬索桥塔根弯矩值最大.悬索桥中塔的塔根弯矩为±7 360MN·m，斜拉桥为±4 950 MN·m，协作桥为±6 490MN·m，悬索桥比斜拉桥大约33%，比协作桥大约12%.索塔应力图反映了其受力特点.根据中塔的受力特点，悬索体系的中塔适宜选用抗弯性能较佳的钢材.

1.2.3 均匀升温效应对比

全桥均匀升温30℃时3种桥型的主梁应力如图6所示.总体上，3种桥型主梁的受力特征基本相同，由温度产生的轴力很小，而弯矩较大.悬索桥主梁弯矩最大值位于中塔附近，为59MN·m，斜拉桥和协作桥位于第3个辅助墩处，分别为71MN·m和164MN·m.可见，协作桥的主梁温度效应较大，比斜拉桥大约57%，比悬索桥大约178%.

图4 3种桥型主梁活载包络Fig.4 Envelope diagram of beam due to live load

图5 3种桥型索塔活载包络Fig.5 Envelope diagram of tower due to live load

均匀升温时3种桥型的边、中塔表现出不同的受力特性，如图7.3种桥型的中塔因位于对称中心，温度效应很小，而边塔的温度效应较大.斜拉桥边塔塔根弯矩为2 225MN·m，悬索桥为1 320MN·m，协作桥为1 090MN·m.斜拉桥边塔塔根弯矩比悬索桥大约41%，比协作桥大约51%.究其原因，均匀升温时斜拉桥的主梁伸长，通过斜拉索拉动边塔向边跨偏转，从而产生较大的弯矩.悬索桥的主缆伸长，垂度增大，主缆轴力减小，且边塔减小较大，使其向中跨偏转，从而产生较大的弯矩.对于协作桥，斜拉索和主缆对边塔作用相互抵消，且主缆伸长时，悬吊部分的荷载卸给了斜拉部分，也抵消了边跨斜拉索对边塔的部分作用效应，故其边塔塔根的弯矩最小.

图6 3种桥型主梁的温度应力Fig.6 Stress diagram of beam due to temperatures

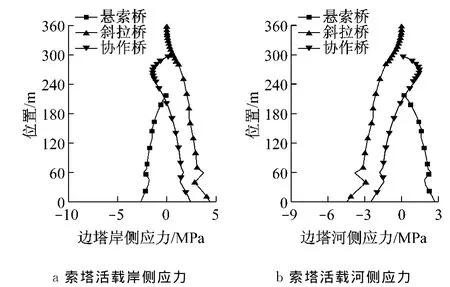
图7 3种桥型索塔的温度应力Fig.7 Stress diagram of towers due to temperatures

1.2.4 极限静阵风效应对比

在纵向静阵风作用下3种桥型的主梁响应规律与温度荷载作用下的情况类似.不同的是，斜拉桥在第3个辅助墩处的弯矩大于协作桥，分别为95 MN·m和58MN·m，而悬索桥在中塔处的最大值为28MN·m.索塔受力方面，3种桥型的受力特征相似，应力如图8.边、中塔的塔根弯矩较大，悬索桥为323，1 140MN·m，斜拉桥为4 910，3 250MN·m，协作桥为1 590，1 800MN·m.可见，悬索桥边中塔的塔根弯矩相差最大，达253%，而协作桥相差最小，为13%左右.此外，斜拉桥的纵向静阵风效应最大.这是因为斜拉桥采用全飘体系，纵向无约束，索塔变形较大，而悬索桥和协作桥的边缆有效地控制了结构纵向变形，故其内力响应较小.

图8 索塔纵向静阵风应力Fig.8 Stress diagram of towers due to longitudinal wind load

在横风静阵风作用下3种桥型的结构响应特征相同.主梁表现为连续梁的受力特征，3种桥型主梁的静横风弯矩基本相等.索塔受力方面，协作桥边中塔塔根弯矩最大，分别为2 477，2 615MN·m，斜拉桥分别为2 160，2 330MN·m，悬索桥分别为1 470，2 290MN·m.可见，协作桥边中塔的塔根弯矩比斜拉桥分别大13%，11%，比悬索桥分别大41%，12%.索塔横向静阵风应力如图9.由于塔顶的主缆横向力矩大于分散在塔身的斜拉索，而斜拉桥的索塔高度最大，故其塔根弯矩稍大于悬索桥，而协作桥的塔高较悬索桥大得多，故其塔根弯矩最大.

图9 索塔横向静阵风应力Fig.9 Stress diagram of towers due to horizontal wind load

1.2.5 计算结果综合比较

前面着重探讨了3种桥型的梁塔在各典型工况作用下的内力响应特点.研究表明，在恒载作用下3种桥型的主梁受力各异，而索塔受力相同.在其他工况下3种桥型的主梁和索塔均产生较大的弯矩，而轴力较小.各种工况作用下3种桥型的梁塔最不利受力部位相同，主梁位于边中塔、跨中及边跨辅助墩处，索塔位于塔根处.梁、塔的应力图反映了结构的响应特征.

由表4可知，边塔塔根应力方面，在各种工况下斜拉桥最大，比悬索桥大约45%，比协作桥大约35%.中塔塔根应力方面，活载作用下悬索桥最大，比斜拉桥大约30%，比协作桥大约15%；其他工况下斜拉桥最大，比悬索桥大约40%，比协作桥大约13%.可见，悬索体系中塔的活载拉应力很大，设计时须特别关注.

考虑到斜拉体系在边、中塔处主梁的控制应力相差不大，表5中仅列出中塔处主梁应力和主梁最大应力值，由表可见，在中塔位置斜拉桥主梁的活载效应和均匀升温效应最小，比悬索桥分别小500%和300%左右，比协作桥分别小57%和250%左右.其他工况下斜拉桥最大.主梁应力方面，斜拉桥应力峰值普遍大于另2种桥型，比悬索桥大90%左右，比协作桥大40%左右.

表4 各工况下3种桥型的索塔应力Tab.4 Stress of towers of three bridges under varied loads

表5 各工况下3种桥型的主梁应力Tab.5 Stress of three bridges beams under varied loads

1.3 静力稳定性

随着跨径的增大，缆索承重桥结构的稳定性显得越来越重要，开展包括主梁、索塔在内的整体结构的静力稳定性评估是全面把握大桥整体安全度的重要环节.特别是随着跨径的增大，结构在给定风速作用下可能发生静风失稳.表6给出了3种桥型在不同荷载条件下的弹性稳定分析结果，图10为3种桥型的1阶失稳模态.从表6可见，成桥后各种荷载作用下悬索体系的稳定性最好，而斜拉体系最差，原因在于斜拉体系主梁承担较大的轴向压力，导致结构稳定性下降.从1阶失稳模态来看，悬索桥为中塔面外屈曲，斜拉桥和协作桥为主梁面内屈曲.由于中塔抗弯刚度很大，所以悬索桥弹性稳定系数远高于另2种桥型.

1.4 动力特性

桥梁结构的自振频率和振动模态是进一步分析结构抗震、抗风、车振的基础.反映大跨径桥梁动力特性的重要振型为主梁的1阶竖弯、1阶纵飘、1阶扭转和1阶横弯.表7给出了3种桥型重要振型的1阶频率.3种桥型的前3阶振型相似，分别为1阶对称侧弯、1阶反对称侧弯和1阶纵飘，1阶竖弯伴随1阶纵飘出现，然后才出现1阶扭转振型，扭转振型中伴有其他振型的耦合成份.对比3种桥型的自振频率发现，3种桥型的自振频率均较小，表明结构刚度偏柔性，就抗震性能而言，结构受地震控制的可能性很小，但位移较大，宜采取相关对策，如设置限位装置.扭弯频率比是衡量结构颤振稳定性的重要参数，其值越大越好［16］.斜拉桥最大为4.6，悬索桥为2.9，协作桥为4.2，斜拉桥比悬索桥大37%左右，比协作桥大8%左右.因此，斜拉桥的颤振稳定性较佳，而协作体系也优于悬索体系.

表6 各种荷载作用下3种桥型的稳定性对比Tab.6 Comparison results of the stability of the three types under varied loads

图10 3桥桥型1阶弹性失稳模态Fig.10 First order instability mode of three bridges

2 经济性能研究

2.1 研究方法概述

文献［17］根据缆索承重桥的结构受力特点，简化估算了索塔、主梁和缆索等主要受力构件的内力响应，再结合材料容许应力，估算构件的截面面积，进而获得全桥的工程材料总量.该方法能有效地评估缆索承重桥经济性能的总体趋势.然而，估算所作的假定与实际不可避免存在一些差异，如受力模式、结构线形和极限状态等.此外，结构的刚度、静力稳定性或气动稳定性往往成为控制设计的主要因素.这些对估算成果均产生较大的影响.

表7 3种桥型的自振特性对比Tab.7 Compared results of natural vibration characteristics of the three systems

工程实践中，进行方案比选时通常根据地质地形条件选择几种合适的桥型实施方案试设计，获得切实可行的试设计方案，再统计各方案工程量，进行经济性能比较.根据这一思路，在上述3种桥型方案的基础上根据力学性能研究成果进行方案试设计，并以试设计成果为基础，进行经济性能研究.

2.2 方案试设计

3种桥型的结构总体布置如图1所示.根据力学性能研究成果对上节桥梁方案主要受力构件的材料和截面几何特性作一些调整.索塔方面，悬索桥和协作桥的中塔为压弯构件，且弯曲应力较大，因此采用钢塔，材料为Q370qd钢材，底部一定范围采用Q420qd钢材.主梁方面，斜拉桥和协作桥在索塔两侧一定范围内主梁受力较大，因此加大索塔处主梁的顶底板厚度且向两侧逐渐过渡为标准截面；悬索桥在中索塔附近受力最不利，因此加大该部位主梁顶底板厚度.图1中A，B，C，D区域对应相应的梁段.此外，悬索桥和协作桥的主梁挠度较小，而中塔主缆抗滑移性能较差，表明中塔抗弯刚度太大，应予以适当降低.

主梁和索塔的结构布置如图11～13，典型截面特性如表8.表中S为截面面积，Iy为面内抗弯惯性矩，Ix为面外抗弯惯性矩，Iz为截面抗扭惯性矩.

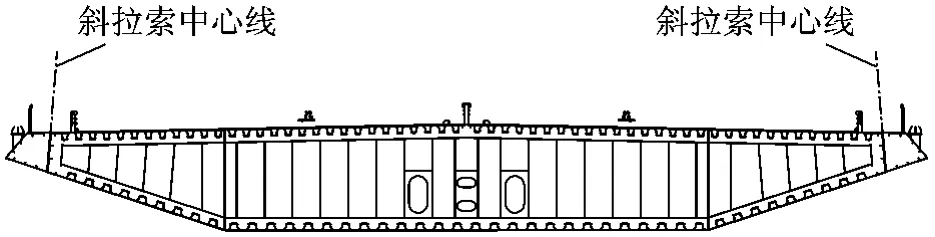
图11 主梁标准断面Fig.11 Section of girder beams

图12 混凝土塔布置及标准断面Fig.12 Shape and section of concrete town

图13 钢塔布置及标准断面Fig.13 Shape and section of steel town

应用有限元软件ANSYS计算分析悬索桥、斜拉桥和协作桥3种桥型的试设计方案得到控制性计算结果为：在静力荷载作用下，3种桥型边塔塔根基本组合应力依次为－14.2与－7.8MPa，－22.0与－3.0MPa，－14.0与－7.0MPa；中塔塔根基本组合应力依次为176.0与－299.0MPa，－13.0与－6.0MPa，122.0与－258.0MPa；主梁基本组合应力依次为116.0与－114.0MPa，－12.0与－178.0MPa，－108.0与－159.0MPa；极限横风作用下主梁应力依次为260.0与－256.0MPa，161.0与－343.0MPa，177.0与－299.0MPa；3种桥型主梁最大活载挠度依次为－4.9，－3.0，－6.7 m，挠跨比依次为1／285，1／466，1／209；3种桥型的静力稳定系数依次为14.451，4.889，6.294；3种桥型的颤振临界风速依次为45，103，59m·s－1，对应的检验风速为87m·s－1；中塔主缆抗滑移系数方面，悬索桥为3.1，协作桥为1.4.

表8 索塔和主缆典型截面特性Tab.8 Property of tower and beam of three bridges

上述分析表明，结构强度、刚度和静力稳定性稳定性方面，除局部位置外，3种桥型均能满足设计要求；颤振稳定性方面，悬索桥和协作桥须采取风振控制措施；中塔主缆抗滑移方面，协作桥须探寻有效的解决对策.

2.3 经济性能对比

进行工程造价计算时，缆索、主塔及主梁等主要构件的单价指标来源于对某大型桥梁工程方案及概算表的分析，如表9所示.由于本文着重讨论上部结构，而锚碇、桥墩和索塔基础材料用量的影响因素很多，难以准确估算，因此本文采用文献［18］的方法来估算，即认为锚碇、桥墩和索塔基础等下部结构材料用量由所承受的拉力和竖向力确定，引入相应的比列系数，即表9中锚碇材料用量比例、桥墩材料用量比例和主塔基础材料用量比例.

采用表9中的参数计算得到3种桥型试设计方案的总造价.表10为3种桥型的结构参数和总造价.表中α为构件造价小计，β为α占总造价的百分数，Σ为总造价，ρ为桥梁单位面积造价.表11为3种桥型各构件的材料用量和相应的造价，可见：

（1）就全桥总造价而言，协作桥经济性最好，其次是悬索桥，最差是斜拉桥.协作桥总造价约为斜拉桥的71.0%，为悬索桥的88.9%.

（2）对于单位桥面平均造价，协作桥最低，悬索桥较高，增加约13.4%，斜拉桥最高，增加约22.6%.

（3）缆索体系总造价方面，悬索桥为14.54亿元，斜拉桥为6.379亿元，协作桥为9.685亿元，分别占总造价的17.6%，6.2%和13.2%.可见斜拉桥缆索效率最高，而悬索桥最差.

（4）主梁造价方面，斜拉桥最高；协作桥次之，节省约26.3%；悬索桥最低，节省约49.5%.

（5）塔墩造价方面，悬索桥最低；协作桥次之，增加约64.7%；协作桥最高，增加约137.1%.

（6）锚碇造价昂贵，其占总造价的比例是评价缆索承重桥经济性的一个重要指标，悬索桥、协作桥分别约为39.8%，13.4%.

（7）同一方案中，上、下部造价分配方面，下部结构所占比重较大，悬索桥、斜拉桥、协作桥分别约为64.3%，62.7%，55.4%

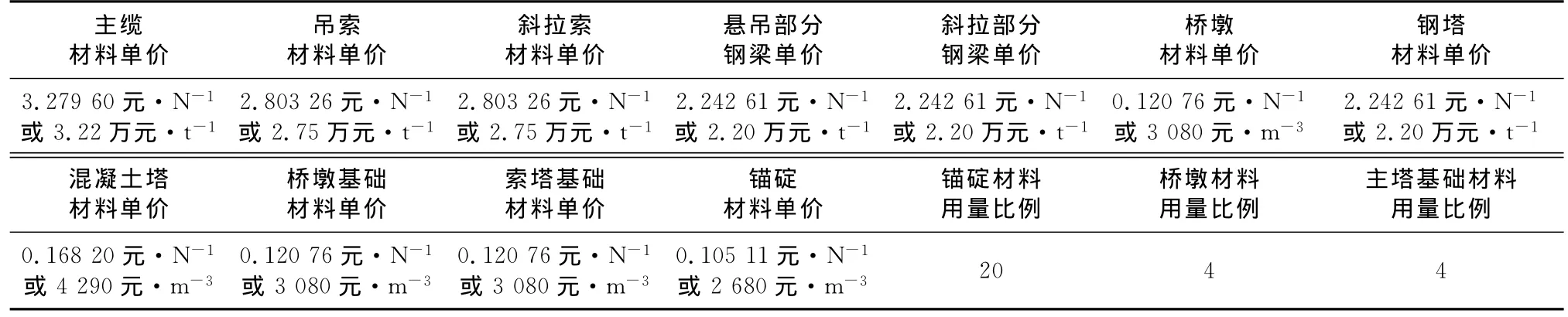
表9 缆索承重桥造价基本参数Tab.9 Parameter for total price of cable supported bridge

表10 3种桥型的结构参数和总造价Tab.10 Structure parameter and total price of three bridges

表11 3种桥型各构件的材料用量和造价Tab.11 Material consumption and price of members of three bridges

3 结论

对于主跨为1 400m级三塔缆索承重桥的3种桥型，可得如下结论：

（1）三塔协作桥的中塔主缆抗滑移性能较差，较难满足设计要求.

（2）三塔悬索桥的索塔轴力略小于另2种桥型，而主梁轴力基本为零，故具有更好的稳定性.与三塔斜拉桥相比，三塔协作桥的主梁轴力大幅减小，稳定性较好.

（3）三塔斜拉桥的自振频率与三塔协作桥相近，其扭弯频率比略大于三塔协作桥，而明显大于三塔悬索桥.

（4）三塔协作桥的总造价和单位面积造价最低，其他经济指标均处于中等水平.总体上，三塔协作桥经济性能较佳，三塔悬索桥次之，三塔斜拉桥最差.

（5）三塔悬索桥的施工工艺较为成熟，施工期间结构稳定性较佳.与之相比，三塔斜拉桥的施工难度最大，而三塔协作桥介于两者之间.

［1］Clemente P，Nicolosi G，Raithel A.Preliminary design of very long－span suspension bridges［J］.Engineering Structures，2000，22（12）：1699.

［2］张杨永，肖汝诚.超大跨度V塔斜拉桥的经济与力学特性［J］.同济大学学报：自然科学版，2009（10）：1319.ZHANG Yangyong，XIAO Rucheng.Economic and mechanical properties of super－long span cable－stayed bridge with v－shaped pylon［J］.Journal of Tongji University：Natural Science，2009（10）：1319.

［3］肖汝诚，项海帆.斜拉－悬吊协作体系桥车学特性及其经济性能研究［J］.中国公路学报，1999，12（3）：43.XIAO Rucheng，XIANG Haifan.Mechanics characteristics and economic performances study for cable－stayed suspension bridges［J］.China Journal of Highway and Transport，1999，12（3）：43.

［4］杨进.多塔多跨悬索桥应用于海峡长桥建设的技术可行性与技术优势［J］.桥梁建设，2009（2）：36.YANG Jin.Technical feasibility and advantages of appliying multi－tower and multi－span suspension bridge to construction of long bridge across straits［J］.Bridge Construction，2009（2）：36.

［5］Makoto－Kitagawa，Nobuyuki－Kashima，Susumu－Fukunaga，et al.Stability studies of ultra－long four span suspension bridge［C］／／International Association for Bridge and Structure Engineering Conference.Seoul：IABSE，2001：128－129.

［6］Torben－Forsberg.Multi－span suspension bridges［J］.Steel Structure，2001，1：63.

［7］Osamu Yoshida， Motoi Okuda，Takeo Moriya.Structural characteristics and applicability of four－span suspension bridge［J］.Journal of Bridge Engineering.2004，9（5）：453.

［8］HO Choi，HO Sungna，SUN Gilgwon，et al.A parametric study on the ultimate behaviors of multi－span suspension bridges［C］／／34th International Symposium On Bridge and Structure Engineering.Venice：IABSE，2010：54－61.

［9］JUNG Jaeho，KIM Jaehong，BAEK Jonggyun，et al.Practical design of continuous two main－span suspension bridge in Korea［C］／／34th International Symposium on Bridge and Structure Engineering.Venice：IABSE，2010：62－69.

［10］King P，Davenport A G，Schlaich M.Wind engineering studies for the Ting Kau Bridge，Hong Kong［C］／／Proceedings of the 1997 15th Structures Congress.Portland：ASCE，1997：175－179.

［11］Bakhoum M M，Helmy G，Attia W A，et al.Non－linear behaviour，failure loads and inelastic buckling of multispan cable－stayed bridges ［C ］／／Proceedings of the Eight International Conference on Civil and Structural Engineering Computing.Vienna：Civil－Comp Press Limited，2001：193－194.

［12］Y－Okamoto，S－Nakamura.Static and seismic studies on steel／concrete hybrid towers for multi－span cable－stayed bridges［J］.Journal of Constructional Steel Research，2011，67（2）：203.

［13］M－Virlogeux.Bridges with multispan cable－stayed spans［C］／／International Association for Bridge and Structural Engineering Conference.Switzerland：IABSE，1999：16－17.

［14］Haijun W，Yukitake S， Akira H，et al.Displacement characteristics of compound bridge of suspension bridges and cable－stayed bridges［C］／／International Association for Bridge and Structure Engineering Conference.Seoul：IABSE，2001：86－87.

［15］A daniel Ryszard，Frank J van Dooren，Rob H de Meijer.Comparison of a single and double main span suspension bridge for the western Scheldt crossing［C］／／34th International Symposium on Bridge and Structure Engineering：Venice：IABSE，2010：9－16.

［16］李国豪.桥梁结构稳定与振动［M］.北京：中国铁道出版社，1992.LI Guohao.Stability and vibration of bridge structures［M］.Beijing：China Railway Publishing House，1992.

［17］Gimsing N J.缆索承重桥梁——构思与设计［M］.金增洪，译.北京：人民交通出版社，2002.Gimsing N J.Cable supported bridges—concept and design［M］.Translated by JIN Zenghong.Beijing： China Communications Press，2002.

［18］熊文，孙斌，肖汝诚，等.CFRP与钢组合拉索斜拉桥经济性能分析［J］.哈尔滨工业大学学报，2011，43（8）：124.XIONG Wen，SUN Bin，XIAO Rucheng，et al.Economic behaviors of cable－stayed bridges with CFRP and steel composite stay cables［J］.Journal of Harbin Institute of Technology，2011，43（8）：124.