鞍形垫板加强T形相贯节点极限承载力分析

隋伟宁，陈以一，王占飞

（1.同济大学 土木工程防灾国家重点实验室，上海200092；2.沈阳建筑大学 土木工程学院，辽宁 沈阳110168）

相贯节点具有受力合理、外形简洁、加工制作方便和节约材料等优点，在工程中得到了广泛的应用.实际工程的桁架结构中，如果仅根据杆件截面强度去选择空心管材，而不考虑节点的承载力，可能会出现1个或几个节点承载力不能满足要求的情况.可以采用2种加强方法对节点进行加强以提高承载力：局部灌浆法和加强板法［1］.垫板加强型节点是利用加强板对节点承载力进行加强的方法之一，最初应用于海洋结构中防止节点发生冲击破坏.Fung，Choo等［2－4］的研究成果表明选择适当尺寸的加强垫板可以获得理想的加强效果.吴亮秦等［5］的实验研究成果表明对于垫板加强N形节点在一定范围内增加垫板厚度对提高节点极限承载力有效，而再增加垫板厚度可能会对结构受力不利.虽然垫板加强型节点是一种有效的提高节点极限承载力的方法，但是，国内外关于它的研究成果还很少.由于没有相关准则，Packer等［1］建议：将现行规范中相贯节点极限承载力设计的主管厚度由垫板厚度代替，作为垫板加强型节点的极限承载力设计公式.显然，这样得到的设计公式中未包含垫板与主管壁协同工作的影响，所以过于保守.为了方便垫板加强型节点的工程应用，有必要对它的力学性能进行研究.

目前，各国规范关于直接焊接相贯节点极限承载力公式都是以试验数据为依据建立起来的.现有的关于垫板加强型相贯节点的试验数据不多，仅根据这些试验数据无法全面把握节点的力学性能.有限元技术是目前应用较为广泛的模拟试验研究的方法之一，本文利用有限元分析软件Abaqus对垫板加强T形相贯节点进行数值模拟，并在我国现行《钢结构设计规范》（GB50017—2003）直接焊接相贯节点极限承载力公式的基础上引入节点极限承载力提高系数参数φ（轴向拉力或压力作用下垫板加强型节点与直接焊接相贯节点的极限承载力有限元计算结果的比值）对垫板加强T形相贯节点极限承载力N进行评价.

1 研究方法和分析模型

1.1 基本方法

影响N的可能因素有：垫板长度参数Δ，垫板宽度参数α，垫板厚度参数λ，主管半径厚度比γ，主支管直径比β等，其中，Δ＝δ／d，δ为垫板长度（垫板外边缘到支管外壁），d为支管的直径；λ＝tP／T，tP为垫板厚度，T为主管厚度；γ＝D／2T，D为主管的直径；β＝d／D.参见图1，图中，H为支管长度，t为支管厚度.首先进行单参数分析，考察该参数是否是影响N的主要参数.在确定影响N的主要参数的基础上通过多元回归的方法确定N的评价公式.

1.2 计算模型和边界条件

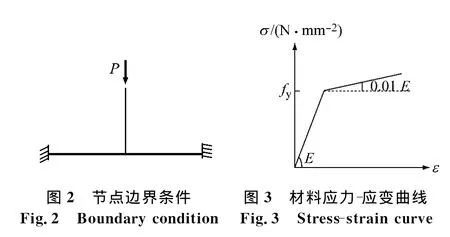
图1为垫板加强T形相贯节点的几何要素，其中，主管直径和主管长度在分析过程中保持不变，分别为245和1 500mm；支管长度取支管直径的5倍；当给定1.1节中的影响参数后，节点的其他几何尺寸就被唯一确定.采用的节点分析模型的边界条件如图2，主管两端固定，经分析可知，主管因变形产生的拉力对极限承载力的影响很小，支管末端为自由端，在支管末端施加轴向拉力或压力P作用.

图1 节点理论模型Fig.1 Theoretical model

1.3 材料性能

分析中假定钢材为Q345，其弹性模量E＝2.06×105N·mm－2，泊松比υ＝0.3，钢材屈服承载强度fy＝345N·mm－2.采用双线性材料本构关系，假定材料屈服后的弹性模量为初期弹性模量0.01倍，如图3所示，图中，σ为钢材应力；ε为钢材应变.材料遵守Von－Mises屈服准则及相关的流动法则.在建模分析时不考虑节点区焊缝以及焊接残余应力对钢管节点受压极限承载力的影响.

1.4 有限元单元类型

采用有限元分析软件Abaqus单元库中的S4R单元来模拟支管和主管；垫板及与垫板面积相同的主管管壁采用C3D8R实体单元.由于只有垫板边缘与主管壁之间焊接，所以分析模型中垫板边缘与主管壁采用tie连接，垫板表面与主管管壁采用接触边界条件.这样设置可以有效模拟在支管轴向压力作用下主管管壁随着垫板的变形而变形且不穿透、在支管轴向拉力的作用下垫板与主管发生脱离的现象，如图4a，4b，同时又能高效地完成模型的分析.

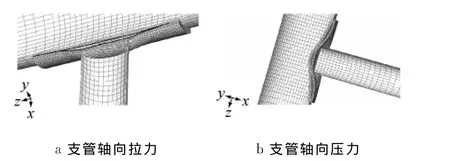
图4 支管轴向拉力和压力作用下的变形Fig.4 Deformation of the T－joints under brace tension and compression loading

1.5 分析模型与试验模型的比较

为了更好地把握有限元模型的准确性，利用上述有限元单元类型和边界条件，对Chiew等［7］的实验进行了有限元模拟，有限元模型的边界条件等与实验相同，单元的选取与前述内容相同，截面尺寸为：主管457.20mm×9.20mm；支管168.30mm×7.10mm；垫板457.20mm×457.20mm×9.60 mm.计算结果如图5所示.从图中可以看出有限元分析结果与实验结果吻合较好.

图6为实验节点变形图和有限元分析结果的变形图之间的关系，从变形图可以看出，有限元分析结果较好地模拟了实验的变形情况.

1.6 节点极限承载力和变形

采用弧长法求出各个节点模型的荷载－位移曲线，对于荷载－位移曲线没有出现荷载峰值的节点，其极限承载力根据Yura准则［7］确定，采用主管塑性变形达到0.03D时对应的荷载作为极限承载力.对于荷载－位移曲线出现荷载峰值的节点，如果荷载峰值出现在根据Yura准则判断的极限承载力之前，那么荷载－位移曲线的峰值作为节点的极限承载力；反之，用Yura准则确定极限承载力.

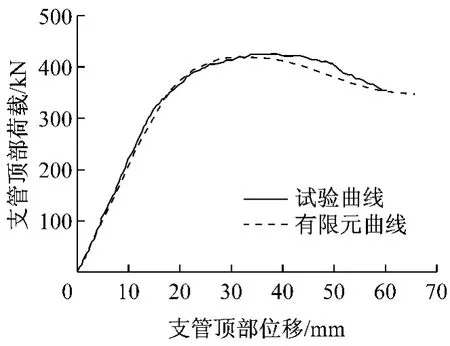
图5 荷载－位移曲线Fig.5 Load－deformation curves

图6 支管轴向压力作用下节点变形比较Fig.6 Comparison of experiment and FEA deformation result under compressive loading

在评价该类加强节点承载能力时，以腹杆轴向力P和弦杆相对凸凹变形δ的曲线为基础.其中相对凸凹变形δ为在轴力P作用下弦腹杆相贯面沿腹杆轴线方向的局部线位移（不包括弦杆作为梁弯曲时的挠度）.

2 计算结果与分析

2.1 确定参数Δ，α，λ中的主要影响参数

2.1.1Δ，α对节点极限承载力提高系数的影响

当参数λ＝1.0，β＝0.49，γ＝15.3时，Δ，α的变化对垫板加强T形相贯节点在轴向压力和拉力作用下的N及φ的影响情况如表1所示.NFEM为支管轴向拉力或压力的有限元计算结果.以α＝45.0°的计算结果为例，在支管轴向拉力作用下，Δ＝1.500d时φ最大值为1.2，Δ＝0.250d时φ最小值为0.9，其余均为1.1；在支管轴向压力作用下，除Δ＝0.250d时φ取得最小值1.0，其余均为1.5.可见，Δ较大时垫板长度的变化对φ的影响不明显.考虑焊接条件，建议加强垫板的长度参数Δ＝0.500d，且Δ≥50mm.

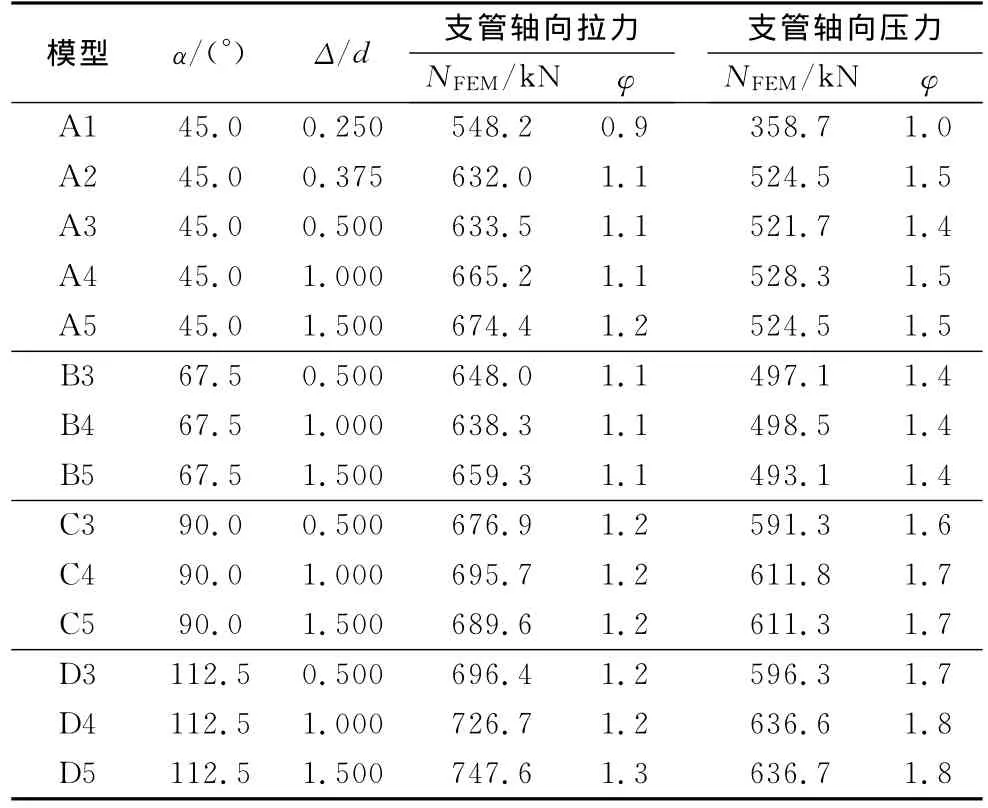
表1 参数Δ，α对φ的影响Tab.1 Effect of the parametersΔ，αon the parameterφ

以Δ＝0.500d时的计算结果为例，当α分别等于45.0°，67.5°，90.0°，112.5°时，在支管轴向拉力作用下φ分别为1.1，1.1，1.2，1.2，在支管轴向压力作用下φ分别为1.5，1.4，1.6，1.7，可见α的变化对φ略有影响.由于α的变化范围有限，另外考虑制作加工上的简便性，建议α＝90.0°.

2.1.2λ对节点极限承载力的影响

图7为Δ＝0.500d，α＝90.0°，β＝0.49，γ＝15.3，0.1≤λ≤4.0范围内时λ与N的关系.从图可见：①N随着垫板厚度的增加而呈增长趋势.② 在支管轴向压力作用下，随着λ的增加，N增加幅度逐渐减少，且有逐渐趋于定值的趋势.这是因为，在支管轴向压力作用下，随着垫板厚度的增加，由最初主管相对凸凹变形决定节点极限承载力变为由支管的承载能力决定N值.在支管轴向拉力作用下，N呈现稳步增长趋势，这是因为有限元模型中未考虑拉断的情况.当λ较大时，支管的拉伸量很大，远远超过了构件在轴向拉力作用下的变形能力.综上分析，λ是影响N的主要参数之一.

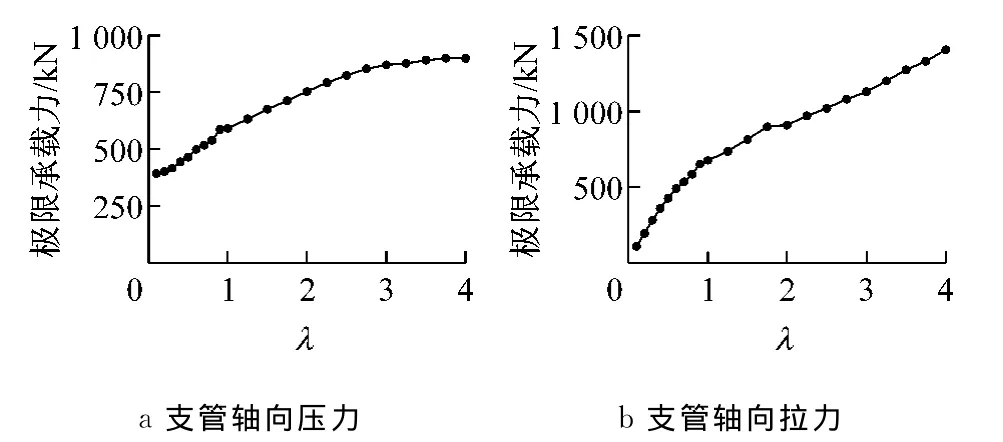
图7 λ对节点极限承载力的影响Fig.7 The effect of parameterλon the ultimate tensile and compressive loading

2.2 垫板加强型节点极限承载力评价公式

当α＝90.0°，Δ＝0.500d，λ为0.1～4.0时，分别取β＝0.25，0.49，0.70，γ＝10.2，15.3，30.0，50.0，通过将这几个参数进行任意组合，获得了205个有代表性的有限元模型，对这些模型进行有限元分析，所得到的分析结果如图8～10，可知：支管轴向拉力作用下的承载力评价公式中可以忽略参数γ和β的影响，只考虑参数λ的影响.支管轴向压力作用下的承载力评价公式中可以忽略参数γ的影响，只考虑参数β和λ的影响.

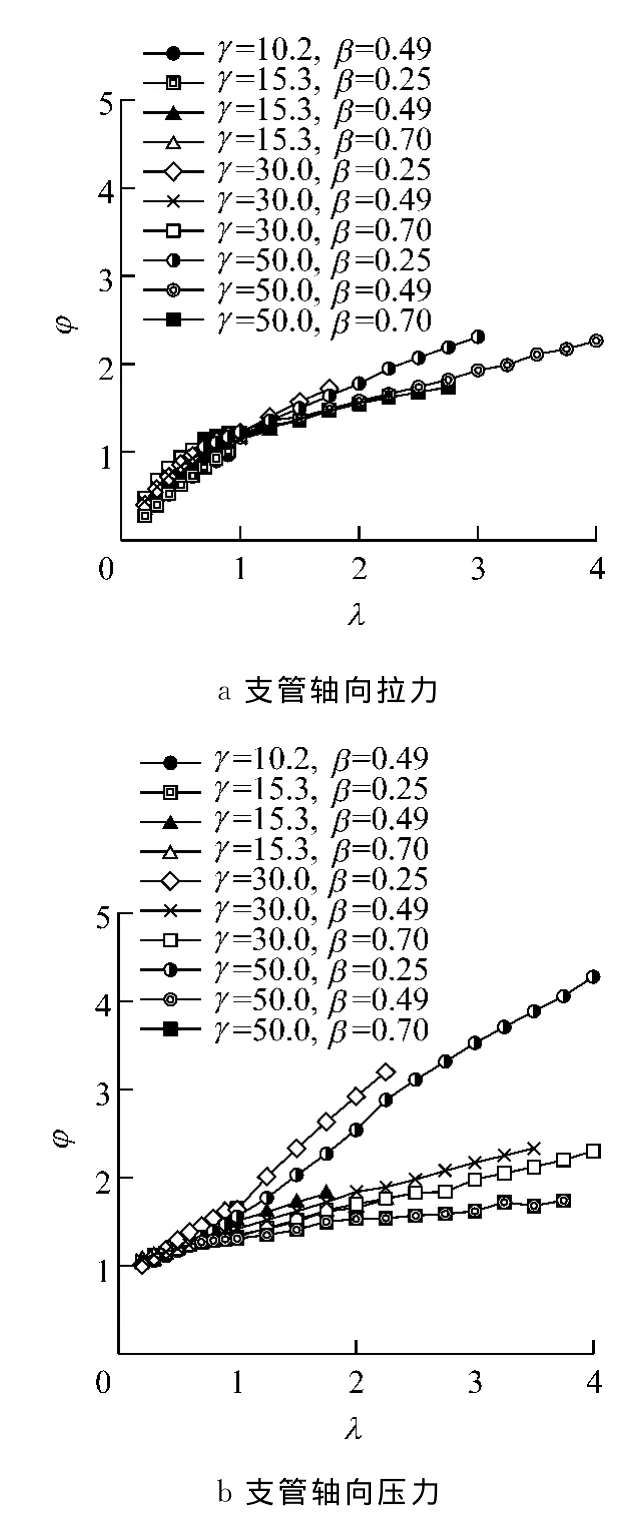
图8 λ对φ的影响Fig.8 Effect of parameterλon parameterφ

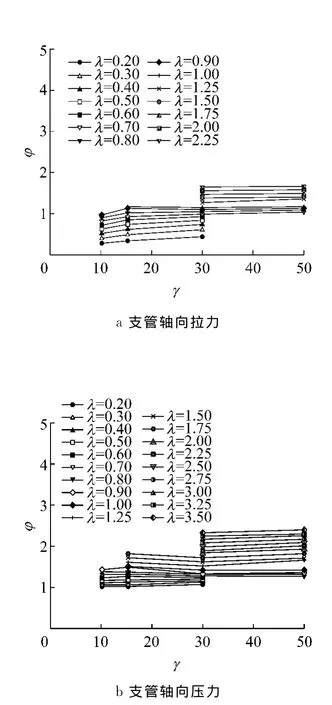
图9 β＝0.49时γ对φ的影响Fig.9 Effect of parameterγ on parameterφwhenβ＝0.49

图10 γ＝50.0时β对φ的影响Fig.10 Effect of parameterβ on parameterφwhenγ＝50.0

2.3 节点极限承载力系数评价公式

2.3.1 支管承受轴向拉力作用

由图7可知，在支管轴向拉力作用下φ随着λ的增加呈增长趋势，公式的数学模型定义为式（1）：

式中：φ′为极限承载力提高系数计算值；A为未知数；x1为参数.

该数学模型考虑了支管轴向拉力作用下当垫板厚度接近于零时N因为垫板丧失将支管上的荷载传递给主管的能力而趋近于零的情况.通过对有限元结果的回归分析，确定式（1）中的各个未知数，得到支管在轴向拉力作用下的φ′计算公式为

因此，在支管轴向拉力作用下，N的评价公式为

式中：NtT，Pj为现行《钢结构设计规范》（GB50017—2003）中直接焊接相贯节点受拉极限承载力.

2.3.2 支管承受轴向压力作用

在支管轴向压力作用下φ与量纲一化参数β，λ都相关.通过对所有有限元计算结果的回归分析，确定支管轴向压力作用下的φ′可按式（4）计算：公式考虑了当垫板厚度无限趋近于零时，垫板加强相贯节点应该与直接焊接相贯节点的极限承载力值相等的情况，即φ＝1.0的情况.因此，在支管轴向拉力作用下，N可用式（5）进行评价：

式中，NCT，Pj为现行《钢结构设计规范》（GB50017—2003）中直接焊接相贯节点受压极限承载力.

2.4 公式评价

图11a，11b分别为利用式（2）、式（4）计算得到的支管轴向拉力或压力作用下的φ′和有限元分析得到的φ之间的关系.图中的虚线为计算值与有限元值之间的误差求得的正态分布的95%的置信区间界限.分别对这2个公式求φ′／φ的平均值和协方差值，得到式（2）的平均值和协方差值分别为1.002和0.120，式（4）的平均值和协方差值分别为1.005和0.080.可见这2个公式可以很好地评价节点在支管轴向拉力或压力作用下的φ.

图11 φ的计算公式评价Fig.11 Evaluation of the design formulas for bearing capacity parameterφ

3 结论

（1）加强垫板的长度和宽度的变化对相贯节点支管轴向受拉和受压极限承载力的影响较小.考虑到制作方便和节约材料，建议Δ＝0.500d且不小于50mm，α＝90.0°.

（2）随着γ的增加N逐渐减少，但是γ对垫板加强型φ的影响很小.

（3）随着β的增加，N逐渐增加，β的变化对垫板加强型φ的影响情况为：在支管轴向压力作用下，随着β的增加φ逐渐减少；在支管轴向拉力作用下，β对φ的影响可以忽略.

（4）λ对N及φ的影响都很显著，变化规律为随着λ的增加节点的N和φ都呈增长趋势.但是，研究发现节点的极限承载力并非随着λ的增加一直处于增长状态，当参数λ过大时，由于决定节点极限承载力的破坏模态从主管壁的相对凸凹变形转变为支管在轴向压力作用下丧失承载能力，所以，N随着λ的增加而趋于某一定值.

（5）提出垫板加强T形相贯节点在支管轴向拉力和压力作用下的极限承载力评价公式.

［1］Packer J A， Henderson J E.Hollow structural section connections and trusses—a design guide［M］.2nd ed.Toronto：Canadian Institute of Steel Construction，1997.

［2］Fung T C，Chan T K，Soh C K.Ultimate capacity of doubler plate reinforced tubular joints［J］.Journal of Structural Engineering，1999，125（8）：891.

［3］Choo Y S，Van der vegte G J，Zettlemoyer N，et al.Static strength of T－joints reinforced with doubler or collar plates.I：experimental investigations ［J］.Journal of Structural Engineering，2005，131（1）：119.

［4］G J Van der Vegte，Choo Y S，Liang J X，et al.Static strength of T－joints reinforced with doubler or collar plates.II：numerical simulations［J］.Journal of Structural Engineering，2005，131（1）：129.

［5］吴亮秦，李自林，韩庆华.垫板加强N形圆钢管相贯节点静力性能试验研究［J］.建筑结构学报，2010，31（10）：83.WU Liangqin，LI Zilin，HAN Qinghua.Experimental study on static behavior of plate reinforced tubular N－joints［J］.Journal of Building Structures，2010，31（10）：83.

［6］Chiew S P，Soh C K，Fung T C.Large－scale testing of a multiplanar tubular DX－joint［C］.Proceeding 7thInternational Conference on Offshore Mechanics and Arctic Engineering 3.New York：ASME，1997：313－319.

［7］Yura J A，Zettlemoyer N，Edwards I F.Ultimate capacity of circular tubular joints［J］.Journal of the Structural Division，1981，107：1965.