有年龄生长模型应用于无年龄情况研究
邹奕巧,杜 群,葛宏立
(1.浙江农林大学 环境与资源学院,浙江省森林生态系统碳循环与固碳减排重点实验室,浙江 临安311300;2.浙江省森林资源监测中心,浙江 杭州 310020)
森林生长模型是指描述林木、林分或区域森林的某个或某几个变量甚至整个森林生态系统随时间推移而变化的过程的一类数学模型,如描述林木胸径、树高随时间变化的模型,描述林分平均胸径、平均树高、株数、直径分布状态随时间变化的模型等等。因为是描述随时间推移的变化过程,所以这类模型一般含有以显式或隐式方式存在的年龄因子。这类方程的形式很多,著名的有Richards模型[1-2],Schumacher模型[3],Schnute模型[4-5]等。这些模型有广泛应用,尤其涉及Richards模型的文献不计其数,直至目前仍被广泛应用,如模拟树高生长[6-7],优势高生长[8],断面积生长[9]等。如果年龄以显式的形式在模型中作为自变量出现,那么在建模和使用模型时必须测定林木或林分的年龄。直接使用年龄往往存2个方面问题:一是年龄测定困难。除了人工同龄林有档案可查外,一般天然林的年龄需要在野外测定。除了部分树种在树龄不大时可通过查数轮枝确定树龄(如马尾松Pinus massoniana),当树龄大了这个方法就失效,还有大部分针叶树具有较清晰的年轮,可通过生长锥确定树龄,但大面积使用或树木直径较大时,这种方法也不可行。而绝大部分阔叶树由于没有清晰的年轮,即使使用生长锥或伐倒,也难以确定树木的年龄。二是年龄并不一定有效。对于异龄林而言,林分的平均年龄意义并不大。即使异龄林中的林木个体,其年龄的意义也不是很大。根据孟宪宇等[10]对长白山云杉Picea koraiensis异龄林的研究,云杉林木胸径的生长过程并不是通常认为的S型曲线,而是拥有多个S型的曲线:当林木受压时生长缓慢,当附近有大树倒下或采伐时,光照条件改善生长加快,一定时间过后,上层树冠又变密,林木再次受压生长再次缓慢,这个受压—稀疏—受压的过程形成一个S型,而这样的受压—稀疏—受压过程在一株林木的一生中可能出现数次,最终造成胸径的生长曲线有多个S型。在这样的情况下,林木的真实年龄不但难以测定,而且意义也不大。由于这2个问题的存在,使得以年龄作为自变量的模型的建模和应用遇到困难,尤其是应用,因为在大规模应用时年龄测定几乎是不可能的,尽管年龄相对容易测定的树种,而在建模时可以花较大的成本采集年龄数据。已经有一些为了避免年龄问题的研究。如针对中国森林资源连续清查(以下简称CFI,continuous forest inventory)特点建立的年龄隐含的生长模型[11],它以Schumacher模型为原型,以2期复查样木数据为建模数据,并将模型应用于CFI数据的更新。再如年龄无关的优势高差分模型[12]。这些研究的共同特点是:首先假定一个模型,对于样本中的每个个体都有2次测定值,2次测定的时间间隔是已知的,根据第一个测定值计算一个理论年龄,将这个理论年龄值代入原模型,再加上时间间隔,这样在模型中消除了年龄这个变量。继而在这个模型的基础上估计模型参数。由于原始模型的因变量同时成了自变量,葛宏立[13]还针对这种模型的参数估计问题进行了探讨。这2个研究案例均针对国家CFI数据特点提出来,这样的清查体系中有大量定期测定的样木数据,但这些数据中缺少年龄数据。根据第7次全国森林资源清查结果[14],中国天然林面积占总面积的68%,蓄积占森林蓄积总量的86%,天然林占优势,而天然林的年龄测定始终是个问题。中国的CFI体系具有大量重复观测但无年龄的样木数据,研究将有年龄模型用于无年龄情况,可以为将已有的有年龄生长模型用于CFI数据的更新和预测做准备。所以继续研究针对CFI的避免年龄问题的模型应用依然具有积极的意义。本研究讨论的是不直接用CFI的数据建立年龄隐含的生长模型,而是讨论将通过其他途径建立的有年龄模型用于无年龄的CFI情况。在本研究中,用浙江省丽水市龙泉市的马尾松解析木数据建立有年龄胸径模型,然后用丽水市CFI的马尾松样木胸径数据进行有年龄模型无年龄应用试验。
1 材料与方法
1.1 研究区概况及数据
丽水市地处浙江省西南浙闽两省结合部,面积为1.73万km2,属亚热带季风气候,四季分明,温暖湿润,雨水充沛,无霜期长,具有明显的山地立体气候。年平均气温为18.3~11.5℃,平均年日照1 712~1 825 h。无霜期为180~280 d。年均降水量为1 400~2 275 mm。龙泉市为丽水市所辖县级市,面积为 0.31万 km2。
来自龙泉市9块标准地中的9株30年生以上的马尾松解析木数据用于有年龄胸径模型的建立,同时将它们分组,用于模型检验,每组数据由相邻的3个数组成。龙泉市199株马尾松解析木数据用于建立去皮胸径—带皮胸径转换模型。来自丽水市经1994,1999和2004年连续3次测定的1 614株马尾松固定样木数据用于模型在无年龄情况下的应用研究。
1.2 有年龄胸径模型的建立
根据9株解析木数据计算得到年龄及其所对应的胸径并计算平均胸径。由于树干解析得到的是去皮胸径,而实际应用时都是使用带皮胸径,因此,需要将去皮胸径转换成带皮胸径。利用龙泉市199株马尾松解析木的去皮胸径——带皮胸径数据建立转换模型:

式(1)中:D0为带皮胸径,Du为去皮胸径,换算后的平均胸径数据见表1。

表1 9株解析木年龄和平均胸径数据Table 1 Age and average DBH of 9 analytical trees
选择Richards模型作为有年龄马尾松胸径生长模型:

式(2)中:D为带皮胸径,A为年龄;m,c,r,k为待定系数。其中m为渐近线参数,表明平均胸径生长的极限值,参数c则决定了曲线和横轴即年龄轴的交点位置,因为胸径高度为1.3 m,所以曲线不经过原点,参数r决定了曲线的上升速度即胸径的生长速度,参数k则决定了曲线的S型的弯曲程度。Richards模型的每个参数都有生物学解释正是其广为应用的重要原因。用表1的数据采用非线性最小二乘法估计式(2)的参数,结果见表2。回归的剩余标准差S为0.119 6,决定系数R2为0.999 6。

表2 Richards胸径生长模型拟合结果Table 2 Fitting result of Richards DBH growth model
1.3 有年龄模型用于无年龄情况
采用单点估计法和双点估计法2种方法进行研究。单点估计法是根据前一期胸径数据估算理论年龄,再计算后期胸径理论值;双点估计法是根据前两期胸径数据以及调查的间隔期,算出理论年龄和理论生长指数,然后预测后期的胸径理论值。
1.3.1 单点估计法 设前期林木年龄和胸径数据为(Ad1,D1),后期为(Ad2=Ad1+△A,D2),△A为2次调查的间隔期,△A和D1已知,D2未知。根据(Ad1,D1)和式(2)可得:

代入式(2)有:

因为式(2)表示的是平均曲线,对于个体来说,有的在平均线之上,有的在平均线之下,有的甚至会大于渐近线。当D1大于渐近线m时,显然式(3)无解,这是正常现象。为了保证式(3)有解,对1 614株固定样木数据进行检验,剔除了超过渐近线的92株,剩下1 522株用于单点计算。由于9株解析木数据的胸径也是相邻的,所以也可以用于无年龄计算。先用公式将每株解析木的去皮胸径换算成带皮胸径,然后将非0的连续的每3个数据分为一组,记为D1,D2和D3,共有210组。考虑渐近线问题,剔除了9组,剩下201组。用固定样木计算时,取5或10,用1994年的数据估计1999年或用1999年的数据估计2004年的数据时取5,用1994年的数据估计2004年的数据时取10。用解析木数据计算时,取1或2,用D1估计D2或D2估计D3时取1,用D1估计D3时用2。结果见表4。
1.3.2 双点估计法 由于式(3)只描述了直径随年龄增长的平均变化关系,没有体现林木所处的立地质量、林木自身的竞争条件和遗传品质等因素。为考虑这些因素,引入生长指数IG(growth index),改进后的模型为:

无年龄情况的双点估计法是根据前2期调查的胸径数据算得理论年龄A和生长指数IG,再将理论年龄A加上调查间隔期ΔA以及生长指数IG算得第3期的理论胸径。假设第1期数据为(As1,D1),第2期数据为(As2=As1+ΔA,D2),则:

据式(6)(7)可解得:
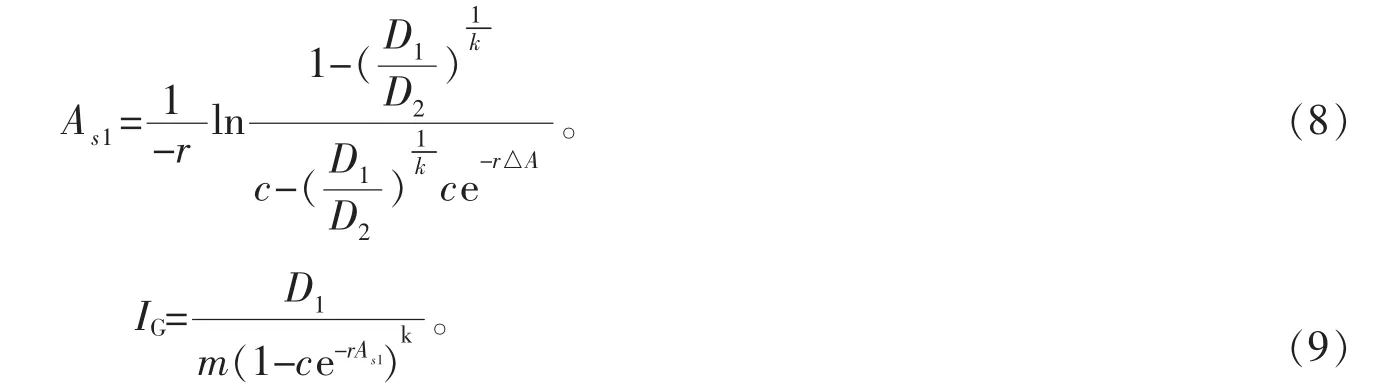
从而得到:

双点估计消除了渐近线问题,即使胸径大于渐近线也不妨害计算。计算结果见表5。
1.3.3 估计结果的评价本研究用以下几个指标进行评价
平均误差:

剩余标准差:

相关系数:

总相对误差百分数:

平均相对误差:

平均相对误差绝对值:

估计精度:

式(11)~(17)中:yi为实际值;i为估计值;n为样本数;ta为置信水平为a时的t分布值;为实际平均值,为估计平均值。
2 结果与分析
2.1 计算结果
因为解析木数据具有年龄,所以可以直接用式(2)来估计胸径,用9株解析木剔除胸径大于渐近线后的201组成对数据计算的结果见表3。

表3 直接用年龄计算的解析木胸径估计结果Table 3 Result of analytical tree data with age directly
用剔除胸径大于渐近线后的1 522株固定样木数据和201组解析木成对数据的单点估计结果见表4。
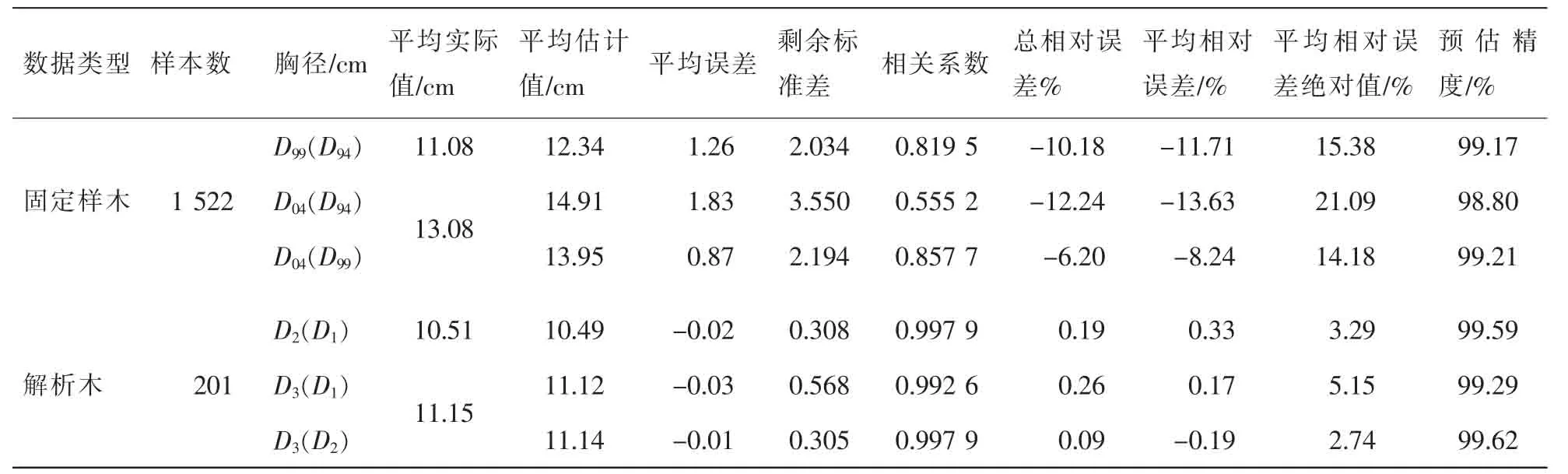
表4 单点估计法计算结果Table 4 Result of single point method
用全部1 614株固定样木数据和其中部分的1 522株数据,全部210组解析木成对数据及其中的201组数据用于双点估计,结果见表5。

表5 双点估计法计算结果Table 5 Results of double point method
2.2 结果分析
单点与双点的比较,双点的平均误差约是单点的1/2,其余各项指标也是双点有大幅提高。显然,双点的精度要比单点高。双点估计的总相对误差和平均相对误差的绝对值均小于4%,说明没有明显的系统偏差,这满足了一般的应用要求。但单点估计的总相对相差和平均相对误差大于10%。
用解析木数据计算的直接用年龄、单点和双点的比较,单点和双点的所有指标都比直接用年龄的要好很多,单点和双点比,双点比单点要好。
单点结果中,间隔期短的精度要比间隔期长的高。
图1为9株解析木不同方法估计的残差分析图,横坐标为序号,纵坐标为残差。从残差分布看,双点估计即 D3(D1D2)的残差最接近随机。单点估计 D2(D1),D3(D2),D3(D1)次之,直接用年龄的最差,说明对于不同的解析木存在明显的系统误差。
图2为固定样木数据不同方法估计的残差分析图。双点估计即D04(D94D99)具有最佳的残差分布,单点分布 D04(D99),D99(D94)次之,D04(D94)最差,与前面的分析一致。
3 结论与讨论
中国研制过很多有年龄生长模型,或是具备可以用于建立有年龄模型的以前调查的一些样地、样木数据。本研究有年龄模型是用丽水市的一个县内的少量解析木数据建立的,但用于整个丽水市的中国森林资源连续清查(CFI)数据的更新估计,且取得了满意的结果。本研究结果表明,有年龄生长模型是可以应用到无年龄但有重复测量数据的CFI数据的。这对利用中国大量CFI数据进行森林资源数据更新和预测具有积极的意义。
有年龄生长模型不但可以用于无年龄但有重复测量数据的情况,而且精度比直接用有年龄模型高。其中一个重要的原因是,无年龄情况下需要计算理论年龄,其实这个年龄不仅只有年龄的含义,同时含有立地质量、竞争因素、遗传因素等各种因素的综合作用,单点估计情况下是这样,双点估计情况下另增一个生长指数,更能体现个体的生长状况。当用前1个数据(单点)或前2个数据(双点)算得ΔA后,在更新或预测时可以用任意的ΔA值,这对更新和预测来说更加方便。
由于双点估计增加了一个生长指数,精度较高,同时适应性也更好,不存在直径大于渐近线时无法计算的问题。不利的方面是需要已知2个点。
单点估计只要已知一个点就可以进行更新估计,但精度较低,更不好处理的是当前期数值大于渐近线时无法估计的问题。本研究中剔除了胸径大于渐近线的数据,在实际工作中显然是不允许这么做的,因为这样做会造成估计数据的有偏。
[1] RICHARDS F J.A flexible growth function for empirical use [J].J Exp Bot,1959,10:290-300.
[2] CHAPMAN D G.Statistical problems in dynamics of exploited fisheries populations [C]//NEYMAN J.Proc 4th Berkeley Symp on Mathematics,Statistics and Probability(IV).Berkeley:University of California Press,1961:153-l 68.
[3] SCHUMACHER F X.A new growth curve and its application to timber yield studies [J].J For,1939,37:819-820.
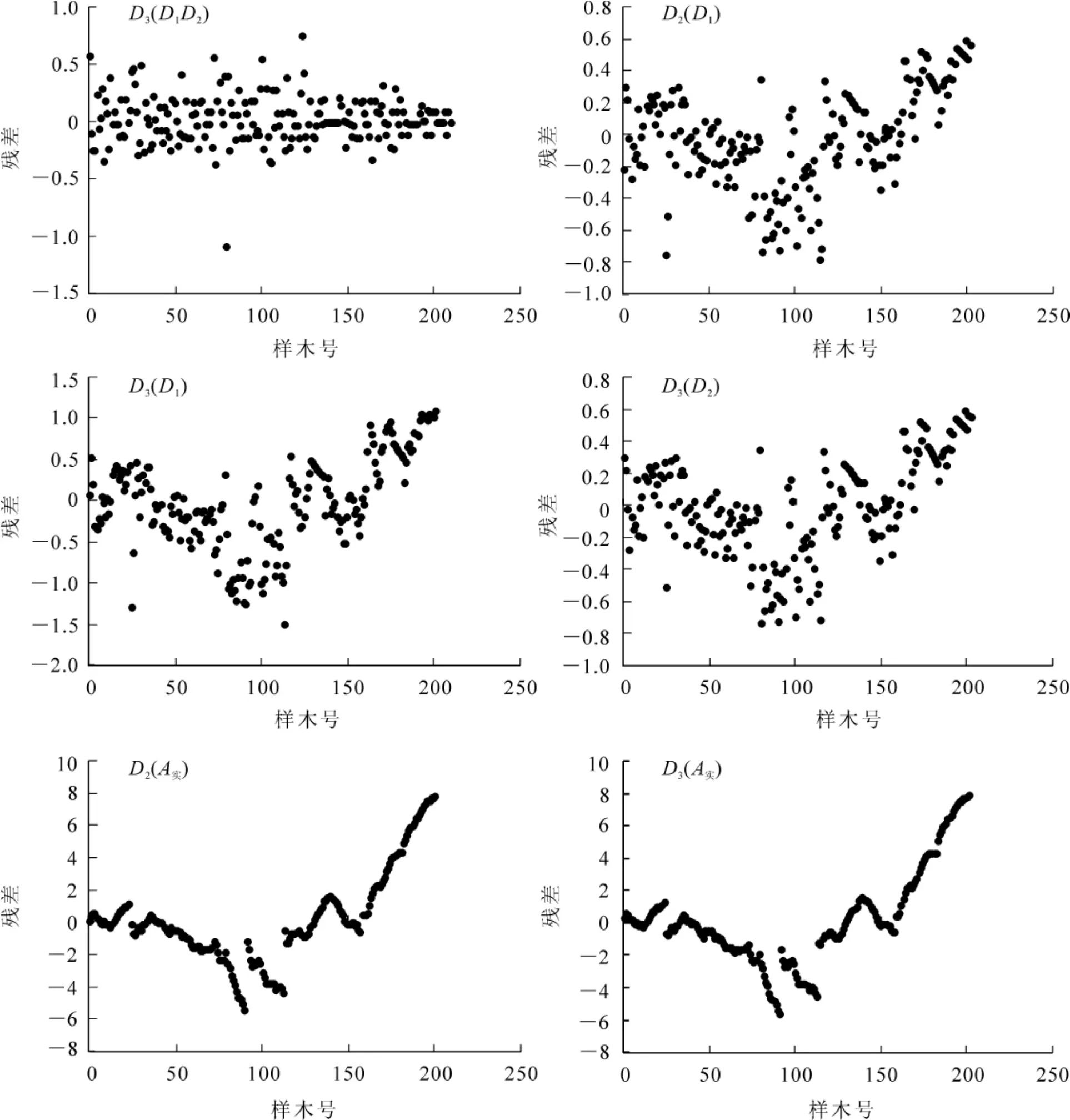
图1 9株解析木不同方法估计残差分析图Figure 1 Residual images with different methods of 9 analytical trees

图2 固定样本数据不同方法估计残差分析图Figure 2 Resiclual images with different methods of the permanent tree data
[4] SCHNUTE J.A versatile growth model with statistically stable parameters [J].Can J Fish Aquat Sci,1981,38:1128-1140.
[5] LEI Yuancai,MARQUES C P,MACEDO F W.Comparison of Schnute’s and Bertalanffy-Richards’ growth functions[J].For Ecol Manage,1997,96(3):283-288.
[6] BARTELINK H H.A growth model for mixed forest stands [J].For Ecol Manage,2000,134(1/3):29-43.
[7] PRETZSCH H,BIBER P,D^URSKY J.The single tree-based stand simulator SILVA:construction,application and evaluation [J].For Ecol Manage,2002,162(1):3-21.
[8] HUUSKONEN S,MIINA J.Stand-level growth models for young scots pine stands in Finland [J].For Ecol Manage,2007,241(1/3):49-61.
[9]唐守正,杜纪山.利用树冠竞争因子确定同龄间伐林分的断面积生长过程[J].林业科学,1999,35(6):35-41.TANG Shouzheng,DU Jishan.Determining basal area growth process of thinnined even aged stands by crown competition factor [J].Sci Silv Sin,1999,35(6):35-41.
[10]孟宪宇,葛宏立.云杉异龄林立地质量评价的数量指标探讨[J].北京林业大学学报,1995,17(1):1-9.MENG Xianyu,GE Hongli.A new quantitaive measure for evaluating site quality of unevenaged Picea stands [J].J Beijing For Univ,1995,17(1):1-9.
[11]葛宏立,项小强,何时珍,等.年龄隐含的生长模型在森林资源连续清查中的应用 [J].林业科学研究,1997,10(4):420-424.GE Hongli,XIANG Xiaoqiang,HE Shizhen,et al.Application of the age implicit growth model to continuous forest inventory [J].For Res,1997,10(4):420-424.
[12] TOME J,TOME M,BARREIRO S,et al.Age-independent difference equations for modelling tree and stand growth[J].Can J For Res,2006,36(7):1621-1630.
[13]葛宏立.自变量也含误差的非线性模型拟合[J].北京林业大学学报,1996,18(2):73-77.GE Hongli.Fitting of nonlinear models when independent variables are subject to error[J].J Beijing For Univ,1996,18(2):73-77.
[14] 国家林业局资源司.第 7 次全国森林资源清查结果[EB/OL].(2010-01-28)[2011-07-15].http://www.forestry.gov.cn/portal/main/s/65/content-326341.html.

