太阳电池最大功率及其跟踪模式

朱晓亮，程晓舫，张忠政

(中国科学技术大学 热科学和能源工程系，安徽 合肥230026)

0 引言

光伏电池的输出电压和输出电流随光照强度和电池结温的变化表现为强烈的非线性，但总是存在着一个唯一的最大功率输出(MPP)。为了在某个光照强度和电池结温下获得尽可能多的电能，就有一个最大功率跟踪(MPPT)的问题，以使得太阳电池尽量工作在最大功率点上。目前光伏发电系统的运行采用的最大功率点跟踪主要是优化策略较多的扰动观察法和电导增量法等［1］。

这些最大功率点的跟踪方式都是在未知最大功率点情况下通过一定的手段寻找到最大功率点，本文的创新点之一是通过最大功率方程和电流方程的联立求解，能得出最大功率点电压的表达式，从而确定最大功率点电流，直接通过计算得出最大功率点。由于得出的最大功率点电压的表达式是隐式表达式，计算过程需要迭代求解来完成。

目前最大功率点跟踪方面的研究主要在一个太阳光照强度下来进行。聚光条件下，能提供数个太阳光照强度，随着光照强度的增强，最大功率点轨迹会怎样变化，尚没有详细的分析研究。本文通过模拟得出随着光照强度增强以及减弱时最大功率点的全部变化轨迹，发现只要有串联内阻的存在，最大功率点随光照强度的变化轨迹在I－V坐标中总是呈现S形状。同时也确定了随着光照强度的变化最大功率点负载的变化范围。模拟得出的结果表明极强光照强度和极弱光照强度下最大功率点负载趋向于一个关于内阻的定值，因为实现最大功率点跟踪的实质就是调整负载，所以在最大功率点负载趋向定值时就无需调整，本文创新点之二既是提出了恒载跟踪。

由于太阳电池各模型参数，工作电压以及输出功率对温度的敏感度很大，而且在聚光情况下电池温度也会上升，为了方便考察聚光条件下最大功率点轨迹的变化规律，因此模拟中严格控制温度保持不变［2－3］。

1 最大功率方程

1.1 太阳电池电流方程

太阳电池外接负载RL后形成如图1所示的太阳电池电路模型图。

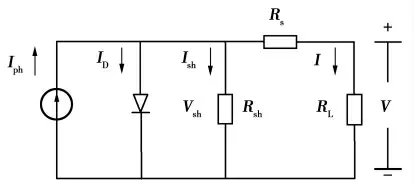
图1 太阳电池电路模型图

由固体物理理论及基尔霍夫定律推导得到太阳电池电流方程［4－5］

式中Iph——光生电流;

ID——二极管反向饱和电流;

n——二极管理想因子;

Rs——电池的串联内阻;

Rsh——电池的并联内阻;

Vth——温度电势，k，q=1.6×10－19C)。

对电流方程式(1)进行全微分并整理后得

1.2 温度不变下最大功率方程

为了考察电压和电流的变化关系，在光照强度变化的时候保持温度不变那么式(2)在某个温度环境中d ID=d ( nVth)=d Rs=d Rsh=0，电流和电压的改变( d I，d V)仅与光生电流的改变d Iph有关。

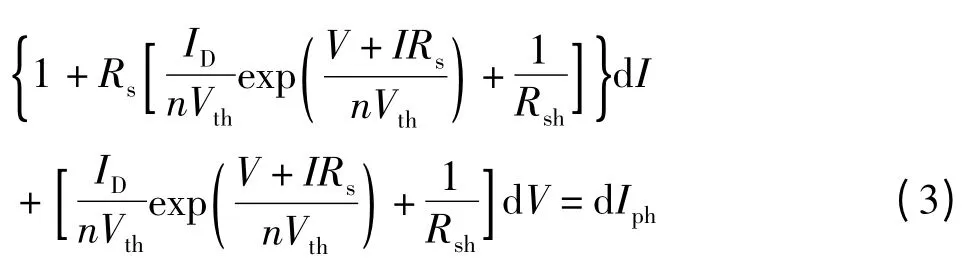
当光生电流的变化停止( d Iph=0)后，也就是在某一个光照强度下，希望输出功率能够落在极值功率Pm上。输出功率的描述为

令其全微分等于“0”

可以得到输出功率的极值条件

当光生电流不变，根据式(6)的输出功率极值条件，由式(3)就立即可以得到输出功率极值状态的数学描述为

我们将式(7)称之为最大功率方程，其表达了在d ID=d ( nVth)=d Rs=d Rsh=0时，某一光照下最大功率点电压和最大功率点电流应当符合的关系式，即当光照变化到某一值时，此时Vm和Im总是能够满足式(7)，于是可以在I－V图上绘制出最大功率点随光照强度变化的轨迹线。

2 全光照(光照强度从零到无穷大)下的最大功率轨迹及跟踪模式

2.1 全光照下最大功率轨迹线

根据欧姆定律，由式(7)可以得出在最大功率点上最大功率点负载的变化范围。

由式(8)，当Im→∞，Rm→Rs，当Im→0，Rm→Rs由太阳电池电流方程(1)，其中Im→∞对应着Iph→∞，亦即光照强度趋向无穷大，Im→0对应着Iph→0，亦即光照强度趋向0。可以得出最大功率负载的取值范围Rs＜Rm＜Rs+

选择由Charles等得到的某一硅太阳电池实验数据［6－8］，其模型参数为:二极管反向饱和电流ID=5.514×10－6A，串联电阻Rs=7.769×10－2Ω，并联电阻Rsh=25.9Ω，二极管理想因子n=1.727，温度电势得到T=306.1 K，现维持太阳电池工作温度随着光照强度变化保持不变，由式(7)在I－V图上绘制全光照下最大功率点的变化轨迹图2，曲线上的每一点显然都对应着一定光照强度下的一个最大功率点。

图2 全光照下最大功率点轨迹线

图2中曲线上限由于Rm→Rs，使得曲线无限接近于直线R=Rs。曲线的下限由于Rm→Rs+使得曲线无限接近直线R=Rs+，因为并联电阻Rsh较串联电阻Rs大很多，所以下限非常接近于横坐标I=0，如图3所示。

图3 图2局部放大

2.2 最大功率的三种跟踪模式

现将最大功率轨迹曲线由上到下分为五个小段，如图2所示。其中第一段①和第五段⑤是曲线分别非常接近的趋向两条直线R=Rs和R=Rs+，在这两个小段上，最大功率负载分别Rm→Rs和所以从最大功率跟踪的角度上来说，只需要将负载值固定在Rs和上，电池便工作在最大功率点上，无需进行最大功率点跟踪，称之为恒载跟踪。

图2中曲线的第三段③最大功率点电流不断增大但是最大功率点电压变化很小，可以近似的使用恒电压跟踪的情况，即CVT(Constant Voltage Tracking)［9］。

图2中曲线的第二段②和第四段④称之为过渡段。第四段是一个太阳光照强度下的情况，只有在聚光的时候才会有第二段的出现。

总结一下，太阳电池的最大功率跟踪，可以分为三种模式:

(a)恒载跟踪，适用于极强或极弱的光照状况;

(b)恒压跟踪，适用于中等强度的光照状况;

(c)计算跟踪，除上述光照状况的其它光照状况。

3 最大功率过渡段的计算跟踪

在曲线的第四段中是一个太阳光照下经常遇到的随着光照变化最大功率点变化差异较大的情况，目前已经有很多最大功率点跟踪的研究和技术，其中最常见的是扰动观察法和电导增量法。这些技术中都是未知最大功率点的情况通过一定技术寻找最大功率点或是尽量接近最大功率点。例如扰动观察法是周期性的给光伏电池的输出电压加扰动，比较其输出功率与前一周期的输出功率的大小。如果功率增加则在下一个周期以相同方向加扰动，否则改变扰动的方向，直到在最大功率点附近很小的一个阈值范围内。电导增量法是依据光伏电池的P－V曲线表现为单峰形状，在最大功率点必定有d P/d U=0，通过一定的调节步长判断d P/d U的符号使得在d P/d U≈0很小的范围内寻找到最大功率点［1］。本文提出过渡段的计算跟踪是利用式(5)的最大功率方程与式(1)的太阳电池电流方程联立求解，求得准确的最大功率点电压。

采用由Charles等得到的实验数据［8］，由式(7)和式(1)在I－V图上绘制图4。

图4 I－V图中一个太阳光照下最大功率点轨迹线

图4中点a是太阳电池当前的工作点，而最大功率点在点b，现通过最大功率方程与电流方程的联立求解，推导出最大功率点电压的隐式表达式，并由已知点a的电压和电流和太阳电池各模型参数代入表达式中即可迭代求解出最大功率点电压的值。

对于在最大功率点b上，由式(1)，

在点a上和最大功率点b两点上光生电流都是Iph。

由式(10)，在太阳电池模型参数Rs、Rsh、ID、n及太阳电池工作温度T为定值的情况下并读出当前工作点的电压电流值(V1，I1)，即可计算得出Iph的大小。

由于太阳电池电流方程(1)式中的电流I无法显式的用电压V来表示，反之亦然，为了方便联立求解，采用由LambertW函数构建的I－V电流方程的显式方程。式(1)的显式表达式［10］，

显式表达式在b点上，

将式(12)代入式(7)，得到式(13)，

在某个光照下，若太阳电池的所有模型参数Rs、Rsh、ID、n及太阳电池工作温度T都已知，测得太阳电池当前工作点的电压电流值(V1，I1)，再通过式(13)将最大功率点电压值Vm迭代计算出来，代入式(12)中即可计算Im的大小，这样就可以让太阳电池工作在准确的最大功率点上。

4 算例

由Charles等得到的实验数据［8］中，在光生电流Iph=0.561 A时 ，最大功率点电压Vm=0.390 V和最大功率点电流Im=0.481 A。

由于Charles等的实验中已经给出了光生电流，将太阳电池模型参数:二极管反向饱和电流ID=5.514×10－6A，串联电阻Rs=7.769×10－2Ω，并联电阻Rsh=25.9 Ω，二极管理想因子n=1.727，及太阳电池工作温度T=306.1 K代入式(13)利用Matlab软件数值计算得出最大功率点电压和最大功率点电流计算值，分别为:Vm=0.387 V，误差0.77%;Im=0.487 A，误差1.25%。

5 结论

(1)本文由太阳电池电流方程及其全微分推导出最大功率方程，在全光照条件下，其轨迹在I－V坐标中呈现S形状，并确定最大功率点负载的取值范围为

(2)太阳电池的最大功率跟踪，可以分为三种模式:

(a)恒载跟踪，适用于极强或极弱的光照状况;

(b)恒压跟踪，适用于中等强度的光照状况;

(c)计算跟踪，除上述光照状况的其它光照状况。

(3)通过最大功率方程与电流方程的显式表达式的联立求解得出最大功率点电压表达式，将已知数值代入可以迭代求解出来，避免了以往在未知最大功率点的情况下的寻找过程。算例表明计算跟踪的误差在1%左右。

［1］周林，武剑，贾秋华，等.光伏阵列最大功率点跟踪控制方法综述［J］.高电压技术，2008，34(6):1145－1154.

［2］黄国华，施玉川，杨宏，等.常规太阳电池聚光特性实验［J］.太阳能学报，2006，27(1):19－22.

［3］丁金磊.太阳电池I－V方程显式求解原理［D］.合肥:中国科学技术大学，2007:53－75.

［4］H.S.Rauschenbach.Solar Cell Array Design Handbook［M］.Litton Educational Publishing Inc，1980，169－170.

［5］赵富鑫，魏彦章.太阳电池及其应用［M］.北京:国防工业出版社，1985，207－213.

［6］Amit Jain，Avinashi Kapoor.A new method to determine the diode ideality factor of real solar cell using Lambert W－function［J］.Solar Energy Materials＆Solar Cells，2005，85(1):391－396.

［7］Jinlei Ding，Rakesh Radhakrishnan.A new method to determine the optimum load of a real solar cell using the Lambert W－function［J］.Solar Energy Materials＆Solar Cells，2008，92(1):1566－1569.

［8］J.P.Charles，M.Abdelkrim，Y.H.Muoy et al.A practical method of analysis of the current－voltage characteristics of solar cells［J］.Solar Energy Materials＆Solar Cells，1981，4(1):169－173.

［9］余世杰，何慧若.光伏水泵系统中CVT及MPPT的控制比较［J］.太阳能学报，1998，19(4):1－6.

［10］丁金磊.太阳电池I－V方程显式求解原理［D］.合肥:中国科学技术大学，2007:15－28.